Parallel Compensation in Two stage amplifier

Posted on Edited on In

Parallel Compensation is also known as Lead Compensation, Pole-Zero Compensation

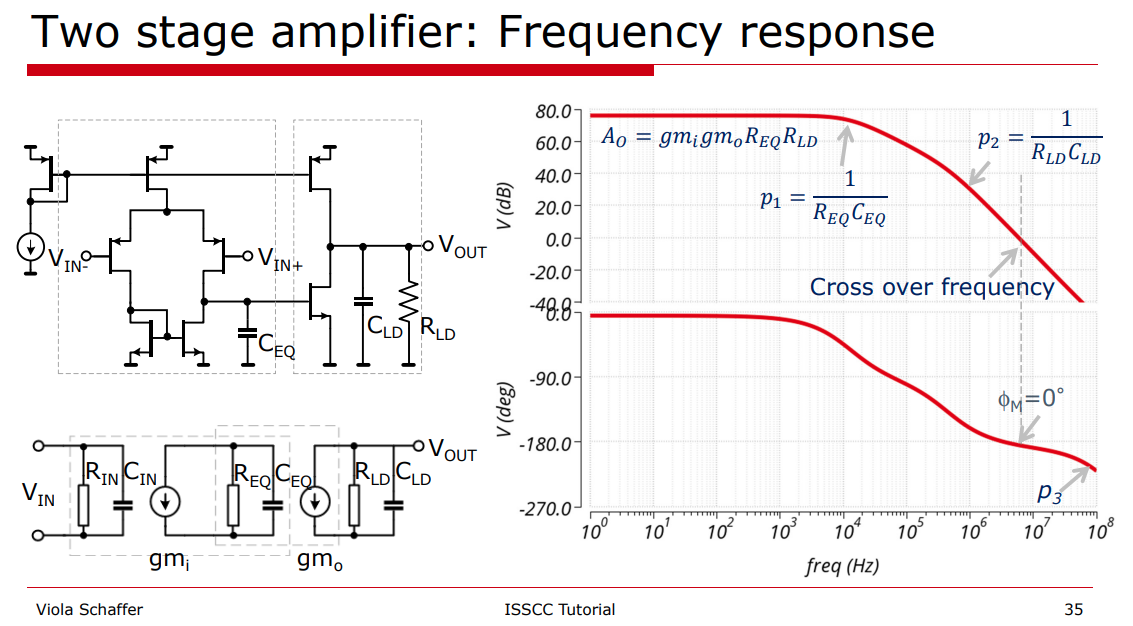
image-20220307234938855

Note: The dominant pole is at output of the first stage, i.e. \(\frac{1}{R_{EQ}C_{EQ}}\).

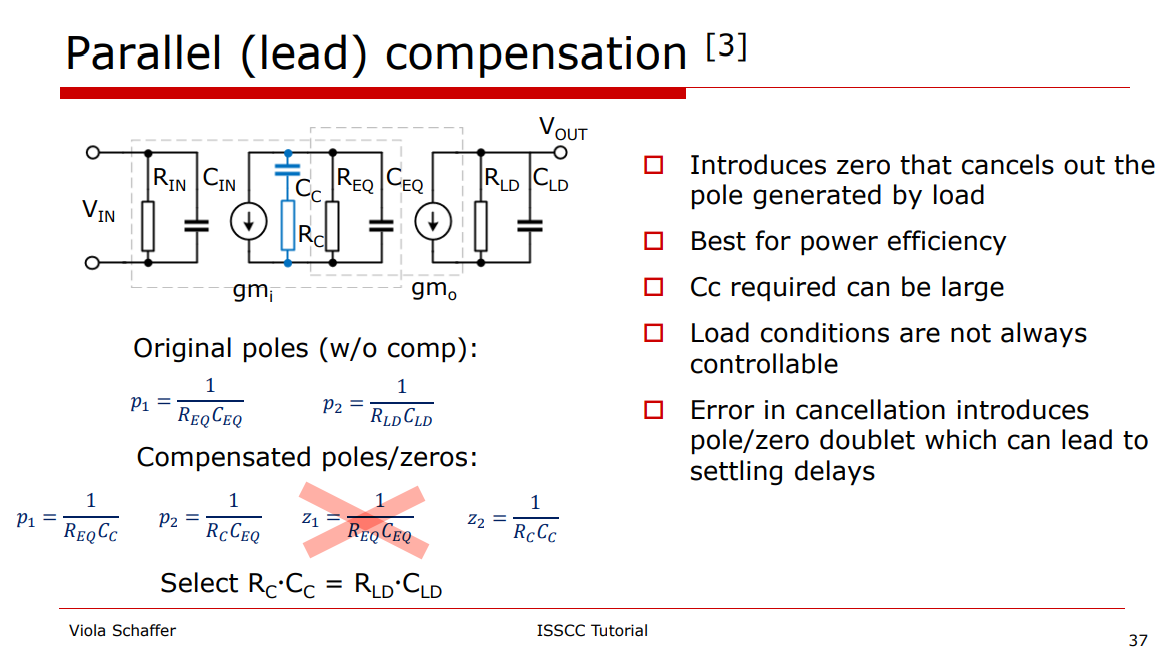
image-20221006001114562

Pole and Zero in transfer function

Design with operational amplifiers and analog integrated circuits / Sergio Franco, San Francisco State University. – Fourth edition

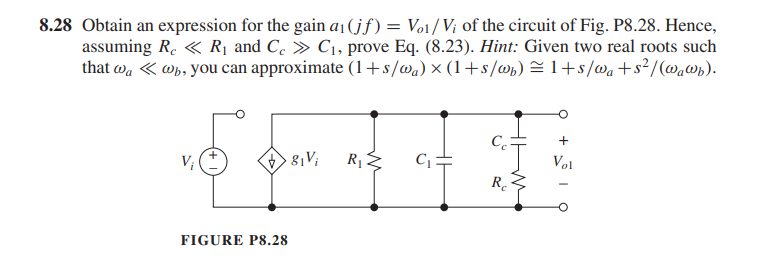
image-20221005220854411

\[ Y = \frac{1}{R_1} + sC_1+\frac{1}{R_c+1/SC_c} \]

\[\begin{align} Z &= \frac{1}{\frac{1}{R_1} + sC_1+\frac{1}{R_c+1/SC_c}} \\ &= \frac{R_1(1+sR_cC_c)}{s^2R_1C_1R_cC_c+s(R_1C_c+R_1C_1+R_cC_c)+1} \end{align}\] If \(p_{1c} \ll p_{3c}\), two real roots can be found \[\begin{align} p_{1c} &= \frac{1}{R_1C_c+R_1C_1+R_cC_c} \\ p_{3c} &= \frac{R_1C_c+R_1C_1+R_cC_c}{R_1C_1R_cC_c} \end{align}\]

The additional zero is \[ z_c = \frac{1}{R_cC_c} \] Given \(R_c \ll R\) and \(C_c \gg C\) \[\begin{align} p_{1c} &\simeq \frac{1}{R_1(C_c+C_1)} \simeq \frac{1}{R_1C_c}\\ p_{3c} &= \frac{1}{R_cC_1}+\frac{1}{R_cC_c}+\frac{1}{R_1C_1} \simeq \frac{1}{R_cC_1} \end{align}\]

The output pole is unchanged, which is \[ p_2 = \frac{1}{R_LC_L} \] We usually cancel \(p_2\) with \(z_c\), i.e. \[ R_cC_c=R_LC_L \]

Phase margin

unity-gain frequency \(\omega_t\) \[ \omega_t = A_\text{DC}\cdot P_{1c} =\frac{g_{m1}g_{m2}R_L}{C_c} \]

  1. PM=45\(^o\) \[ p_{3c} = \omega_t \] Then, \(C_c\) and \(R_c\) can be obtained

    \[\begin{align} R_c &= \sqrt{\frac{R_1}{C_1\cdot A_{DC}\cdot p_2}}=\sqrt{\frac{R_1\cdot R_LC_L}{C_1\cdot A_{DC}}} \\ C_c &= \sqrt{\frac{A_{DC}\cdot C_1}{R_1\cdot p_2}}=\sqrt{\frac{A_{DC}\cdot C_1 \cdot R_LC_L}{R_1}} \end{align}\]

  2. PM=60\(^o\) \[ p_{3c} = 2\cdot\omega_t \] Then, \(C_c\) and \(R_c\) can be obtained \[\begin{align} R_c &= \sqrt{\frac{R_1}{C_1\cdot 2A_{DC}\cdot p_2}} = \sqrt{\frac{R_1\cdot R_LC_L}{C_1\cdot 2A_{DC}}} \\ &= \sqrt{\frac{C_L}{2g_{m1}g_{m2}C_1}}\\ C_c &= \sqrt{\frac{2A_{DC}\cdot C_1}{R_1\cdot p_2}} = \sqrt{\frac{2A_{DC}\cdot C_1 \cdot R_LC_L}{R_1}} \\ &= R_L\sqrt{2g_{m1}g_{m2}C_1C_L} \end{align}\]

    for the unity-gain frequency \(\omega_t\) we find \[ \omega_t = \sqrt{\frac{1}{2}\cdot \frac{g_{m1}g_{m2}}{C_1C_L}} \] The parallel compensation shows a remarkably good result. The new 0 dB frequency lies only a factor \(\sqrt{2}\) lower than the theoretical maximum

To increase \(\phi_m\), we need to raise \(C_c\) a bit while lowering \(R_c\) in proportion in order to maintain pole-zero cancellation. This causes \(p_{1c}\) and \(p_{3c}\) to split a bit further apart.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
clc;
clear;

fd = 84*1e3;	% dominant freq, unit: Hz
fnd = 3.25*1e6;	% unit: Hz
C = 478*1e-15;
R = 1/fd/(2*pi)/C;
Adc = 10^(80/20);

ri = 2; % PM=45: 1;  PM=60: 2
Rc = (R/C/fnd/2/pi/ri/Adc)^0.5; % compensation resistor
Cc = (ri*Adc*C/fnd/2/pi/R)^0.5; % compensation capacitor

wzc = 1/2/pi/Rc/Cc; % zero frequency

reference

Viola Schäffer, Designing Amplifiers for Stability, ISSCC 2021 Tutorials

R.Eschauzier "Wide Bandwidth Low Power Operational Amplifiers", Delft University Press, 1994.

Gene F. Franklin, J. David Powell, and Abbas Emami-Naeini. 2018. Feedback Control of Dynamic Systems (8th Edition) (8th. ed.). Pearson. 6.7 Compensation

Application Note AN-1286 Compensation for the LM3478 Boost Controller

ECEN 607 Advanced Analog Circuit Design Techniques Spring 2017 URL: Lect 1D Op-Amps Stability and Frequency Compensation Techniques

Sergio Franco, San Francisco State University, Design with Operational Amplifiers and Analog Integrated Circuits, 4/e

J. H. Huijsing, 6.2.2.1 Two-GA-stage Parallel Compensation (PC), "Operational Amplifiers, Theory and Design, 3rd ed. New York: Springer, 2017"