jitter amplification

Posted on Edited on In

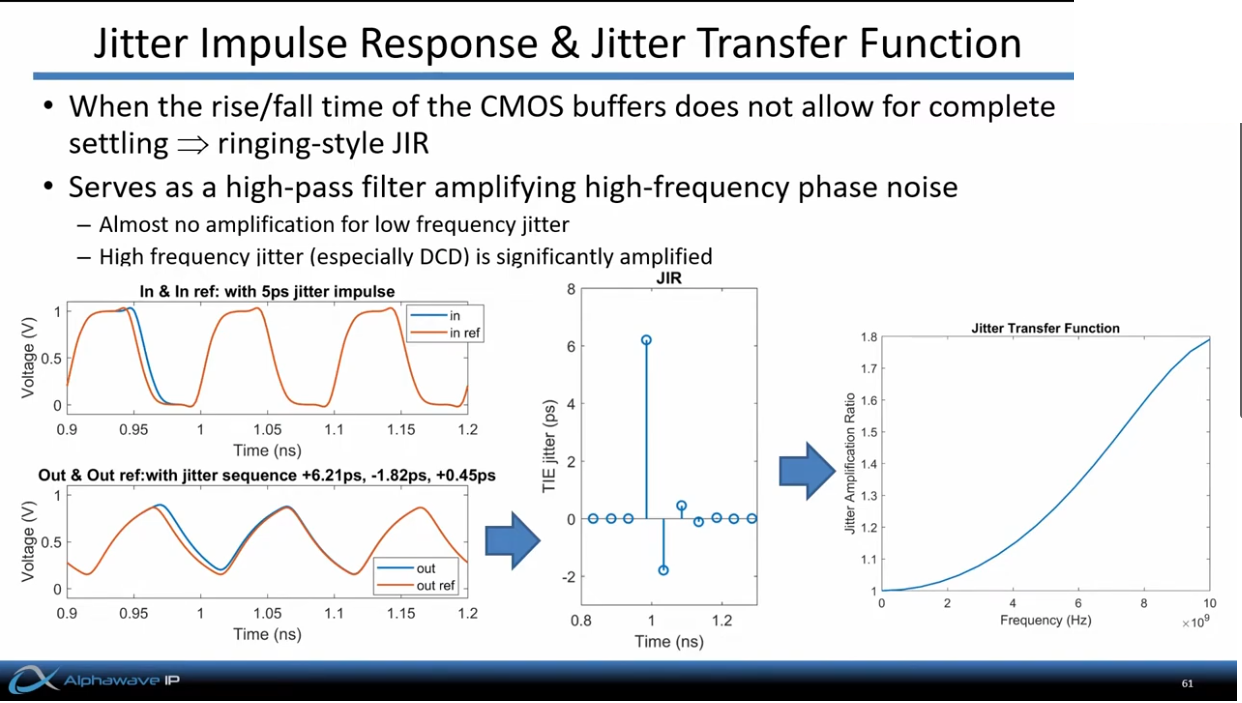
Jitter amplification arises from the transfer characteristic of the clock path, without considering other jitter sources, such as supply noise or thermal noise of the buffer

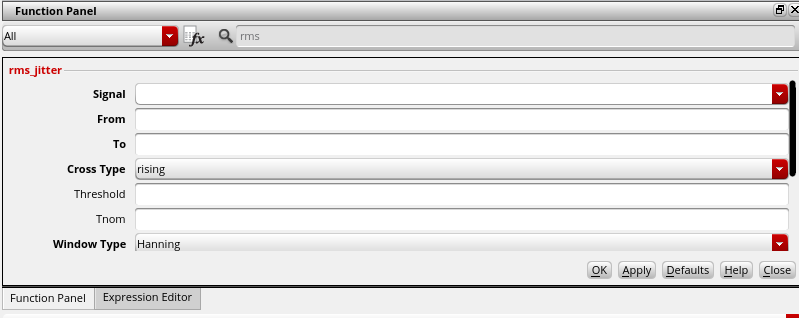
transient noise and rms_jitter function

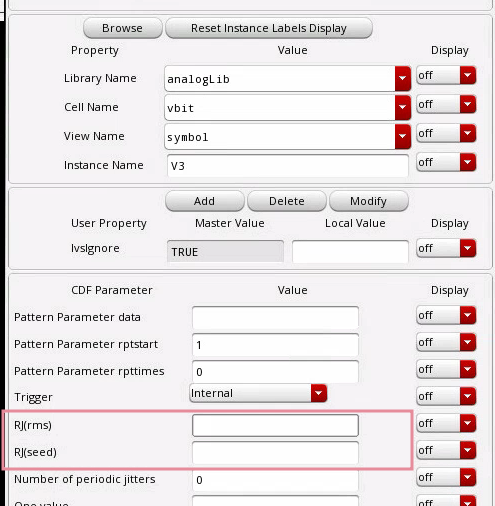
image-20220608233610066

image-20220313230930333

RJ(rms): single Edge or Both Edge?

RJ(seed): what is it?

phase noise method

Directly compare the input phase noise and output phase noise, the input waveform maybe is the PLL output or other clock distribution end point

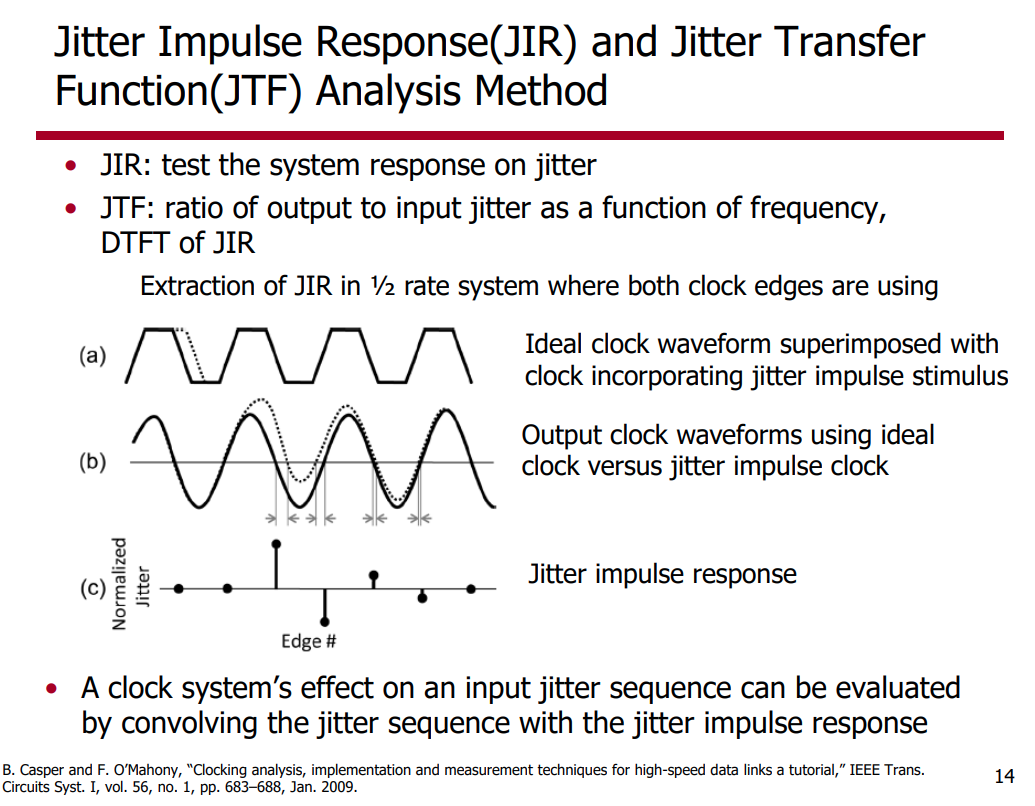
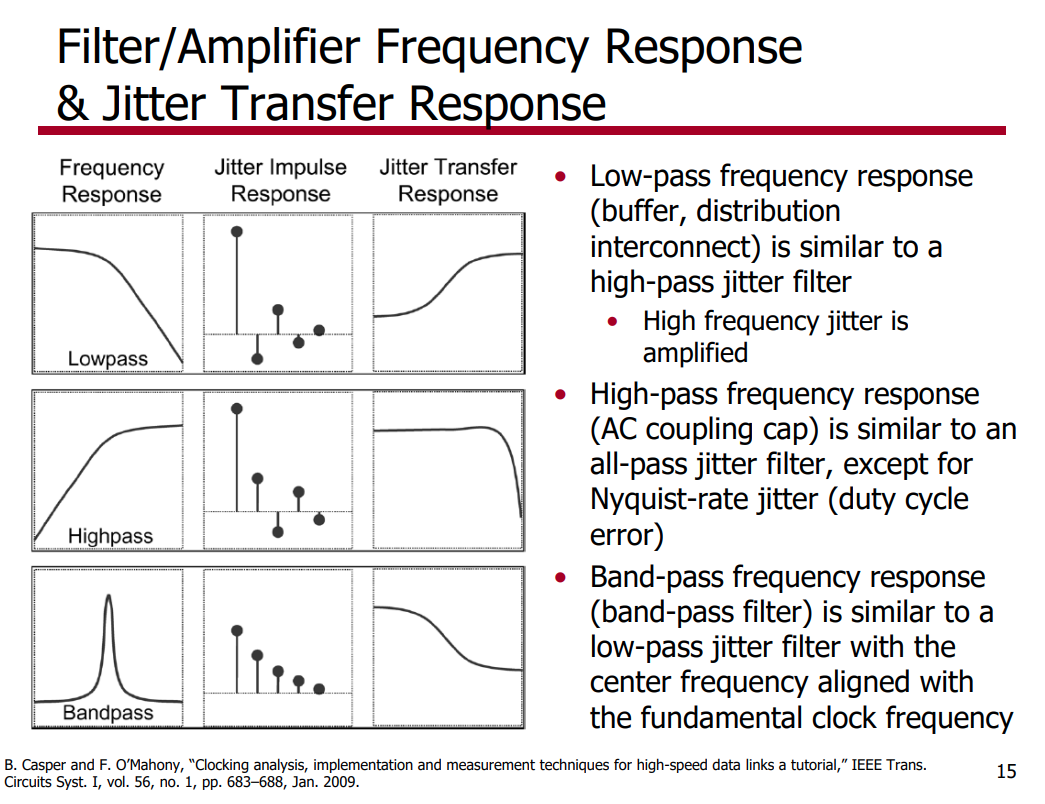
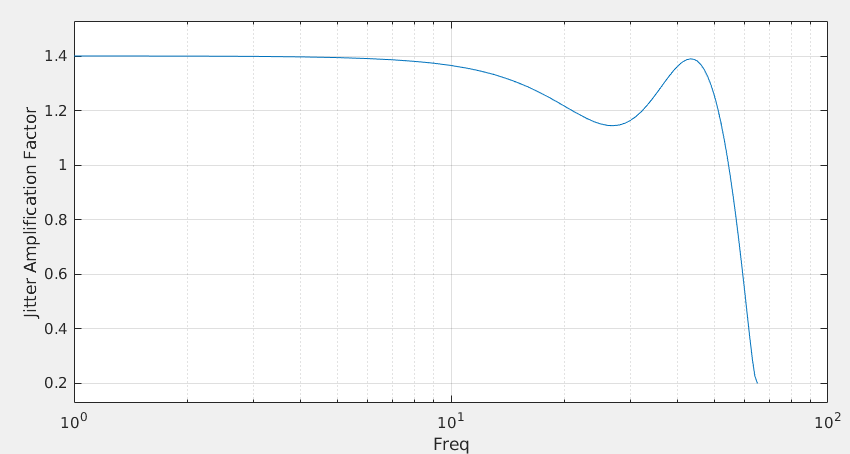
Jitter Impulse Response & Jitter Transfer Function

assuming linear, time-invariant phase response

image-20250522223530464

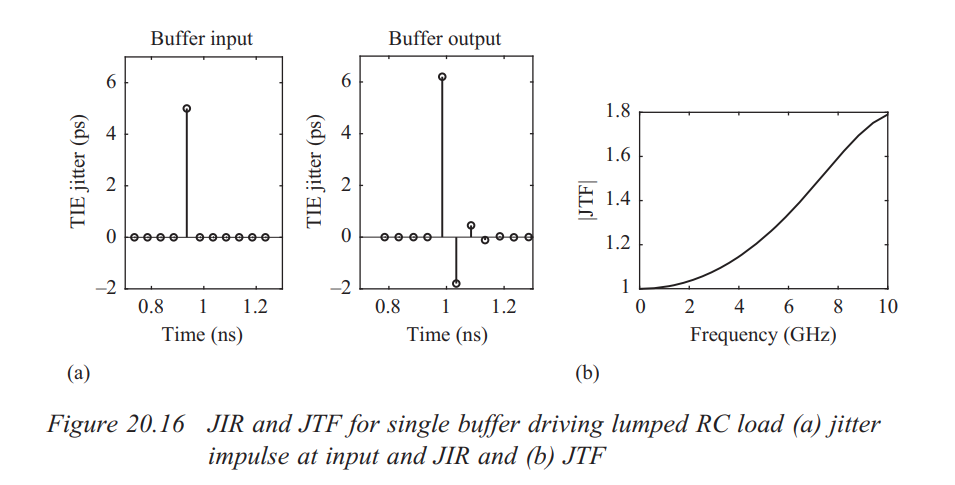
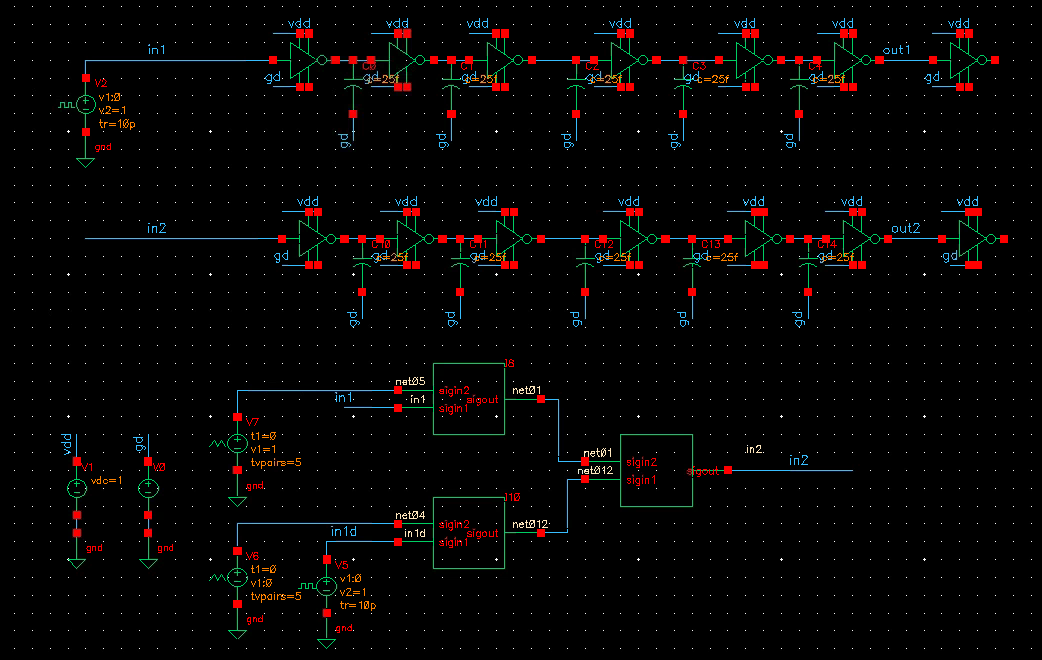
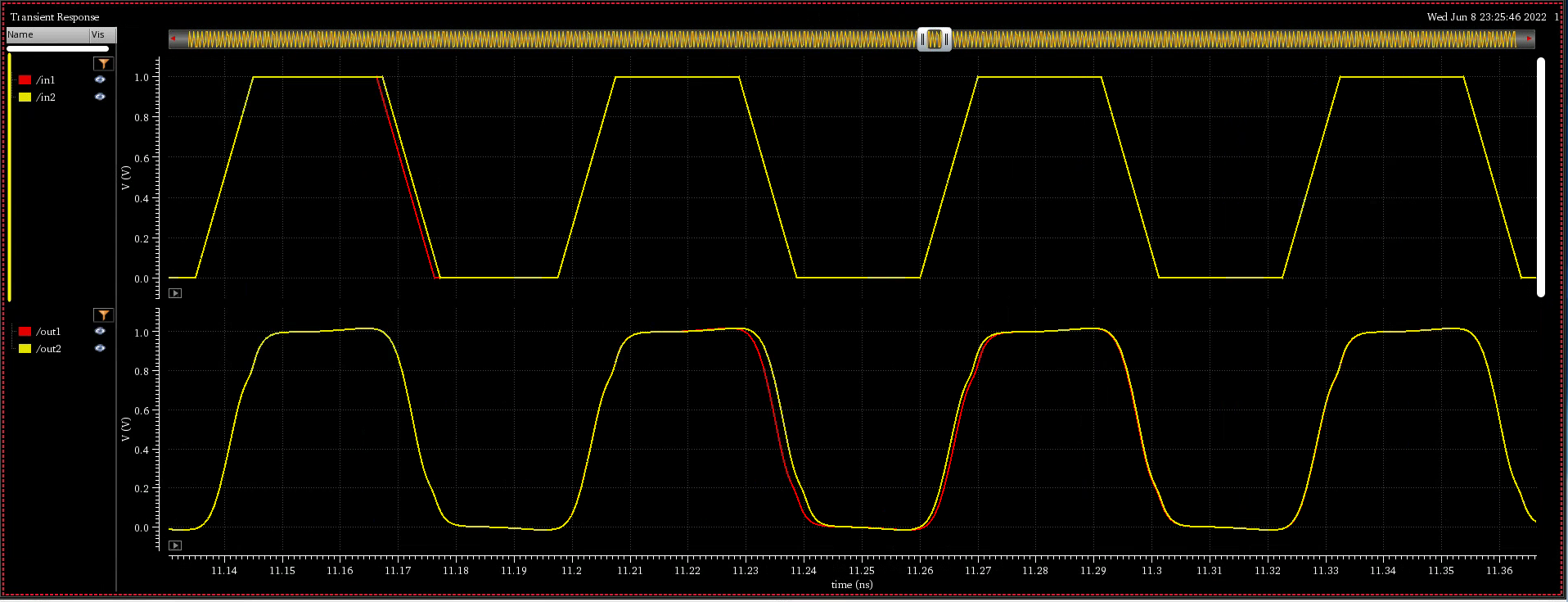
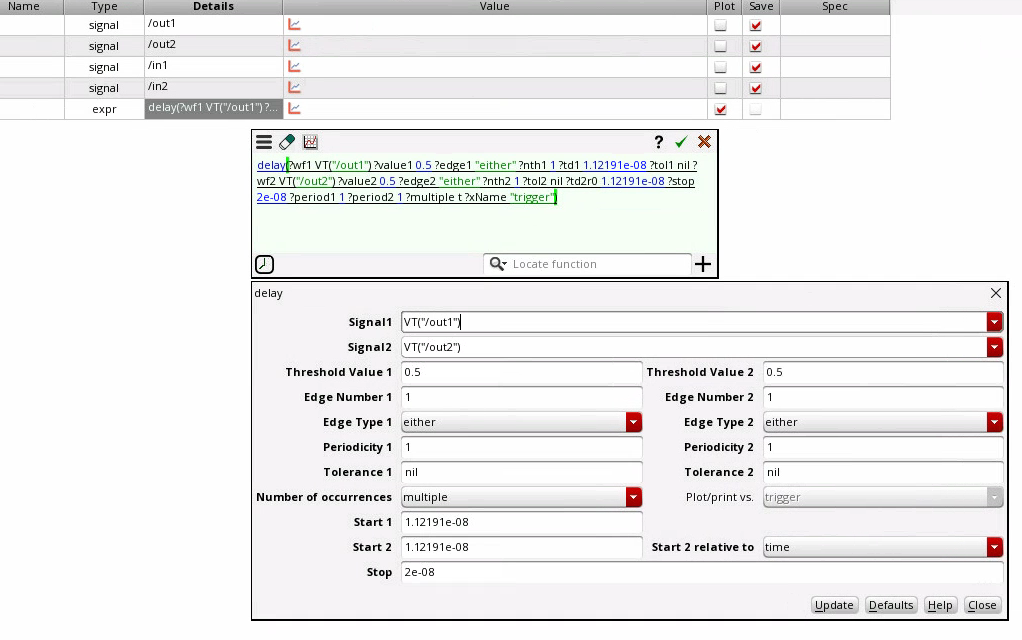
n =5 buffers, fclk = 10GHz

[Alphawave’s CTO, Tony Chan Carusone, High Speed Communications Part 8 – On Die CMOS Clock Distribution]

image-20220313231013645

image-20220313231027512

Example

Low Pass Filter

image-20220322124344158

1
2
3
4
5
6
7
8
9
10
11
N = 32;
x = zeros(N,1);
x(1) = 6;
x(2) = -2;
x(3) = 0.5;
x = x/5;
figure(1)
stem(x)
Y = fft(x, N);
figure(2)
plot(abs(Y(1:N/2)));

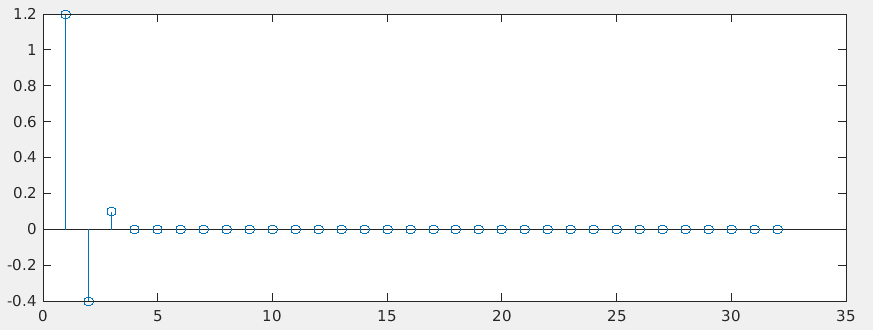
image-20220322124902394

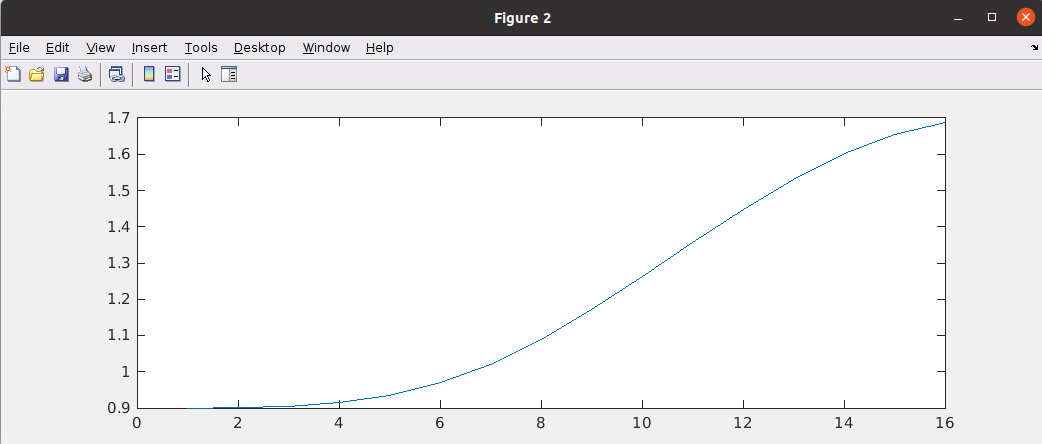
image-20220322124932584

discrete time jitter impulse response

both input and output are discrete time signal, i.e. no sampling in the input, that's why ratio \(1/T_s\) is not in the jtf

High Pass Filter

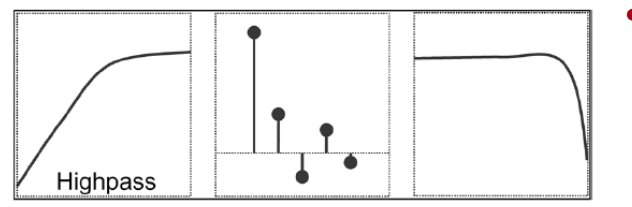
image-20220327010223664

1
2
3
4
5
6
7
8
9
10
11
12
N = 128;
j_hp = zeros(N, 1);
j_hp(1)= 1;
j_hp(2) = 0.5;
j_hp(3) = -0.3;
j_hp(4) = 0.3;
j_hp(5) = -0.1;
jtf_hp = abs(fft(j_hp));
semilogx(jtf_hp(1:N/2+1));
xlabel('Freq');
ylabel('Jitter Amplification Factor');
grid on;

image-20220327010421475

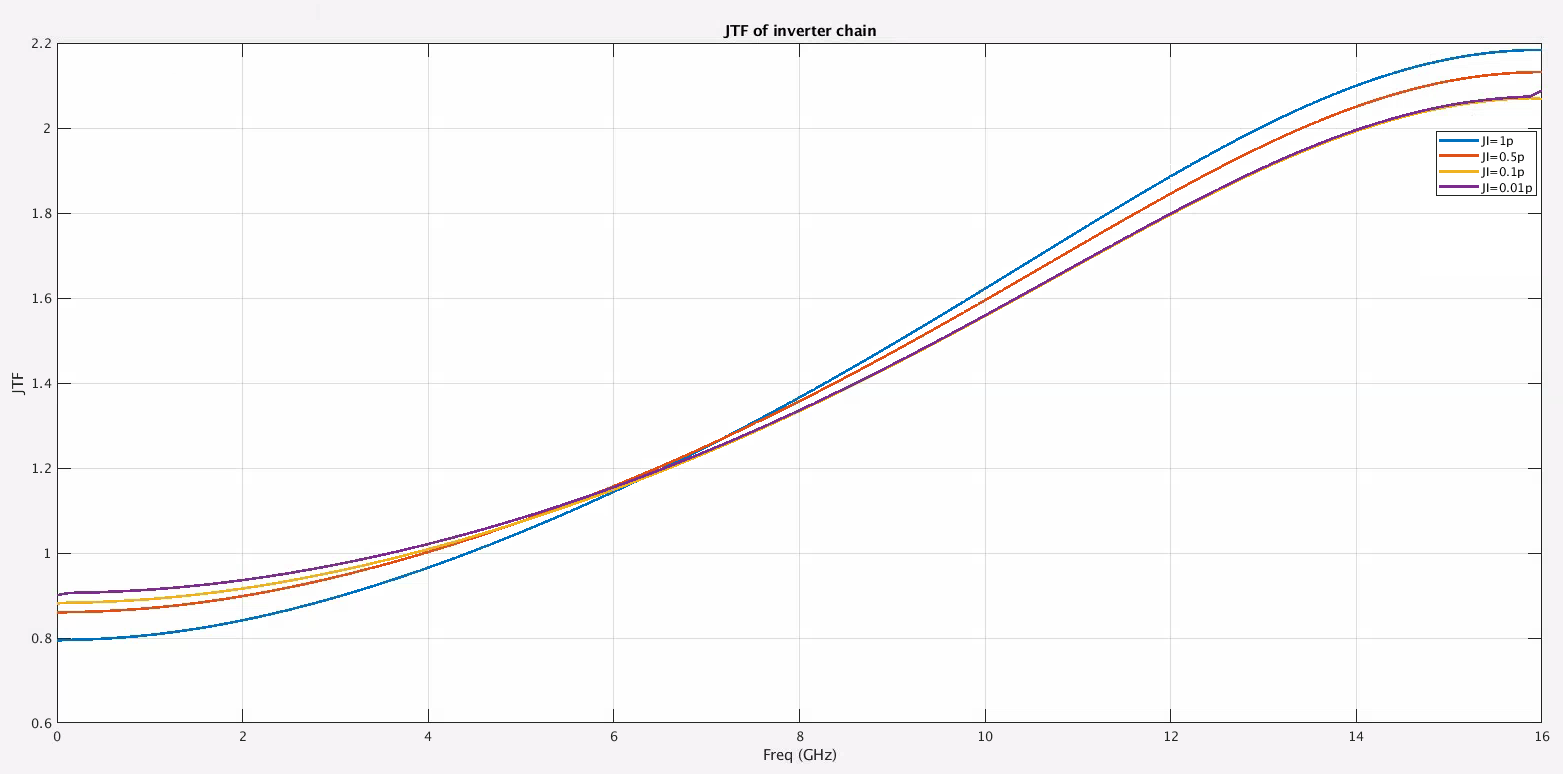
inverter chain

image-20220608232251056

image-20220608232658054

image-20220608232438188

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ji = 1e-12; % 1ps
data = importdata('/path/to/jir.csv');
jo = data.data(:, 2);
Ts = 31.25e-12;
Fs = 1/Ts;
jir = jo/ji;
N = 2^(nextpow2(length(jir)-1));
Y = fft(jir, N);
jtf = abs(Y(1:N/2+1));
freqs= Fs/N*(0:N/2);
plot(feqs/1e9, jtf, 'linewidth', 2);
grid on;
xlabel('Freq (GHz)');
ylabel('JTF');
title('JTF of inverter chain');

image-20220608233303576

Phase Noise Integration Limits

image-20250522225506217

[Alphawave’s CTO, Tony Chan Carusone, High Speed Communications Part 8 – On Die CMOS Clock Distribution]

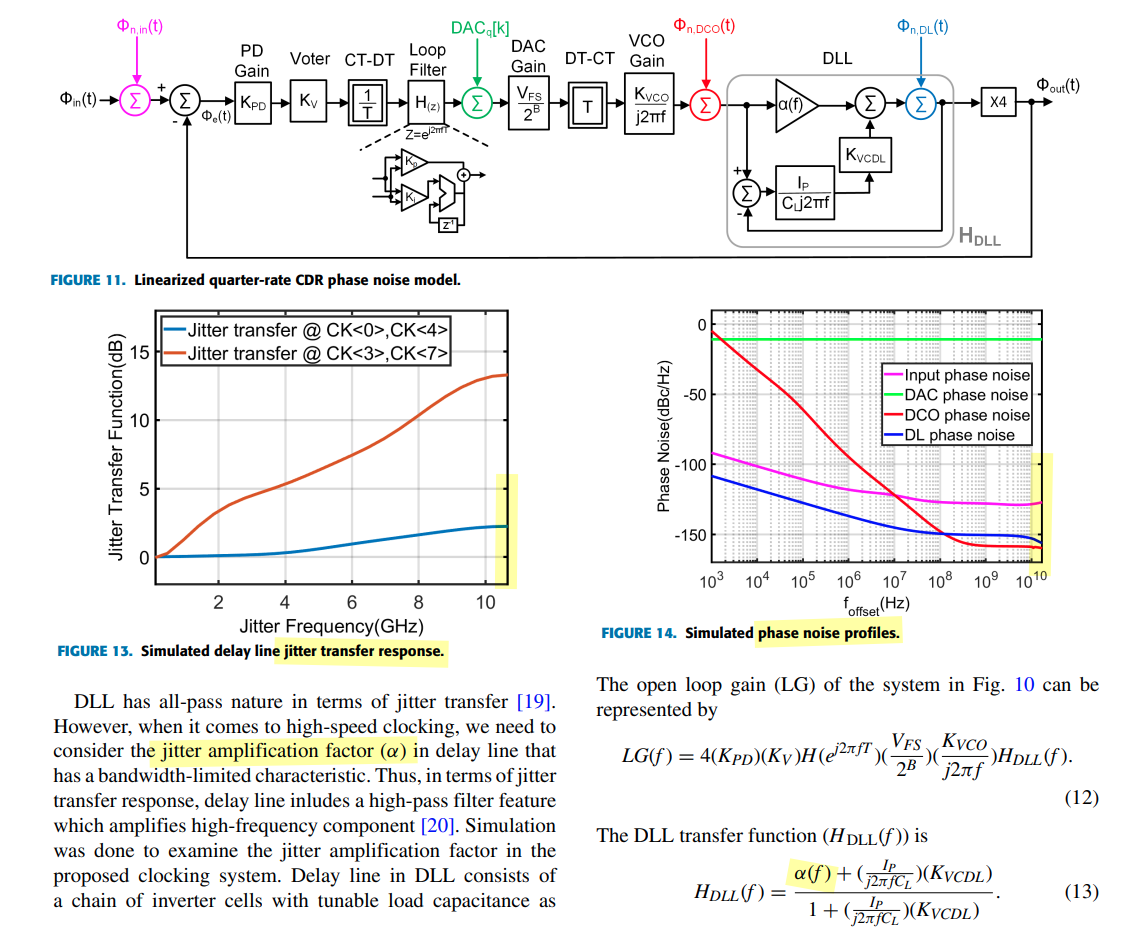
image-20250522234522208

Four major noise sources are included in the modeling: Input noise, DAC quantization noise (DAC QN), DCO random noise (DCO RN), and delay line random noise (DL RN).

H. Kang et al., "A 42.7Gb/s Optical Receiver with Digital CDR in 28nm CMOS," 2023 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), San Diego, CA, USA, 2023 [https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=10630516]

Reference

Sam Palermo, ECEN 720, Lecture 13 - Forwarded Clock Deskew Circuits

B. Casper and F. O'Mahony, "Clocking Analysis, Implementation and Measurement Techniques for High-Speed Data Links-A Tutorial," in IEEE Transactions on Circuits and Systems I. [https://people.engr.tamu.edu/spalermo/ecen689/clocking_analysis_hs_links_casper_tcas1_2009.pdf]

Phase-Locked Frequency Generation and Clocking : Architectures and Circuits for Modern Wireless and Wireline Systems by Woogeun Rhee (2020, Hardcover)

Mathuranathan Viswanathan, Digital Modulations using Matlab : Build Simulation Models from Scratch

Tony Chan Carusone, University of Toronto, Canada, 2022 CICC Educational Sessions "Architectural Considerations in 100+ Gbps Wireline Transceivers"

X. Mo, J. Wu, N. Wary and T. Chan Carusone, "Design Methodologies for Low-Jitter CMOS Clock Distribution," in IEEE Open Journal of the Solid-State Circuits Society, 2021 [https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9559395]

Modeling Oscillators with Arbitrary Phase Noise Profiles [https://community.cadence.com/cadence_blogs_8/b/rf/posts/modeling-oscillators-with-arbitrary-phase-noise-profiles]

Y. Zhao and B. Razavi, "Phase Noise Integration Limits for Jitter Calculation," 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 2022 [https://www.seas.ucla.edu/brweb/papers/Conferences/YZ_ISCAS_22.pdf]