Laplace Transform and z-Transform in System Analysis

Posted on Edited on In

The Laplace transform converts integro-differential equations into algebraic equations - continuous-time systems

The z-transforms changes difference equations into algebraic equations - discrete-time systems

FIR Equalization

Frequency Response

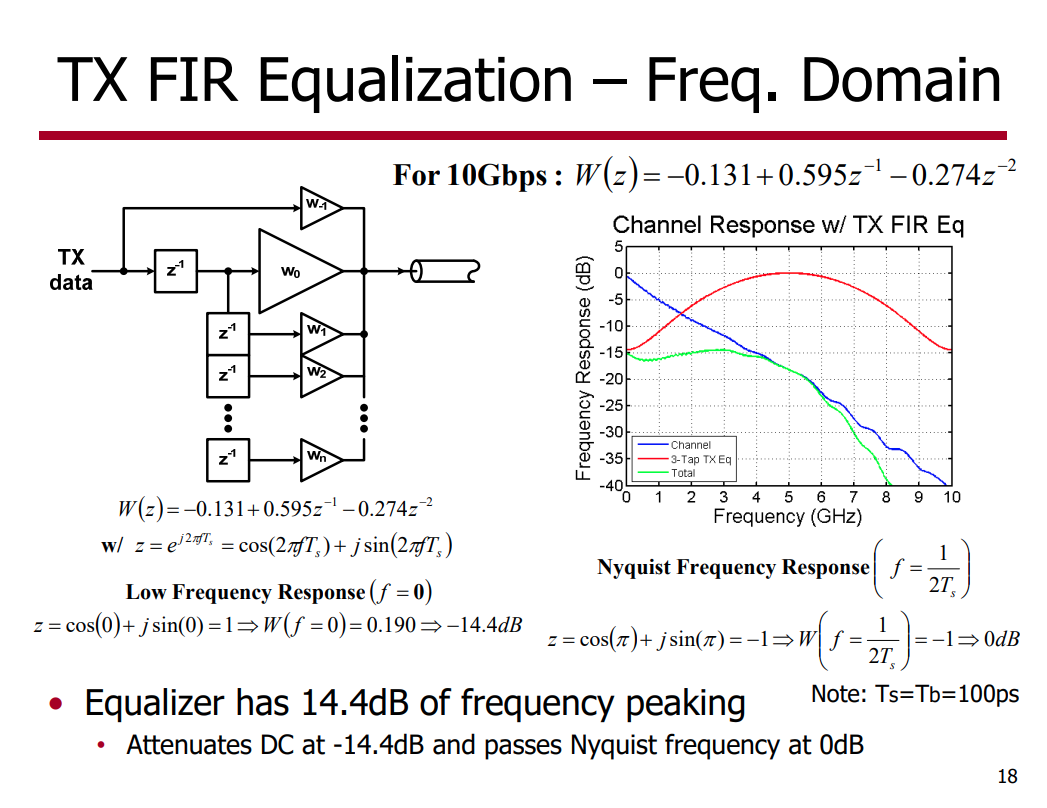image-20220322093428287 \[ z = e^{j\omega T_s} \]

Unit impulse

filter coefficients are [-0.131, 0.595, -0.274] and sampling period is 100ps

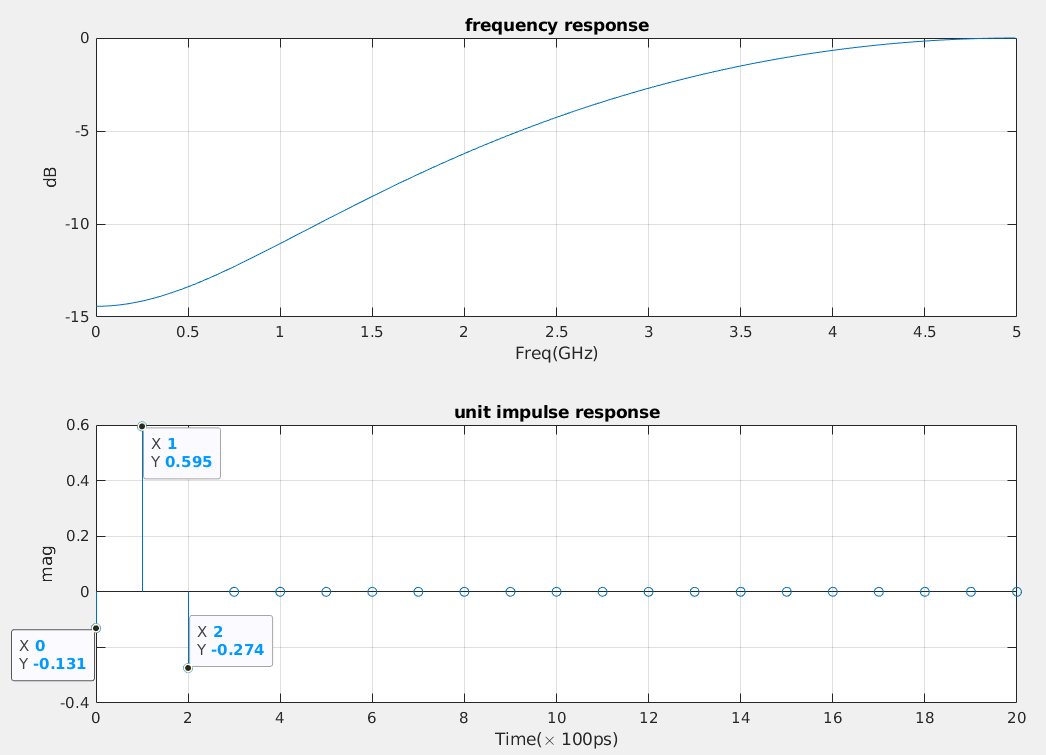
image-20220428125454912

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
%% Frequency response
w = [-0.131, 0.595, -0.274];
Ts = 100e-12;
[mag, w] = freqz(w, 1, [], 1/Ts);
subplot(2, 1, 1)
plot(w/1e9, 20*log10(abs(mag)));
xlabel('Freq(GHz)');
ylabel('dB');
grid on;
title('frequency response');

%% unit impulse response from transfer function
subplot(2, 1, 2)
z = tf('z', Ts);
h = -0.131 + 0.595*z^(-1) -0.274*z^(-2);
[y, t] = impulse(h);
stem(t*1e10, y*Ts);  % !!! y*Ts is essential
grid on;
title("unit impulse response");
xlabel('Time(\times 100ps)');
ylabel('mag');

impulse:

For discrete-time systems, the impulse response is the response to a unit area pulse of length Ts and height 1/Ts, where Ts is the sample time of the system. (This pulse approaches \(\delta(t)\) as Ts approaches zero.)

Scale output:

Multiply impulse output with sample period Ts in order to correct 1/Ts height of impulse function.

PSD transformation

If we have power spectrum or power spectrum density of both edge's absolute jitter (\(x(n)\)) , \(P_{\text{xx}}\)

Then 1UI jitter is \(x_{\text{1UI}}(n)=x(n)-x(n-1)\), and Period jitter is \(x_{\text{Period}}(n)=x(n)-x(n-2)\), which can be modeled as FIR filter, \(H(\omega) = 1-z^{-k}\), i.e. \(k=1\) for 1UI jitter and \(k=2\) Period jitter \[\begin{align} P_{\text{xx}}'(\omega) &= P_{\text{xx}}(\omega) \cdot \left| 1-z^{-k} \right|^2 \\ &= P_{\text{xx}}(\omega) \cdot \left| 1-(e^{j\omega T_s})^{-k} \right|^2 \\ &= P_{\text{xx}}(\omega) \cdot \left| 1-e^{-j\omega T_s k} \right|^2 \end{align}\]

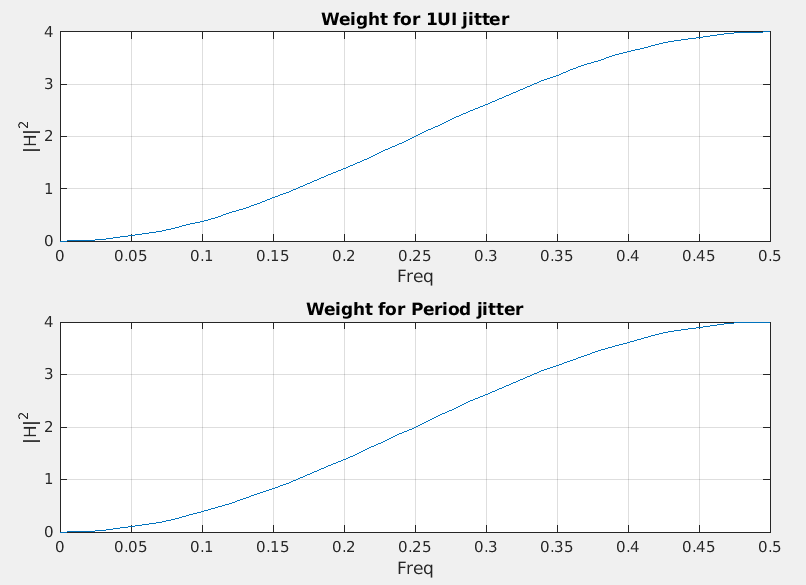
image-20220519172239916

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
clear all
close all
clc

xf_fs = 0:0.01:0.5;
k = 1;
H_1UI = 1 - exp(-1i*2*pi*xf_fs);
HH_1UI = abs(H_1UI).^2;
subplot(2, 1, 1);
plot(xf_fs, HH_1UI);
grid on;
xlabel('Freq');
ylabel('|H|^2')
title('Weight for 1UI jitter');

k = 2;
H_period = 1 - exp(-1i*2*pi*xf_fs);
HH_period = abs(H_period).^2;
subplot(2, 1, 2)
plot(xf_fs, HH_period);
grid on;
xlabel('Freq');
ylabel('|H|^2')
title('Weight for Period jitter');

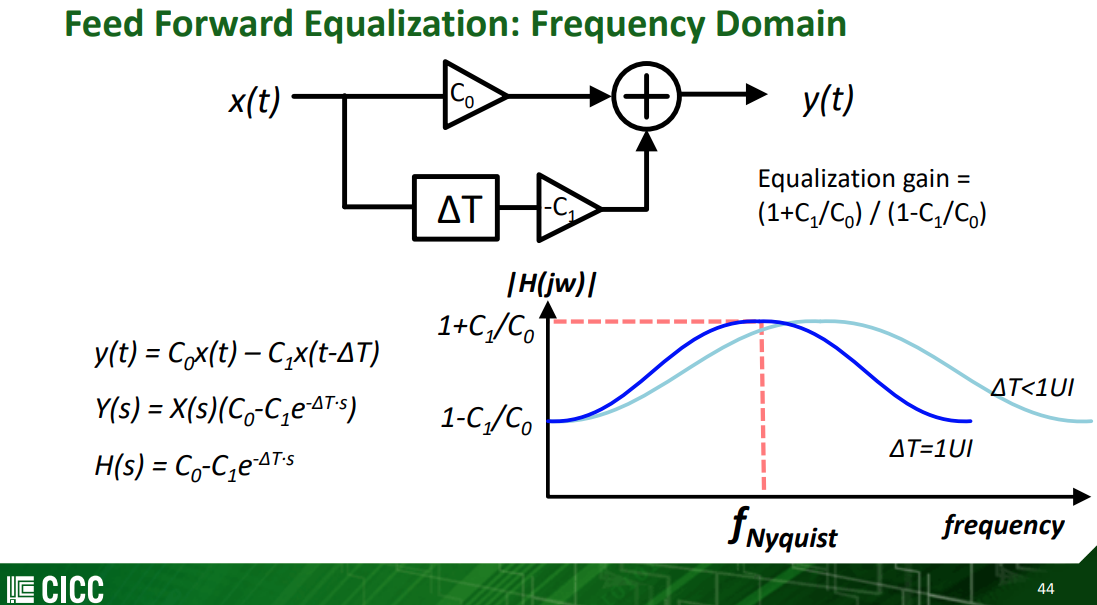image-20220709104127384 \[ x(t-\Delta T)\overset{FT}{\longrightarrow} X(s)e^{-\Delta T \cdot s} \]

reference

Sam Palermo, ECEN720, Lecture 7: Equalization Introduction & TX FIR Eq

Sam Palermo, ECEN720, Lab5 –Equalization Circuits

B. Razavi, "The z-Transform for Analog Designers [The Analog Mind]," IEEE Solid-State Circuits Magazine, Volume. 12, Issue. 3, pp. 8-14, Summer 2020.

Jhwan Kim, CICC 2022, ES4-4: Transmitter Design for High-speed Serial Data Communications

Mathuranathan. Digital filter design – Introduction https://www.gaussianwaves.com/2020/02/introduction-to-digital-filter-design/