Power Spectra and Power Spectral Densities

Posted on Edited on In

One will see the following phenomena:

  1. A power spectrum is equal to the square of the absolute value of DFT.
  2. The sum of all power spectral lines in a power spectrum is equal to the power of the input signal.
  3. The integral of a PSD is equal to the power of the input signal.

power spectrum has units of \(V^2\) and power spectral density has units of \(V^2/Hz\)

Parseval's theorem is a property of the Discrete Fourier Transform (DFT) that states: \[ \sum_{n=0}^{N-1}|x(n)|^2 = \frac{1}{N}\sum_{k=0}^{N-1}|X(k)|^2 \] Multiply both sides of the above by \(1/N\): \[ \frac{1}{N}\sum_{n=0}^{N-1}|x(n)|^2 = \frac{1}{N^2}\sum_{k=0}^{N-1}|X(k)|^2 \] \(|x(n)|^2\) is instantaneous power of a sample of the time signal. So the left side of the equation is just the average power of the signal over the N samples. \[ P_{\text{av}} = \frac{1}{N^2}\sum_{k=0}^{N-1}|X(k)|^2\text{, }V^2 \] For the each DFT bin, we can say: \[ P_{\text{bin}}(k) = \frac{1}{N^2}|X(k)|^2\text{, k=0:N-1, }V^2/\text{bin} \] This is the power spectrum of the signal.

Note that \(X(k)\) is the two-sided spectrum. If \(x(n)\) is real, then \(X(k)\) is symmetric about \(fs/2\), with each side containing half of the power. In that case, we can choose to keep just the one-sided spectrum, and multiply Pbin by 2 (except DC & Nyquist):

\[ P_{\text{bin,one-sided}}(k) = \left\{ \begin{array}{cl} \frac{1}{N^2}|X(0)|^2 & : \ k = 0 \\ \frac{2}{N^2}|X(k)|^2 & : \ 1 \leq k \leq N/2-1 \\ \frac{1}{N^2}|X(N/2)|^2 & : \ k = N/2 \end{array} \right. \]

1
2
3
4
5
6
7
8
rng default
Fs = 1000;
t = 0:1/Fs:1-1/Fs;
x = cos(2*pi*100*t) + randn(size(t));
N = length(x);
xdft = fft(x);
xsq_sum_avg = sum(x.^2)/N;
specsq_sum_avg = sum(abs(xdft).^2)/N^2;

where xsq_sum_avg is same with specsq_sum_avg

For a discrete-time sequence x(n), the DFT is defined as: \[ X(k) = \sum_{n=0}^{N-1}x(n)e^{-j2\pi kn/N} \] By it definition, the DFT does NOT apply to infinite duration signals.

scaling DFT results

spectra type unit
amplitude spectrum V
power spectrum V^2
power spectrum density V^2/Hz

Tutorial on Scaling of the Discrete Fourier Transform and the Implied Physical Units of the Spectra of Time-Discrete Signals Jens Ahrens, Carl Andersson, Patrik Höstmad, Wolfgang Kropp

Different scaling is needed to apply for amplitude spectrum, power spectrum and power spectrum density, which shown as below

image-20220427220639646

\(f_s\) in Eq.(13) is sample rate rather than frequency resolution.

And Eq.(13) can be expressed as \[ \text{PSD}(k) =\frac{1}{f_{\text{res}}\cdot N\sum_{n}w^2(n)}\left|X_{\omega}(k)\right|^2 \] where \(f_{\text{res}}\) is frequency resolution

We define the following two sums for normalization purposes:

\[\begin{align} S_1 &= \sum_{j=0}^{N-1}w_j \\ S_2 &= \sum_{j=0}^{N-1}w_j^2 \end{align}\]

Given Eq.(12) and Eq.(13) \[\begin{align} \text{PS(k)} &= \text{PSD(k)} \cdot \frac{f_s \sum_{n}w^2(n)}{(\sum_{n}\omega(n))^2} \\ &= \text{PSD(k)} \cdot f_{\text{res}} \cdot \frac{N \sum_{n}w^2(n)}{(\sum_{n}w(n))^2} \\ &= \text{PSD(k)} \cdot f_{\text{res}} \cdot \frac{N S_2}{S_1^2} \\ &= \text{PSD(k)} \cdot f_{\text{res}} \cdot \text{NENBW} \\ &= \text{PSD(k)} \cdot \text{ENBW} \end{align}\]

where Normalized Equivalent Noise BandWidth is defined as \[ \text{NENBW} =\frac{N S_2}{S_1^2} \] and Effective Noise BandWidth is \[ \text{ENBW} =f_{\text{res}} \cdot \frac{N S_2}{S_1^2} \]

For Rectangular window, \(\text{ENBW} =f_{\text{res}}\)

This equivalent noise bandwidth is required when the resulting spectrum is to be expressed as spectral density (such as for noise measurements).

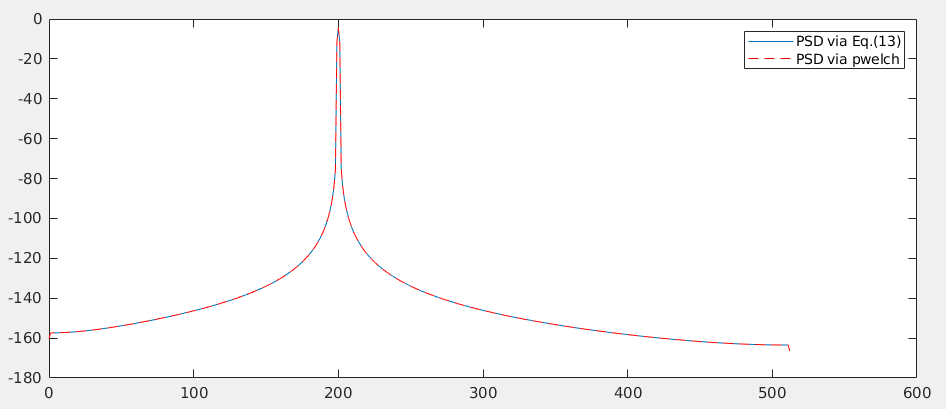
Eq.(13) Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Fs = 1024; 
t  = (0:1/Fs:1-1/Fs).'; 
x  = sin(2*pi*t*200);
Nx = length(x);
% Window data
w = hamming(Nx);	% hamming window
xw = x.*w; 
% Calculate power
nfft = Nx; 
X = fft(xw,nfft);

NumUniquePts = nfft/2+1;
Pxx1 = abs(X(1:NumUniquePts)).^2/sum(w.^2)/Fs;    %!!! Eq.(13)
Pxx1(2:end-1) = Pxx1(2:end-1)*2;    % twosided -> onesided
Fx1 = (0:NumUniquePts-1)*Fs/nfft; 

[Pxx2,Fx2] = pwelch(x,w,0,nfft,Fs);

plot(Fx1,10*log10(Pxx1),Fx2,10*log10(Pxx2),'r--');
legend('PSD via Eq.(13)','PSD via pwelch')

image-20220514165525958

window effects

It is possible to correct both the amplitude and energy content of the windowed signal to equal the original signal. However, both corrections cannot be applied simultaneously

Amplitude correction

Linear (amplitude) Spectrum \[ X(k) = \frac{X_{\omega}(k)}{S_1} \] power spectrum \[ \text{PS}=\frac{\left| X_{\omega}(k) \right|^2}{S_1^2} \]

usage: tone amplitude

Power correction

power spectral density (PSD) \[ \text{PSD} =\frac{\left|X_{\omega}(k)\right|^2}{f_s\cdot S_2} \]

We have \(\text{PSD} = \frac{\text{PS}}{\text{ENBW}}\), where \(\text{ENBW}=\frac{N \cdot S_2}{S_1^2}f_{\text{res}}\)

linear power spectrum \[ \text{PS}_L=\frac{|X_{\omega}(k)|^2}{N\cdot S_2} \]

usage: RMS value, total power \[ \text{PS}_L(k)=\text{PSD(k)} \cdot f_{\text{res}} \]

Window Correction Factors

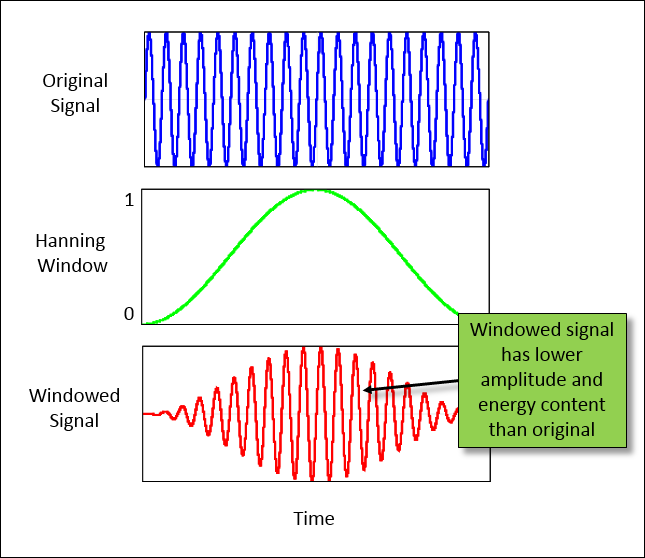
While a window helps reduce leakage (The window reduces the jumps at the ends of the repeated signal), the window itself distorts the data in two different ways:

  • Amplitude – The amplitude of the signal is reduced

    This is due to the fact that the window removes information in the signal

  • Energy – The area under the curve, or energy of the signal, is reduced

rtaImage

Window correction factors are used to try and compensate for the effects of applying a window to data. There are both amplitude and energy correction factors.

Window Type Amplitude Correction (\(K_a\)) Energy Correction (\(K_e\))
Rectangluar 1.0 1.0
hann 1.9922 1.6298
blackman 2.3903 1.8155
kaiser 1.0206 1.0204

Only the Uniform window (rectangular window), which is equivalent to no window, has the same amplitude and energy correction factors.

\[\begin{align} X(k) &= \frac{X_\omega(k)}{\sum_n w(n)} \\ &= \frac{N}{\sum_n w(n)} \frac{X_\omega(k)}{N} \\ &= K_a \cdot \frac{X_\omega(k)}{N} \end{align}\] where \(K_a = \frac{N}{\sum_n \omega(n)}\)

In literature, Coherent power gain is defined show below, which is close related to \(K_a\) \[ \text{Coherent power gain (dB)} = 20 \; log_{10} \left( \frac{\sum_n w[n]}{N} \right) \]

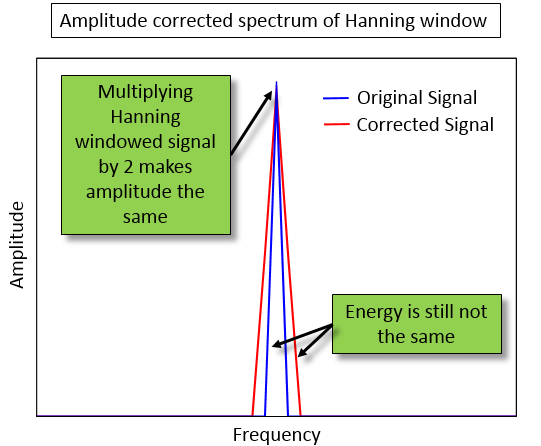
amplitude-correction

With amplitude correction, by multiplying by two, the peak value of both the original and corrected spectrum match. However the energy content is not the same.

The amplitude corrected signal (red) appears to have more energy, or area under the curve, than the original signal (blue).

\[\begin{align} \text{PSD} &=\frac{1}{f_{\text{res}}\cdot N\sum_{n}w^2(n)}\left|X_{\omega}(K)\right|^2 \\ &= \frac{N}{\sum_{n}w^2(n)} \frac{\left|X_{\omega}(K)\right|^2}{f_{\text{res}}\cdot N^2} \\ &=\left|K_e \cdot \frac{X_{\omega}(K)}{N}\right|^2 \cdot \frac{1}{f_{\text{res}}} \end{align}\]

wherer \(K_e = \sqrt{\frac{N}{\sum_{n}\omega^2(n)}}\)

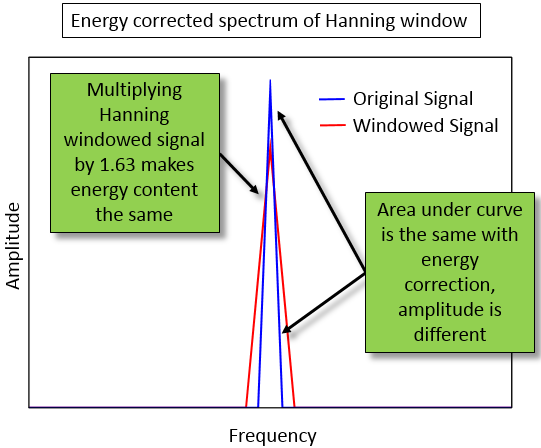
energey-correction

Multiplying the values in the spectrum by 1.63, rather than 2, makes the area under the curve the same for both the original signal (blue) and energy corrected signal (red)

hanning's correction factors:

1
2
3
4
N = 256;
w = hanning(N);
Ka = N/sum(w)
Ke = sqrt(N/sum(w.^2))
1
2
3
4
5
6
7
8
Ka =

    1.9922


Ke =

    1.6298

Amplitude,Power Correction Example

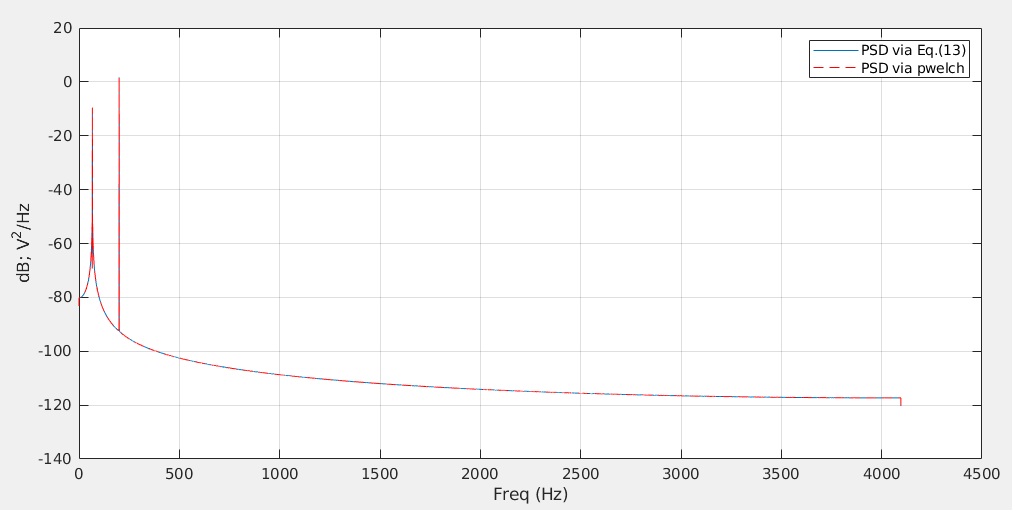
image-20220518002927545

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
%% 200 Hz, amplitude 1 and 200/3 Hz amplitude 0.3
fosc = 200;
Fs = 8192;
Nx = Fs*4;
tstop = Nx/Fs;
t  = (0:1/Fs:tstop-1/Fs).'; 
x  = sin(2*pi*t*fosc) + 0.3*sin(2*pi*t*fosc/3);
Nx = length(x);

%% direct method, time domain
P0 = sum(x.^2)/Nx;
xrms0 = sqrt(P0);   % RMS value caculated by time domain
fprintf("xrms0: %.4f\n", xrms0);

%% Window data
w = hamming(Nx);	% hamming window
%w = ones(Nx, 1);	% rectangular window

S1= sum(w);
S2 = sum(w.^2);
NENBW = Nx*S2/S1^2;

xw = x.*w; 
nfft = Nx; 
X = fft(xw,nfft);   % windowed signal fft
NumUniquePts = nfft/2+1;
Fx1 = (0:NumUniquePts-1)*Fs/nfft;

%% fft - ps -> rms
Xmag = abs(X);
PS1 = Xmag.^2/S1^2;    %!!! Eq.(12)
PS1 = PS1(1:NumUniquePts);
PS1(2:end-1) = PS1(2:end-1)*2;    % twosided -> onesided
Pmax_fft = max(PS1);    % !!! amplitude OK
fprintf("Pmax_fft: %.4f\n", Pmax_fft);

% linear power spectrum
PSL_fft = Xmag.^2/nfft/S2;
PSL_fft = PSL_fft(1:NumUniquePts);
PSL_fft = PSL_fft(2:end-1)*2;
Ptot_fft1 = sum(PSL_fft);
xrms_PSL = sqrt(Ptot_fft1); % !!! power OK
fprintf("xrms_PSL: %.4f\n", xrms_PSL);

% use psd*fres to calculate total power
Pxx1 = abs(X(1:NumUniquePts)).^2/sum(w.^2)/Fs;    %!!! Eq.(13)
Pxx1(2:end-1) = Pxx1(2:end-1)*2;    % twosided -> onesided
Ptot_fft2 = sum(Pxx1*Fs/nfft);
xrms_psd = sqrt(Ptot_fft2);     % !!! power OK
fprintf("xrms_psd: %.4f\n", xrms_psd);


%% pwelch
[Pxx2,Fx2] = pwelch(x,w,0,nfft,Fs);
fres = Fx2(2)-Fx2(1);

PS2 = Pxx2*fres;
Ptot_pwelch = sum(PS2);
xrms_pwelch = sqrt(Ptot_pwelch);    % !!! amplitude OK
fprintf("xrms_pwelch: %.4f\n", xrms_pwelch);

% PS = PSD * ENBW always hold
ENBW = fres * NENBW;
PS2_pwelch = Pxx2*ENBW;
Pmax_pwelch = max(PS2_pwelch);  % !!! amplitude OK
fprintf("Pmax_pwelch: %.4f\n", Pmax_pwelch);

%% plot psd of two methods
plot(Fx1,10*log10(Pxx1),Fx2,10*log10(Pxx2),'r--');
legend('PSD via Eq.(13)','PSD via pwelch')
grid on;
xlabel('Freq (Hz)');
ylabel('dB; V^2/Hz')
1
2
3
4
5
6
xrms0: 0.7383
Pmax_fft: 0.5000
xrms_PSL: 0.7382
xrms_psd: 0.7382
xrms_pwelch: 0.7382
Pmax_pwelch: 0.5000

RMS

We may also want to know for example the RMS value of the signal, in order to know how much power the signal generates. This can be done using Parseval’s theorem.

For a periodic signal, which has a discrete spectrum, we obtain its total RMS value by summing the included signals using \[ x_{\text{rms}}=\sqrt{\sum R_{xk}^2} \] Where \(R_{xk}\) is the RMS value of each sinusoid for \(k=1,2,3,...\) The RMS value of a signal consisting of a number of sinusoids is consequently equal to the square root of the sum of the RMS values.

This result could also be explained by noting that sinusoids of different frequencies are orthogonal, and can therefore be summed like vectors (using Pythagoras’ theorem)

For a random signal we cannot interpret the spectrum in the same way. As we have stated earlier, the PSD of a random signal contains all frequencies in a particular frequency band, which makes it impossible to add the frequencies up. Instead, as the PSD is a density function, the correct interpretation is to sum the area under the PSD in a specific frequency range, which then is the square of the RMS, i.e., the mean-square value of the signal \[ x_{\text{rms}}=\sqrt{\int G_{xx}(f)df}=\sqrt{\text{area under the curve}} \] The linear spectrum, or RMS spectrum, defined by \[\begin{align} X_L(k) &= \sqrt{\text{PSD(k)} \cdot f_{\text{res}}}\\ &=\sqrt{\frac{\left|X_{\omega}(k)\right|^2}{f_{\text{res}}\cdot N\sum_{n}\omega^2(n)} \cdot f_{\text{res}}} \\ &= \sqrt{\frac{\left|X_{\omega}(k)\right|^2}{N\sum_{n}\omega^2(n)}} \\ &= \sqrt{\frac{|X_{\omega}(k)|^2}{N\cdot S_2}} \end{align}\]

The corresponding linear power spectrum or RMS power spectrum can be defined by \[\begin{align} \text{PS}_L(k)&=X_L(k)^2=\frac{|X_{\omega}(k)|^2}{S_1^2}\frac{S_1^2}{N\cdot S_2} \\ &=\text{PS}(k) \cdot \frac{S_1^2}{N\cdot S_2} \end{align}\]

So, RMS can be calculated as below \[\begin{align} P_{\text{tot}} &= \sum \text{PS}_L(k) \\ \text{RMS} &= \sqrt{P_{\text{tot}}} \end{align}\]

DFT averaging

we use \(N= 8*\text{nfft}\) time samples of \(x\) and set the number of overlapping samples to \(\text{nfft}/2 = 512\). pwelch takes the DFT of \(\text{Navg} = 15\) overlapping segments of \(x\), each of length \(\text{nfft}\), then averages the \(|X(k)|^2\) of the DFT’s.

In general, if there are an integer number of segments that cover all samples of N, we have \[ N = (N_{\text{avg}}-1)*D + \text{nfft} \] where \(D=\text{nfft}-\text{noverlap}\). For our case, with \(D = \text{nfft}/2\) and \(N/\text{nfft} = 8\), we have \[ N_{\text{avg}}=2*N/\text{nfft}-1=15 \] For a given number of time samples N, using overlapping segments lets us increase \(N_{avg}\) compared with no overlapping. In this case, overlapping of 50% increases \(N_{avg}\) from 8 to 15. Here is the Matlab code to compute the spectrum:

1
2
3
4
5
6
7
8
nfft= 1024;
N= nfft*8;                                % number of samples in signal
n= 0:N-1;
x= A*sin(2*pi*f0*n*Ts) + .1*randn(1,N);   % 1 W sinewave + noise
noverlap= nfft/2;                         % number of overlapping time samples
window= hanning(nfft);
[pxx,f]= pwelch(x,window,noverlap,nfft,fs);  % W/Hz  PSD
PdB_bin= 10*log10(pxx*fs/nfft);              % dBW/bin

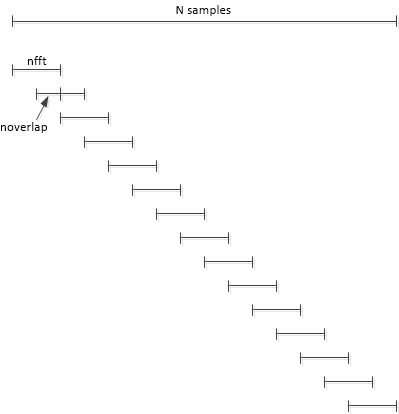
figure 3_99153

DFT averaging reduces the variance \(\sigma^2\) of the noise spectrum by a factor of \(N_{avg}\), as long as noverlap is not greater than nfft/2

image-20220420013255660

image-20230526011628682

fftshift

The result of fft and its index is shown as below

complexDFT_Matlab_index

After fftshift

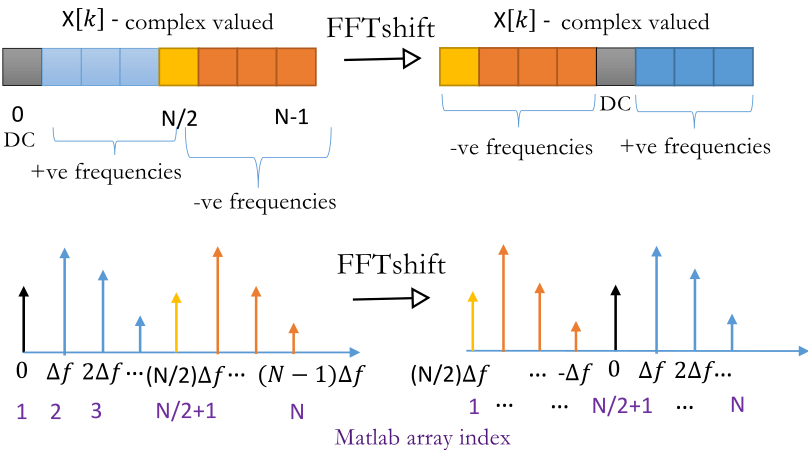
FFTshift_Matlab_index_resolved

1
2
3
4
5
>> fftshift([1 2 3 4 5 6])

ans =

     4     5     6     1     2     3

dft and psd function in virtuoso

  • dft always return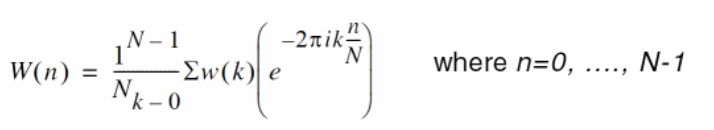

    image-20230525011604685

To compensate windowing effect, \(W(n)\), the dft output should be multiplied by \(K_a\), e.g. 1.9922 for hanning window.

  • psd function has taken into account \(K_e\), postprocessing is not needed

reference

Demonstration-DFT-PS-PSD

mathworks, Power Spectral Density Estimates Using FFT

Lyons, Richard, “Widowing Functions Improve FFT Results”, EDN, June 1, 1998. https://www.edn.com/electronics-news/4383713/Windowing-Functions-Improve-FFT-Results-Part-I

Rapuano, Sergio, and Harris, Fred J., An Introduction to FFT and Time Domain Windows, IEEE Instrumentation and Measurement Magazine, December, 2007. https://ieeexplore.ieee.org/document/4428580

Neil Robertson, The Power Spectrum

Neil Robertson, Use Matlab Function pwelch to Find Power Spectral Density – or Do It Yourself

Neil Robertson, Evaluate Window Functions for the Discrete Fourier Transform

Mathuranathan Viswanathan, Interpret FFT, complex DFT, frequency bins & FFTShift

robert bristow-johnson, Does windowing affect Parseval's theorem?

Heinzel, Gerhard, A. O. Rüdiger and Roland Schilling. "Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new at-top windows." (2002). URL: https://holometer.fnal.gov/GH_FFT.pdf

Window Correction Factors URL: https://community.sw.siemens.com/s/article/window-correction-factors

Brandt, A, 2011. Noise and vibration analysis: signal analysis and experimental procedures. John Wiley & Sons

What should be the correct scaling for PSD calculation using fft. URL:https://dsp.stackexchange.com/a/32205

POWER SPECTRAL DENSITY CALCULATION VIA MATLAB Revision C. URL: http://www.vibrationdata.com/tutorials_alt/psd_mat.pdf

Jens Ahrens, Carl Andersson, Patrik Höstmad, Wolfgang Kropp, “Tutorial on Scaling of the Discrete Fourier Transform and the Implied Physical Units of the Spectra of Time-Discrete Signals” in 148th Convention of the AES, e-Brief 56, May 2020 [ pdf, web ].

Manolakis, D., & Ingle, V. (2011). Applied Digital Signal Processing: Theory and Practice. Cambridge: Cambridge University Press. doi:10.1017/CBO9780511835261