Jitters Simulation for Driven Circuit

Posted on Edited on In

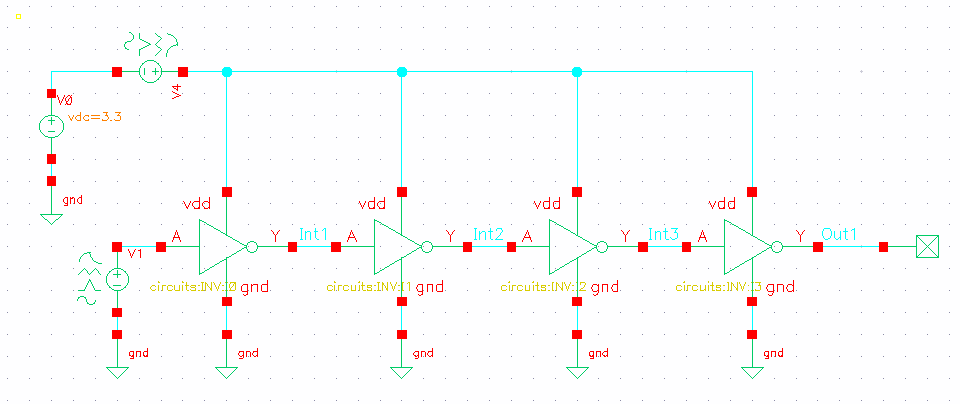
image-20220516004008878

Deterministic Jitter

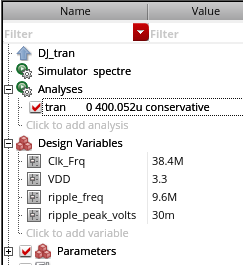
image-20220516004058916

image-20220516004206118

j_Djpp can be calculated by PSD,too

image-20220516004615033

1
2
3
4
5
6
7
8
9
fck = 38.4e6;
Nfft = 15000;
fres = fck/Nfft;
psddBc = -99.3343;
psBc = psddBc + 10*log10(fres);	% psd -> ps; 
phrad2 = 10^(psBc/10);
phrms = sqrt(phrad2);
Jrms = phrms/2/pi*1/fck;
Jpp = 2*sqrt(2)*Jrms;
1
2
3
Jpp =

   6.4038e-12

For DJ, we usually use peak to peak value

BTW, the psd value at half of fundamental frequency (\(f_s/2\)) is duty cycle distortion due to the NMOS/PMOS imbalance, because of rising only data

Random Jitter

RJ can be accurately and efficiently measured using PSS/Pnoise or HB/HBnoise.

Note that the transient noise can also be used to compute RJ;

However, the computation cost is typically very high, and the accuracy is lesser as compared to PSS/Pnoise and HB/HBnoise.

Since RJ follows a Gaussian distribution, it can be fully characterized using its Root-Mean-Squared value (RMS) or the standard deviation value (\(\sigma\))

The Peak-to-Peak value of RJ (\(\text{RJ}_{\text{p-p}}\)) can be calculated under certain observation conditions \[ \text{RJ}_{\text{p-p}}\equiv K \ast \text{RJ}_{\text{RMS}} \] Here, \(K\) is a constant determined by the BER specification of the system given in the following Table

BER Crest factor (K)
\(10^{-3}\) 6.18
\(10^{-4}\) 7.438
\(10^{-5}\) 8.53
\(10^{-6}\) 9.507
\(10^{-7}\) 10.399
\(10^{-8}\) 11.224
\(10^{-9}\) 11.996
\(10^{-10}\) 12.723
\(10^{-11}\) 13.412
\(10^{-12}\) 14.069
\(10^{-13}\) 14.698 
1
2
3
4
K = 14.698;
Ks = K/2;
p = normcdf([-Ks Ks]);
BER = 1 - (p(2)-p(1));
1
2
3
BER =

   1.9962e-13

image-20220516160050961

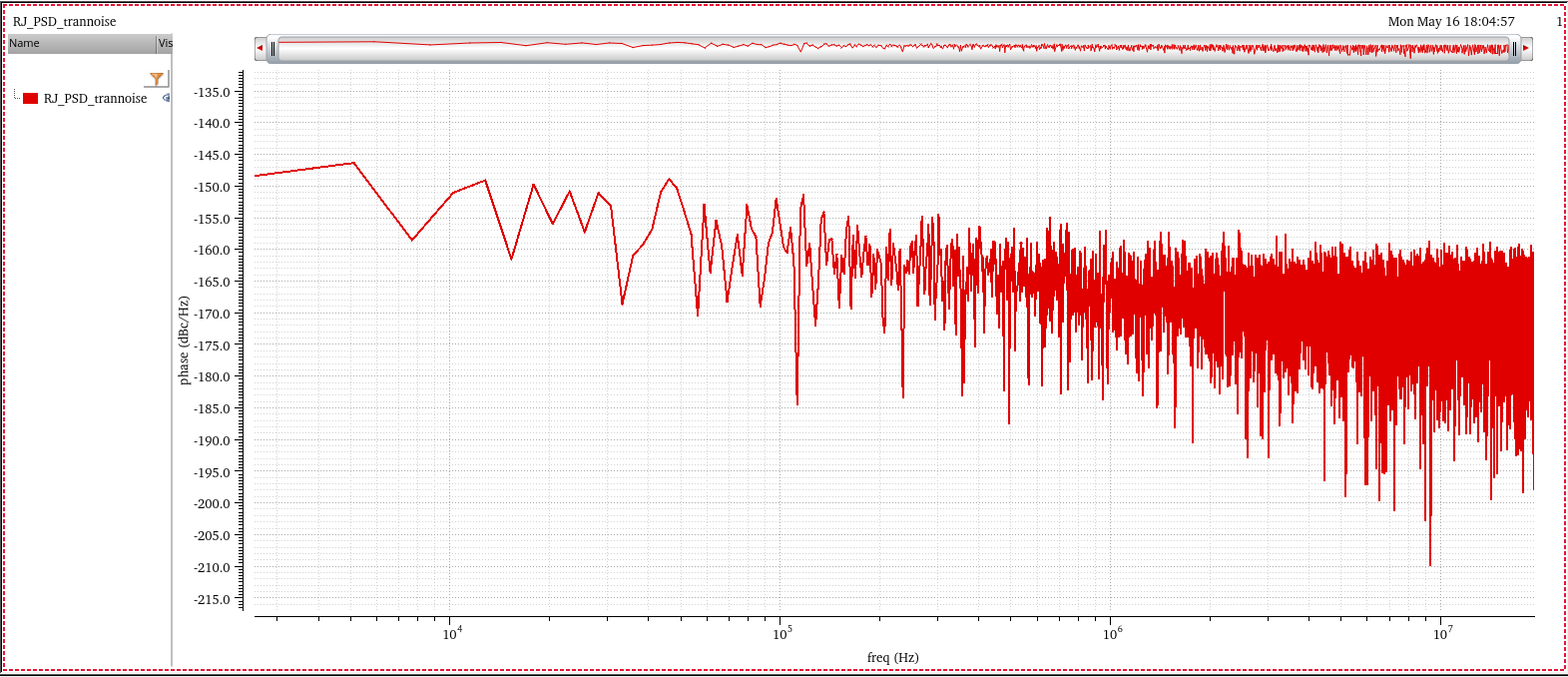
image-20220516193125490

Total Jitter

\[ \text{TJ}_{\text{p-p}}\equiv \text{DJ}_{\text{p-p}} + \text{RJ}_{\text{p-p}}(\text{BER}) \]

tj.drawio

image-20220516160006909

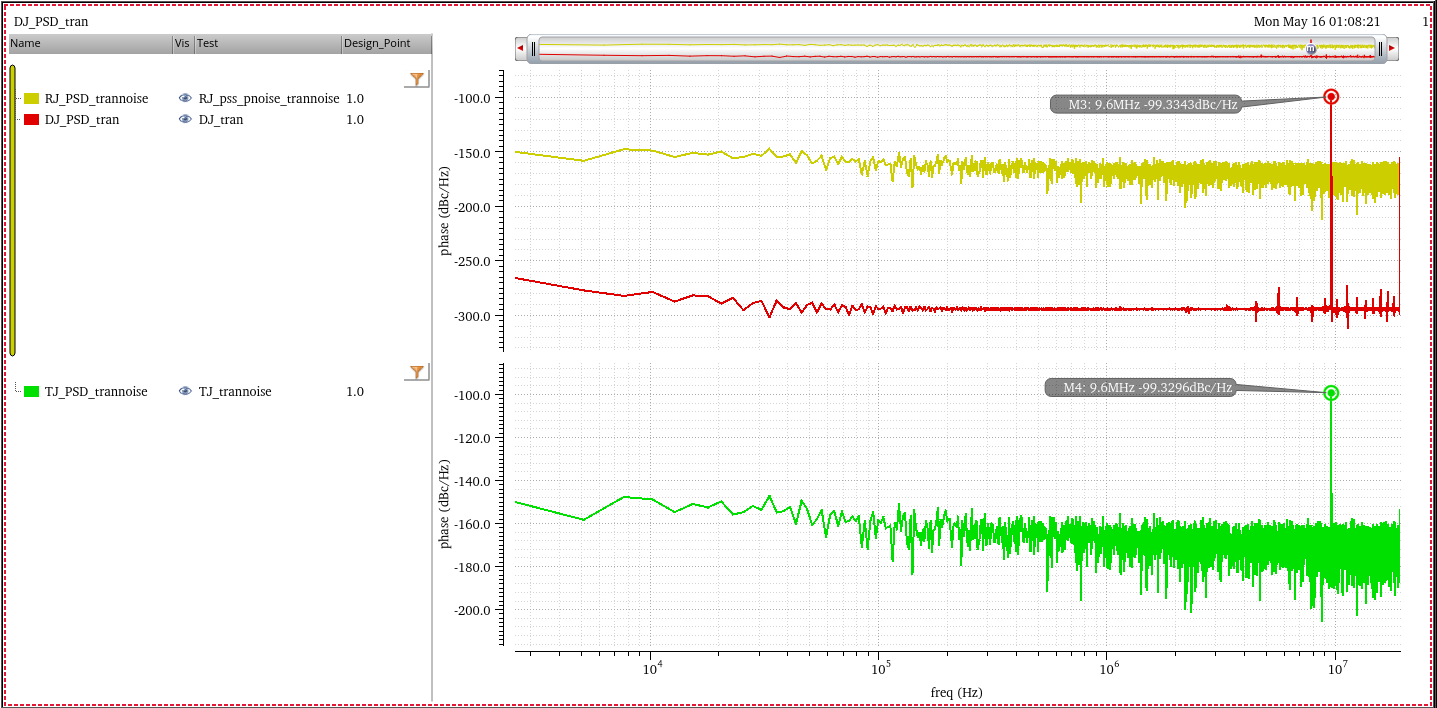
image-20220516012200383

In the psd of TJ, the spur is DJ and floor is RJ

Phase Noise to Jitter

The phase noise is traditionally defined as the ratio of the power of the signal in 1Hz bandwidth at offset \(f\) from the carrier \(P\), divided by the power of the carrier \[ \ell (f) = \frac {S_v'(f_0+f)}{P} \] where \(S_v'\) is is one-sided voltage PSD and \(f \geqslant 0\)

Under narrow angle assumption \[ S_{\varphi}(f)= \frac {S_v'(f_0+f)}{P} \] where \(\forall f\in \left[-\infty +\infty\right]\)

Using the Wiener-Khinchin theorem, it is possible to easily derive the variance of the absolute jitter(\(J_{ee}\))via integration of the corresponding PSD \[ J_{ee,rms}^2 = \int S_{J_{ee}}(f)df \]

And we know the relationship between absolute jitter and excess phase is \[ J_{ee}=\frac {\varphi}{\omega_0} \] Considering that phase noise is normally symmetrical about the zero frequency, multiplied by two is shown as below \[ J_{ee,rms} = \frac{\sqrt{2\int_{0}^{+\infty}\ell(f)df}}{\omega_0} \] where phase noise is in linear units not in logarithmic ones.

Because the unit of phase noise in Spectre-RF is logarithmic unit (dBc), we have to convert the unit before applying the above equation \[ \ell[linear] = 10^{\frac {\ell [dBc/Hz]}{10}} \] The complete equation using the simulation result of Spectre-RF Pnoise is \[ J_{ee,rms} = \frac{\sqrt{2\int_{0}^{+\infty}10^{\frac {\ell [dBc/Hz]}{10}}df}}{\omega_0} \]

The above equation has been verified for sampled pnoise, i.e. Jee and Edge Phase Noise.

  • For pnoise-sampled(jitter), Direct Plot Form - Function: Jee:Integration Limits can calculate it conveniently
  • But for pnoise-timeaveage, you have to use the below equation to get RMS jitter.

One example, integrate to \(\frac{f_{osc}}{2}\) and \(f_{osc} = 16GHz\)

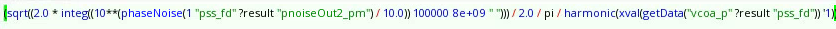
image-20220415100034220

Of course, it apply to conventional pnoise simulation.

On the other hand, output rms voltage noise, \(V_{out,rms}\) divied by slope should be close to \(J_{ee,rms}\) \[ J_{ee,rms} = \frac {V_{out,rms}}{slope} \]

Pulse Width Jitter (PWJ)

[Spectre Tech Tips: Measuring Noise in Digital Circuits]

Pnoise sampled: Edge Delay mode measures the noise defined by two edges. Both edges are defined by a threshold voltage and rising or falling edges, which measures the noise of the pulse itself and direct plot calculate the variation of the pulse width

reference

Article (20500632) Title: How to simulate Random and Deterministic Jitters URL: https://support.cadence.com/apex/ArticleAttachmentPortal?id=a1O3w000009fiXeEAI

Spectre Tech Tips: Measuring Noise in Digital Circuits - Analog/Custom Design - Cadence Blogs - Cadence Community https://community.cadence.com/cadence_blogs_8/b/cic/posts/s . . .

J. Kim et al., "A 112 Gb/s PAM-4 56 Gb/s NRZ Reconfigurable Transmitter With Three-Tap FFE in 10-nm FinFET," in IEEE Journal of Solid-State Circuits, vol. 54, no. 1, pp. 29-42, Jan. 2019, doi: 10.1109/JSSC.2018.2874040

— et al., "A 224-Gb/s DAC-Based PAM-4 Quarter-Rate Transmitter With 8-Tap FFE in 10-nm FinFET," in IEEE Journal of Solid-State Circuits, vol. 57, no. 1, pp. 6-20, Jan. 2022, doi: 10.1109/JSSC.2021.3108969