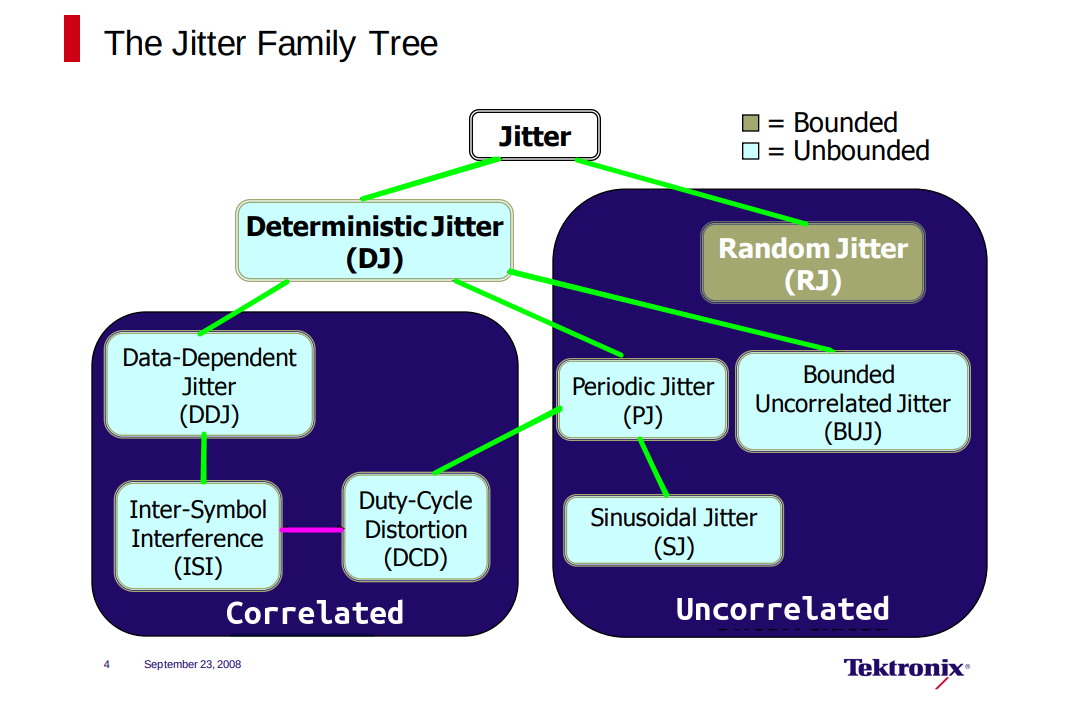
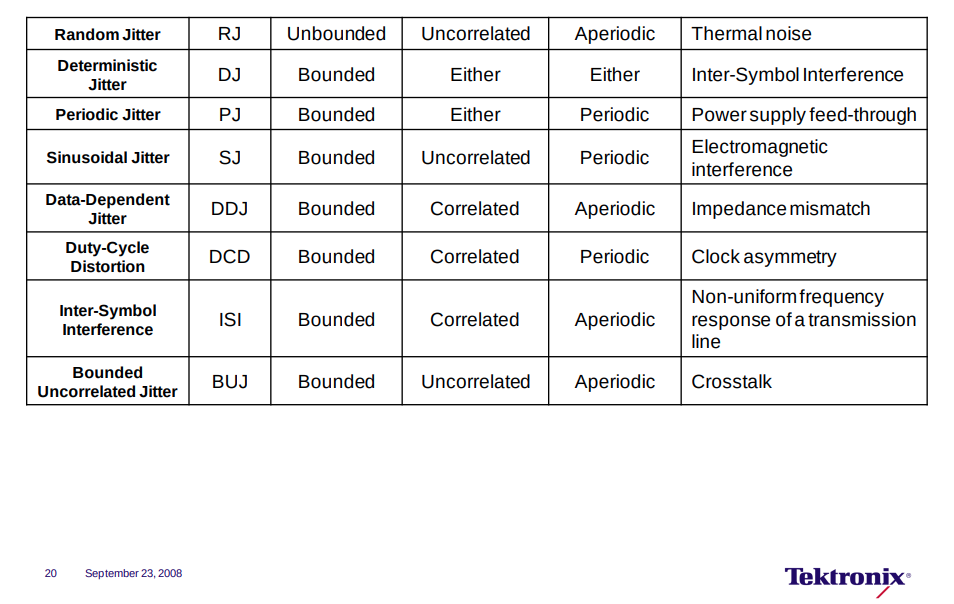
Jitter
Phase Noise to Jitter
Note that \(L(f )\) is defined over positive frequencies only \((f \ge 0)\)
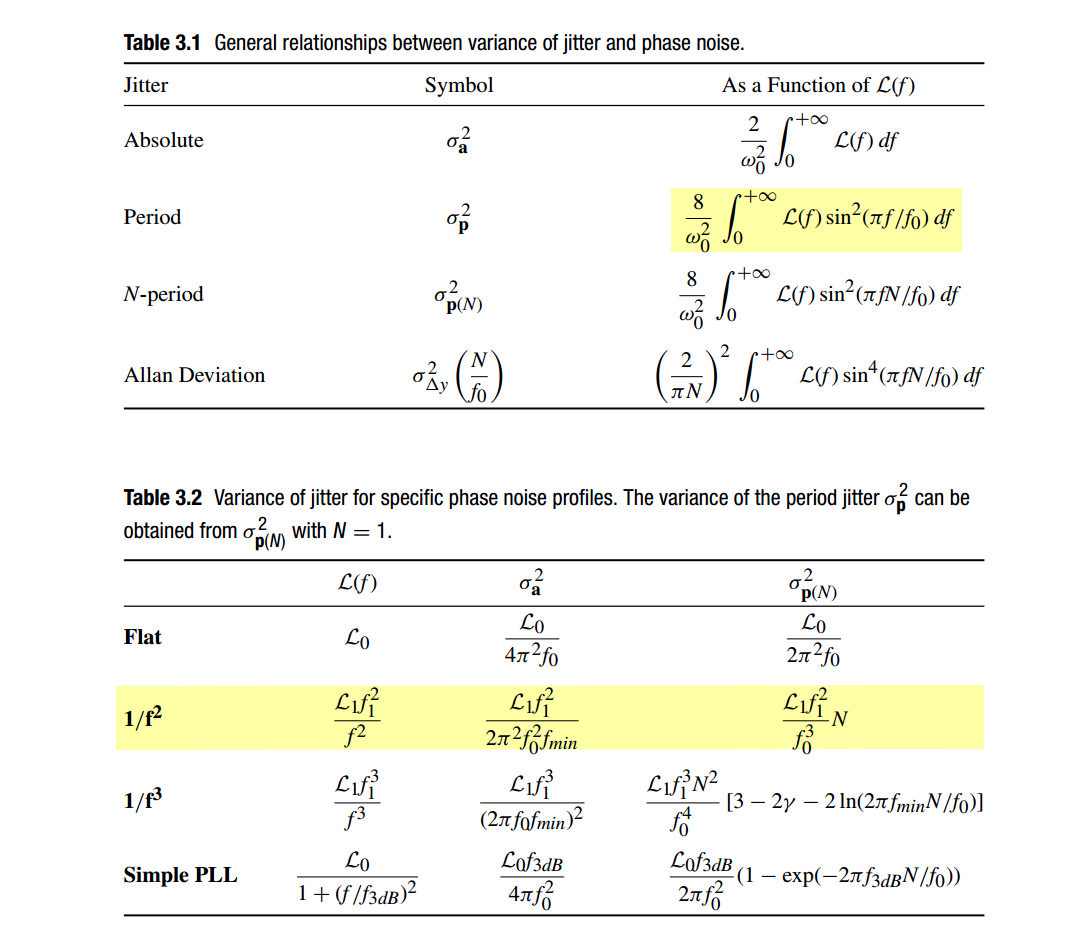
for simple PLL
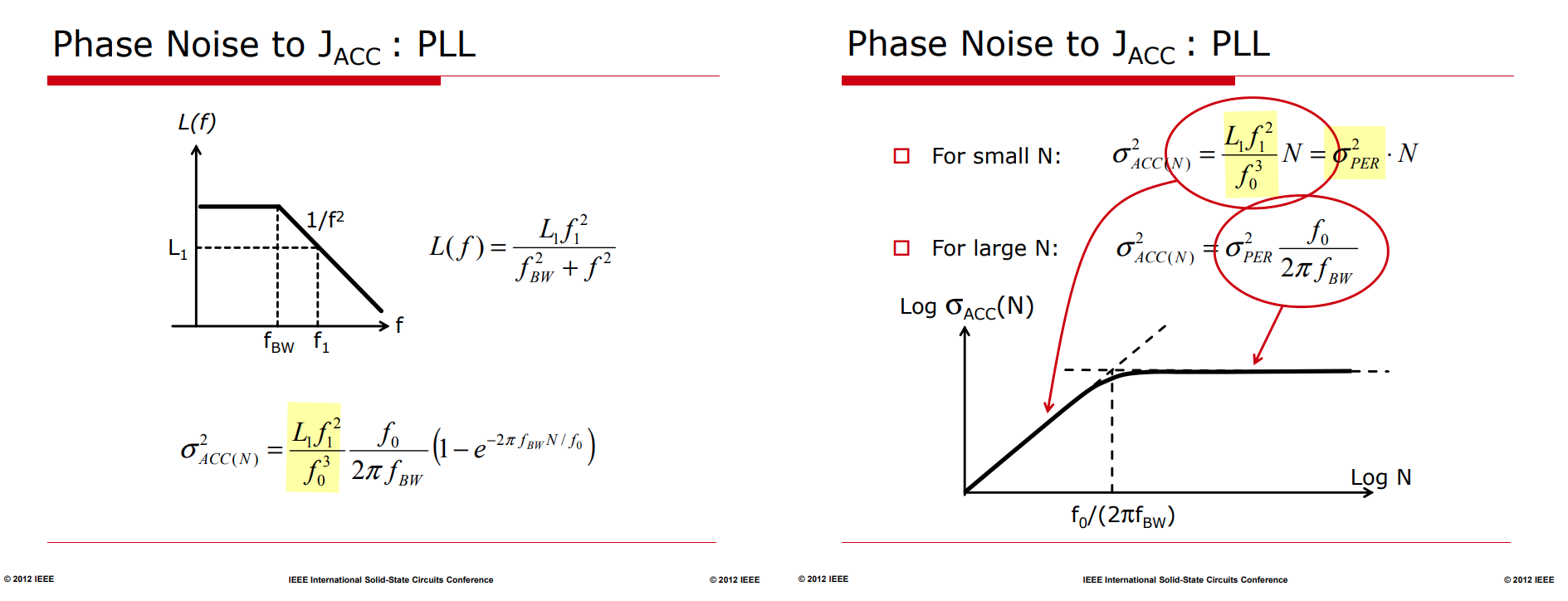
For small \(N\): \(\sigma_{p(N)}^2 \approx \frac{\mathcal{L}_0 f_{3dB}}{2\pi f_0^2} \cdot \frac{2\pi f_{3dB}N}{f_0}=\frac{\mathcal{L}_0f_{3dB}^2}{f_0^3}=\sigma_{PER}^2\)
For large \(N\): \(\sigma_{p(N)}^2 \approx \frac{\mathcal{L}_0f_{3dB}^2}{f_0^3} \cdot \frac{f_0}{2\pi f_{3dB}}=\sigma_{PER}^2\cdot \frac{f_0}{2\pi f_{3dB}}\)
Free Running OSC OSC in simple PLL \(\mathcal{L}(f) = \frac{\mathcal{L}_0 f_{3dB}^2}{f^2}\) \(\mathcal{L}(f) = \frac{\mathcal{L}_0 f_{3dB}^2}{f^2 + f_{3dB}^2}\)
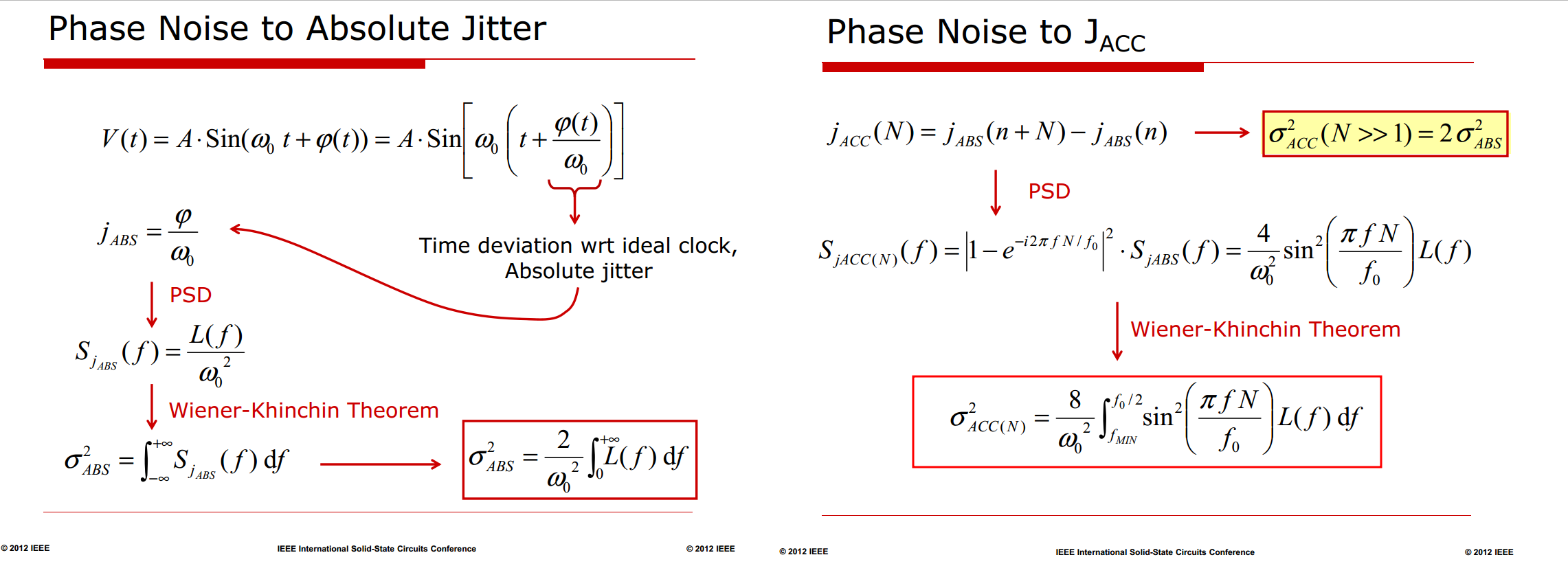 \[\begin{align}
S_{jACC(N)}(f) &= |1-z^{-N}|^2\cdot S_{jABS}(f) \\
&= |1-\cos\theta +j\sin\theta|^2\cdot S_{jABS}(f) =
((1-\cos\theta)^2 + \sin^2\theta)\cdot S_{jABS}(f) \\
&= 2(1-\cos\theta)\cdot S_{jABS}(f) = 4\sin^2(\theta/2)\cdot
S_{jABS}(f)
\end{align}\]
\[\begin{align}
S_{jACC(N)}(f) &= |1-z^{-N}|^2\cdot S_{jABS}(f) \\
&= |1-\cos\theta +j\sin\theta|^2\cdot S_{jABS}(f) =
((1-\cos\theta)^2 + \sin^2\theta)\cdot S_{jABS}(f) \\
&= 2(1-\cos\theta)\cdot S_{jABS}(f) = 4\sin^2(\theta/2)\cdot
S_{jABS}(f)
\end{align}\]
where \(\theta = 2\pi f N/f_0\)

As EQ(3.44), EQ(3.45)
the autocorrelation is the inverse Fouer transform of the PSD
\[ R_{\varphi}(t) = \int_{-\infty}^{+\infty} S_{\varphi} (f) e^{j2\pi f t} df \]
Then, \[\begin{align} R_{\varphi}(0) &= \int_{-\infty}^{+\infty} S_{\varphi} (f) df \\ R_{\varphi}(NT_0) &= \int_{-\infty}^{+\infty} S_{\varphi} (f) e^{j2\pi f NT_0} df \end{align}\]
Thus, yield EQ(3.48)

Simplified PLL Phase Noise Profile
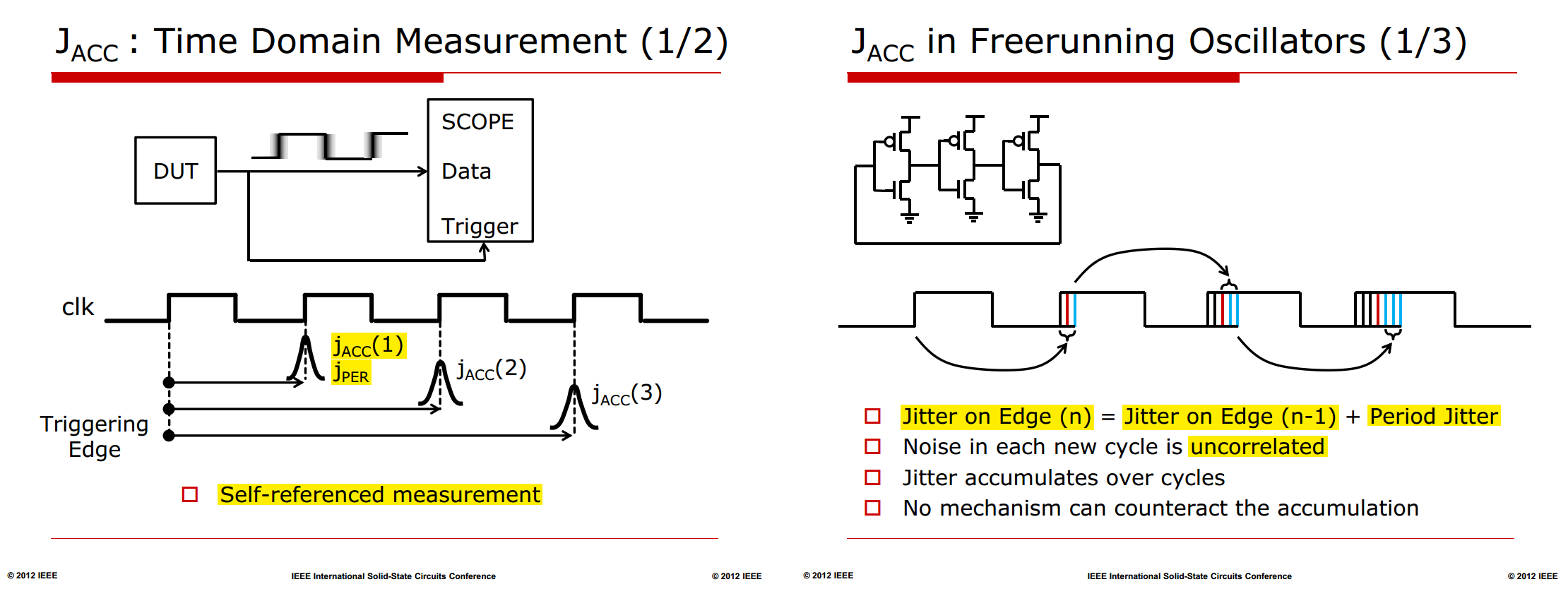
Absolute Jitter
TODO 📅
Period Jitter
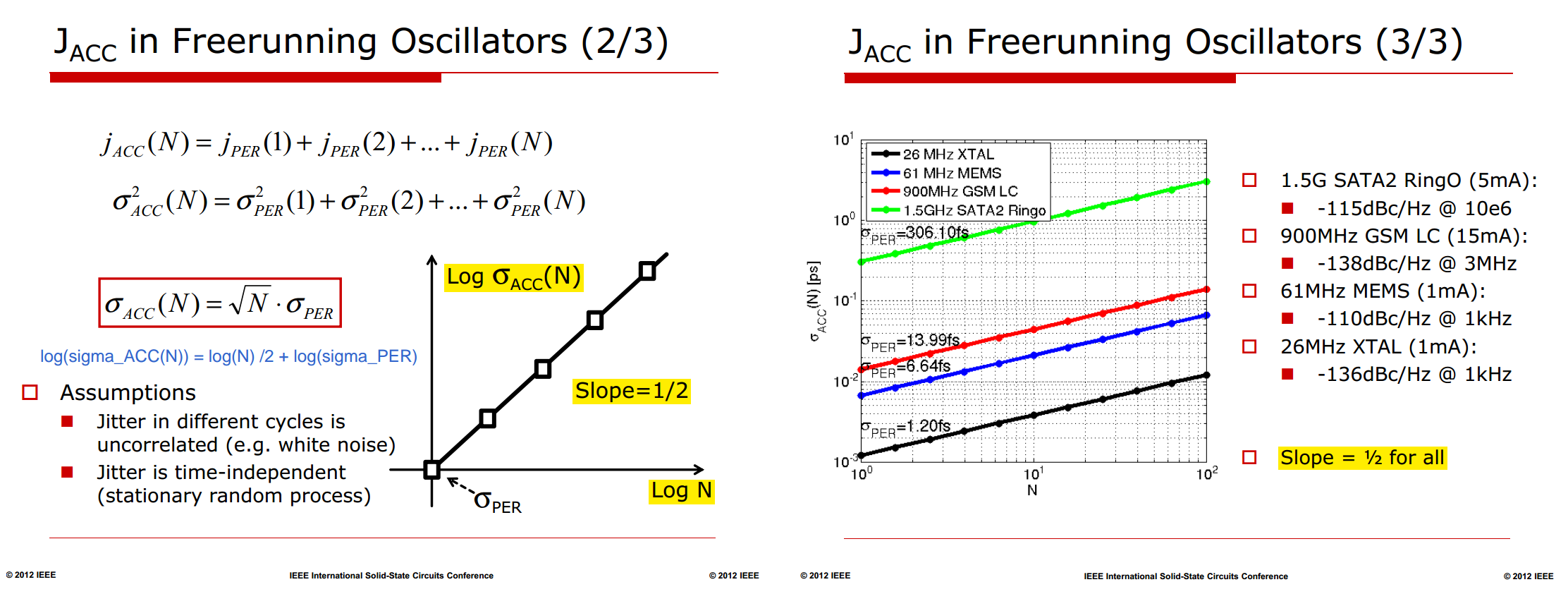
a random-walk DCO - \(1/f^2\) Phase Noise Profile
L. Avallone, M. Mercandelli, A. Santiccioli, M. P. Kennedy, S. Levantino and C. Samori, "A Comprehensive Phase Noise Analysis of Bang-Bang Digital PLLs," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 68, no. 7, pp. 2775-2786, July 2021 [https://sci-hub.st/10.1109/TCSI.2021.3072344]

Mozhgan Mansuri “Low-Power Low-Jitter On-Chip Clock Generation” thesis UCLA [https://people.engr.tamu.edu/spalermo/ecen689/pll_thesis_mansuri_ucla_2003.pdf]
[https://people.engr.tamu.edu/spalermo/ecen689/PRBS_&_PLL_model.pdf]

Even-odd Jitter (EOJ)
| Jitter measurement | Description |
|---|---|
| F/2 | F/2 is the peak-to-peak amplitude of the periodic jitter occurring at 1/2 of the data rate. |
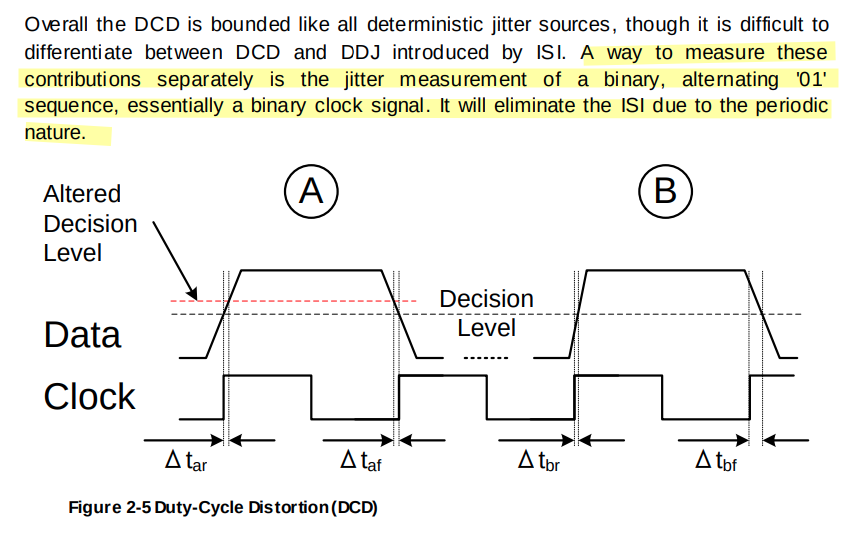
Even-odd jitter, also known as F/2 jitter, arises from a clock signal's duty cycle not being perfectly 50%

Even-odd jitter has been referred to as duty cycle distortion by other Physical Layer specifications for operation over electrical backplane or twinaxial copper cable assemblies
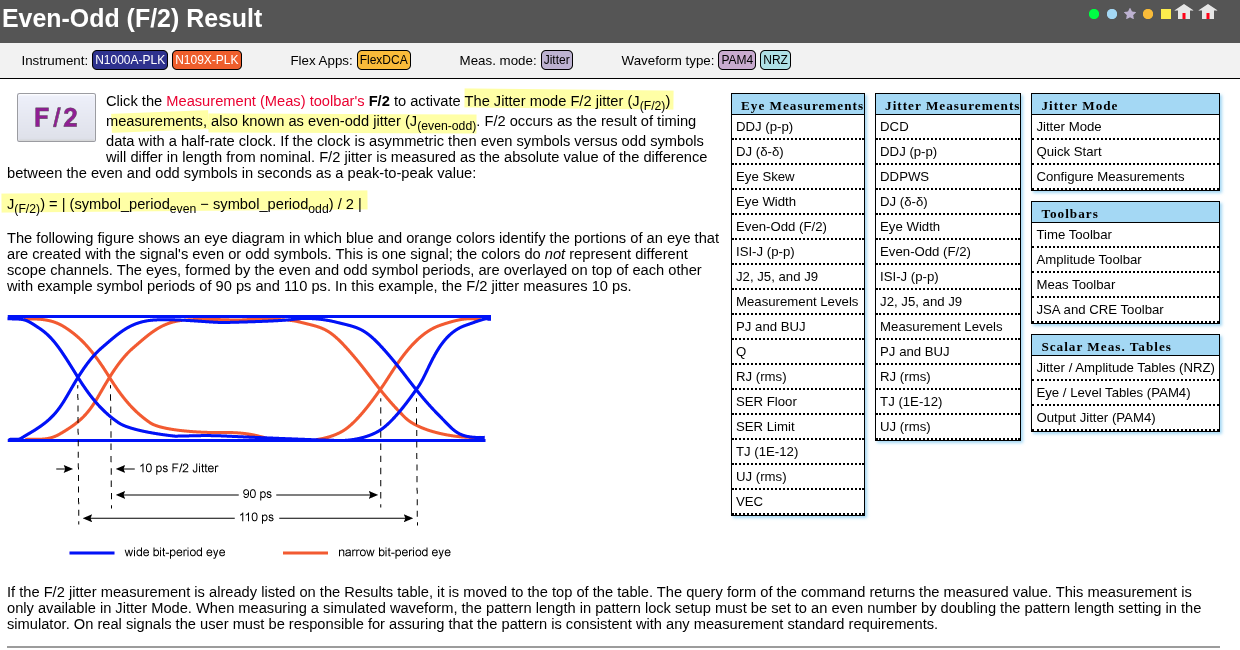

Comparing DCD and F/2 Jitter Using a BERTScope® Bit Error Rate Testing Application Note [https://download.tek.com/document/65W_26040_0_Letter.pdf]
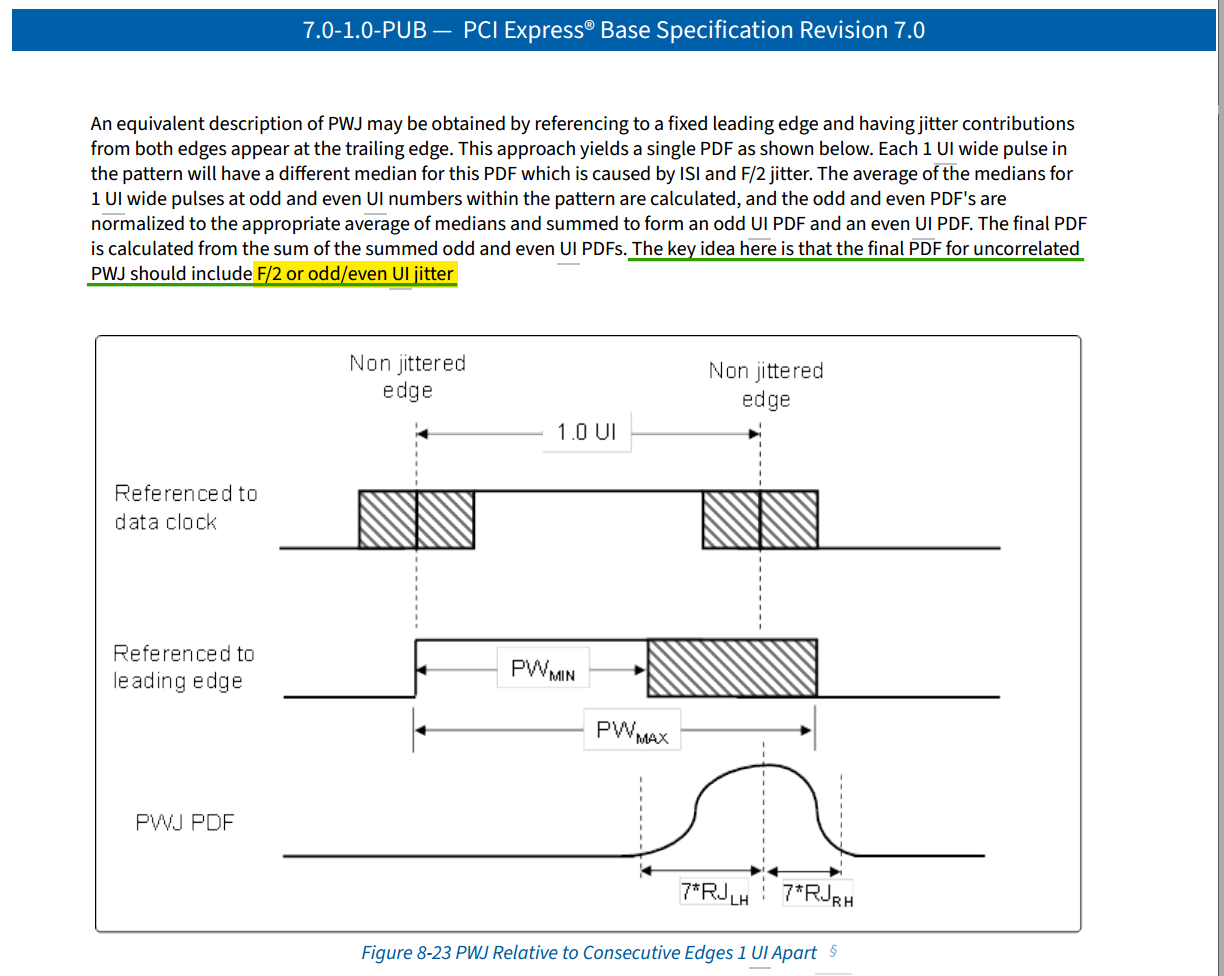
Pulse Width Jitter (PWJ)
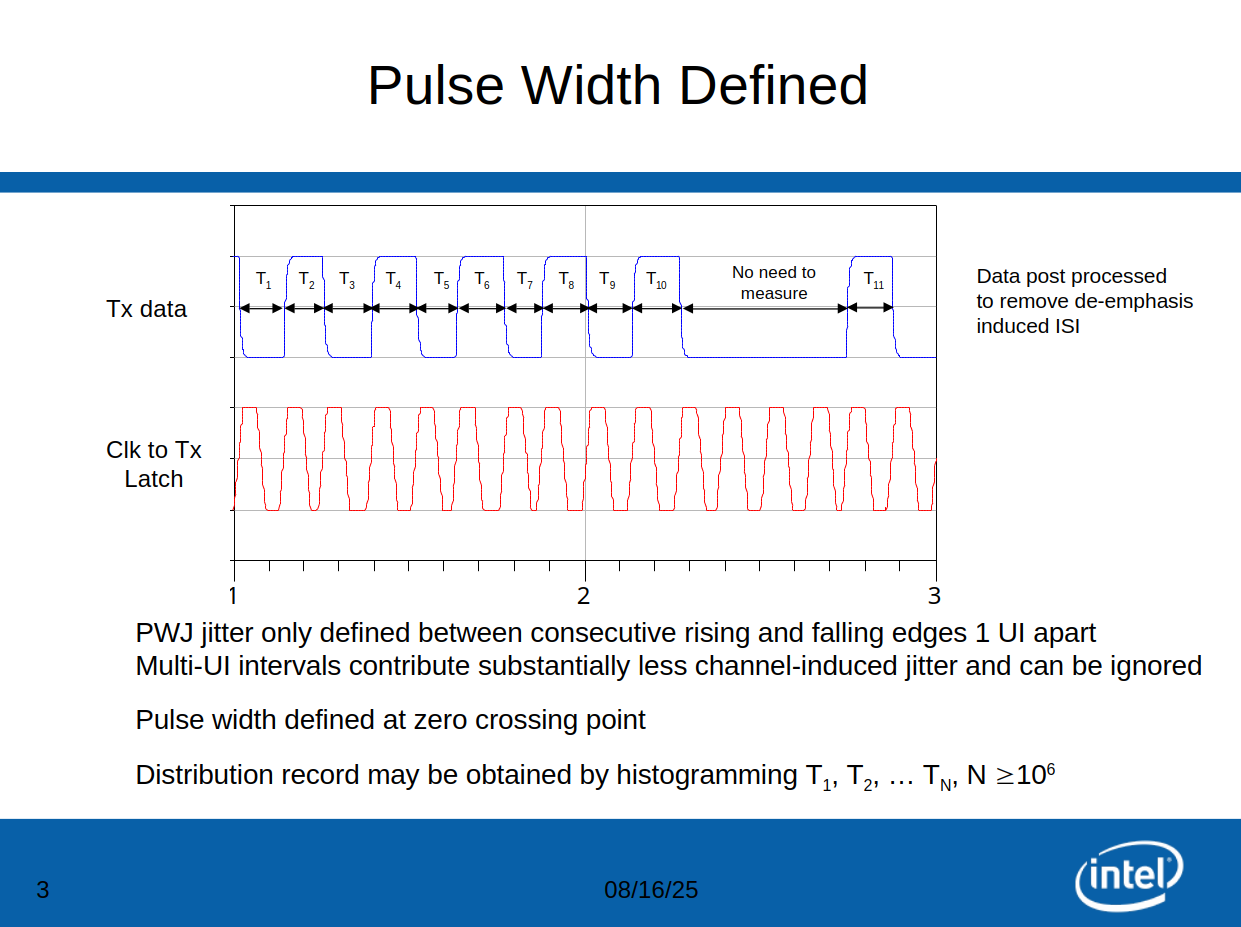
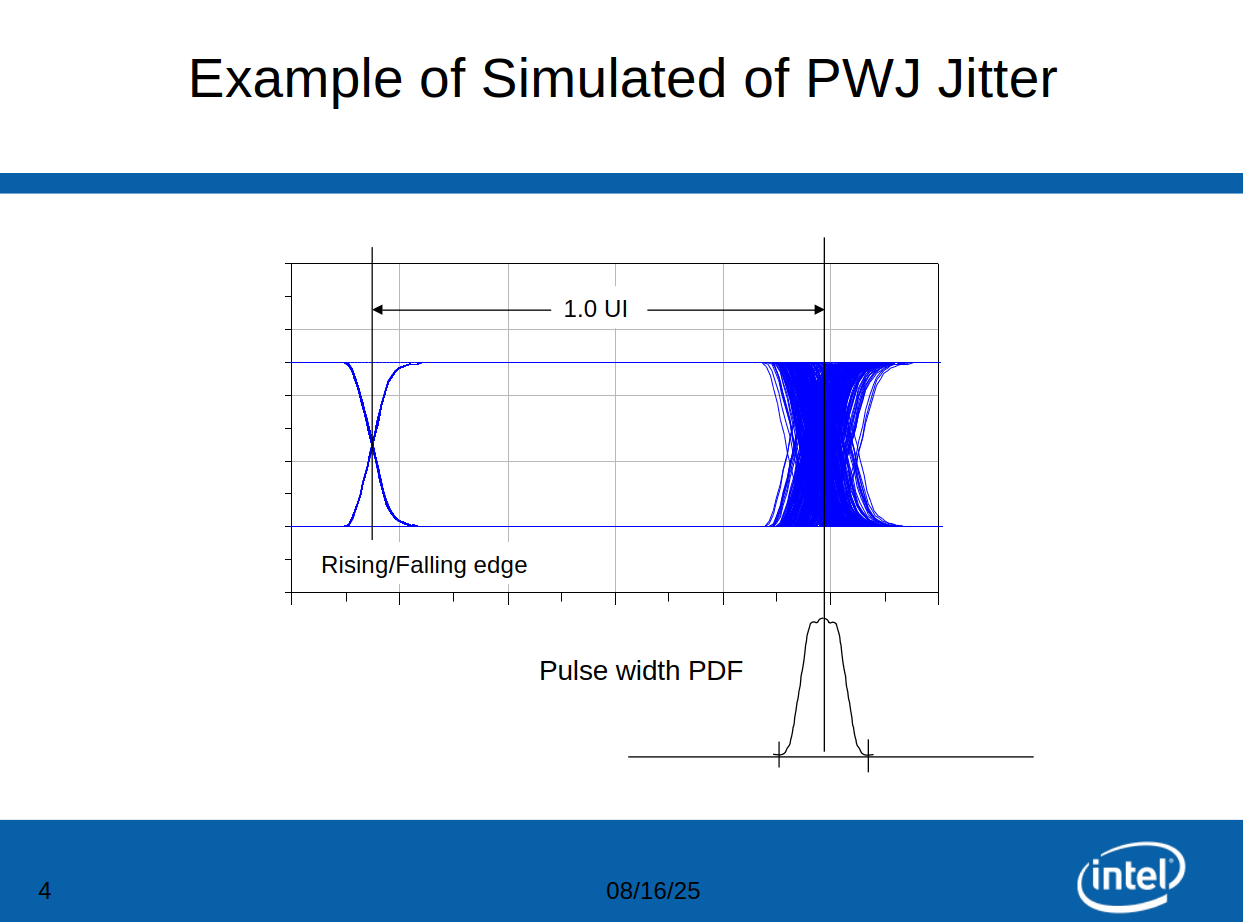
Jeff Morriss Updated 10/25/07. Analysis of 8G PCIe Pulse Width Jitter (UI to UI Jitter_10_25.ppt)
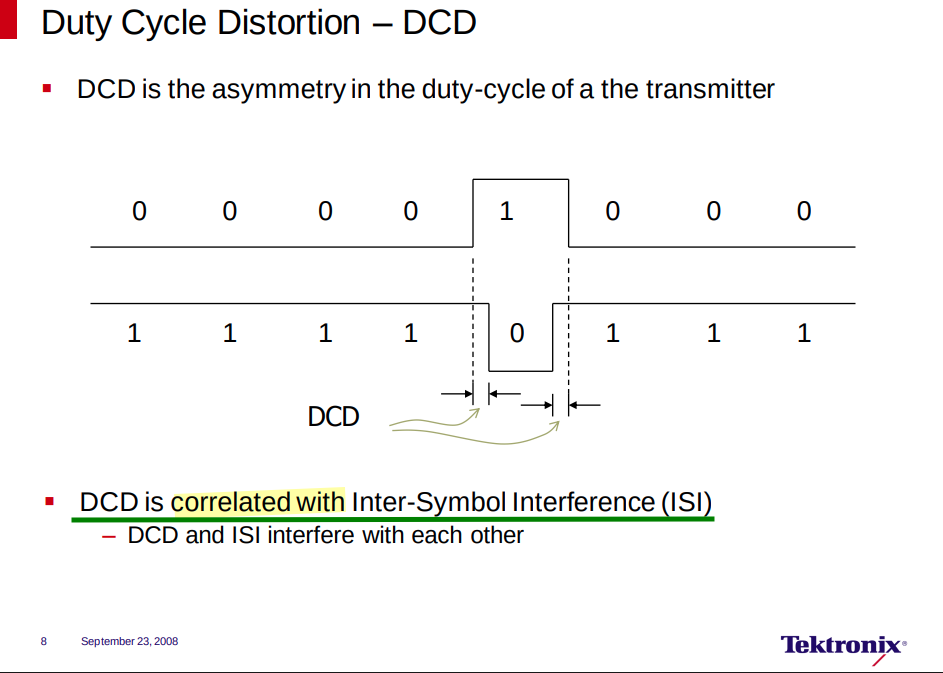
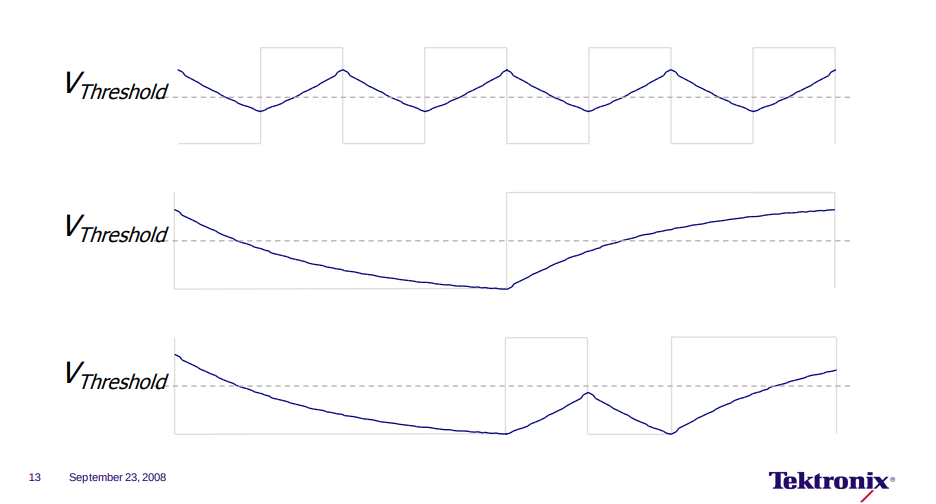
Duty Cycle Distortion – DCD
| Jitter measurement | Description |
|---|---|
| DCD | Duty Cycle Distortion is the peak-to-peak amplitude of the component of the deterministic jitter correlated with the signal polarity. |

Jitter fundamental & How Isolating Root Causes of Jitter [https://picture.iczhiku.com/resource/eetop/ShKgzTEiUfdFOcvn.pdf]
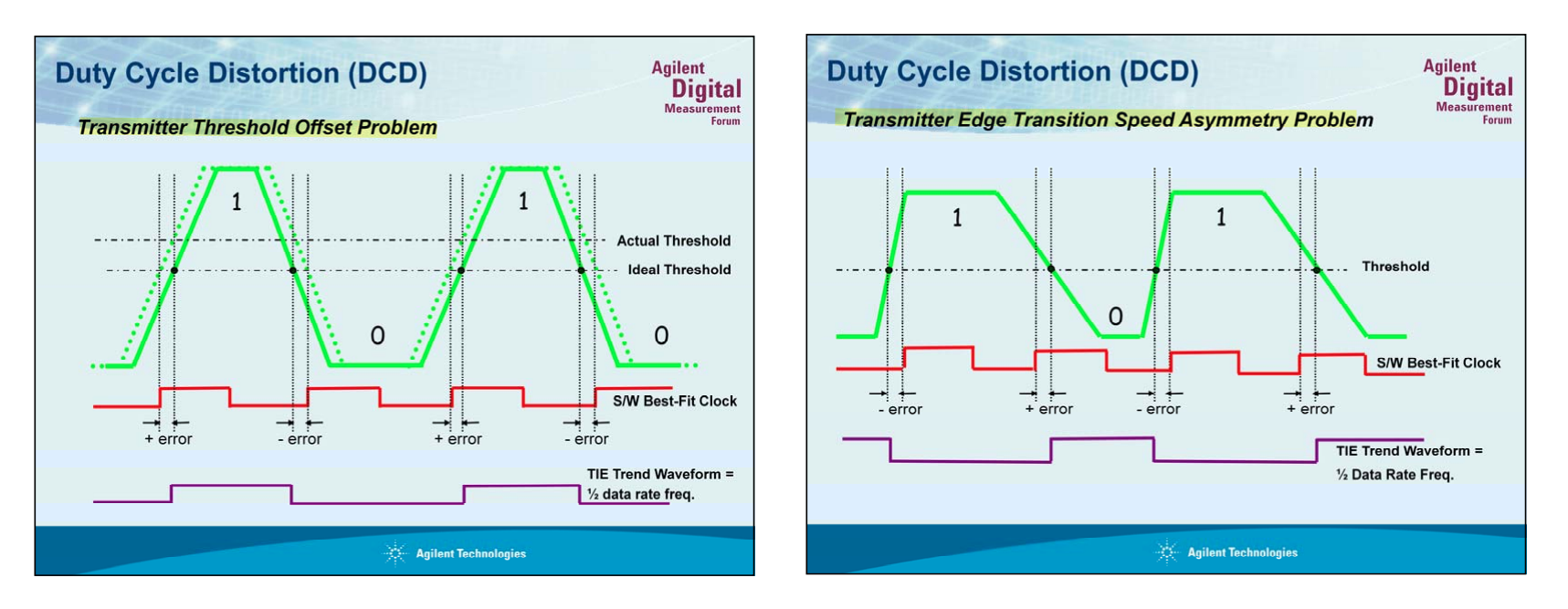
There are two primary causes of DCD jitter which are usually generated within a transmitter
- If the data input to a transmitter is theoretically perfect, but if the transmitter sampling threshold is offset from its ideal level, then the output of transmitter will have duty cycle distortion as a function of the slew rate of the data signal
- Another cause of duty cycle distortion can be a mismatch/asymmetry in rising and falling edge speeds
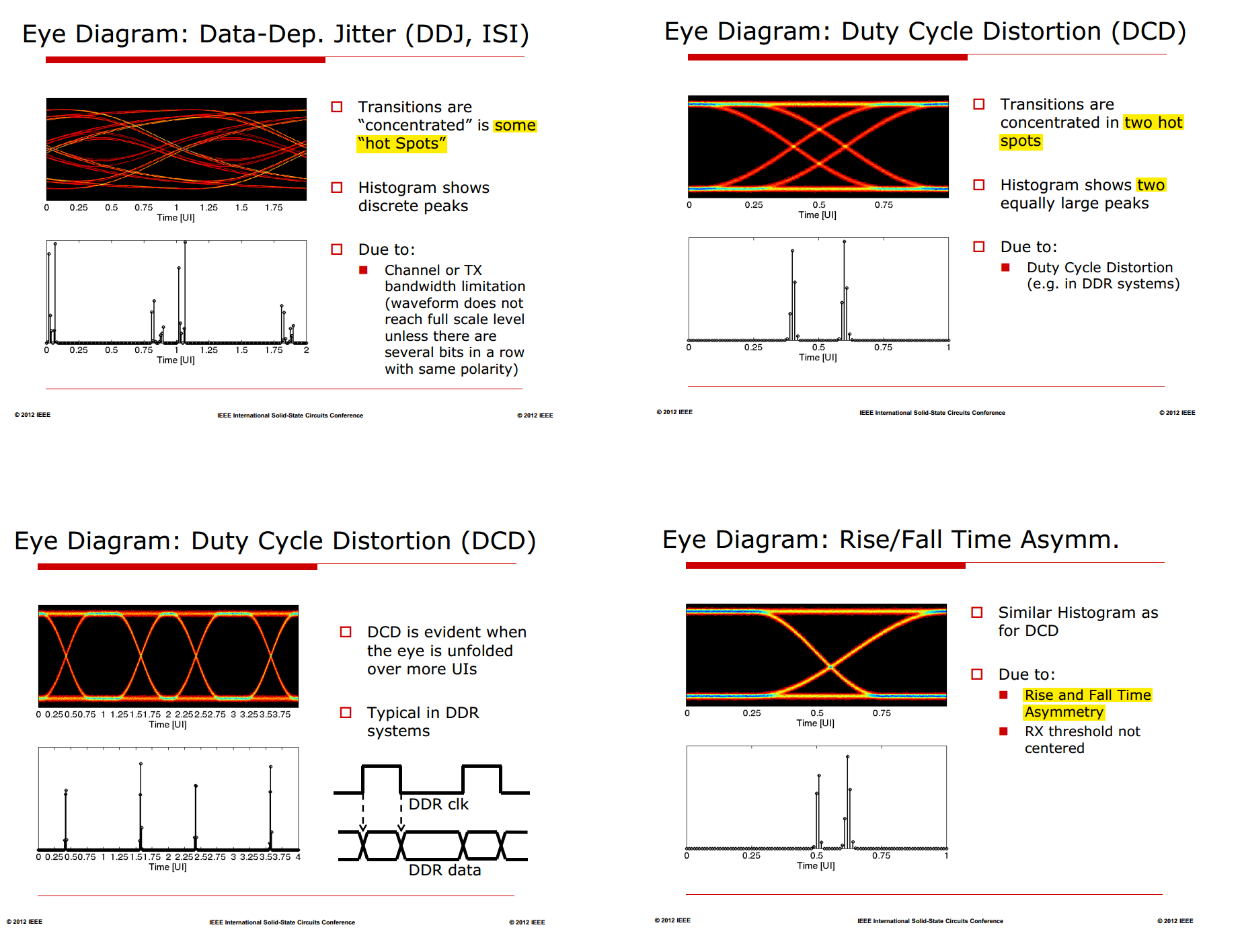
Unfortunately, other sources such as ISI almost always exist making
it sometimes difficult to isolate the DCD component. One technique to
test for DCD is to stimulate your system/components with a
repeating 1-0-1-0… data pattern. This
technique will eliminate inter-symbol interference (ISI) jitter and make
viewing the DCD within the spectrum display much easier
Why clock pattern? That's because all symbols experience same inter-symbol interference, which are canceled out
Correlated vs. Uncorrelated
If the PDF of one jitter source changes when the PDF of another source is changed, then those two sources are dependent or correlated

Inter-Symbol Interference (ISI)
The primary cause of Data Dependent Jitter

Jitter measurements can be classified into three categories: cycle-to-cycle jitter, period jitter, and long-term jitter
Jitter is a key performance parameter. Need to know what matters in each case:
- PJ for digital timing
- LTJ for data converters and serial data
- Phase noise for communications (not all bandwidths matter)
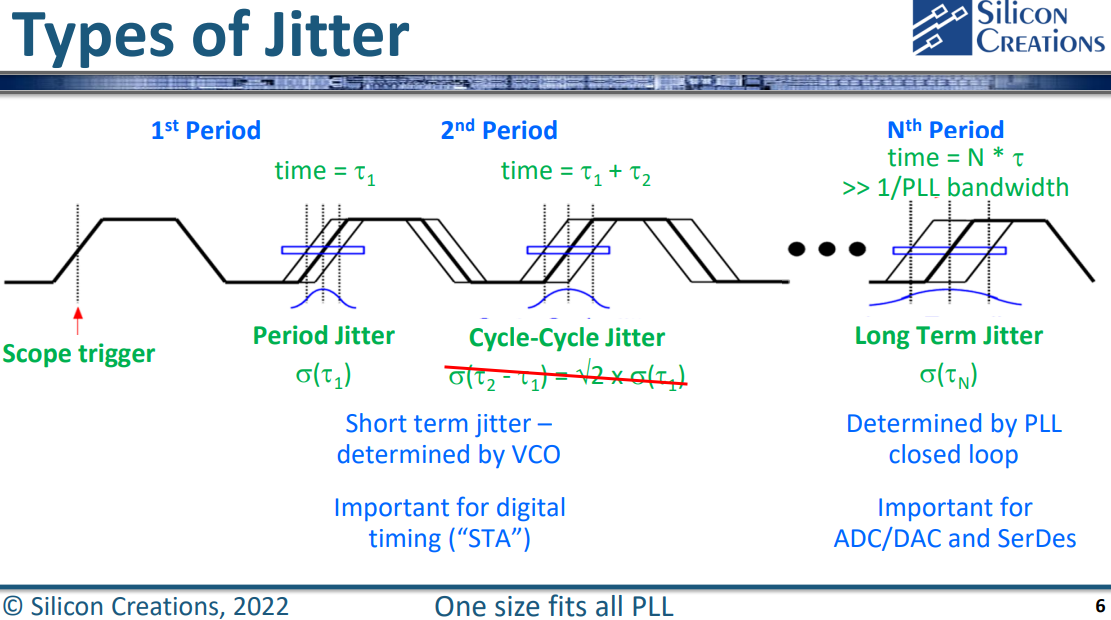
The above Cycle-Cycle Jitter equation is wrong, \(\tau_1\) and \(\tau_2\) are not independent
Short Term Jitter

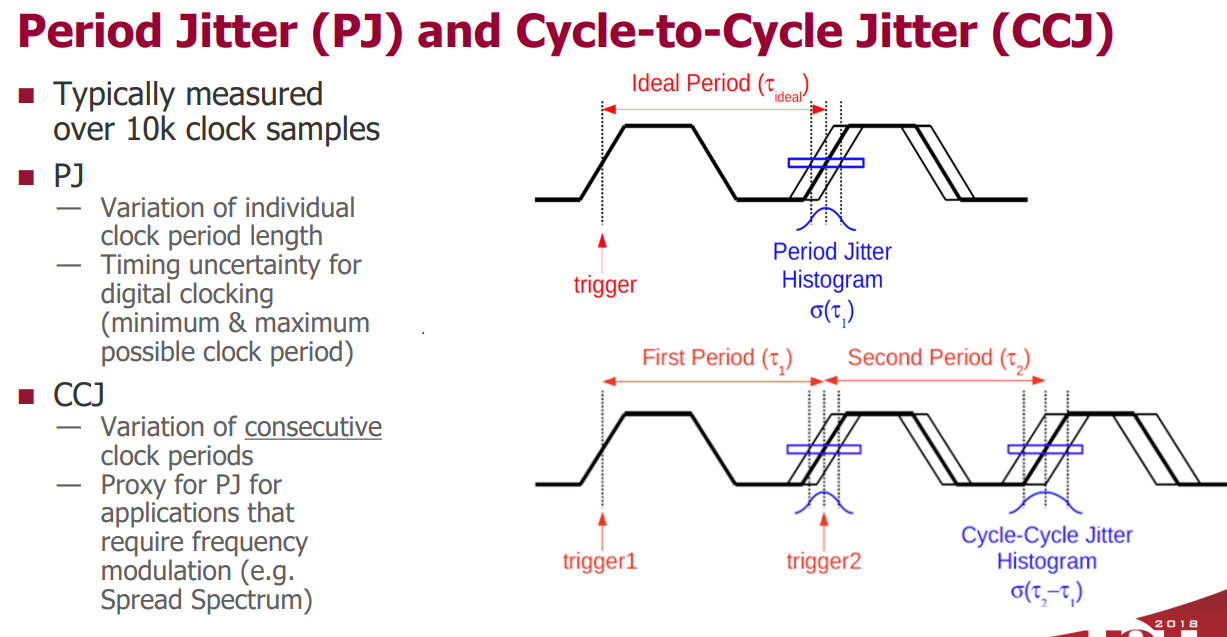
Period jitter, Jper is the short term variation in clock period compared to the average (mean) clock period.
Cycle-to-Cycle, Jcc is the time difference of two adjacent clock periods
Long Term Jitter (LTJ)
[https://people.engr.tamu.edu/spalermo/ecen689/PRBS_&_PLL_model.pdf]
absolute jitter is also known as long-term jitter

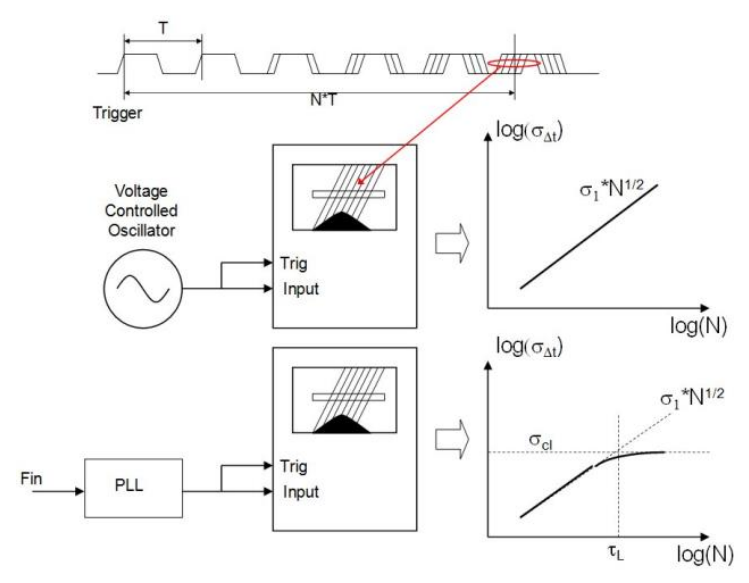
measuring LTJ

Jitter Calculation Examples
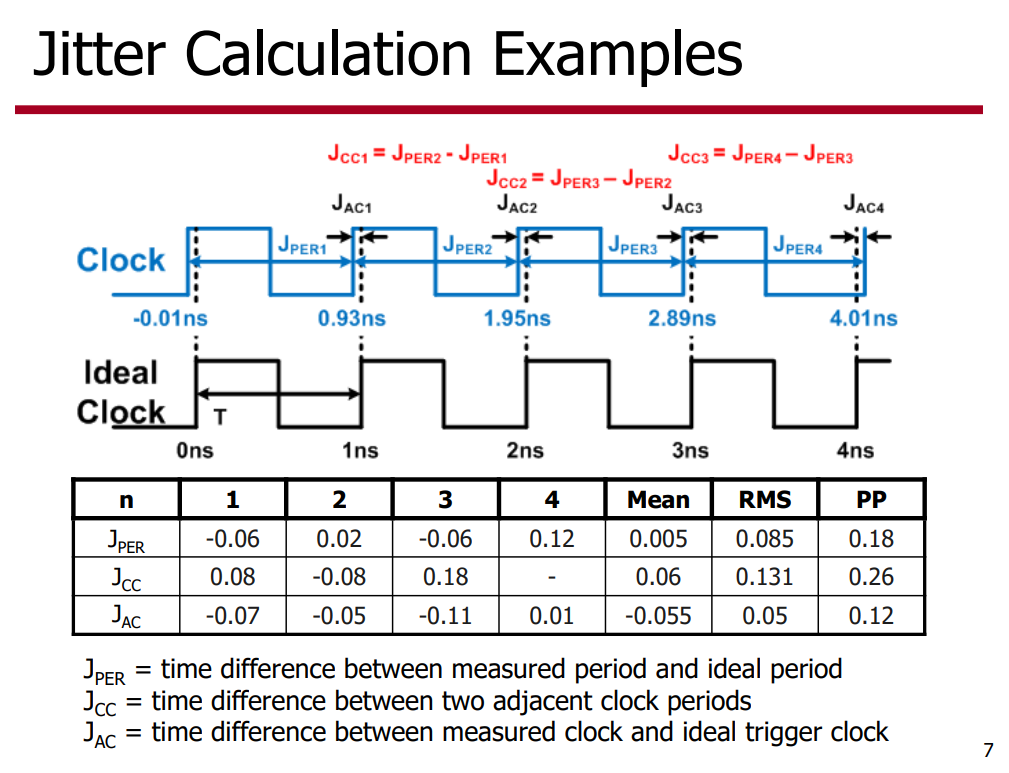
Jcc vs Jper
Estimating the RMS cycle-to-cycle jitter if all you have available is the RMS period jitter.
- Cycle-to-cycle jitter - The short-term variation in clock period between adjacent clock cycles. This jitter measure, abbreviated here as \(J_{CC}\), may be specified as either an RMS or peak-to-peak quantity.
- Period jitter - The short-term variation in clock period over all measured clock cycles, compared to the average clock period. This jitter measure, abbreviated here as \(J_{PER}\), may be specified as either an RMS or peak-to-peak quantity.
Let the variable below represent the variance of a single edge's timing jitter, i.e. the difference in time of a jittery edge versus an ideal edge, \(\sigma^2_j\)
If each edge's jitter is independent then the variance of the period jitter can be written as \[\begin{align} \sigma^2_\text{jper} &= (\sigma_\text{j(n+1)}-\sigma_\text{j(n)})^2 \\ &= \sigma_\text{j(n+1)}^2-2\sigma_\text{j(n+1)}\sigma_\text{j(n)})+\sigma_\text{j(n)})^2\\ &= \sigma_\text{j(n+1)}^2+\sigma_\text{j(n)})^2 \\ &=2\sigma^2_j \end{align}\]
In every cycle-to-cycle measurement we use one "interior" clock edge twice and therefore we must account for this
\[\begin{align} \sigma^2_\text{jcc} &= (\sigma_\text{jper(n+1)}-\sigma_\text{jper(n)})^2 \\ &=(\sigma_\text{j(n+2)}-2\sigma_\text{j(n+1)}+\sigma_\text{j(n)})^2 \end{align}\]
Since each edge's jitter is assumed to be independent and have the same statistical properties we can drop the cross correlation terms and write:
\[\begin{align} \sigma^2_\text{jcc} &=(\sigma_\text{j(n+2)}-2\sigma_\text{j(n+1)}+\sigma_\text{j(n)})^2 \\ &=\sigma_\text{j(n+2)}^2+4\sigma_\text{j(n+1)}^2+\sigma_\text{j(n)}^2 \\ &=6\sigma_\text{j}^2 \end{align}\]
The ratio of the variances is therefore \[ \frac{\sigma^2_\text{jcc}}{\sigma^2_\text{jper}} = \frac{6\sigma_\text{j}^2} {2\sigma_\text{j}^2}=3 \] Then \[ \sigma_\text{jcc} = \sqrt{3}\sigma_\text{per} \]
[Timing 101 #8: The Case of the Cycle-to-Cycle Jitter Rule of Thumb, Silicon Labs]
references
AN10007 Clock Jitter Definitions and Measurement Methods, SiTime [pdf]
SERDES Design and Simulation Using the Analog FastSPICE Platform, Silicon Creations [pdf]
Flexible clocking solutions in advanced processes from 180nm to 5nm, Silicon Creations [pdf]
One-size-fits-all PLLs for Advanced Samsung Foundry Processes, Silicon Creations [pdf]
Circuit Design and Verification of 7nm LowPower, Low-Jitter PLLs, Silicon Creations, [pdf]
Lecture 10: Jitter, ECEN720: High-Speed Links Circuits and Systems Spring 2023 [pdf]
Jitter 360° Knowledge Series [pdf, slides]
N. Da Dalt, "Tutorial: Jitter: Basic and Advanced Concepts, Statistics, and Applications," 2012 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 2012 [slides, transcript ]

