Single-Bit Response (SBR) & Double-Edge Response (DER)
Three fast time-domain system simulation techniques:
- single-bit response method
- double-edge response method
- multiple-edge response method
Single-Bit Response (SBR) Method
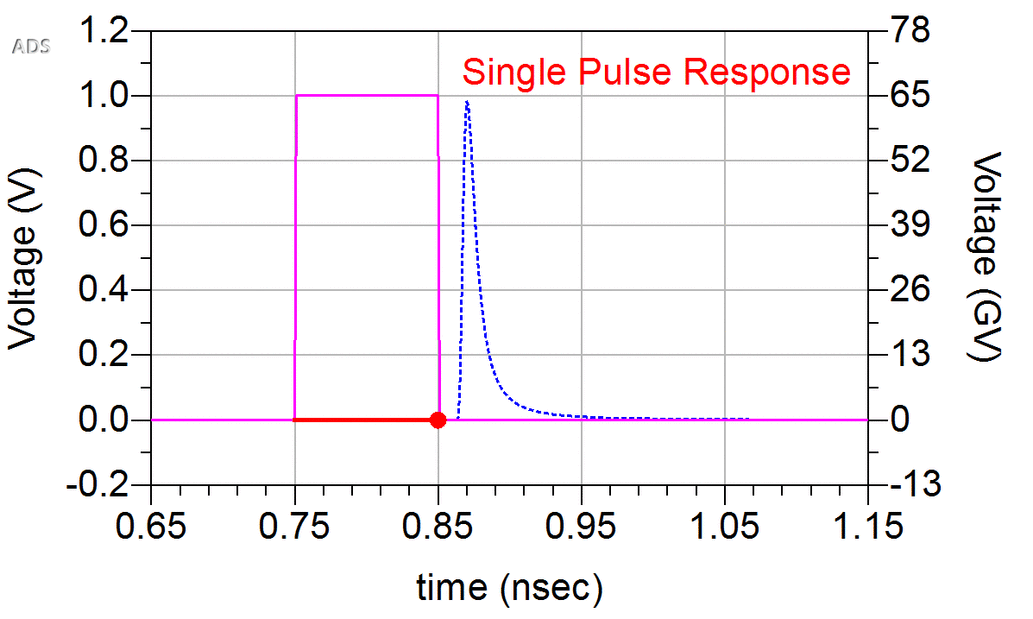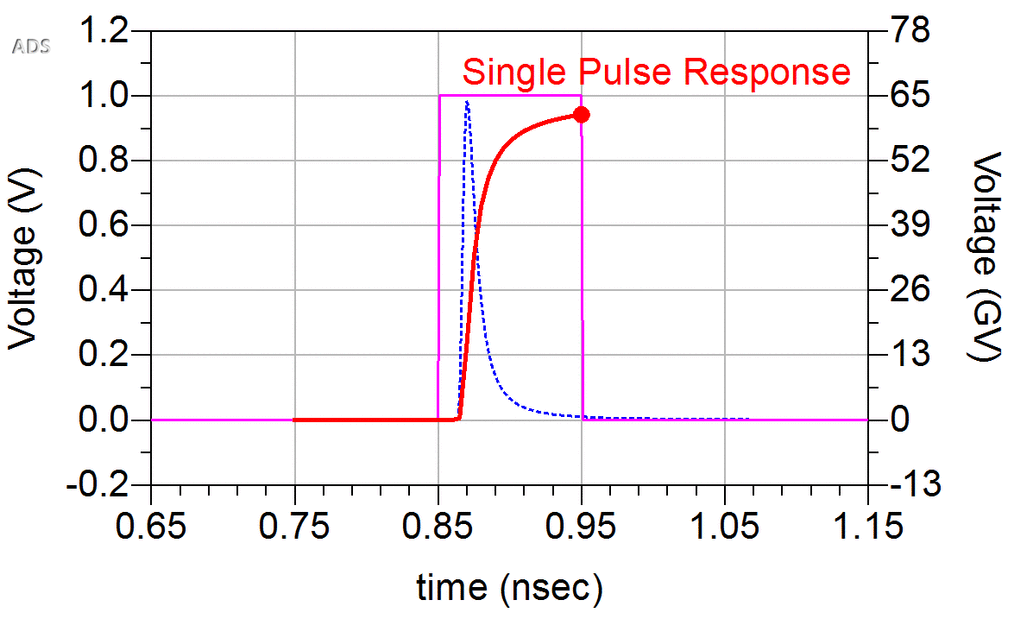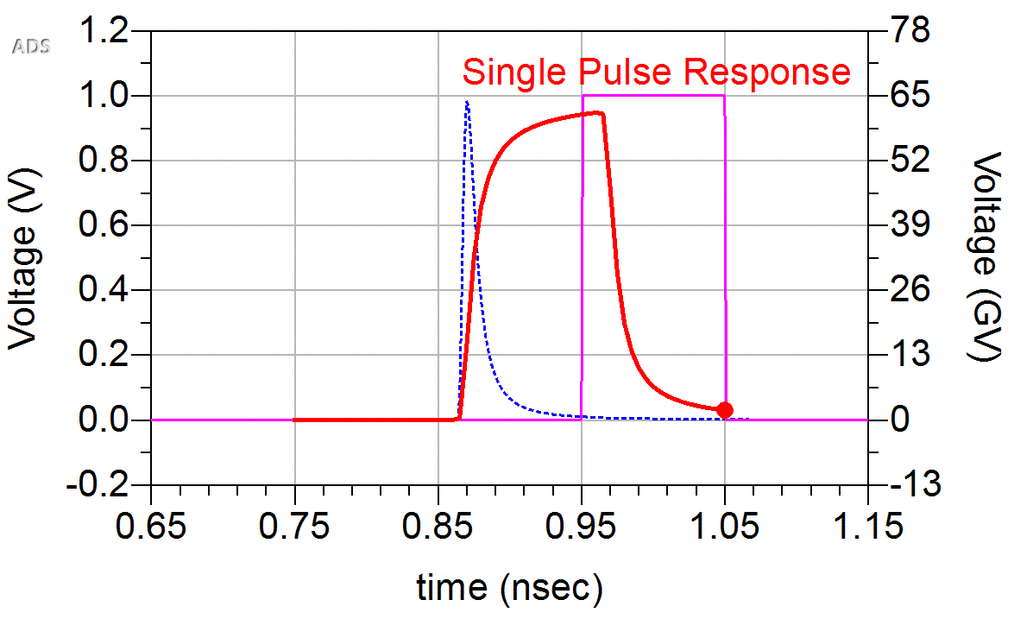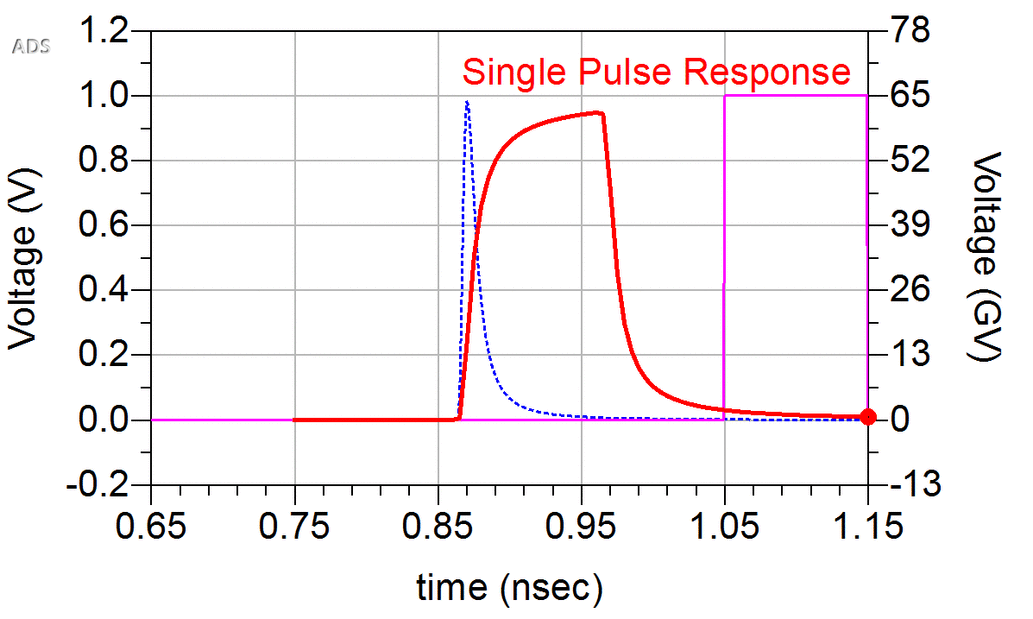
Overlapping portions of a pulse response from neighboring bits are referred to as intersymbol interference (ISI). A received waveform is formed by superimposing, in time, the pulse responses of each bit in the sequence, as illustrated in Figure 9, assuming symmetric positive and negative pulses are transmitted for 1s and 0s
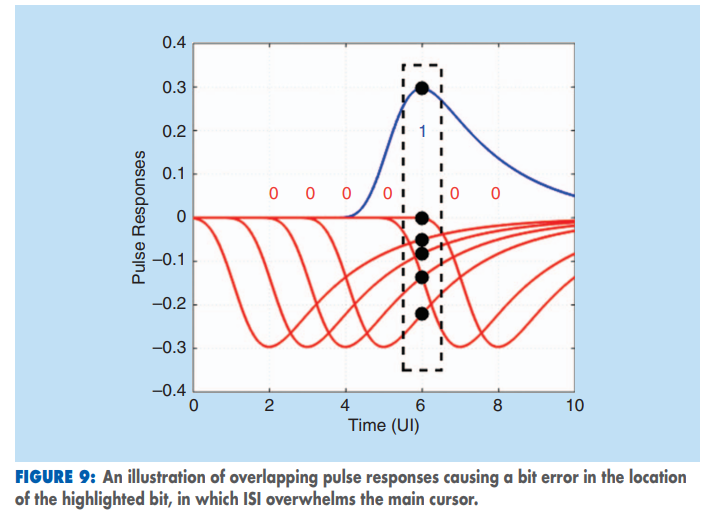
To avoid spurious glitches between consecutive ones, rising and falling edge responses shall be symmetric. This is the limitation of SBR method.
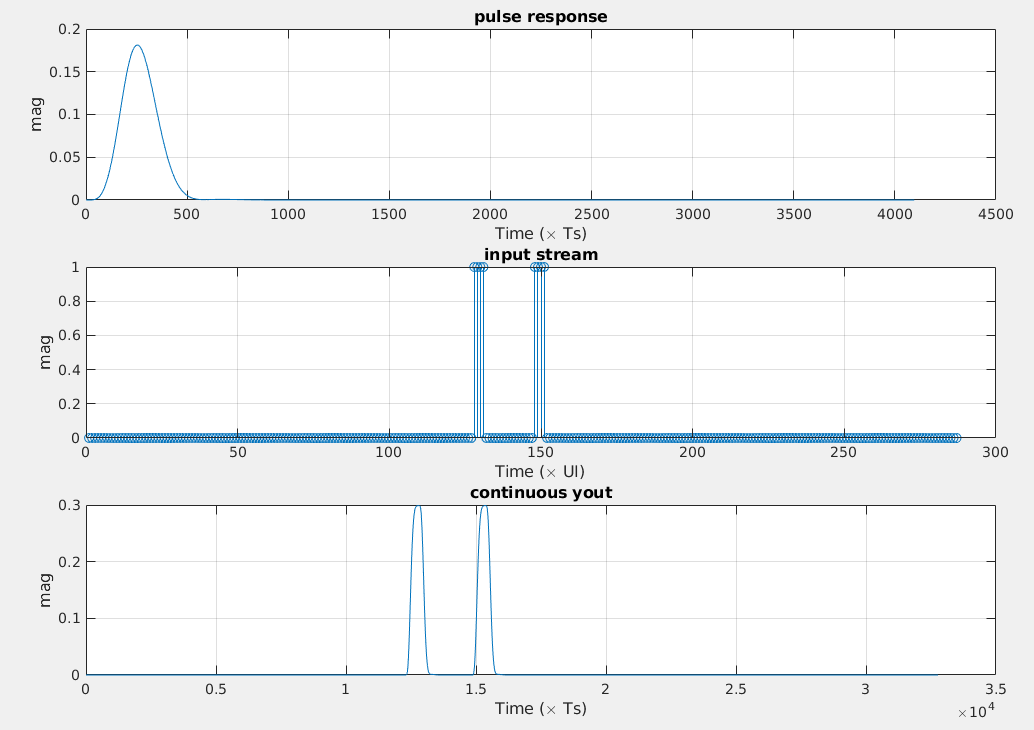
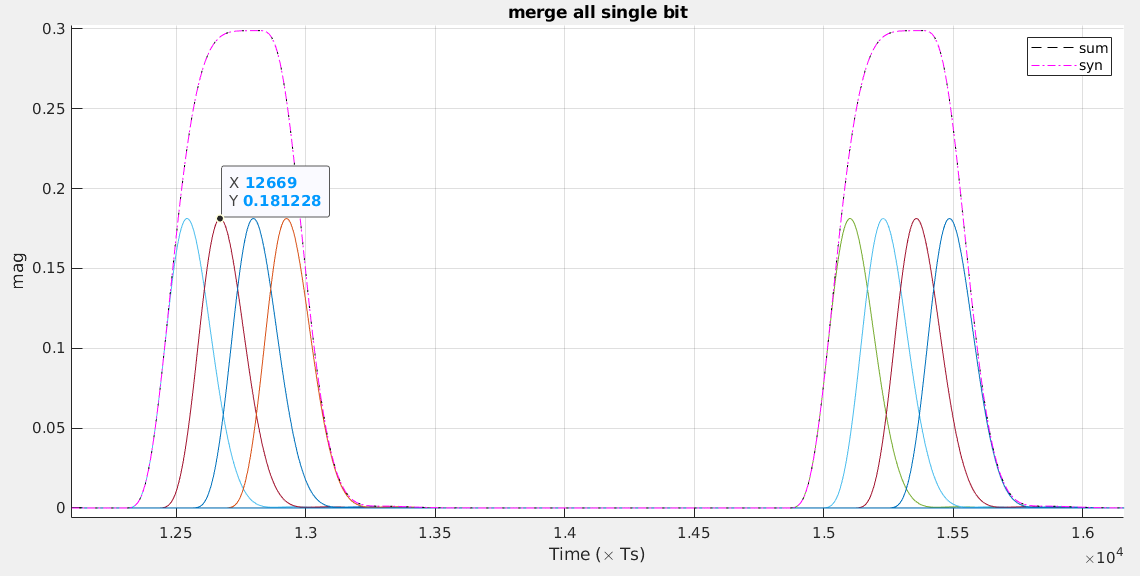
Let \(p(t)\) be the SBR of the channel, \(t_s\) be the data sampling phase, \(T\) be the bit time, \(N_c\) is the number of UI in stored pulse response and \(b_m\) be the \(m\)th transmitted symbol. The voltage seen by the receiver's data sampler at the \(m\)th data sample is determined by \[ y_m = \sum_{k=m-N_c+1}^{m}b_kp(t_s+(m-k)T) \] where \(b_k \in [0, 1]\) and \(p(t) \ge 0\)
We always prepend \(Nc-1\) 0s in random bit stream for consistency.
For computation convenient, the pulse need to be positive. For differential signal and amplitude \(V_{peak}\), the peak to peak is \(-V_{peak}\) to \(+V_{peak}\). After pulse added by \(V_{peak}\), peak to peak is \(0\) to \(+2V_{peak}\).
1 | hold on; |
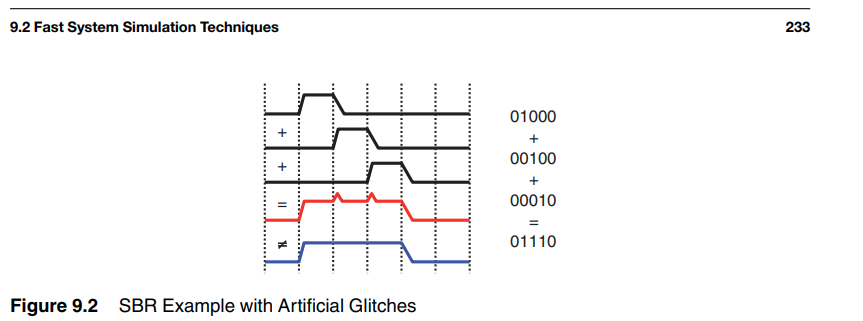
The pulse response contain rising and falling edge. The 1 bit first rise from -1 to 1, then fall to -1; The 0 bit just do nothing for synthesized waveform with the help of falling edge of 1 bit.
The DC shift help deal with continuous 0 bits.
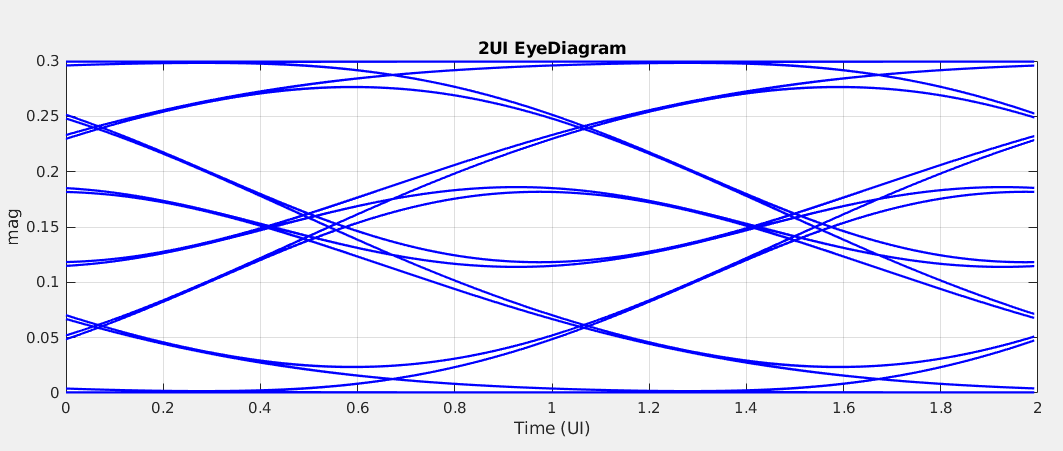
another SBR example
1 | A = zeros(10,21); |
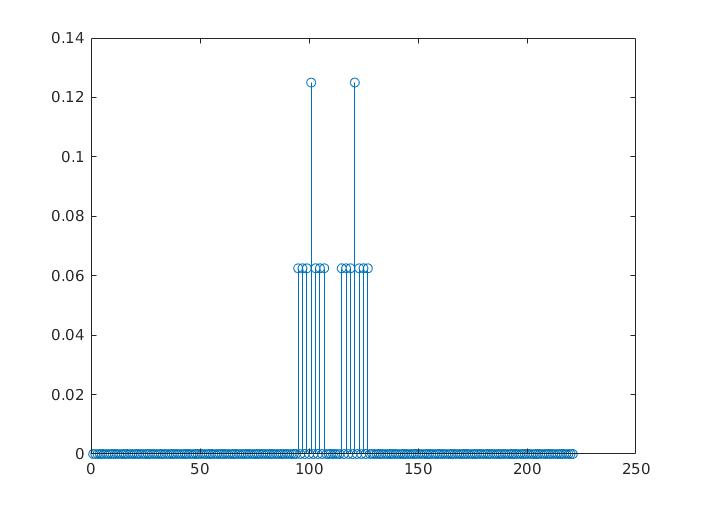
S-Parameter to Single Bit Response (SBR)
Mike Li, "S-Parameter to Single Bit Response (SBR) Transformation and Convergence Study" [https://ieee802.org/3/bj/public/may12/li_01_0512.pdf]
TODO 📅
Double-Edge Response (DER) Method
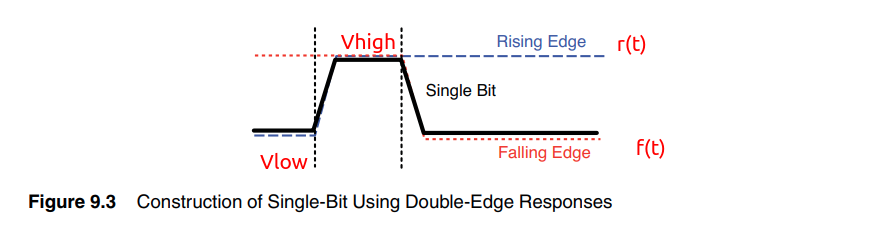
To handle the more general cases, with asymmetric rising and falling edges, the system response can be constructed in terms of edge transitions instead of bit responses.
The DER method decomposes the input data pattern, in terms of rising and falling edge transitions. The system response can be calculated by superimposing the shifted versions of the rising and falling edge responses : \[ y_m = \sum_{k=m-N_c+1}^{m}(b_k-b_{k-1})s_k(t_s+(m-k)T) + y_{int} \] where
\[\begin{align} s_i(t) &= r(t) -V_{low} \quad \text{if} \: (b_i\gt b_{i-1}) \\ &= V_{high}-f(t) \quad \text{otherwise} \end{align}\]
\(r(t)\) and \(f(t)\) are the rising and falling edge responses,respectively. \(V_{high}\) and \(V_{low}\) are the steady state DC levels, in response to a constant stream of ones and zeros, respectively. \(y_{int}\) is the initial DC state (either \(V_{high}\) or \(V_{low}\) ).
We always prepend \(Nc\) 0s in random bit stream for consistency.
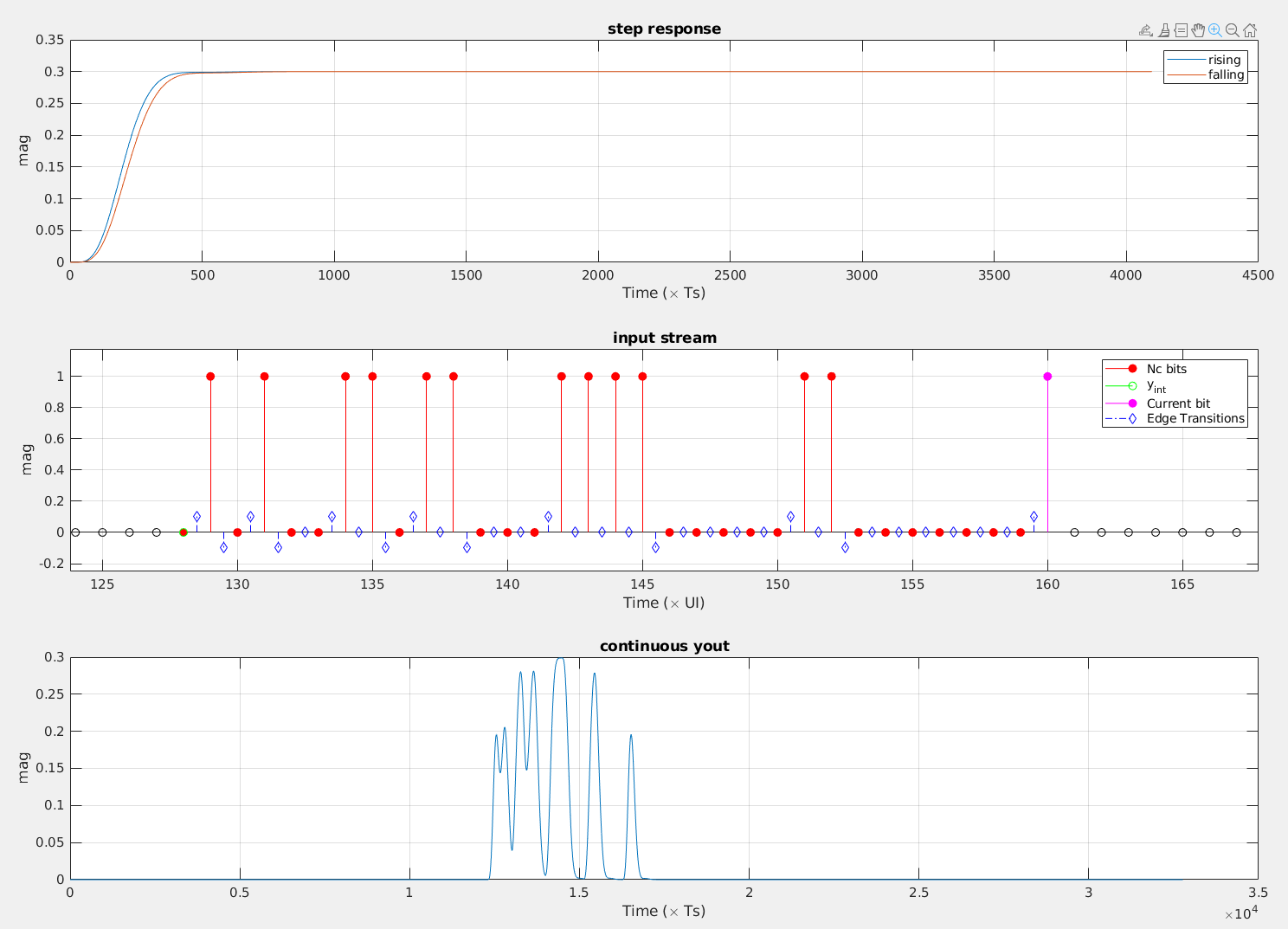
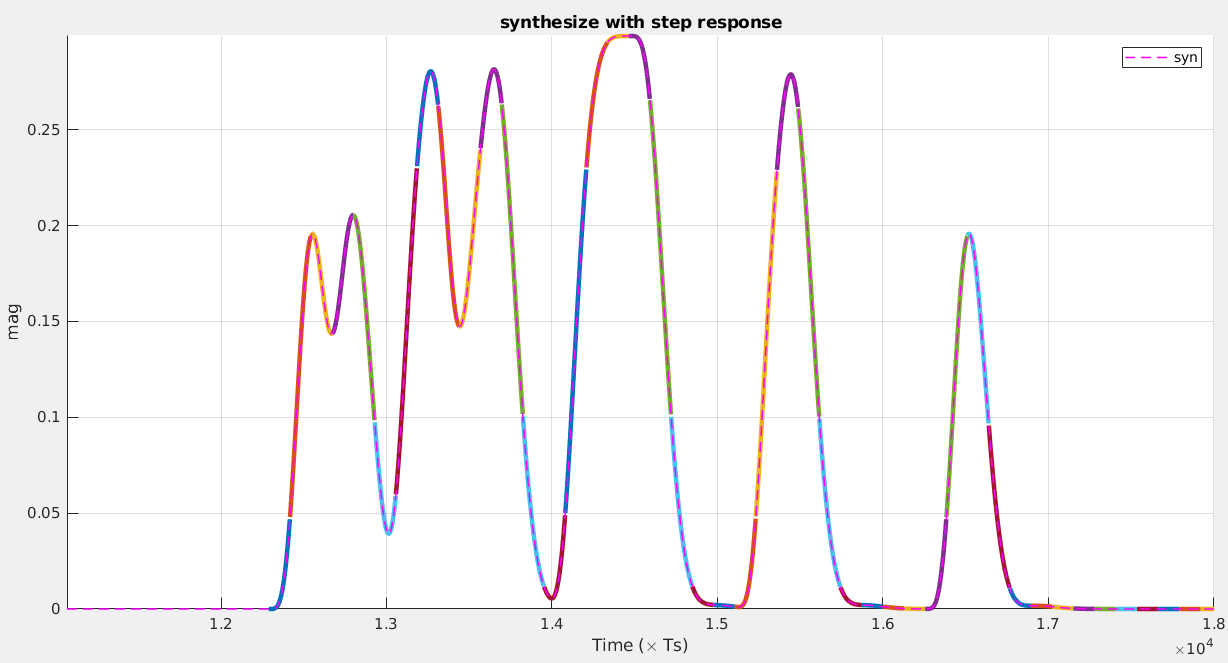
1 | figure(1) |
Reference
T. C. Carusone, "Introduction to Digital I/O: Constraining I/O Power Consumption in High-Performance Systems," in IEEE Solid-State Circuits Magazine, vol. 7, no. 4, pp. 14-22, Fall 2015
Oh, Kyung Suk Dan, and Xing Chao Chuck Yuan. High-Speed Signaling: Jitter Modeling, Analysis, and Budgeting. Prentice Hall, 2011.
Ren, Jihong and Kyung Suk Oh. “Multiple Edge Responses for Fast and Accurate System Simulations.” IEEE Transactions on Advanced Packaging 31 (2008): 741-748.
Shi, Rui. “Off-chip wire distribution and signal analysis.” (2008).
X. Chu, W. Guo, J. Wang, F. Wu, Y. Luo and Y. Li, "Fast and Accurate Estimation of Statistical Eye Diagram for Nonlinear High-Speed Links," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 29, no. 7, pp. 1370-1378, July 2021, doi: 10.1109/TVLSI.2021.3082208.