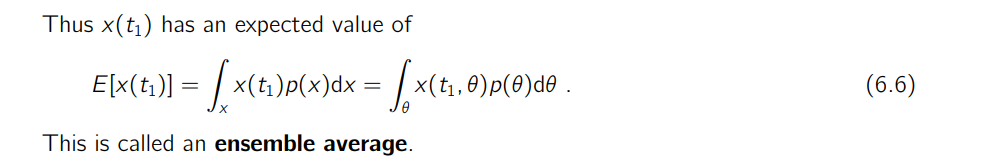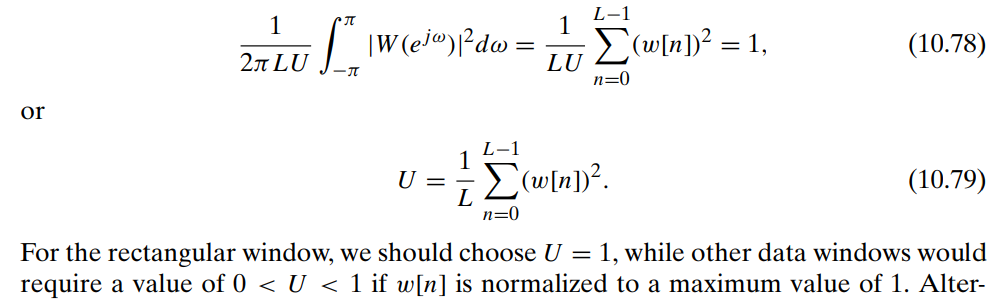Random Process

Posted on Edited on In

image-20241106231114717

autocorrelation

image-20241116112504606

The expectation returns the probability-weighted average of the specific function at that specific time over all possible realizations of the process

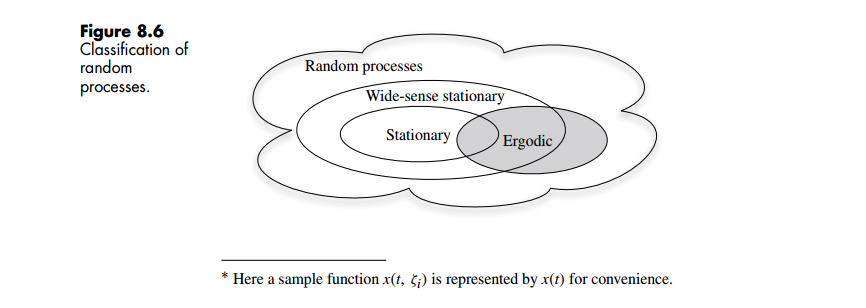
Ergodicity

ensemble autocorrelation and temporal autocorrelation (time autocorrelation)

image-20240719230346944

image-20240719210621021

image-20241123004051314

ECE438 - Laboratory 7: Discrete-Time Random Processes (Week 2) October 6, 2010 [https://engineering.purdue.edu/VISE/ee438L/lab7/pdf/lab7b.pdf]

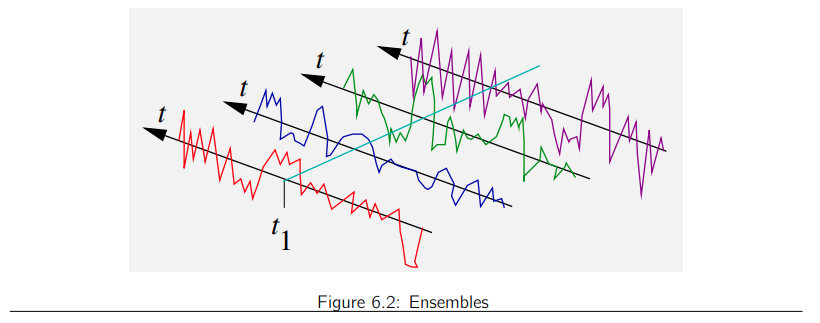
Ensemble Averages and Time Averages

[https://ece-research.unm.edu/bsanthan/ece541/stat.pdf]

[https://www.nii.ac.jp/qis/first-quantum/e/forStudents/lecture/pdf/noise/chapter1.pdf]

  • time average: time-averaged quantities for the \(i\)-th member of the ensemble
  • ensemble average: ensemble-averaged quantities for all members of the ensemble at a certain time

image-20241116113758119

image-20241116215119239

image-20241116215140298

where \(\theta\) is one member of the ensemble; \(p(x)dx\) is the probability that \(x\) is found among \([x, x + dx]\)

sample autocorrelation

[https://engineering.purdue.edu/VISE/ee438L/lab7/pdf/lab7b.pdf]

image-20250912203526260

[http://www.signal.uu.se/Courses/CourseDirs/SignalbehandlingIT/forelas02.pdf]

image-20250912205534933

ergodic vs. stationary

[https://bookdown.org/kevin_davisross/stat350-handouts/stationary.html]

image-20250912211619068

image-20250912211353183

Strict Sense Stationary (SSS) & Wide Sense Stationary (WSS)

[https://ece-research.unm.edu/bsanthan/ece541/station.pdf]

image-20250912210738010

image-20241123221623537

image-20240720140527704

LTI Filtering of WSS process

mean

image-20240917104857284

image-20240917104916086

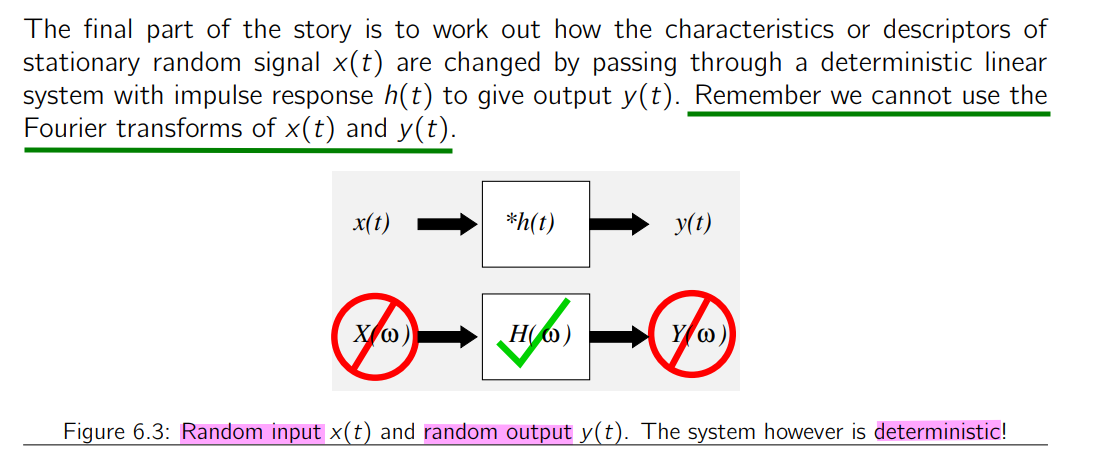
image-20240827221945277

autocorrelation

deterministic autocorrelation function

image-20240427170024123

\[ R_{yy}(\tau) = h(\tau)*R_{xx}(\tau)*h(-\tau) =R_{xx}(\tau)*h(\tau)*h(-\tau) \]

image-20240907211343832

why \(\overline{R}_{hh}(\tau) \overset{\Delta}{=} h(\tau)*h(-\tau)\) is autocorrelation ? the proof is as follows:

\[\begin{align} \overline{R}_{hh}(\tau) &= h(\tau)*h(-\tau) \\ &= \int_{-\infty}^{\infty}h(x)h(-(\tau - x))dx \\ &= \int_{-\infty}^{\infty}h(x)h(-\tau + x)dx \\ &=\int_{-\infty}^{\infty}h(x+\tau)h(x)dx \end{align}\]

PSD

image-20240827222224395

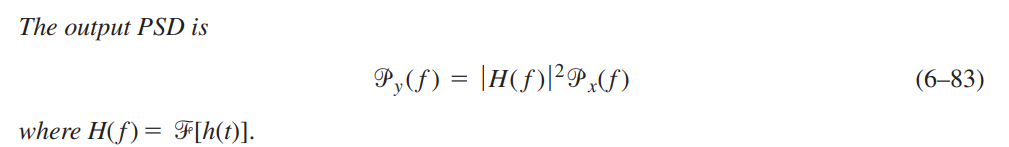
image-20240827222235906

Topic 6 Random Processes and Signals [https://www.robots.ox.ac.uk/~dwm/Courses/2TF_2021/N6.pdf]

Alan V. Oppenheim, Introduction To Communication, Control, And Signal Processing [https://ocw.mit.edu/courses/6-011-introduction-to-communication-control-and-signal-processing-spring-2010/a6bddaee5966f6e73450e6fe79ab0566_MIT6_011S10_notes.pdf]

Balu Santhanam, Probability Theory & Stochastic Process 2020: LTI Systems and Random Signals [https://ece-research.unm.edu/bsanthan/ece541/LTI.pdf]

Time Reversal \[ x(-t) \overset{FT}{\longrightarrow} X(-j\omega) \]

if \(x(t)\) is real, then \(X(j\omega)\)​ has conjugate symmetry \[ X(-j\omega) = X^*(j\omega) \]

Derivatives of Random Processes

since \(x(t)\) is stationary process, and \(y(t) = \frac{dx(t)}{dt}\)

Using \(R_{yy}(\tau) = h(\tau)*R_{xx}(\tau)*h(-\tau)\)

\[\begin{align} R_{yy}(\tau) &= \mathcal{F}^{-1}[H(j\omega)\Phi_{xx}(j\omega)H(-j\omega)] \\ &= \mathcal{F}^{-1}[-(j\omega)^2\Phi_{xx}(j\omega)] \end{align}\]

we obtain the autocorrelation function of the output process as \[ R_{yy}(\tau) = -\frac{d^2}{d\tau^2}R_{xx}(\tau) \]

Liu Congfeng, Xidian University. Random Signal Processing: Chapter 5 Linear System: Random Process [https://web.xidian.edu.cn/cfliu/files/20121125_153218.pdf]

[https://sharif.ir/~bahram/sp4cl/PapoulisLectureSlides/lectr14.pdf]

Periodogram

The periodogram is in fact the Fourier transform of the aperiodic correlation of the windowed data sequence

image-20240907215822425

image-20240907215957865

image-20240907230715637

estimating continuous-time stationary random signal

periodogram.drawio

The sequence \(x[n]\) is typically multiplied by a finite-duration window \(w[n]\), since the input to the DFT must be of finite duration. This produces the finite-length sequence \(v[n] = w[n]x[n]\)

image-20240910005608007

image-20240910005927534

image-20240910005723458

\[\begin{align} \hat{P}_{ss}(\Omega) &= \frac{|V(e^{j\omega})|^2}{LU} \\ &= \frac{|V(e^{j\omega})|^2}{\sum_{n=0}^{L-1}(w[n])^2} \tag{1}\\ &= \frac{L|V(e^{j\omega})|^2}{\sum_{k=0}^{L-1}(W[k])^2} \tag{2} \end{align}\]

image-20240910010638376

That is, by \((1)\) \[ \hat{P}_{ss}(\Omega) = T_s\hat{P}_{xx(\omega)} = \frac{T_s|V(e^{j\omega})|^2}{\sum_{n=0}^{L-1}(w[n])^2}=\frac{|V(e^{j\omega})|^2}{f_{res}L\sum_{n=0}^{L-1}(w[n])^2} \]

That is, by \((2)\) \[ \hat{P}_{ss}(\Omega) = T_s\hat{P}_{xx(\omega)} = \frac{T_sL|V(e^{j\omega})|^2}{\sum_{k=0}^{L-1}(W[k])^2} = \frac{|V(e^{j\omega})|^2}{f_{res}\sum_{k=0}^{L-1}(W[k])^2} \]

!! ENBW

Wiener-Khinchin theorem

Norbert Wiener proved this theorem for the case of a deterministic function in 1930; Aleksandr Khinchin later formulated an analogous result for stationary stochastic processes and published that probabilistic analogue in 1934. Albert Einstein explained, without proofs, the idea in a brief two-page memo in 1914

\(x(t)\), Fourier transform over a limited period of time \([-T/2, +T/2]\) , \(X_T(f) = \int_{-T/2}^{T/2}x(t)e^{-j2\pi ft}dt\)

With Parseval's theorem \[ \int_{-T/2}^{T/2}|x(t)|^2dt = \int_{-\infty}^{\infty}|X_T(f)|^2df \] So that \[ \frac{1}{T}\int_{-T/2}^{T/2}|x(t)|^2dt = \int_{-\infty}^{\infty}\frac{1}{T}|X_T(f)|^2df \]

where the quantity, \(\frac{1}{T}|X_T(f)|^2\) can be interpreted as distribution of power in the frequency domain

For each \(f\) this quantity is a random variable, since it is a function of the random process \(x(t)\)

The power spectral density (PSD) \(S_x(f )\) is defined as the limit of the expectation of the expression above, for large \(T\): \[ S_x(f) = \lim _{T\to \infty}\mathrm{E}\left[ \frac{1}{T}|X_T(f)|^2 \right] \]

The Wiener-Khinchin theorem ensures that for well-behaved wide-sense stationary processes the limit exists and is equal to the Fourier transform of the autocorrelation \[\begin{align} S_x(f) &= \int_{-\infty}^{+\infty}R_x(\tau)e^{-j2\pi f \tau}d\tau \\ R_x(\tau) &= \int_{-\infty}^{+\infty}S_x(f)e^{j2\pi f \tau}df \end{align}\]

Note: \(S_x(f)\) in Hz and inverse Fourier Transform in Hz (\(\frac{1}{2\pi}d\omega = df\))

image-20240910003805151

[https://www.robots.ox.ac.uk/~dwm/Courses/2TF_2011/2TF-L5.pdf]

Frank R. Kschischang. The Wiener-Khinchin Theorem [https://www.comm.utoronto.ca/~frank/notes/wk.pdf]

Example

image-20240904203802604

Remember: impulse scaling

image-20240718210137344 \[ \cos(2\pi f_0t) \overset{\mathcal{F}}{\longrightarrow} \frac{1}{2}[\delta(f -f_0)+\delta(f+f_0)] \]

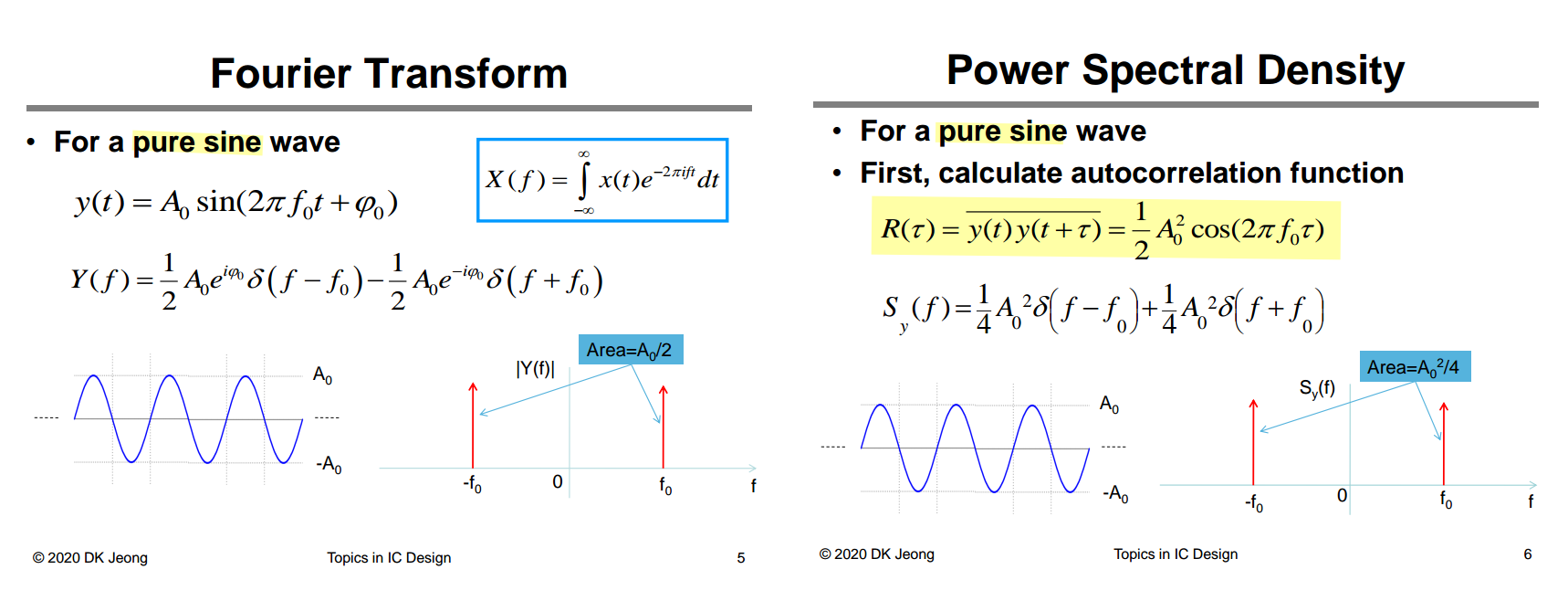
image-20250821200319537

\(x(t)\) \(R(\tau)\)
\(A_0 \sin(\omega_0 t+\phi_0)\) \(\frac{A_0^2}{2}\cos(\omega_0 \tau)\)
\(A_0 \cos(\omega_0 t+\phi_0)\) \(\frac{A_0^2}{2}\cos(\omega_0 \tau)\)

due to \(\cos(\omega_0 t +\phi_0) = \sin(\omega_0 t +\phi_0 + \frac{\pi}{2})\)

Energy Signal

image-20240910004411501

image-20240910004421791

image-20240910004448439

Discrete time

SIMG-713 Noise and Random Processes Spring 2002 . Lecture 15 Power Spectrum Estimation [https://www.cis.rit.edu/class/simg713/Lectures/Lecture713-15-4.pdf]

Properties of the Fourier Transform for Discrete-Time Signals [https://www.comm.utoronto.ca/dkundur/course_info/362/EmanHammadDTFT2.pdf]

image-20250810165917800 \[ \frac{1}{2\pi}F^{-1}\{R_{xx}\}d\omega = \frac{1}{2\pi}F^{-1}\{R_{xx}\}d(2\pi f T)=T\cdot F^{-1}\{R_{xx}\}df = P_{xx}(f)df \] power spectral density of a discrete-time random process \(\{x(n)\}\) is given by \[ P_{xx}(f) =T\cdot F^{-1}\{R_{xx}\} \]

Periodic and Cyclostationary Processes

image-20250809234136591

image-20250809234318422

Multirate Systems & Random Sequences

Balu Santhanam. ece541 Probability Theory & Stochastic Process: Random Signals and Multirate Systems [http://ece-research.unm.edu/bsanthan/ece541/rand.pdf]

WSS Random Sequences

autocorrelation function of WSS random sequences

image-20250818202413226

psd of WSS of WSS random sequences

image-20250818202138087

Interpretation of the psd

image-20250818205138125

Equation 8.4-4 is permissible for cyclostationary waveforms

decimation

image-20250810194206762

\[ \frac{1}{M}\int_{-Mx_0}^{Mx_0}f(\frac{x}{M})dx = \int_{-Mx_0}^{Mx_0}f(\frac{x}{M}) d\frac{x}{M} = \int_{-x_0}^{x_0} f(\acute{x}) d\acute{x} \]

where \(\acute{x} = \frac{x}{M}\)

randSeq-decimation.drawio

image-20250818195951584

image-20250818205826429

interpolation

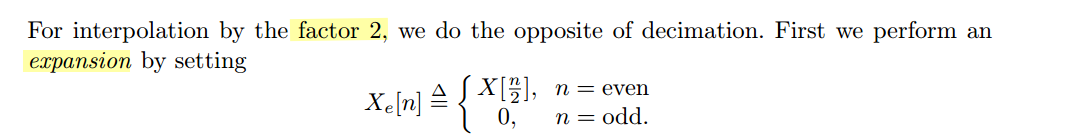
image-20250819182525306

The resulting expanded random sequence is clearly nonstationary, because of the zero insertions.

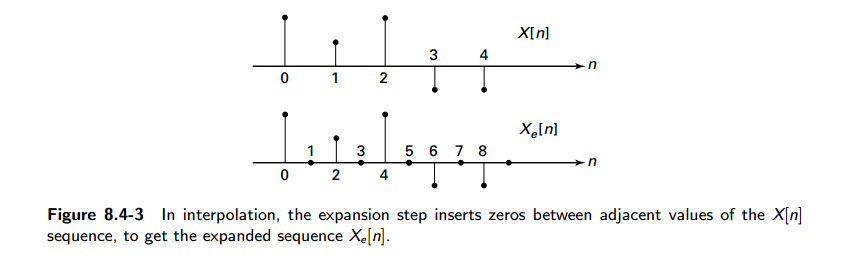
image-20250810194541608

This random sequences and processes is classified as being cyclostationary

psd of \(X_e[n]\), the expansion or the upsampled version of \(X[n]\)

\[ S_{X_eX_e}(\omega) = \frac{1}{L}S_{XX}(L\omega) \]

where \(L\) is upsampling factor

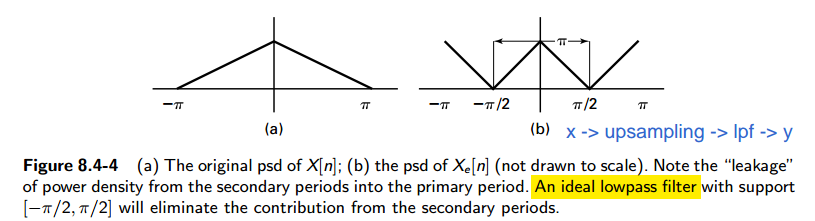
image-20250810204047368

apply \(X_e[n]\) to an ideal lowpass filter with bandwidth \([-\pi/2 , +\pi/2]\) and gain of \(2\) or \(L\)

\[ S_{YY}(\omega) = \left\{ \begin{array}{cl} L \cdot S_{XX}(L\omega), &\ |\omega|\leq \pi/L \\ 0, &\ \pi/L \lt |\omega| \leq \pi \end{array} \right. \]

Stark H, Woods JW. Probability, Statistics, and Random Processes for Engineers, 3rd [pdf]

—, 3th Ed Solution Manual [https://www.scribd.com/document/353335818/Stark-Woods-3th-Ed-Manual#page=212]

image-20250818222910938

General case with upsampling factor \(L\)

\[\begin{align} &\mathrm{E}\{|\sum_{n=-N}^N X_e[n]e^{-j\omega n}|^2\}\\ &= \sum_{n=-N}^N\sum_{l=-N}^NX_e[n]\cdot X_e^*[l]\cdot e^{-j\omega(n-l)}\\ &= \sum_{n=-N}^N\sum_{l=-N}^NX[\frac{n}{L}]\cdot X^*[\frac{l}{L}]\cdot e^{-j\omega(n-l)}\\ &= \sum_{k=-N/L}^{N/L}\sum_{m=-N/L}^{N/L}X[k]\cdot X^*[m]\cdot e^{-jL\omega (k-m)}\\ &= \sum_{k=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}R_{XX}[k-m]\cdot e^{-j\omega L(k-m)}\cdot \mathcal{rect}[\frac{k}{2N/L}]\cdot \mathcal{rect}[\frac{m}{2N/L}]\\ &= \sum_{i=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}R_{XX}[i]\cdot e^{-jL\omega i}\cdot \mathcal{rect}[\frac{i+m}{2N/L}]\cdot \mathcal{rect}[\frac{m}{2N/L}]\\ &= \sum_{i=-\infty}^{\infty}R_{XX}[i]\cdot e^{-jL\omega i} \cdot \frac{2N}{L}\left[1 -\frac{|i|}{2N/L} \right] \end{align}\]

Then \[\begin{align} S_{X_eX_e}(\omega) &= \lim_{N\to \infty}\frac{1}{2N+1}\cdot \mathrm{E}\{|\sum_{n=-N}^N X_e[n]e^{-j\omega n}|^2\} \\ &= \frac{1}{L}\sum_{i=-\infty}^{\infty}R_{XX}[i]\cdot e^{-jL\omega i}\\ &= \frac{1}{L}S_{XX}(L\omega) \end{align}\]

image-20250818211010290

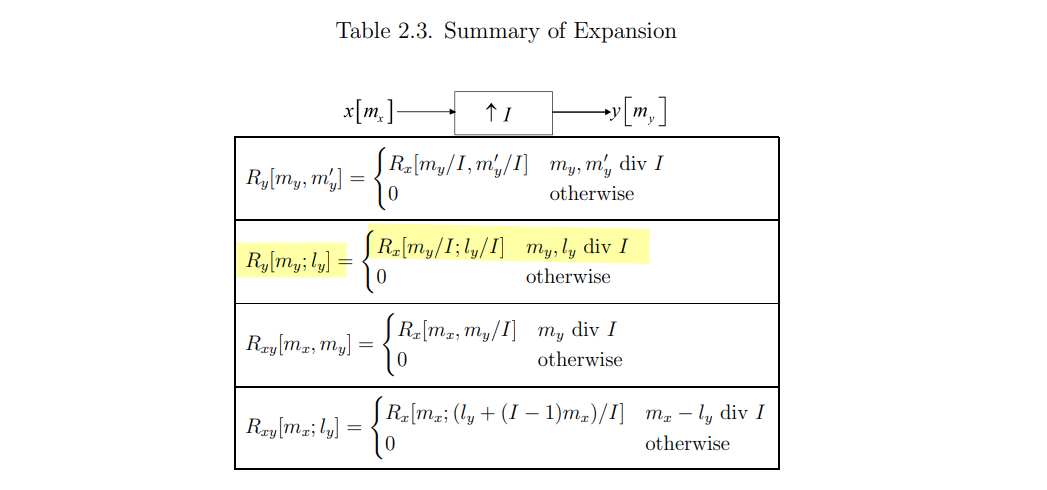
image-20250818205936474

Wiener Process (Brownian Motion)

Dennis Sun, Introduction to Probability: Lesson 49 Brownian Motion [https://dlsun.github.io/probability/brownian-motion.html]

Wiener process (also called Brownian motion)

unnamed-chunk-178-1

image-20241202001449997

NRZ PSD

image-20231111100420675

image-20231111101322771

image-20231110224237933

Lecture 26 Autocorrelation Functions of Random Binary Processes [https://bpb-us-e1.wpmucdn.com/sites.gatech.edu/dist/a/578/files/2003/12/ECE3075A-26.pdf]

Lecture 32 Correlation Functions & Power Density Spectrum, Cross-spectral Density [https://bpb-us-e1.wpmucdn.com/sites.gatech.edu/dist/a/578/files/2003/12/ECE3075A-32.pdf]

Normal Distribution and Input-Referred Noise [https://a2d2ic.wordpress.com/2013/06/05/normal-distribution-and-input-referred-noise/]

Fig.1 PDF for sum of a large number of random variables

Fig.2 The noise signal, its auto correlation function, and spectral density [2]

reference

L.W. Couch, Digital and Analog Communication Systems, 8th Edition, 2013 [pdf]

Alan V Oppenheim, George C. Verghese, Signals, Systems and Inference, 1st edition [pdf]

R. Ziemer and W. Tranter, Principles of Communications, Seventh Edition, 2013 [pdf]

Stark H, Woods JW. Probability, Statistics, and Random Processes for Engineers, 4th ed. 2012 [pdf]

Kuchler, Ryan J. Theory of multirate statistical signal processing and applications. Monterey, California.: Naval Postgraduate School, 2005. [pdf]

Balu Santhanam. Fall 2020 ECE541 Probability Theory & Stochastic Process [https://ece-research.unm.edu/bsanthan/ece541/]