Systems, Modulation and Noise

Posted on Edited on In

Modulation of WSS process

Balu Santhanam, Probability Theory & Stochastic Process 2020: Modulation of Random Processes

modulated with a random cosine

image-20241107202647998

Haykin, Simon S., and Michael Moher. Communication Systems. 5th ed. John Wiley & Sons, 2009. - Mixing of a Random Process with a Sinusoidal Process

image-20251116154457428

modulated with a deterministic cosine

image-20241107202947949

image-20241003001204803

Hayder Radha, ECE 458 Communications Systems Laboratory Spring 2008: Lecture 7 - EE 179: Introduction to Communications - Winter 2006–2007 Energy and Power Spectral Density and Autocorrelation

image-20241002231615792

image-20241002231639299

Quadrature-Modulated Processes

Haykin, Simon S., and Michael Moher. Communication Systems. 5th ed. John Wiley & Sons, 2009.

image-20251116160857679

Sampling of WSS process

Balu Santhanam, Probability Theory & Stochastic Process 2020: Impulse sampling of Random Processes

DT sequence \(x[n]\)

image-20240428162643394

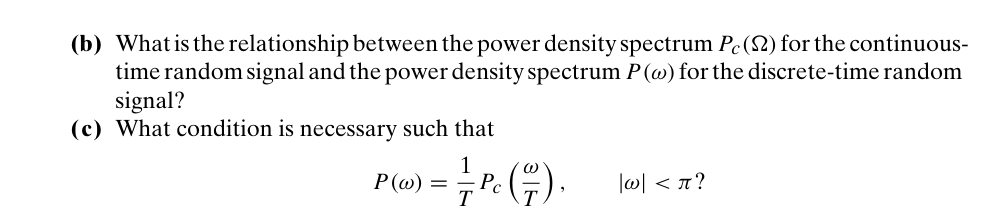
image-20240428162655969

image-20250812194041059

Owing to \(\phi[0] = \phi_c(0)\), the average power of the sampled version \(x[n]\) is the same as its input \(x_c(t)\)

impulse train \(x_s(t)\)

image-20241106222744962

image-20241106222817998

That is \[ P_{x_s x_s} (f)= \frac{1}{T_s^2}P_{xx}(f) \] where \(x[n]\) is sampled discrete-time sequence, \(x_s(t)\) is sampled impulse train

Noise Aliasing

apply foregoing observation

Pulsed Noise Signals

Chembian Thambidurai, "Power Spectral Density of Pulsed Noise Signals" [link]

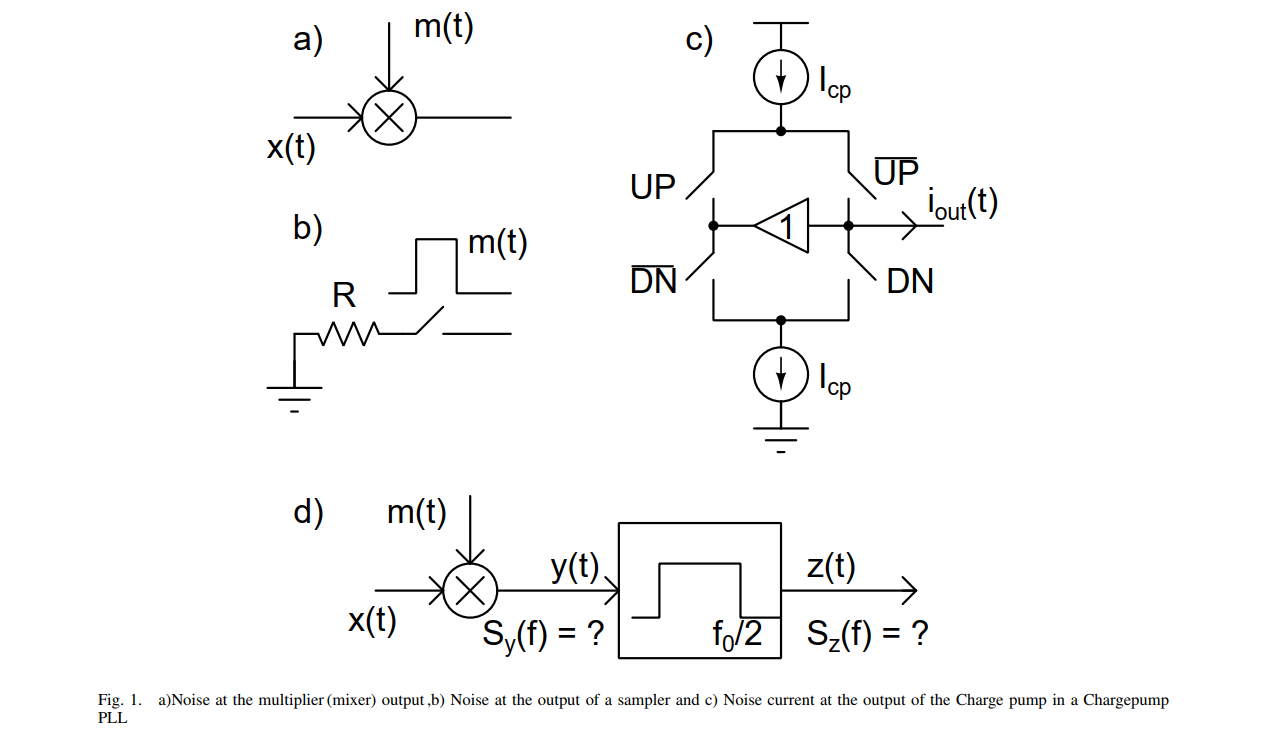
image-20241208075822212

Above, the output of the multiplier be \(y(t)\) is passed through a ideal brick wall low pass filter with a bandwidth of \(f_0/2\)

When a random signal is multiplied by a pulse function, the resulting signal becomes a cyclo-stationary random process.

As rule of thumb, the spectrum of such a pulsed noise signal

  • thermal noise is multiplied by \(\color{red}D\)

  • flicker noise is multiplied by \(\color{red}D^2\),

where \(D\) is the duty cycle of the pulse signal

image-20241208111744647

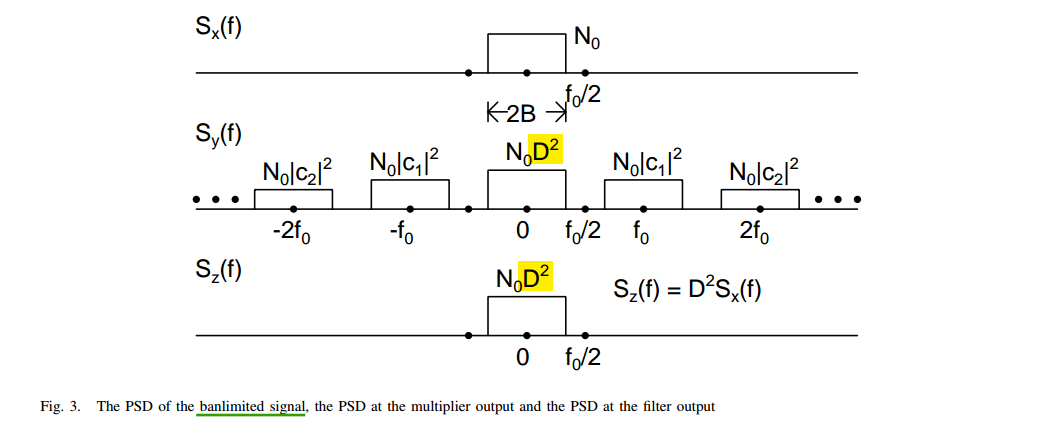
banlimited input (no aliasing)

image-20241208113904927

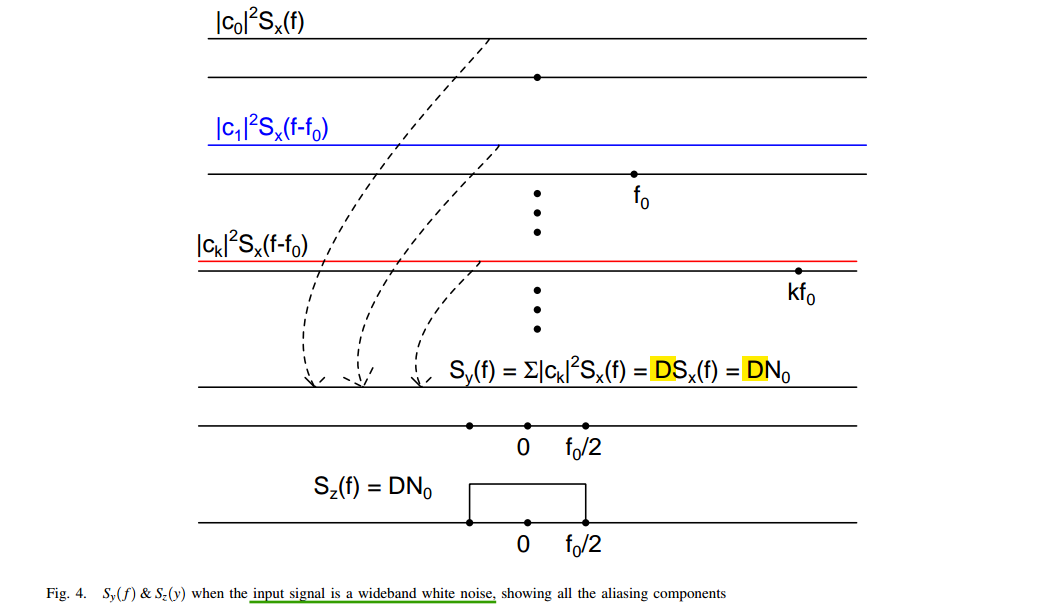
wideband white noise input

image-20241208114442705

flicker noise input

with \(S_x(f)=\frac{K_f}{f}\)

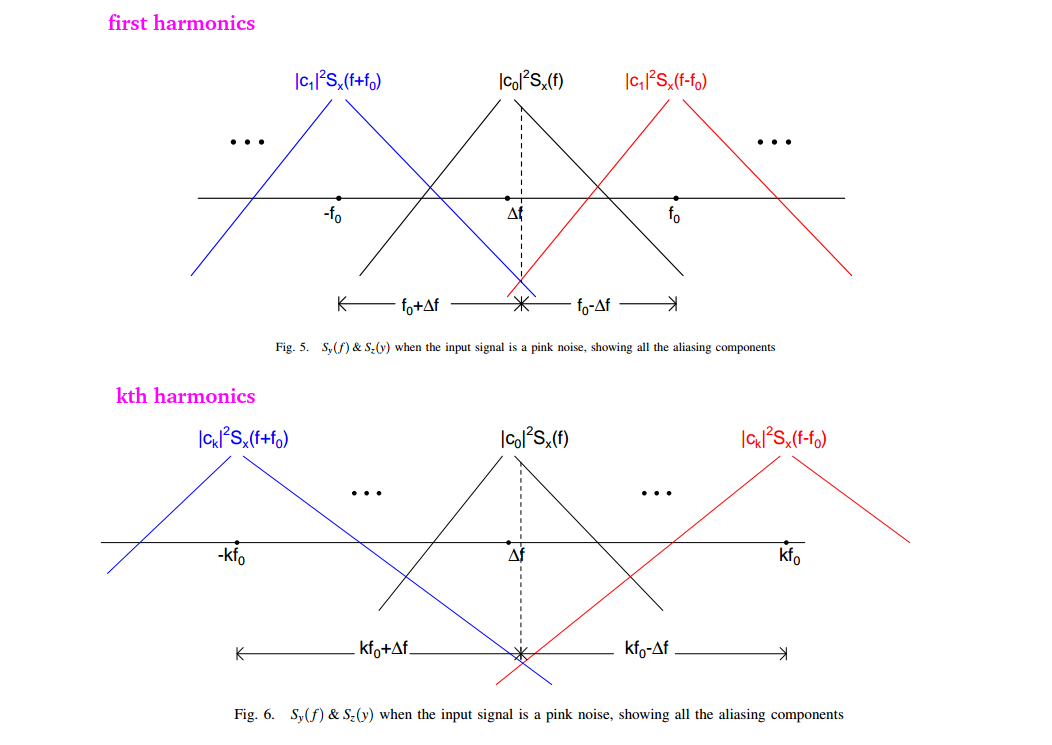
image-20241208121027250

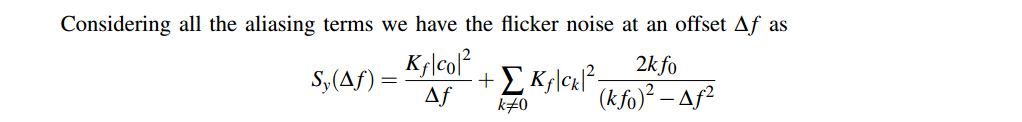
image-20241208121402724

Assuming \(\Delta f \ll f_0\)

image-20241208121645637

image-20241208111506517

Rectangular Pulse Sampling

Balu Santhanam. ece439 Introduction to Digital Signal Processing. Example: Rectangular Pulse Sampling [http://ece-research.unm.edu/bsanthan/ece439/recsamp.pdf]

image-20250810115325546

image-20250810115031537

reference

Alan V Oppenheim, Ronald W. Schafer. Discrete-Time Signal Processing, 3rd edition [pdf]

R. E. Ziemer and W. H. Tranter, Principles of Communications, 7th ed., Wiley, 2013 [pdf]

John G. Proakis and Masoud Salehi, Fundamentals of communication systems 2nd ed [pdf]

Rhee, W. and Yu, Z., 2024. Phase-Locked Loops: System Perspectives and Circuit Design Aspects. John Wiley & Sons

Lacaita, Andrea Leonardo, Salvatore Levantino, and Carlo Samori. Integrated frequency synthesizers for wireless systems. Cambridge University Press, 2007

Phillips, Joel R. and Kenneth S. Kundert. "Noise in mixers, oscillators, samplers, and logic: an introduction to cyclostationary noise." Proceedings of the IEEE 2000 Custom Integrated Circuits Conference. [pdf, slides]

Antoni, J., "Cyclostationarity by examples", Mechanical Systems and Signal Processing, vol. 23, no. 4, pp. 987–1036, 2009 [https://docente.unife.it/docenti/dleglc/a-a-2010-2011-dmsm/ciclostazionarieta.pdf]

Kundert, Ken. (2006). Simulating Switched-Capacitor Filters with SpectreRF. URL:https://designers-guide.org/analysis/sc-filters.pdf

STEADY-STATE AND CYCLO-STATIONARY RTS NOISE IN MOSFETS [https://ris.utwente.nl/ws/portalfiles/portal/6038220/thesis-Kolhatkar.pdf]

Christian-Charles Enz. "High precision CMOS micropower amplifiers" [pdf]

L.W. Couch, Digital and Analog Communication Systems, 8th Edition, Pearson, 2013.