Clocked Comparators
Noise Analysis
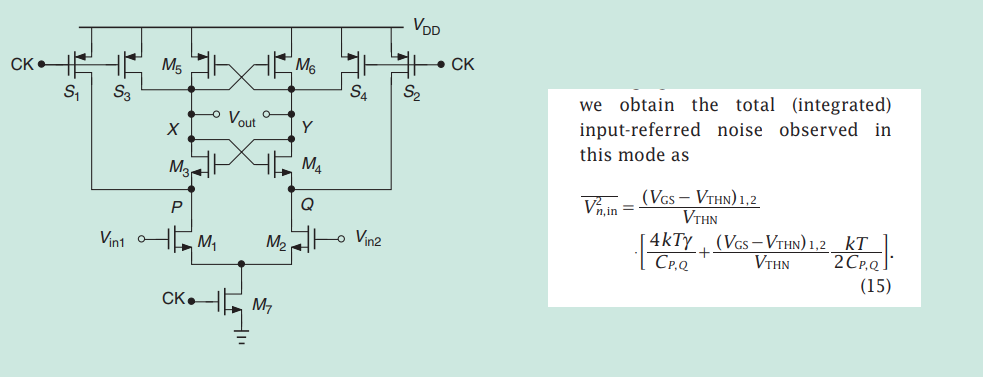
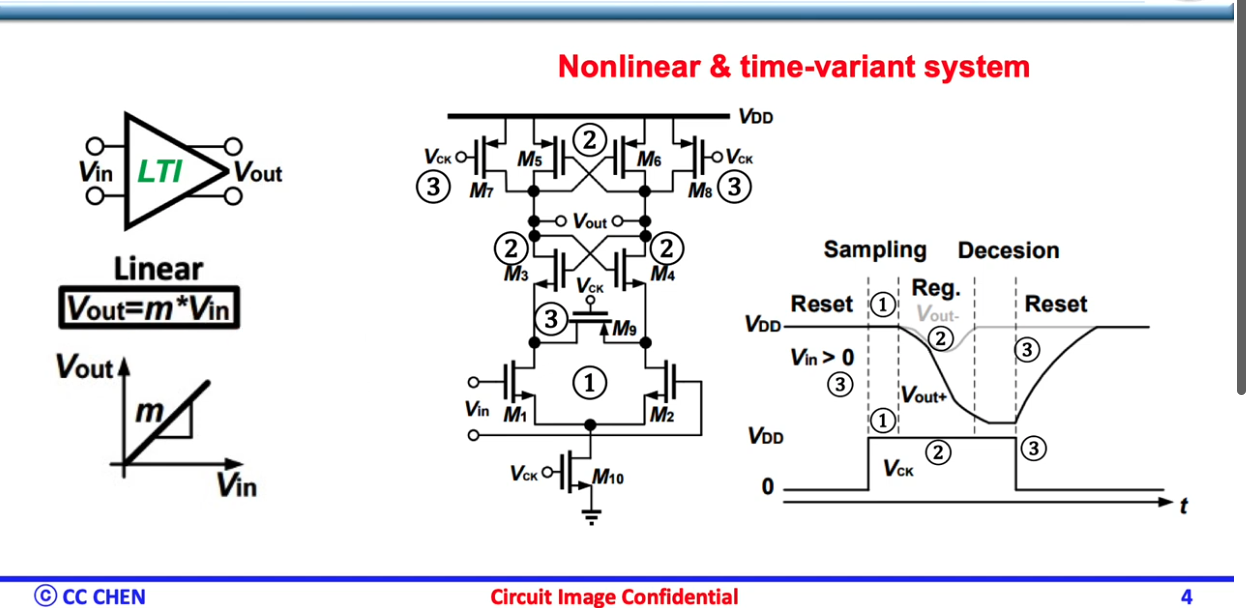
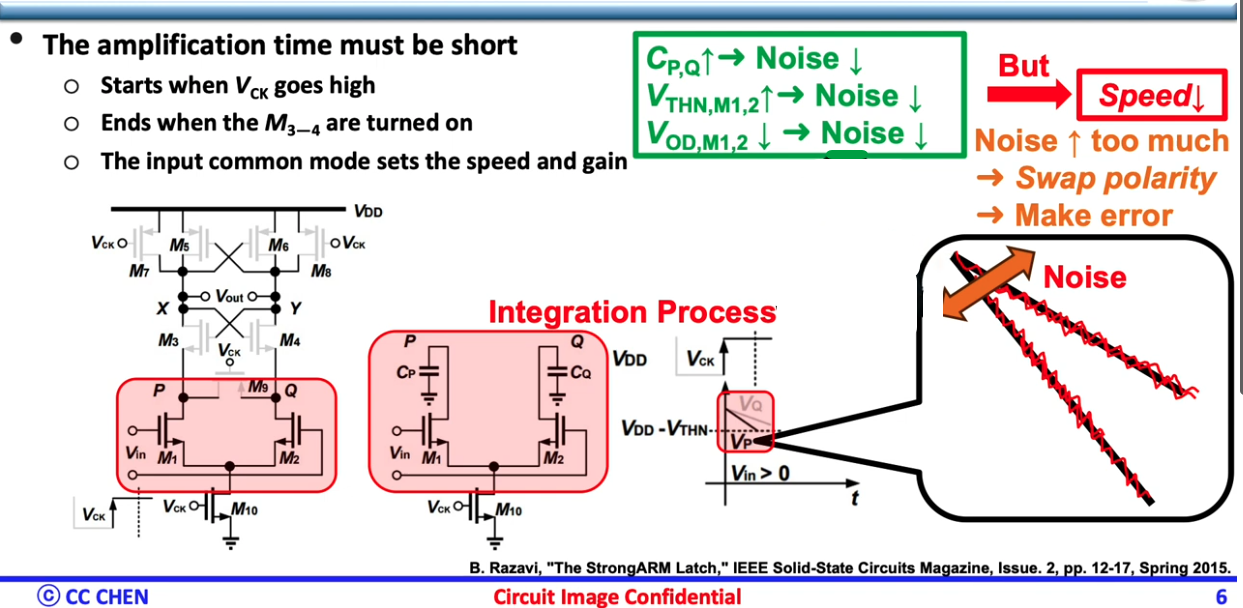
sampling (amplification) phase
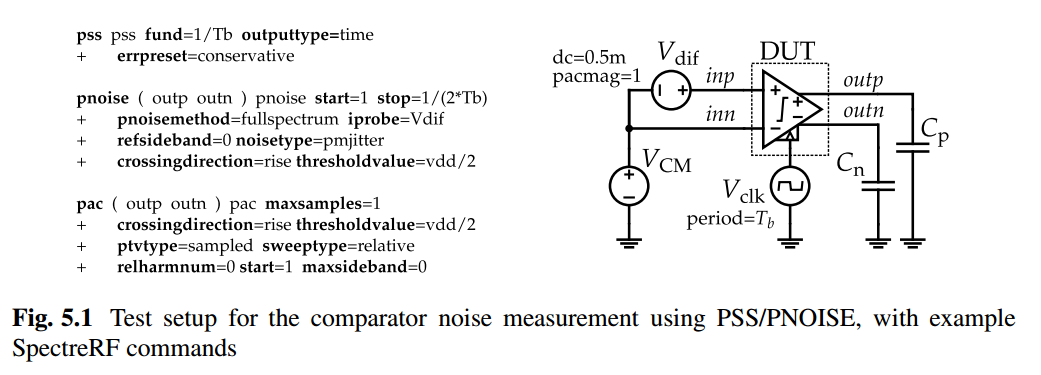
Noise Simulation
PSS + Pnoise Method
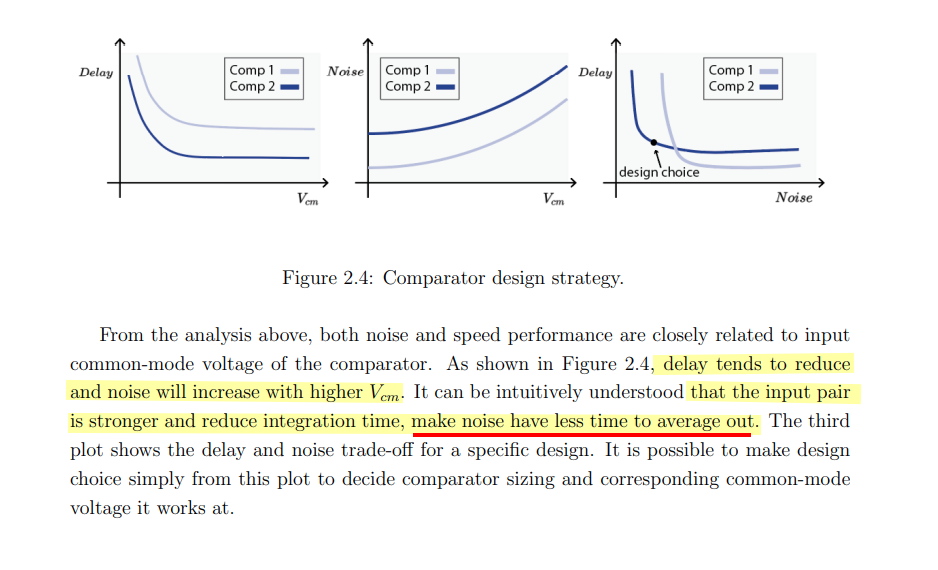
Comparator Output SNR during sampling region and decision region go up
Comparator Output SNR during regeneration region is constant, where noise is critical

Transient Noise Method
Noise Fmax sets the bandwidth of the random noise sources that are injected at each time point in the transient analysis
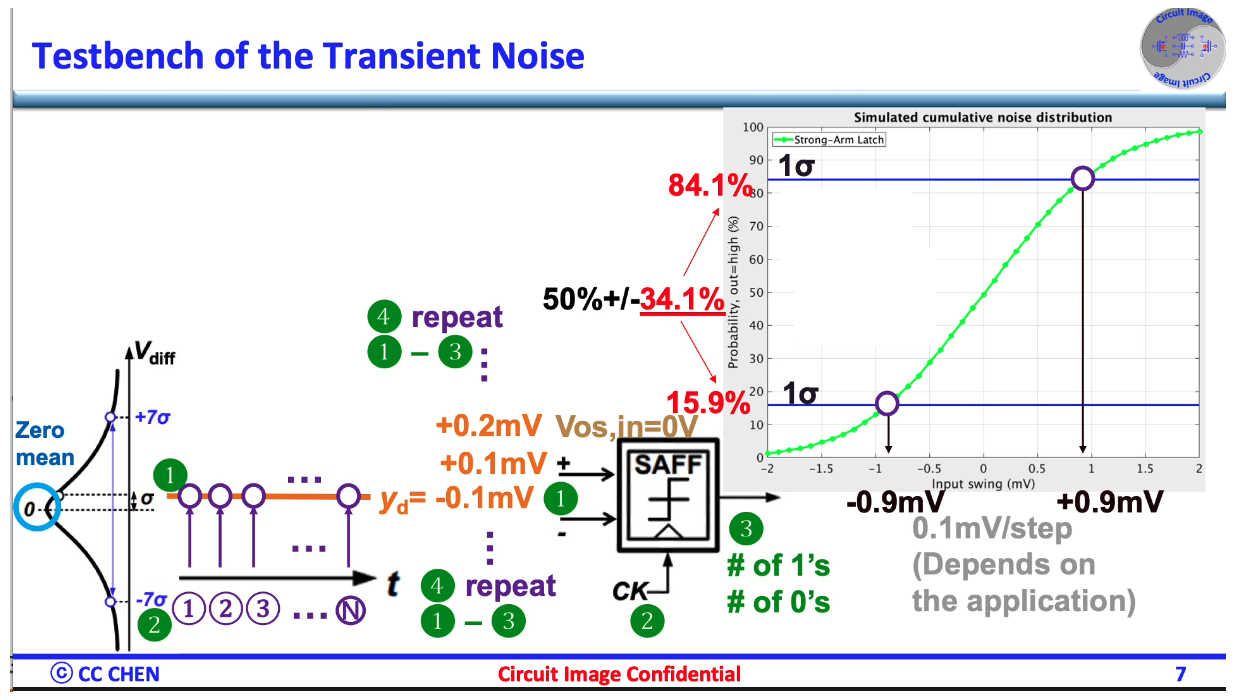
We can identify the RMS noise value easily by looking at 15.9% or 84.1% of CDF (\(1\sigma\)), the input-referred noise in the RMS is 0.9mV
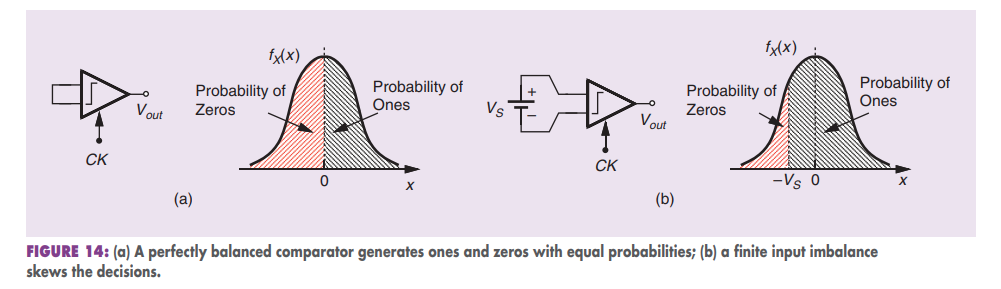
Thus, if \(V_S\) is chosen so as to reduce the probability of zeros to 16%, then \(V_S = 1\sigma\), which is also the total root-mean square (rms) noise referred to the input.
Comparison of two methods
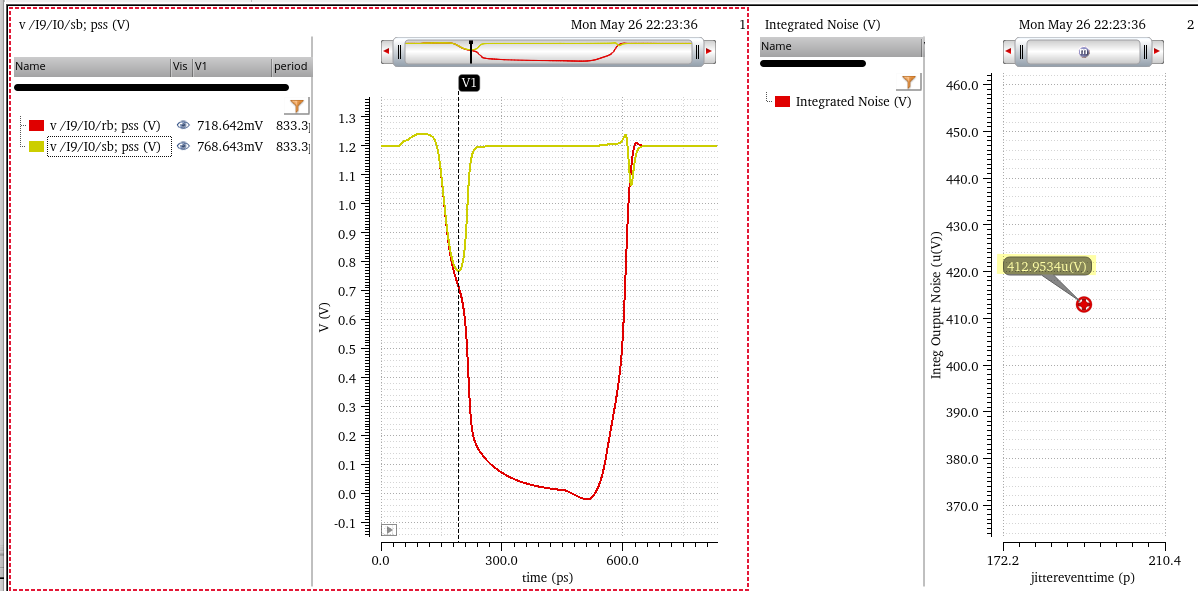
here, fundamental frequency = fclk; integrated noise (0 ~ 0.5fclk)
E. Gillen, G. Panchanan, B. Lawton and D. O'Hare, "Comparison of transient and PNOISE simulation techniques for the design of a dynamic comparator," 2022 33rd Irish Signals and Systems Conference (ISSC), Cork, Ireland, 2022, pp. 1-5
Chenguang Yang, "Comparator Design for High Speed ADC" [https://lup.lub.lu.se/luur/download?func=downloadFile&recordOId=9164380&fileOId=9164388]
J. Conrad, J. Kauffman, S. Wilhelmstatter, R. Asthana, V. Belagiannis and M. Ortmanns, "Confidence Estimation and Boosting for Dynamic-Comparator Transient-Noise Analysis," 2024 22nd IEEE Interregional NEWCAS Conference (NEWCAS), Sherbrooke, QC, Canada, 2024, pp. 1-5
There are some ambiguity in formula in ADC Verification Rapid Adoption Kit (RAK)(Product Version: IC 6.1.8, SPECTRE 18.1 March, 2019)
- Transient Noise Analysis: \(\sqrt{2}\sigma\), why ratio \(\sqrt{2}\) ???
- PSS+Pnoise: why two fundamental tones fclk/2 ???
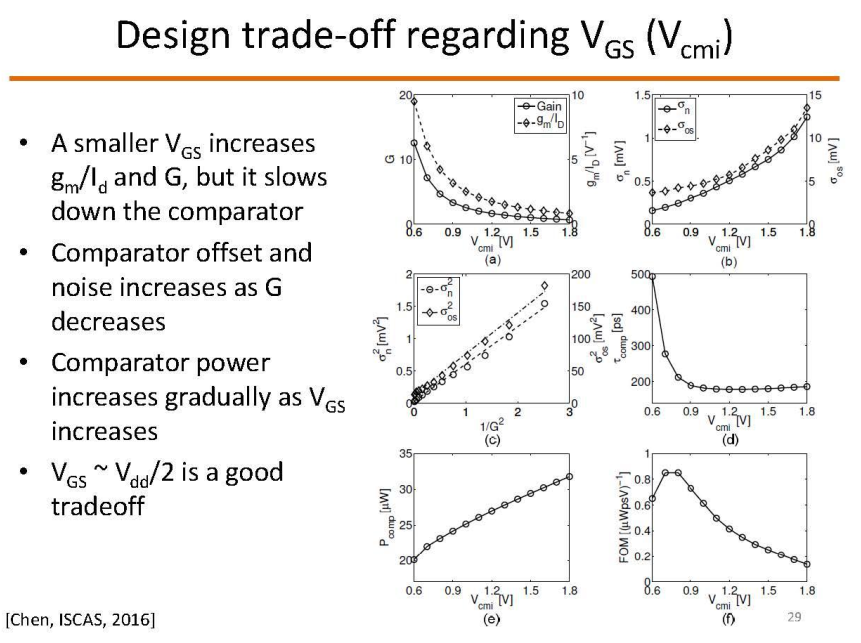
Common-Mode (Vcmi) Variation Effects

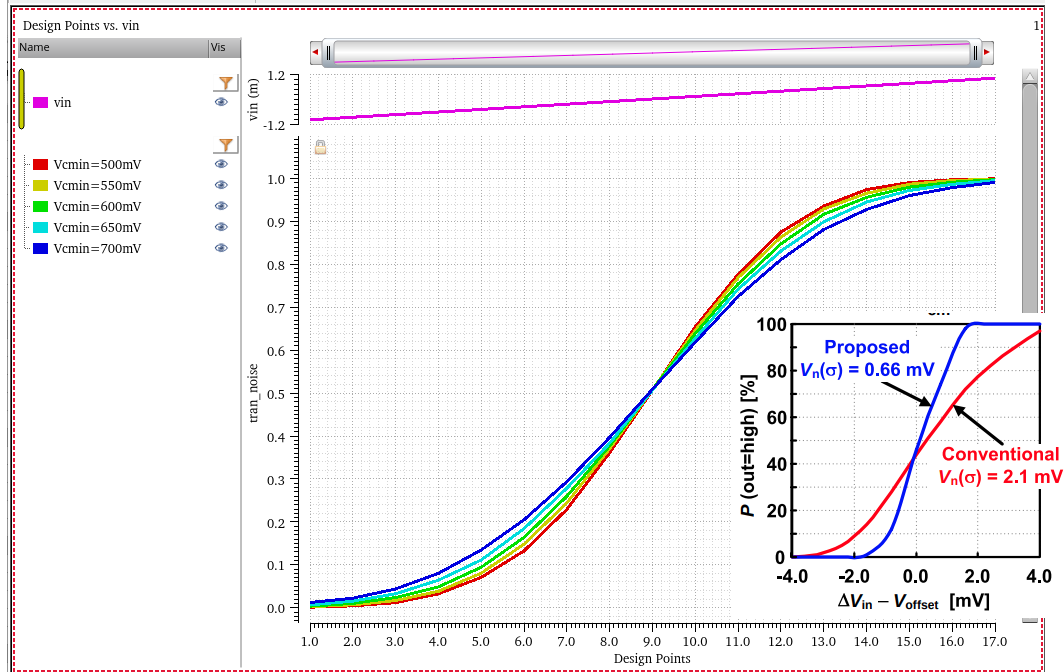
Zhaokai Liu. Time-interleaved SAR ADC Design Using Berkeley Analog Generator [https://www2.eecs.berkeley.edu/Pubs/TechRpts/2020/EECS-2020-109.pdf]
offset simulation
T. Caldwell. ECE 1371S Advanced Analog Circuits [http://individual.utoronto.ca/trevorcaldwell/course/comparators.pdf]
Eric Chang. EECS240-s18 Discussion 9
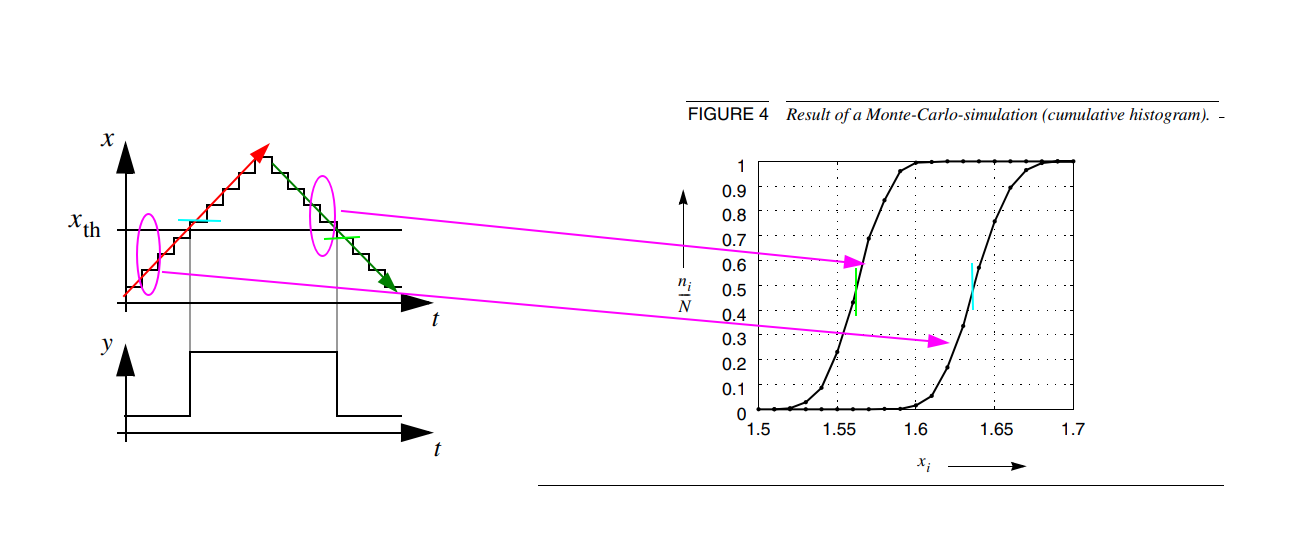
Graupner, Achim & Sobe, Udo. (2007). Offset-Simulation of Comparators. [https://designers-guide.org/analysis/comparator.pdf]
2
3
4
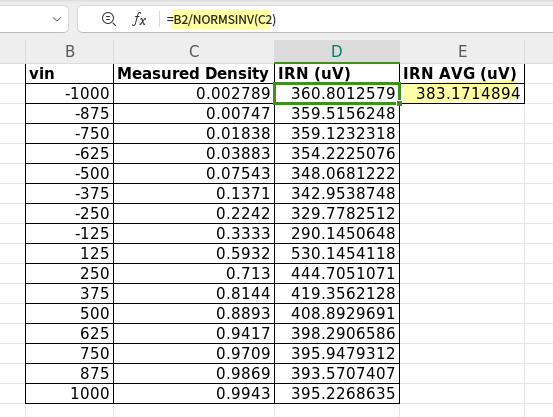
If the input referred offset follows a normal distribution than it is sufficient to apply a single offset voltage to calculate the offset voltage.
See details in Razavi, B., The StrongARM Latch [A Circuit for All Seasons], IEEE Solid-State Circuits Magazine, Volume:7, Issue: 2, Spring 2015
Omran, Hesham. (2019). Fast and accurate technique for comparator offset voltage simulation. Microelectronics Journal. 89. 10.1016/j.mejo.2019.05.004.
Matthews, Thomas W. and Perry L. Heedley. “A simulation method for accurately determining DC and dynamic offsets in comparators.” 48th Midwest Symposium on Circuits and Systems, 2005. (2005): 1815-1818 Vol. 2. [https://athena.ecs.csus.edu/~pheedley/MSDL/MSDL_DOTB_cmp_test_bench_MWSCAS05.pdf]
Hysteresis
P. Bruschi: Notes on Mixed Signal Design http://www2.ing.unipi.it/~a008309/mat_stud/MIXED/archive/2019/Optional_notes/Chap_3_4_Comparators.pdf
TODO 📅
Kickback Noise
Kickback noise trades with the dimensions of the input transistors and hence with the offset voltage
- affects the comparator's own decision
- corrupts the input voltage while it is sensed by other circuits

Tetsuya Iizuka,VLSI2021_Workshop3 "Nyquist A/D Converter Design in Four Days"
Figueiredo, Pedro & Vital, João. (2006). Kickback noise reduction techniques for CMOS latched comparators. Circuits and Systems II: Express Briefs, IEEE Transactions on. 53. 541 - 545. 10.1109/TCSII.2006.875308. [https://sci-hub.se/10.1109/TCSII.2006.875308]
P. M. Figueiredo and J. C. Vital, "Low kickback noise techniques for CMOS latched comparators," 2004 IEEE International Symposium on Circuits and Systems (ISCAS), Vancouver, BC, Canada, 2004, pp. I-537 [https://sci-hub.se/10.1109/ISCAS.2004.1328250]
Lei, Ka Meng & Mak, Pui-In & Martins, R.P.. (2013). Systematic analysis and cancellation of kickback noise in a dynamic latched comparator. Analog Integrated Circuits and Signal Processing. 77. 277-284. 10.1007/s10470-013-0156-1. [https://rto.um.edu.mo/wp-content/uploads/docs/ruimartins_cv/publications/journalpapers/57.pdf]
O. M. Ívarsson, "Comparator Kickback Reduction Techniques for High-Speed ADCs," Dissertation, 2024. [https://liu.diva-portal.org/smash/get/diva2:1872476/FULLTEXT01.pdf]
Current mirrors are used between stages to reduce charge kick back from the logic level swing of the latch onto the small comparator input capacitors
Mike Shuo-Wei Chen and R. W. Brodersen, "A 6-bit 600-MS/s 5.3-mW Asynchronous ADC in 0.13-μm CMOS," in IEEE Journal of Solid-State Circuits, vol. 41, no. 12, pp. 2669-2680, Dec. 2006 [pdf, slides]
K. Bult and A. Buchwald, "An embedded 240-mW 10-b 50-MS/s CMOS ADC in 1-mm/sup 2/," in IEEE Journal of Solid-State Circuits, vol. 32, no. 12, pp. 1887-1895, Dec. 1997 [https://sci-hub.st/10.1109/4.643647]
CMOS Latch
TODO 📅
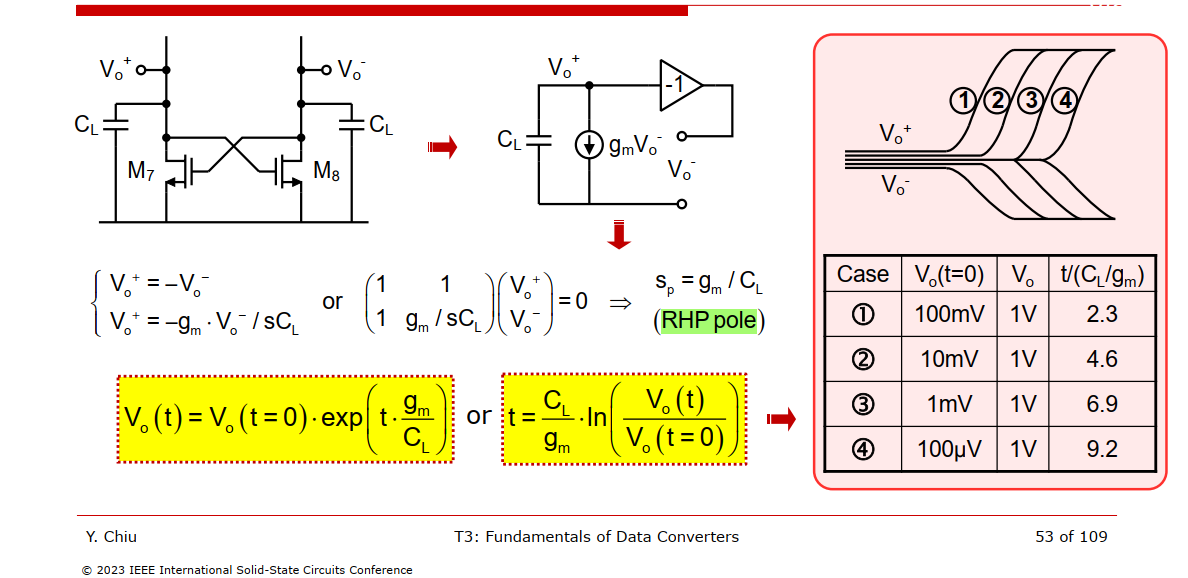 \[
V_{o,fb}^+ - V_{o,fb}^- = \frac{g_m}{sC_L}(V_o^+ - V_o^-) =
A(s)\cdot(V_o^+ - V_o^-)
\]
\[
V_{o,fb}^+ - V_{o,fb}^- = \frac{g_m}{sC_L}(V_o^+ - V_o^-) =
A(s)\cdot(V_o^+ - V_o^-)
\]
We have \[ A(s)\cdot (V_{i} + V_o) = V_o \]
that is \[ V_o = \frac{A(s)}{1-A(s)}V_{i} = \frac{1}{s - g_m/C_L}\cdot \frac{g_mV_i}{C_L} \]
therefore \[
V_o(t) = \frac{g_mV_i}{C_L}\cdot\exp\left({\frac{g_m}{C_L}t}\right) =
V_o(t=0)\cdot\exp\left({\frac{g_m}{C_L}t}\right)
\] 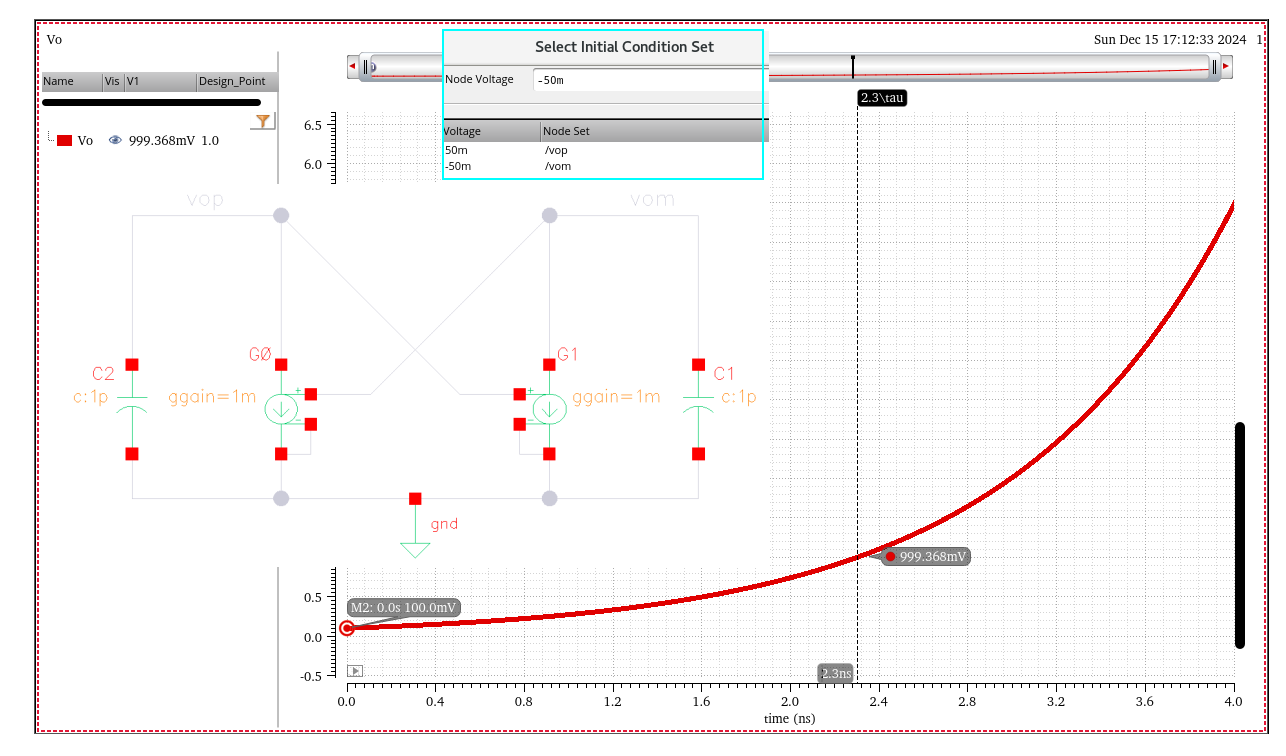
Asad Abidi, ISSCC 2023: Circuit Insights "The CMOS Latch" [https://youtu.be/sVe3VUTNb4Q?si=Pl75jWiA0kNPOlOs]
Metastability
TODO 📅
If the comparator can not generate a well-defined logical output in half of the clock period, we say the circuit is "metastable"
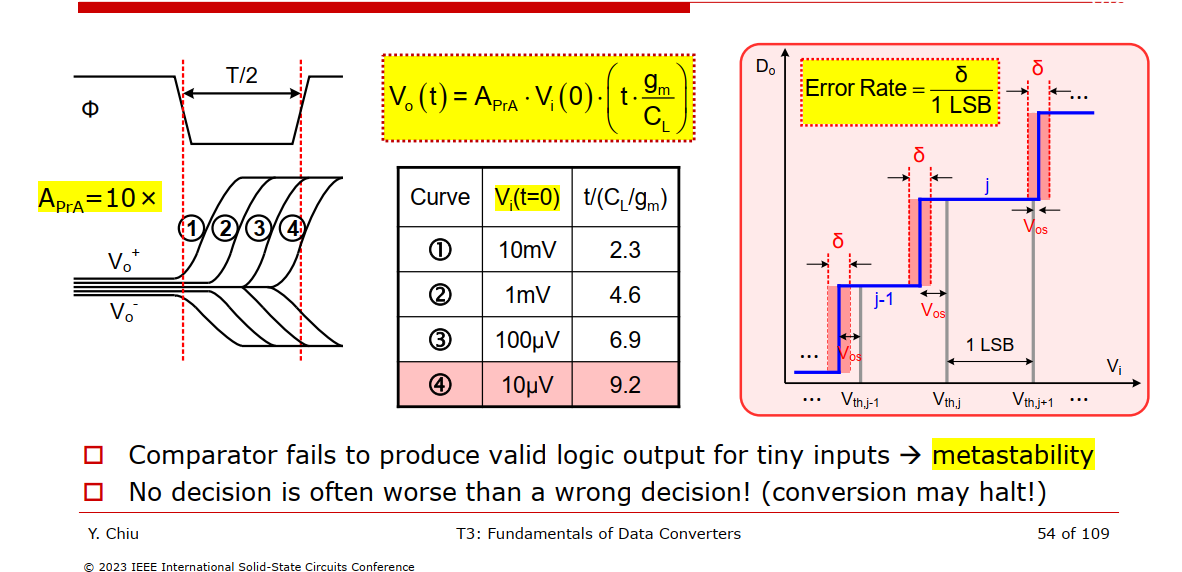
Math Background
Relating \(\Phi\) and erf
Error Function (Erf) of the standard Normal distribution \[ \text{Erf}(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2} \mathrm{d}t. \] Cumulative Distribution Function (CDF) of the standard Normal distribution \[ \Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^x e^{-z^2/2} \mathrm{d}z. \]
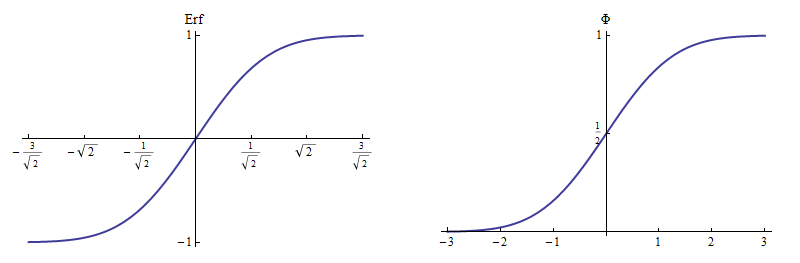
\[\begin{align} \Phi(x) &= \frac{\text{Erf}(x/\sqrt{2})+1}{2}. \\ \Phi(x\sqrt{2}) &= \frac{\text{Erf}(x) + 1}{2} \end{align}\]
Considering the mean and standard deviation \[ \Phi(x,\mu,\sigma)=\frac{1}{2}\left( 1+\text{Erf} \left( \frac{x-\mu}{\sigma\sqrt{2}} \right)\right) \]

John D. Cook. Relating Φ and erf [https://www.johndcook.com/erf_and_normal_cdf.pdf]
reference
Xu, H. (2018). Mixed-Signal Circuit Design Driven by Analysis: ADCs, Comparators, and PLLs. UCLA. ProQuest ID: Xu_ucla_0031D_17380. Merritt ID: ark:/13030/m5f52m8x. Retrieved from [https://escholarship.org/uc/item/88h8b5t3]
A. Abidi and H. Xu, "Understanding the Regenerative Comparator Circuit," Proceedings of the IEEE 2014 Custom Integrated Circuits Conference, San Jose, CA, 2014, pp. 1-8. [https://picture.iczhiku.com/resource/ieee/WHiYwoUjPHwZPXmv.pdf]
T. Sepke, P. Holloway, C. G. Sodini and H. -S. Lee, "Noise Analysis for Comparator-Based Circuits," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 56, no. 3, pp. 541-553, March 2009 [https://dspace.mit.edu/bitstream/handle/1721.1/61660/Speke-2009-Noise%20Analysis%20for%20Comparator-Based%20Circuits.pdf]
Sepke, Todd. "Comparator design and analysis for comparator-based switched-capacitor circuits." (2006). [https://dspace.mit.edu/handle/1721.1/38925]
P. Nuzzo, F. De Bernardinis, P. Terreni and G. Van der Plas, "Noise Analysis of Regenerative Comparators for Reconfigurable ADC Architectures," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 55, no. 6, pp. 1441-1454, July 2008 [https://picture.iczhiku.com/resource/eetop/SYirpPPPaAQzsNXn.pdf]
J. Kim, B. S. Leibowitz, J. Ren and C. J. Madden, "Simulation and Analysis of Random Decision Errors in Clocked Comparators," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 56, no. 8, pp. 1844-1857, Aug. 2009, doi: 10.1109/TCSI.2009.2028449. URL:https://people.engr.tamu.edu/spalermo/ecen689/simulation_analysis_clocked_comparators_kim_tcas1_2009.pdf
J. Kim, B. S. Leibowitz and M. Jeeradit, "Impulse sensitivity function analysis of periodic circuits," 2008 IEEE/ACM International Conference on Computer-Aided Design, 2008, pp. 386-391, doi: 10.1109/ICCAD.2008.4681602. [https://websrv.cecs.uci.edu/~papers/iccad08/PDFs/Papers/05C.2.pdf]
Jaeha Kim, Lecture 12. Aperture and Noise Analysis of Clocked Comparators URL:https://ocw.snu.ac.kr/sites/default/files/NOTE/7038.pdf
Sam Palermo. ECEN720: High-Speed Links Circuits and Systems Spring 2023 Lecture 6: RX Circuits [https://people.engr.tamu.edu/spalermo/ecen689/lecture6_ee720_rx_circuits.pdf]
Y. Luo, A. Jain, J. Wagner and M. Ortmanns, "Input Referred Comparator Noise in SAR ADCs," in IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 66, no. 5, pp. 718-722, May 2019. [https://sci-hub.se/10.1109/TCSII.2019.2909429]
X. Tang et al., "An Energy-Efficient Comparator With Dynamic Floating Inverter Amplifier," in IEEE Journal of Solid-State Circuits, vol. 55, no. 4, pp. 1011-1022, April 2020 [https://sci-hub.se/10.1109/JSSC.2019.2960485]
Chen, Long & Sanyal, Arindam & Ma, Ji & Xiyuan, Tang & Sun, Nan. (2016). Comparator Common-Mode Variation Effects Analysis and its Application in SAR ADCs. 10.1109/ISCAS.2016.7538972. [https://labs.engineering.asu.edu/mixedsignals/wp-content/uploads/sites/58/2017/08/ISCAS_comp_long_2016.pdf]
V. Stojanovic, and V. G. Oklobdzija, "Comparative Analysis of Master–Slave Latches and Flip-Flops for High-Performance and Low-Power Systems," IEEE J. Solid-State Circuits, vol. 34, pp. 536–548, April 1999. [https://www.ece.ucdavis.edu/~vojin/CLASSES/EEC280/Web-page/papers/Clocking/Vlada-Latches-JoSSC-Apr-1999.pdf]
C. Mangelsdorf, "Metastability: Deeply misunderstood [Shop Talk: What You Didn’t Learn in School]," in IEEE Solid-State Circuits Magazine, vol. 16, no. 2, pp. 8-15, Spring 2024
Rabuske, Taimur & Fernandes, Jorge. (2014). Noise-aware simulation-based sizing and optimization of clocked comparators. Analog Integr. Circuits Signal Process.. 81. 723-728. 10.1007/s10470-014-0428-4. [https://sci-hub.se/10.1007/s10470-014-0428-4]
Rabuske, Taimur & Fernandes, Jorge. (2016). Charge-Sharing SAR ADCs for Low-Voltage Low-Power Applications. 10.1007/978-3-319-39624-8.
Masaya Miyahara, Yusuke Asada, Daehwa Paik and Akira Matsuzawa, "A low-noise self-calibrating dynamic comparator for high-speed ADCs," 2008 IEEE Asian Solid-State Circuits Conference, Fukuoka, Japan, 2008 [slides, paper]
Art Schaldenbrand, Senior Product Manager, Keeping Things Quiet: A New Methodology for Dynamic Comparator Noise Analysis URL:https://www.cadence.com/content/dam/cadence-www/global/en_US/videos/tools/custom-_ic_analog_rf_design/NoiseAnalyisposting201612Chalk%20Talk.pdf
B. Razavi, "The Design of a Comparator [The Analog Mind]," IEEE Solid-State Circuits Magazine, Volume. 12, Issue. 4, pp. 8-14, Fall 2020. [https://www.seas.ucla.edu/brweb/papers/Journals/BR_SSCM_4_2020.pdf]
—, "The StrongARM Latch [A Circuit for All Seasons]," IEEE Solid-State Circuits Magazine, Issue. 2, pp. 12-17, Spring 2015. [https://www.seas.ucla.edu/brweb/papers/Journals/BR_Magzine4.pdf]
B. Murmann. ISSCC 2011 Tutorial: Noise Analysis in Switched Capacitor Circuits [slides, transcription]
—, "Thermal Noise in Track-and-Hold Circuits: Analysis and Simulation Techniques," IEEE Solid-State Circuits Magazine, vol. 4, no. 2, pp. 46-54, June 2012 [https://sci-hub.se/10.1109/MSSC.2012.2192190]
X. Huang. Thermal noise analysis of switched-capacitor amplifier [theory, simulation]
CHUNG-CHUN (CC) CHEN. Why A Dedicated Noise Analysis for A Strong-arm Latch / Comparator? [https://youtu.be/S5GnvFxuxUA]
—. Why Transient Noise (Trannoise) Analysis for A Strong-arm Latch / Comparator? [https://youtu.be/gpQggSM9_PE]
—. Why A Periodic Steady-State (PSS), Periodic Noise (Pnoise), and Hand Calculation for A Sampler? [https://youtu.be/lGqCfg5R-rY]
Tony Chan Carusone,. 28 Comparator Specs and Characterization [https://youtu.be/mRfWM1bpr3k]
Prof. Seung-Tak Ryu (KAIST) "Advanced ADC Design Techniques" Online Course (2022) : Dynamic Latch [https://youtu.be/zE1ZdG_XzWk]
IC宇宙成长记. 动态比较器噪声仿真 [link]