Equalization & Timing Recovery
Multipliers
TODO 📅
Adders
TODO 📅
overlapped tuning range
TODO 📅
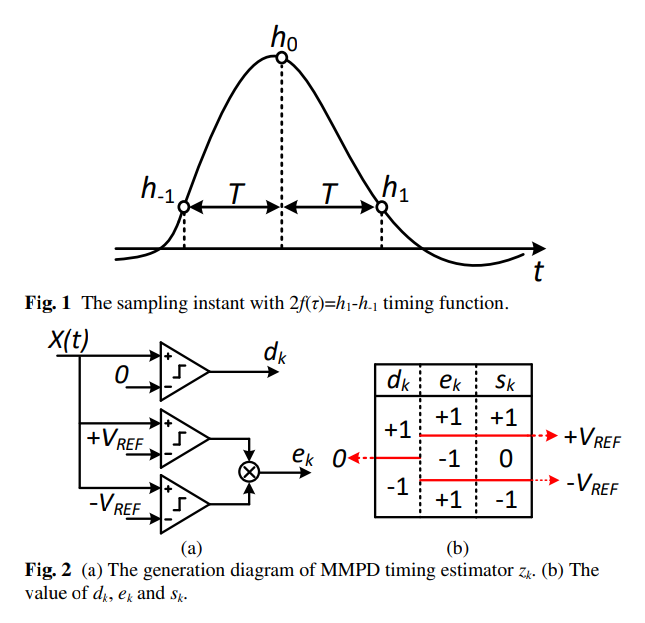
Mueller-Muller PD
Mueller-Muller type A timing function

Mueller-Muller type B timing function

Least-Mean-Square (LMS)
minimum mean square error (MMSE)
This simplified version of LMS algorithm is identical to the zero-forcing algorithm which minimizes the ISI at data samples
Sign-Sign LMS (SS-LMS)
T11: Basics of Equalization Techniques: Channels, Equalization, and Circuits, 2022 IEEE International Solid-State Circuits Conference
V. Stojanovic et al., "Autonomous dual-mode (PAM2/4) serial link transceiver with adaptive equalization and data recovery," in IEEE Journal of Solid-State Circuits, vol. 40, no. 4, pp. 1012-1026, April 2005, doi: 10.1109/JSSC.2004.842863.
Jinhyung Lee, Design of High-Speed Receiver for Video Interface with Adaptive Equalization; Phd thesis, August 2019. thesis link
Paulo S. R. Diniz, Adaptive Filtering: Algorithms and Practical Implementation, 5th edition
E. -H. Chen et al., "Near-Optimal Equalizer and Timing Adaptation for I/O Links Using a BER-Based Metric," in IEEE Journal of Solid-State Circuits, vol. 43, no. 9, pp. 2144-2156, Sept. 2008
DFE h0 Estimator
summer output \[ r_k = a_kh_0+\left(\sum_{n=-\infty,n\neq0}^{+\infty}a_{k-n}h_n-\sum_{n=1}^{\text{ntap}}\hat{a}_{k-n}\hat{h}_n\right) \] error slicer analog output \[ e_k=r_k-\hat{a}_k \hat{h}_0 \] error slicer digital output \[ \hat{e}_k=|e_k| \] It's NOT possible to implement \(e_k\), which need to determine \(\hat{a}_k=|r_k|\) in no time. One method to approach this problem is calculate \(e_k^{a_k=1}=r_k-\hat{a}_k \hat{h}_0\) and \(e_k^{a_k=-1}=r_k+\hat{a}_k \hat{h}_0\), then select the right one based on \(\hat{a}_k\)
The update equation based on Sign-Sign-Least Mean square (SS-LMS) and loss function \(L(\hat{h}_{\text{0~ntap}})=E(e_k^2)\) \[ \hat{h}_n(k+1) = \hat{h}_n(k)+\mu \cdot |e_k|\cdot \hat{a}_{k-n} \] Where \(n \in [0,...,\text{ntap}]\). This way, we can obtain \(\hat{h}_0\), \(\hat{h}_1\), \(\hat{h}_2\), ...
\(\hat{h}_0\) is used in AFE adaptation
We may encounter difficulty if the first tap of DFE is unrolled, its \(e_k\) is modified as follow \[ r_k = a_kh_0+\left(\sum_{n=-\infty,n\neq0}^{+\infty}a_{k-n}h_n-\sum_{n=2}^{\text{ntap}}\hat{a}_{k-n}\hat{h}_n\right) \] Where there is NO \(\hat{h}_1\)
To find \(\hat{h}_1\), we shall use different pattern for even and odd error slicer
Maximum Likelihood Sequence Estimator (MLSE)
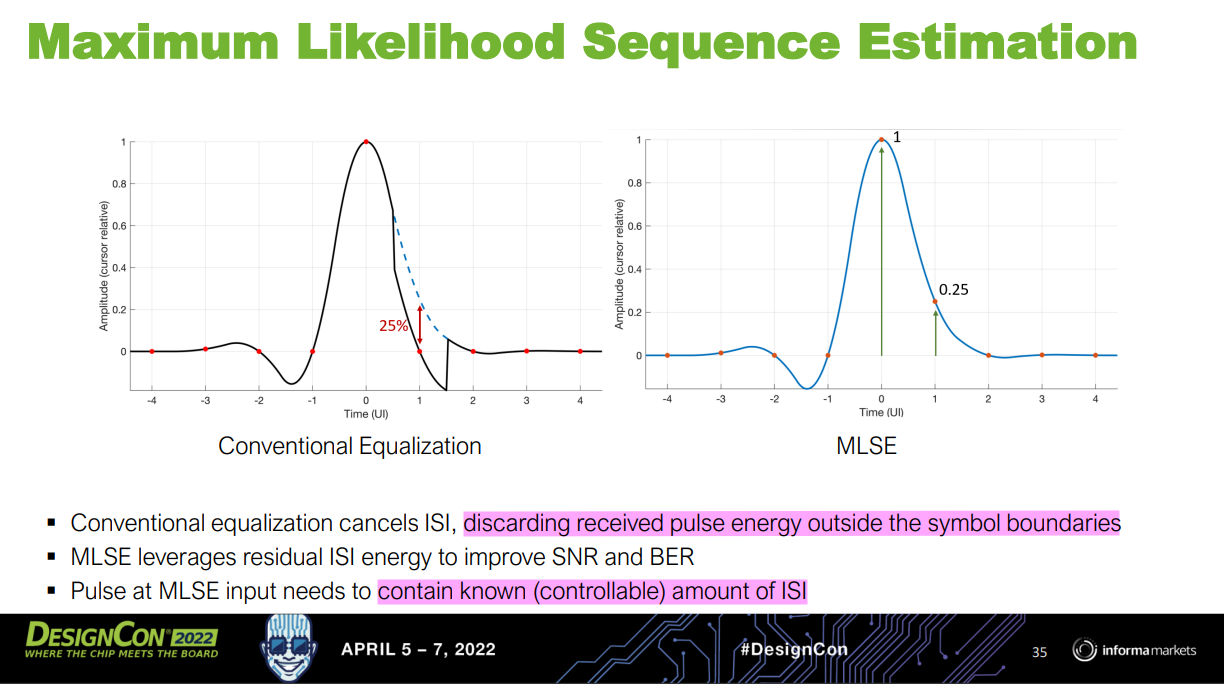
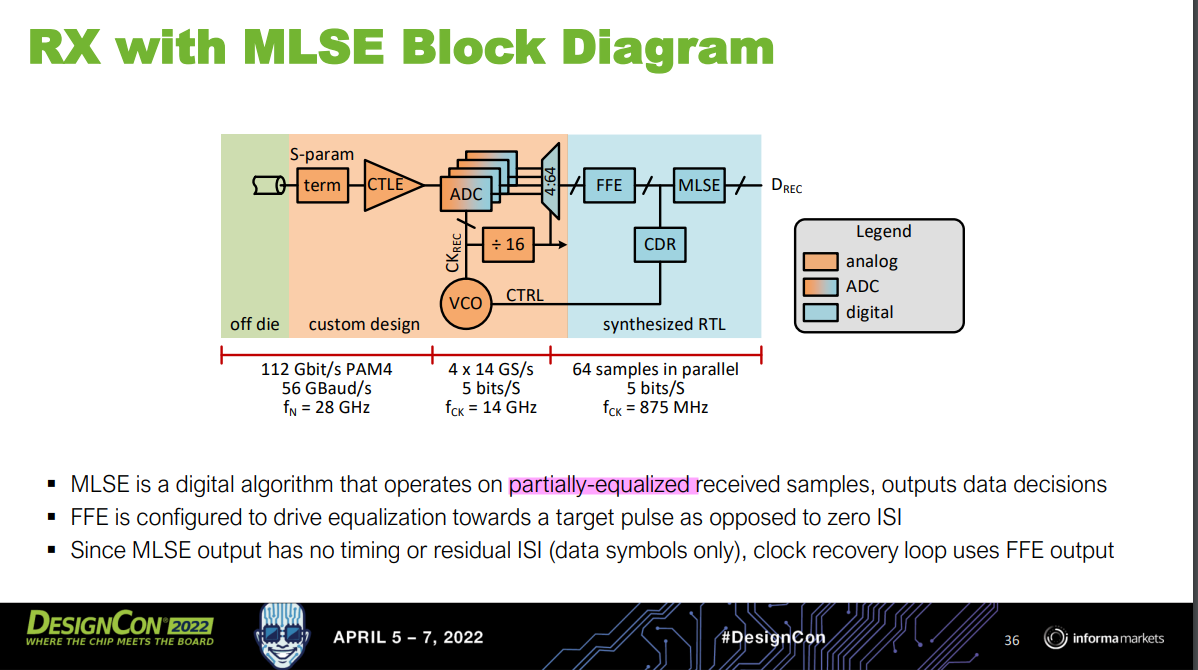
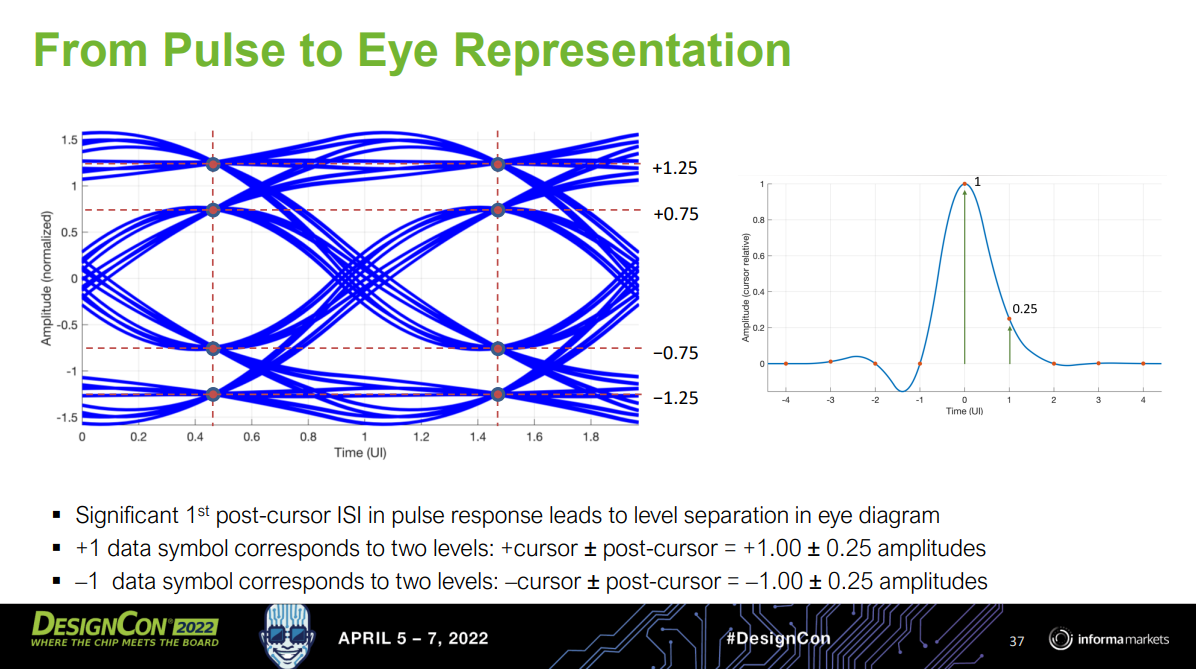
[IBIS-AMI Modeling and Correlation Methodology for ADC-Based SerDes Beyond 100 Gb/s https://static1.squarespace.com/static/5fb343ad64be791dab79a44f/t/63d807441bcd266de258b975/1675102025481/SLIDES_Track02_IBIS_AMI_Modeling_and_Correlation_Tyshchenko.pdf]
M. Emami Meybodi, H. Gomez, Y. -C. Lu, H. Shakiba and A. Sheikholeslami, "Design and Implementation of an On-Demand Maximum-Likelihood Sequence Estimation (MLSE)," in IEEE Open Journal of Circuits and Systems, vol. 3, pp. 97-108, 2022, doi: 10.1109/OJCAS.2022.3173686.
Zaman, Arshad Kamruz (2019). A Maximum Likelihood Sequence Equalizing Architecture Using Viterbi Algorithm for ADC-Based Serial Link. Undergraduate Research Scholars Program. Available electronically from [https://hdl.handle.net/1969.1/166485]
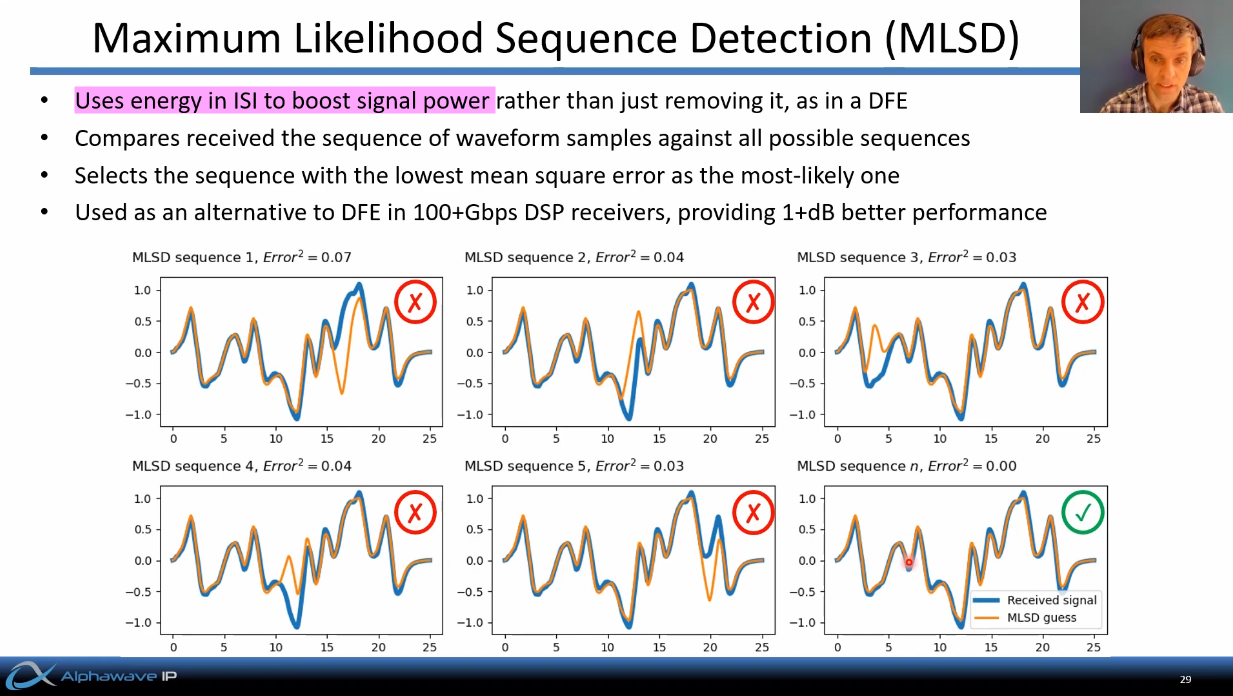
There are several variants of MLSD (Maximum Likelihood Sequence Detection), including:
- Viterbi Algorithm
- Decision Feedback Sequence Estimation (DFSE)
- Soft-Output MLSD
[Evolution Of Equalization Techniques In High-Speed SerDes For Extended Reaches. https://semiengineering.com/evolution-of-equalization-techniques-in-high-speed-serdes-for-extended-reaches/]
Mueller-Muller CDR
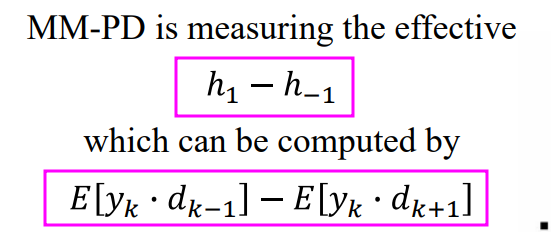
MMPD infers the channel response from baud-rate samples of the received data, the adaptation aligns the sampling clock such that pre-cursor is equal to the post-cursor in the pulse response
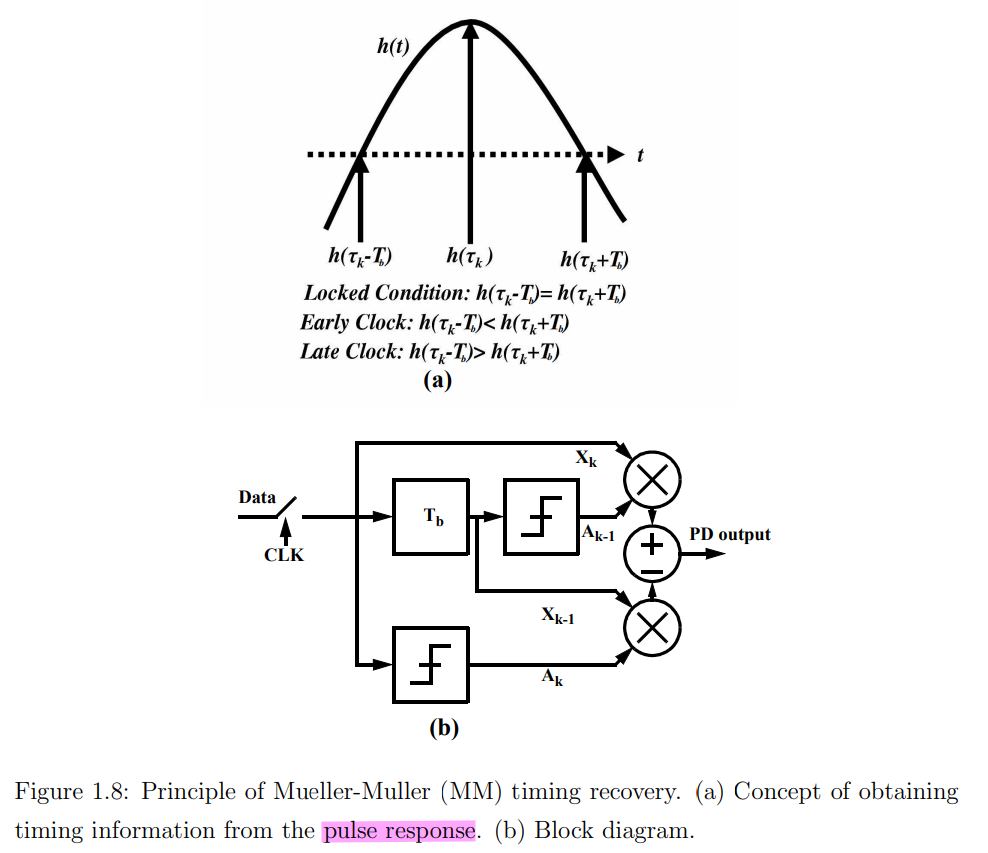
Faisal A. Musa. "HIGH-SPEED BAUD-RATE CLOCK RECOVERY" [https://www.eecg.utoronto.ca/~tcc/thesis-musa-final.pdf]
Faisal A. Musa."CLOCK RECOVERY IN HIGH-SPEED MULTILEVEL SERIAL LINKS" [https://www.eecg.utoronto.ca/~tcc/faisal_iscas03.pdf]
Eduardo Fuentetaja. "Analysis of the M&M Clock Recovery Algorithm" [https://edfuentetaja.github.io/sdr/m_m_analysis/]
Liu, Tao & Li, Tiejun & Lv, Fangxu & Liang, Bin & Zheng, Xuqiang & Wang, Heming & Wu, Miaomiao & Lu, Dechao & Zhao, Feng. (2021). Analysis and Modeling of Mueller-Muller Clock and Data Recovery Circuits. Electronics. 10. 1888. 10.3390/electronics10161888.
Gu, Youzhi & Feng, Xinjie & Chi, Runze & Chen, Yongzhen & Wu, Jiangfeng. (2022). Analysis of Mueller-Muller Clock and Data Recovery Circuits with a Linearized Model. 10.21203/rs.3.rs-1817774/v1.
Baud-Rate CDRs [https://ocw.snu.ac.kr/sites/default/files/NOTE/Lec%206%20-%20Clock%20and%20Data%20Recovery.pdf]
F. Spagna et al., "A 78mW 11.8Gb/s serial link transceiver with adaptive RX equalization and baud-rate CDR in 32nm CMOS," 2010 IEEE International Solid-State Circuits Conference - (ISSCC), San Francisco, CA, USA, 2010, pp. 366-367, doi: 10.1109/ISSCC.2010.5433823.
K. Yadav, P. -H. Hsieh and A. C. Carusone, "Loop Dynamics Analysis of PAM-4 Mueller–Muller Clock and Data Recovery System," in IEEE Open Journal of Circuits and Systems, vol. 3, pp. 216-227, 2022
Jaeduk Han, "Design and Automatic Generation of 60Gb/s Wireline Transceivers" [https://www2.eecs.berkeley.edu/Pubs/TechRpts/2019/EECS-2019-143.pdf]


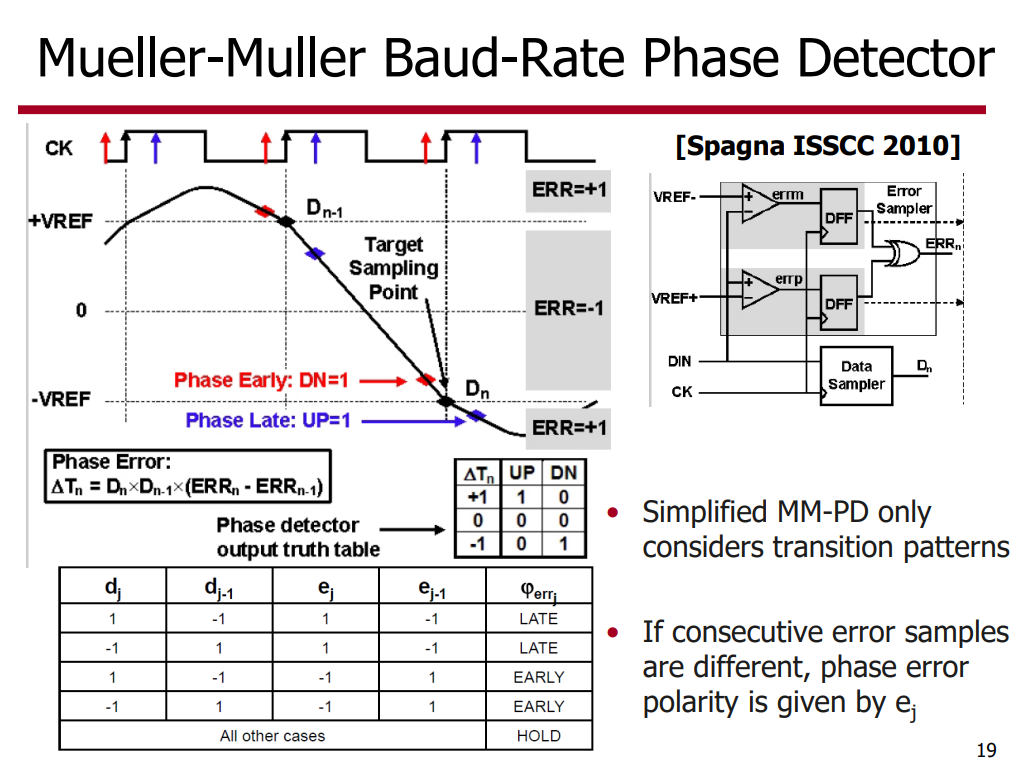

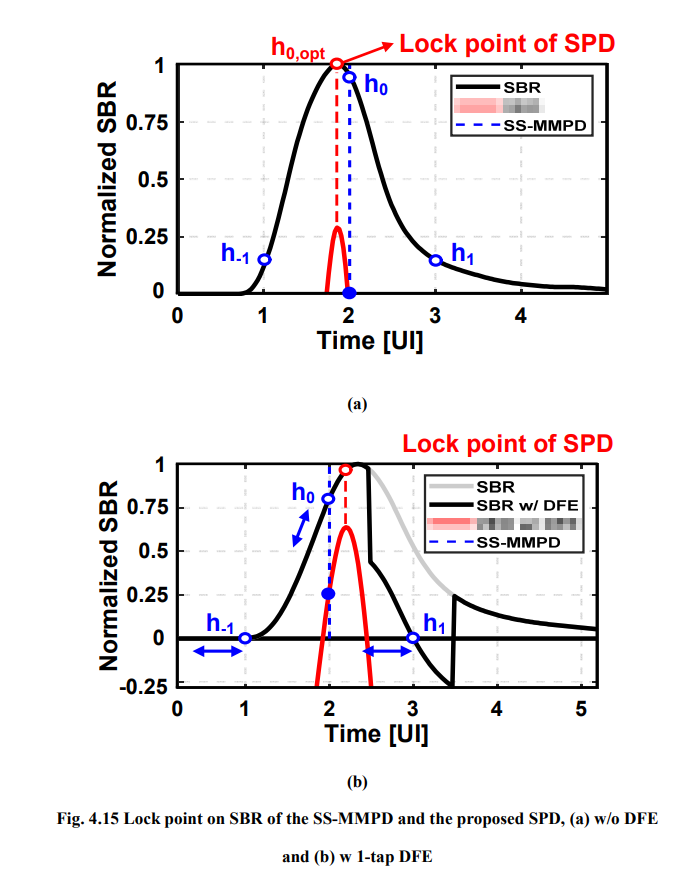
SS-MM CDR

\(h_1\) is necessary
without DFE
SS-MMPD locks at the point (\(h_1=h_{-1}\))
With a 1-tap DFE
1-tap adaptive DFE that forces the \(h_1\) to be zero, the SS-MMPD locks wherever the \(h_{-1}\) is zero and drifts eventually.
Consequently, it suffers from a severe multiple-locking problem with an adaptive DFE
Kwangho Lee, "Design of Receiver with Offset Cancellation of Adaptive Equalizer and Multi-Level Baud-Rate Phase Detector" [https://s-space.snu.ac.kr/bitstream/10371/177584/1/000000167211.pdf]
Pattern filter
| pattern | main cursor |
|---|---|
| 011 | \(s_{011}=-h_1+h_0+h_{-1}\) |
| 110 | \(s_{110}=h_1+h_0-h_{-1}\) |
| 100 | \(s_{100}=h_1-h_0-h_{-1}\) |
| 001 | \(s_{001}=-h_1-h_0+h_{-1}\) |
During adapting, we make
- \(s_{011}\) & \(s_{110}\) are approaching to each other
- \(s_{100}\) & \(s_{001}\) are approaching to each other
Then, \(h_{-1}\) and \(h_1\) are same, which is desired
Bang-Bang CDR
alexander PD or !!PD
The alexander PD locks that edge clock (clkedge) is located at zero crossings of the data. The \(h_{-0.5}\) and \(h_{0.5}\) are equal at the lock point, where the \(h_{-0.5}\) and \(h_{0.5}\) are the cursors located at -0.5 UI and 0.5 UI.
Kwangho Lee, "Design of Receiver with Offset Cancellation of Adaptive Equalizer and Multi-Level Baud-Rate Phase Detector" [https://s-space.snu.ac.kr/bitstream/10371/177584/1/000000167211.pdf]
Shahramian, Shayan, "Adaptive Decision Feedback Equalization With Continuous-time Infinite Impulse Response Filters" [https://tspace.library.utoronto.ca/bitstream/1807/77861/3/Shahramian_Shayan_201606_PhD_thesis.pdf]
MENIN, DAVIDE, "Modelling and Design of High-Speed Wireline Transceivers with Fully-Adaptive Equalization" [https://air.uniud.it/retrieve/e27ce0ca-15f7-055e-e053-6605fe0a7873/Modelling%20and%20Design%20of%20High-Speed%20Wireline%20Transceivers%20with%20Fully-Adaptive%20Equalization.pdf]
reference
Stojanovic, Vladimir & Ho, A. & Garlepp, B. & Chen, Fred & Wei, J. & Alon, Elad & Werner, C. & Zerbe, J. & Horowitz, M.A.. (2004). Adaptive equalization and data recovery in a dual-mode (PAM2/4) serial link transceiver. IEEE Symposium on VLSI Circuits, Digest of Technical Papers. 348 - 351. 10.1109/VLSIC.2004.1346611.
A. A. Bazargani, H. Shakiba and D. A. Johns, "MMSE Equalizer Design Optimization for Wireline SerDes Applications," in IEEE Transactions on Circuits and Systems I: Regular Papers, doi: 10.1109/TCSI.2023.3328807.
Masum Hossain, ISSCC2023 T11: "Digital Equalization and Timing Recovery Techniques for ADC-DSP-based Highspeed Links" [https://www.nishanchettri.com/isscc-slides/2023%20ISSCC/TUTORIALS/T11.pdf]
—, "LOW POWER DIGITAL EQUALIZATION FOR HIGH SPEED SERDES" [https://www.ieeetoronto.ca/wp-content/uploads/2020/06/SSCS_invited_talk.pdf]
A. Sharif-Bakhtiar, A. Chan Carusone, "A Methodology for Accurate DFE Characterization," IEEE RFIC Symposium, Philadelphia, Pennsylvania, June 2018. [PDF] [Slides – PDF]