Oscillators Phase Noise
Phase Noise Definition
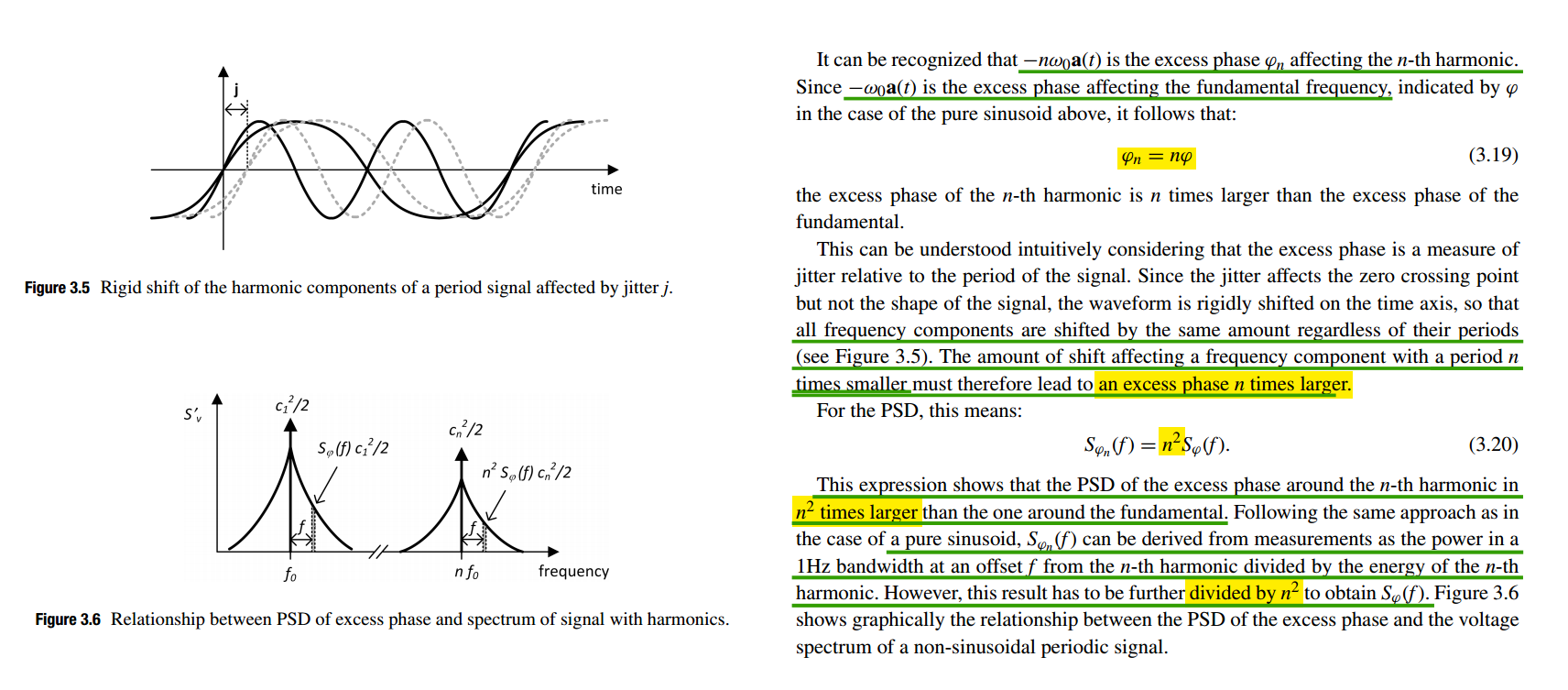
Eq. (3.25) is widely adopted by industry and academia
using the narrow angle assumption, the two definitions above are equivalent
If the narrow angle condition is not satisfied, however, the two definitions differ
PM vs. FM jitter
Deog-Kyoon Jeong. Topics in IC Design: 1.1 Introduction to Jitter [https://ocw.snu.ac.kr/sites/default/files/NOTE/Lec%201%20-%20Jitter%20and%20Phase%20Noise.pdf]
Phase Noise Profile
Power Spectral Density of Brownian Motion despite non-stationary [https://dsp.stackexchange.com/a/75043/59253]
white noise
\(1/f^2\) Phase Noise Profile
Sudhakar Pamarti. CICC 2020 ES2-2: Basics of Closed- and Open-Loop Fractional Frequency Synthesis [https://youtu.be/t1TY-D95CY8?si=tbav3J2yag38HyZx]
flicker noise
\(1/f^3\) Phase Noise Profile
\[ S_{\phi n} = \frac{K}{f}\left(\frac{K_{VCO}}{2\pi f}\right)^2 \propto \frac{1}{f^3} \]
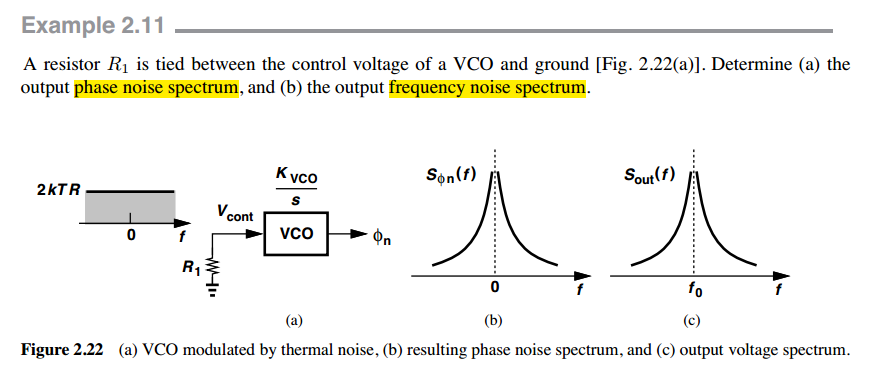
Free-running Oscillator
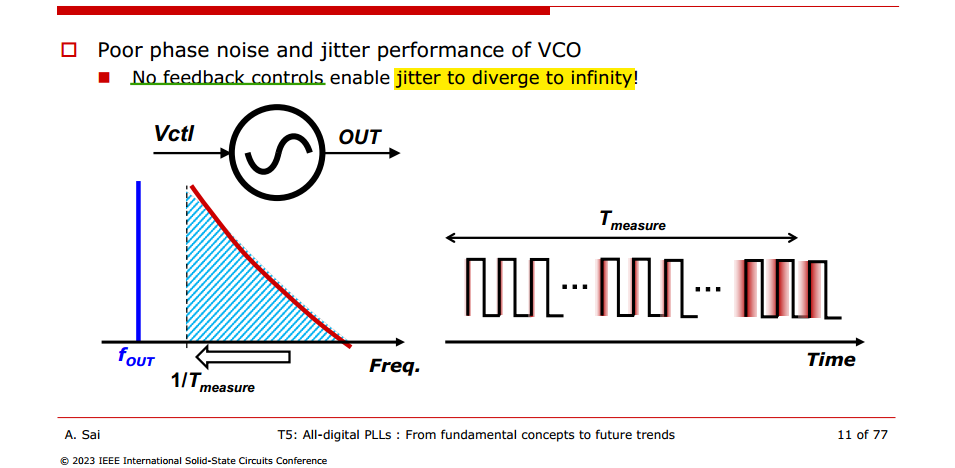
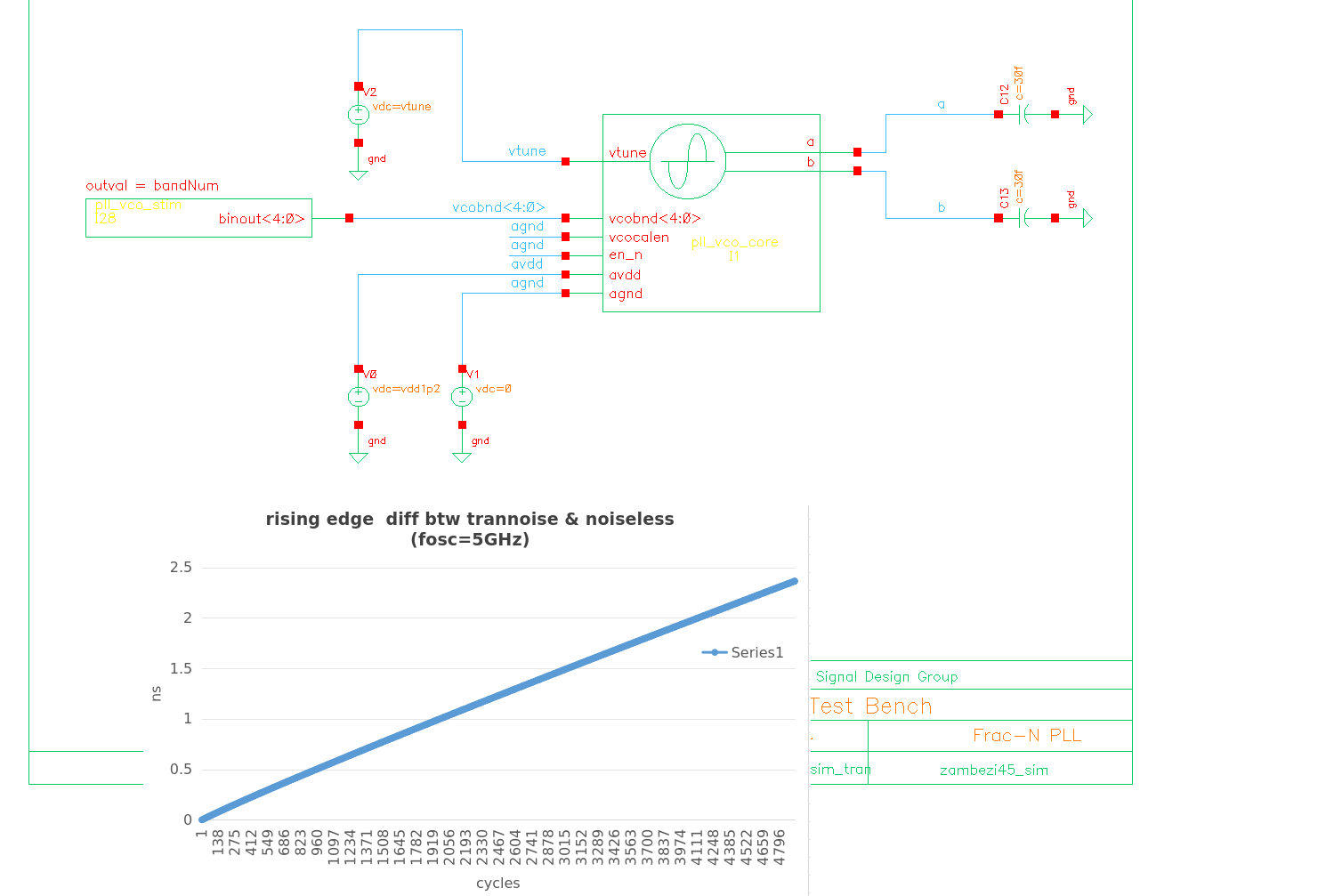
Note that \(f_{min}\) is related to the observation time. The longer we observe the device under test, the smaller \(f_{min}\) must be
Ali Sheikholeslami ISSCC 2008 T5: Basics of Chip-to-Chip and Backplane Signaling [https://www.nishanchettri.com/isscc-slides/2008%20ISSCC/Tutorials/T10_Pres.pdf]
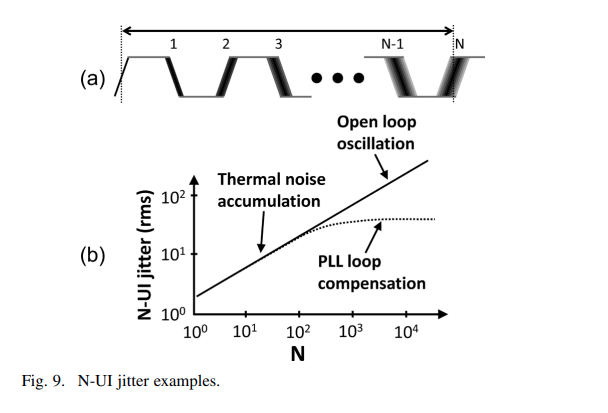
B. Casper and F. O'Mahony, "Clocking Analysis, Implementation and Measurement Techniques for High-Speed Data Links-A Tutorial," in IEEE Transactions on Circuits and Systems I. [https://people.engr.tamu.edu/spalermo/ecen689/clocking_analysis_hs_links_casper_tcas1_2009.pdf]
Lorentzian spectrum
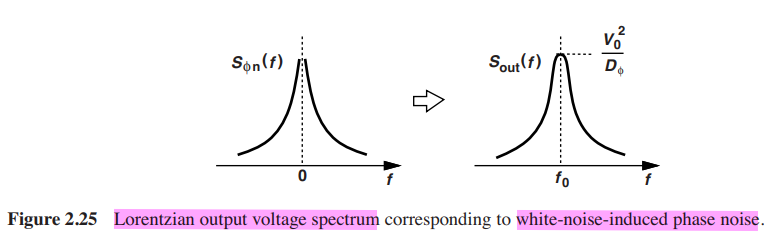
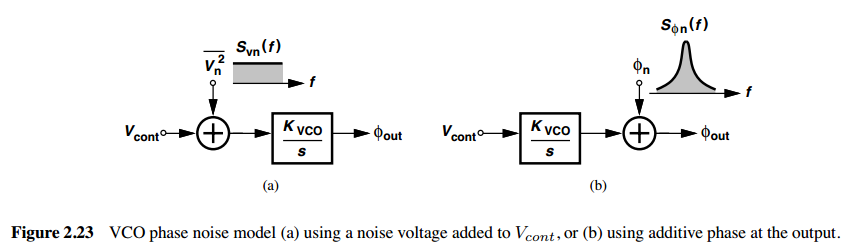
We typically use the two spectra, \(S_{\phi n}(f)\) and \(S_{out}(f)\), interchangeably, but we must resolve these inconsistencies. voltage spectrum is called Lorentzian spectrum
The periodic signal \(x(t)\) can be expanded in Fourier series as:
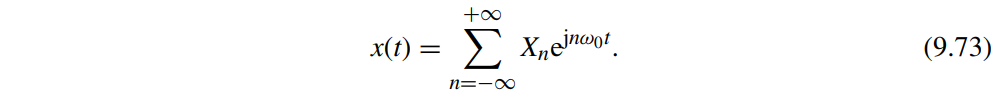
Assume that the signal is subject to excess phase noise, which is modeled by adding a time-dependent noise component \(\alpha(t)\). The noisy signal can be written \(x(t+\alpha(t))\), the added excess phase \(\phi(t)= \frac{\alpha(t)}{\omega_0}\)
The autocorrelation of the noisy signal is by definition:
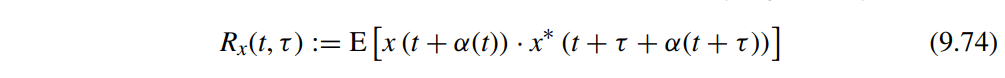
The autocorrelation averaged over time results in:
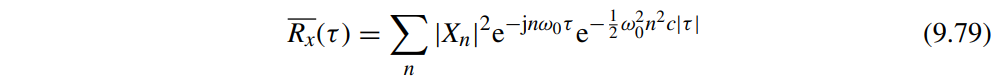
By taking the Fourier transform of the autocorrelation, the spectrum of the signal \(x(t + \alpha(t))\) can be expressed as
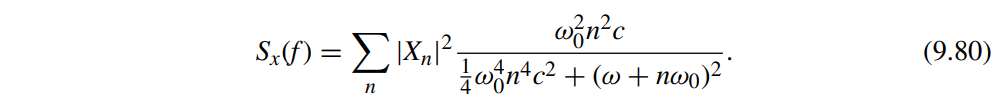
It is also interesting to note how the integral in Equation 9.80 around each harmonic is equal to the power of the harmonic itself \(|X_n|^2\)
The integral \(S_x(f)\) around harmonic is \[\begin{align} P_{x,n} &= \int_{f=-\infty}^{\infty} |X_n|^2\frac{\omega_0^2n^2c}{\frac{1}{4}\omega_0^4n^4c^2+(\omega +n\omega_0)^2}df \\ &= |X_n|^2\int_{\Delta f=-\infty}^{\infty}\frac{2\beta}{\beta^2+(2\pi\cdot\Delta f)^2}d\Delta f \\ &= |X_n|^2\frac{1}{\pi}\arctan(\frac{2\pi \Delta f}{\beta})|_{-\infty}^{\infty} \\ &= |X_n|^2 \end{align}\]
The phase noise does not affect the total power in the signal, it only affects its distribution
- Without phase noise, \(S_v(f)\) is a series of impulse functions at the harmonics of \(f_o\).
- With phase noise, the impulse functions spread, becoming fatter and shorter but retaining the same total power
Phase perturbed by a stationary noise with Gaussian PDF
If keep \(\phi_{rms}\) in \(R_x(\tau)\), i.e. \[ R_x(\tau)=\frac{A^2}{2}e^{-\phi_{rms}^2}\cos(2\pi f_0 \tau)e^{R_\phi(\tau)}\approx \frac{A^2}{2}e^{-\phi_{rms}^2}\cos(2\pi f_0 \tau)(1+R_\phi(\tau)) \] The PSD of the signal is \[ S_x(f) = \mathcal{F} \{ R_x(\tau) \} = \frac{P_c}{2}e^{-\phi_{rms}^2}\left[S_\phi(f+f_0)+S_\phi(f-f_0)\right] + \frac{P_c}{2}e^{-\phi_{rms}^2}\left[\delta(f+f_0)+\delta(f-f_0)\right] \] ❗❗above Eq isn't consistent with stationary white noise process - the following section
Phase perturbed by a stationary WHITE noise process
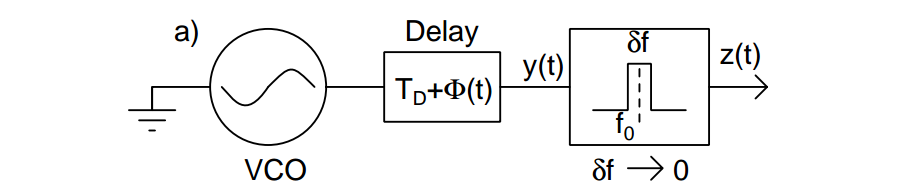
Assuming that the delay line is noiseless
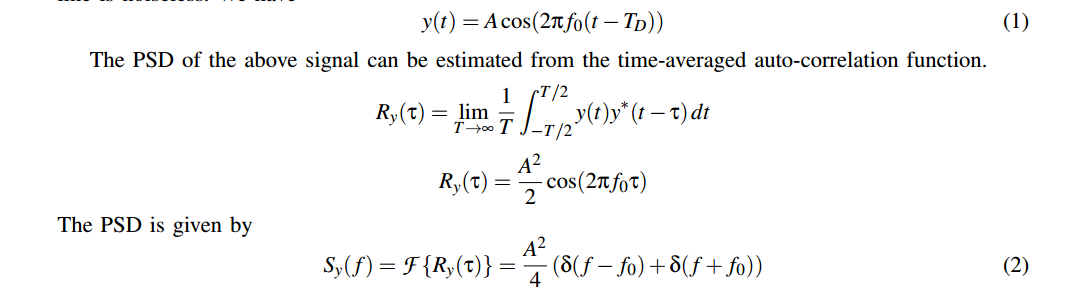
Expanding the cosine function we get \[\begin{align} R_y(t,\tau) &= \frac{A^2}{2}\left\{\cos(2\pi f_0\tau)E[\cos(\phi(t)-\phi(t-\tau))] - \sin(2\pi f_0\tau)E[\sin(\phi(t)-\phi(t-\tau))]\right\} \\ &+ \frac{A^2}{2}\left\{\cos(4\pi f_0(t+\tau/2-T_D))E[\cos(\phi(t)+\phi(t-\tau))] - \sin(4\pi f_0(t+\tau/2-T_D))E[\sin(\phi(t)+\phi(t-\tau))] \right\} \end{align}\]
where, both the process \(\phi(t)-\phi(t-\tau)\) and \(\phi(t)+\phi(t-\tau)\) are independent of time \(t\), i.e. \(E[\cos(\phi(t)+\phi(t-\tau))] = m_{\cos+}(\tau)\), \(E[\cos(\phi(t)-\phi(t-\tau))] = m_{\cos-}(\tau)\), \(E[\sin(\phi(t)+\phi(t-\tau))] = m_{\sin+}(\tau)\) and \(E[\sin(\phi(t)-\phi(t-\tau))] = m_{\sin-}(\tau)\)
we obtain \[\begin{align} R_y(t,\tau) &= \frac{A^2}{2}\left\{\cos(2\pi f_0\tau)m_{\cos-}(\tau) - \sin(2\pi f_0\tau)m_{\sin-}(\tau)\right\} \\ &+ \frac{A^2}{2}\left\{\cos(4\pi f_0(t+\tau/2-T_D))m_{\cos+}(\tau) - \sin(4\pi f_0(t+\tau/2-T_D))m_{\sin+}(\tau) \right\} \end{align}\]
The second term in the above expression is periodic in \(t\) and to estimate its PSD, we compute the
time-averaged autocorrelation function \[
R_y(\tau) = \frac{A^2}{2}\left\{\cos(2\pi f_0\tau)m_{\cos-}(\tau) -
\sin(2\pi f_0\tau)m_{\sin-}(\tau)\right\}
\] 
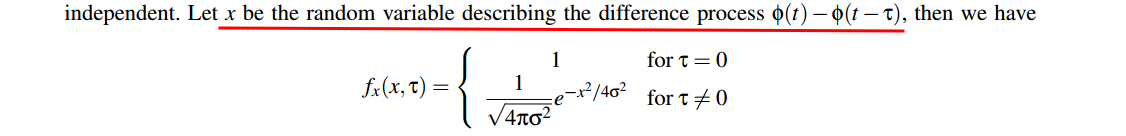
After nontrivial derivation
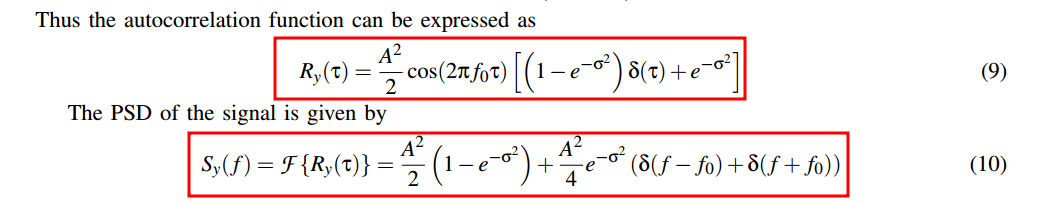
Phase perturbed by a Weiner process
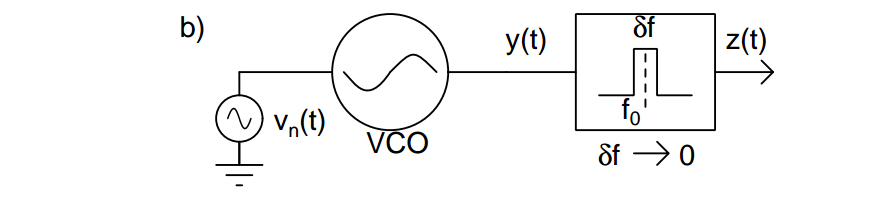
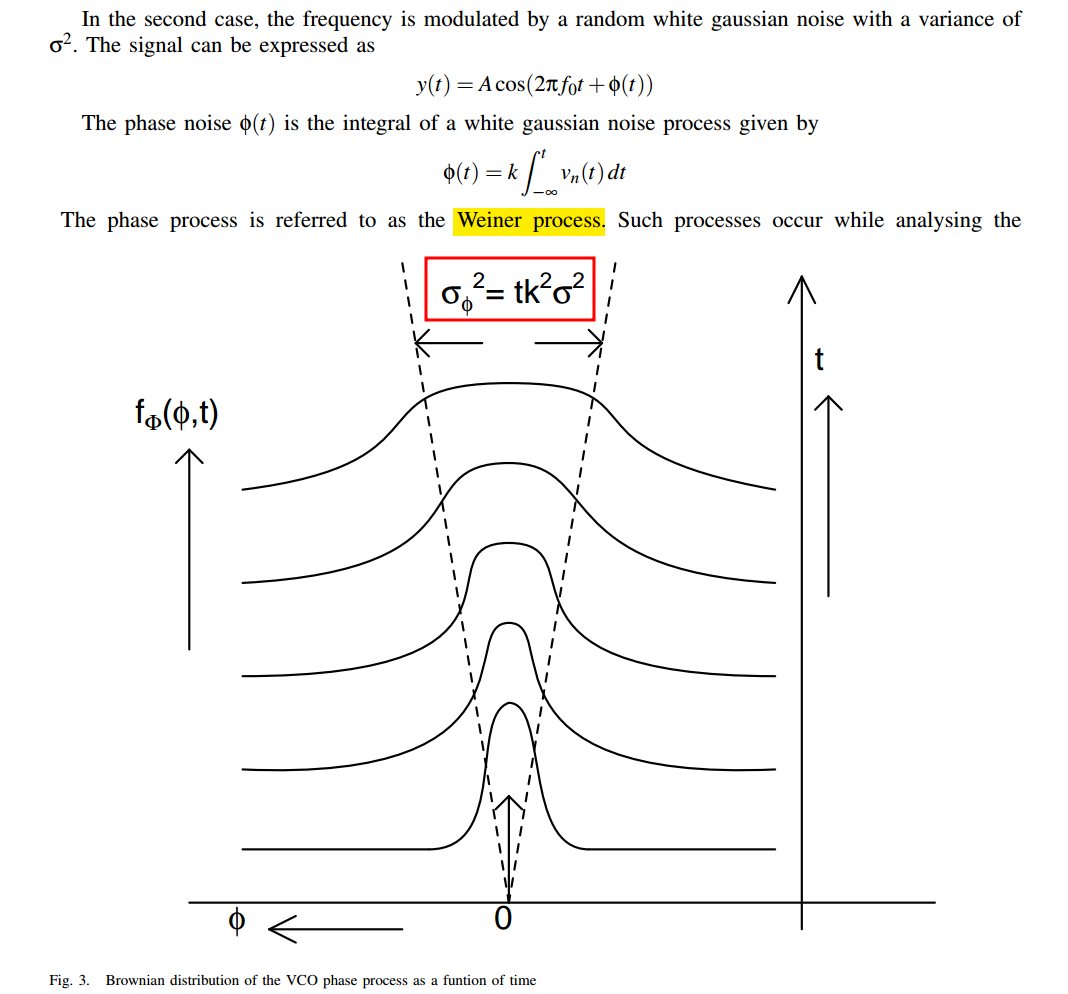
The phase process \(\phi(t)\) is also gaussian but with an increasing variance which grows linearly with time \(t\)
\[\begin{align} R_y(t,\tau) &= \frac{A^2}{2}\left\{\cos(2\pi f_0\tau)E[\cos(\phi(t)-\phi(t-\tau))] - \sin(2\pi f_0\tau)E[\sin(\phi(t)-\phi(t-\tau))]\right\} \\ &+ \frac{A^2}{2}\left\{\cos(4\pi f_0(t+\tau/2-T_D)E[\cos(\phi(t)+\phi(t-\tau))] - \sin(4\pi f_0(t+\tau/2-T_D)E[\sin(\phi(t)+\phi(t-\tau))] \right\} \end{align}\]
The spectrum of \(y(t)\) is determined by the asymptotic behavior of \(R_y(t,\tau)\) as \(t\to \infty\)
❗❗ \(\lim_{t\to\infty}R_y(t,\tau)\) rather than time-averaged autocorrelation function of cyclostationary process, ref. Demir's paper
We define \(\zeta(t, \tau)=\phi(t)+\phi(t-\tau) = \phi(t)-\phi(t-\tau) + 2\phi(t-\tau)\), the expected value of \(\zeta(t,\tau)\) is 0, the variance is \(\sigma_{\zeta}^2=(k\sigma)^2(\tau + 4(t-\tau))=(k\sigma)^2(4t-3\tau)\) \[ E[\cos(\zeta(t,\tau))]=\frac{1}{\sqrt{2\pi \sigma_{\zeta}^2}}\int_{-\infty}^{\infty}e^{-\zeta^2/2\sigma_{\zeta}^2}\cos(\zeta)d\zeta = e^{-\sigma_{\zeta}^2/2}=e^{-(k\sigma)^2(4t-\tau)} \] i.e., \(\lim _{t\to \infty} E[\cos(\zeta(t,\tau))] = \lim_{t\to \infty}e^{-(k\sigma)^2(4t-\tau)} = 0\)
For \(E[\sin(\zeta(t,\tau))]\), we have \[ E[\sin(\zeta(t,\tau))] = \frac{1}{\sqrt{2\pi \sigma_{\zeta}^2}}\int_{-\infty}^{\infty}e^{-\zeta^2/2\sigma_{\zeta}^2}\sin(\zeta)d\zeta \] i.e., \(E[\sin(\zeta(t,\tau))]\) is odd function, therefore \(E[\sin(\zeta(t,\tau))]=0\)
Finally, we obtain
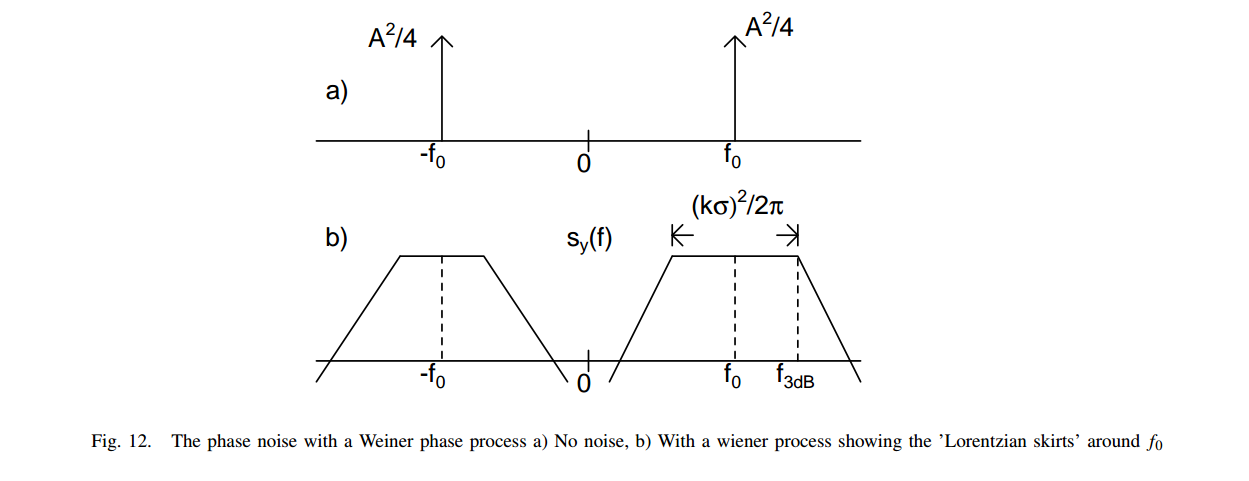
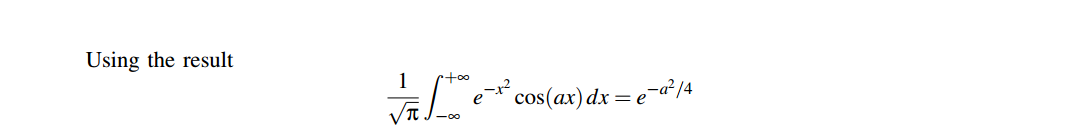
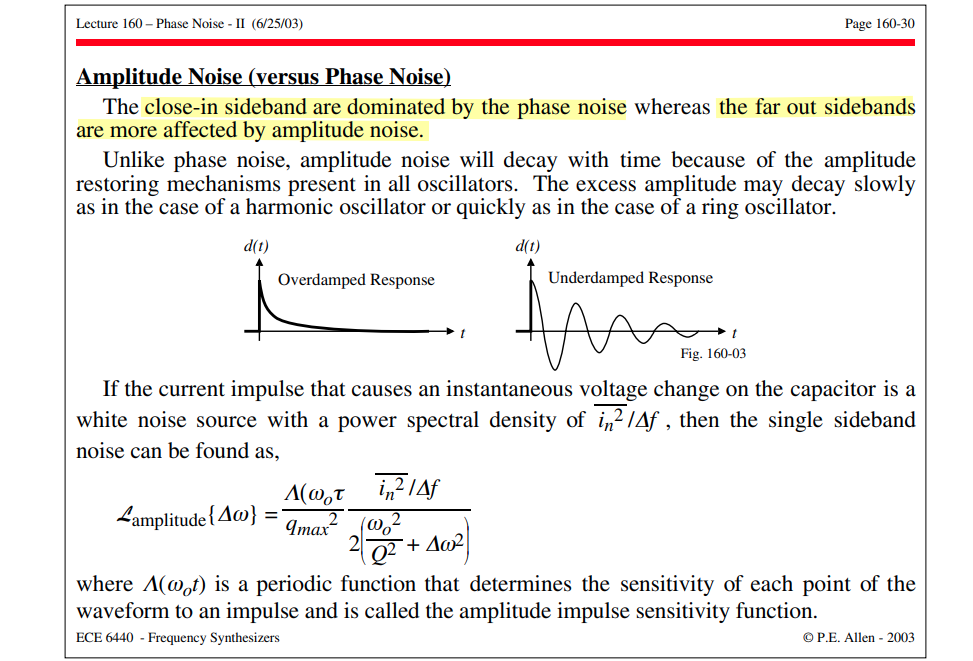
Amplitude Noise
P.E. Allen - 2003. ECE 6440 - Frequency Synthesizers: Lecture 160 – Phase Noise - II [https://pallen.ece.gatech.edu/Academic/ECE_6440/Summer_2003/L160-PhNoII(2UP).pdf]
reference
A. Hajimiri and T. H. Lee, "A general theory of phase noise in electrical oscillators," in IEEE Journal of Solid-State Circuits, vol. 33, no. 2, pp. 179-194, Feb. 1998 [paper], [slides]
—, "Corrections to "A General Theory of Phase Noise in Electrical Oscillators"" [https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=678662]
—, RFIC2024 "Noise in Oscillators from Understanding to Design"
Carlo Samori, "Phase Noise in LC Oscillators: From Basic Concepts to Advanced Topologies" [https://www.ieeetoronto.ca/wp-content/uploads/2020/06/DL-VCO-short.pdf]
—, "Understanding Phase Noise in LC VCOs: A Key Problem in RF Integrated Circuits," in IEEE Solid-State Circuits Magazine, vol. 8, no. 4, pp. 81-91, Fall 2016 [https://picture.iczhiku.com/resource/eetop/whIgTikLswaaTVBv.pdf]
—, ISSCC2016, "Understanding Phase Noise in LC VCOs"
Antonio Liscidini, ESSCIRC 2019 Tutorials: Phase Noise in Wireless Applications [https://youtu.be/nGmQ0JdoSE4]
A. Demir, A. Mehrotra and J. Roychowdhury, "Phase noise in oscillators: a unifying theory and numerical methods for characterization," in IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, vol. 47, no. 5, pp. 655-674, May 2000 [https://sci-hub.se/10.1109/81.847872]
Dalt, Nicola Da and Ali Sheikholeslami. "Understanding Jitter and Phase Noise: A Circuits and Systems Perspective." (2018) [https://picture.iczhiku.com/resource/eetop/WykRGJJoHQLaSCMv.pdf]
F. L. Traversa, M. Bonnin and F. Bonani, "The Complex World of Oscillator Noise: Modern Approaches to Oscillator (Phase and Amplitude) Noise Analysis," in IEEE Microwave Magazine, vol. 22, no. 7, pp. 24-32, July 2021 [https://iris.polito.it/retrieve/handle/11583/2903596/e384c433-b8f5-d4b2-e053-9f05fe0a1d67/MM%20noise%20-%20v5.pdf]
Poddar, Ajay & Rohde, Ulrich & Apte, Anisha. (2013). How Low Can They Go?: Oscillator Phase Noise Model, Theoretical, Experimental Validation, and Phase Noise Measurements. Microwave Magazine, IEEE. [http://time.kinali.ch/rohde/noise/how_low_can_they_go-2013-poddar_rohde_apte.pdf]
Pietro Andreani, "RF Harmonic Oscillators Integrated in Silicon Technologies" [https://www.ieeetoronto.ca/wp-content/uploads/2020/06/DL-Toronto.pdf]
Chembiyan T, "Brownian Motion And The Oscillator Phase Noise" [link]
—, "Jitter and Phase Noise in Oscillators" [link]
—, "Jitter and Phase Noise in Phase Locked Loops" [link]
—, "PLLs and reference spurs" [link]
Godone, A. & Micalizio, Salvatore & Levi, Filippo. (2008). RF spectrum of a carrier with a random phase modulation of arbitrary slope. [https://sci-hub.se/10.1088/0026-1394/45/3/008]
Bae, Woorham; Jeong, Deog-Kyoon: 'Analysis and Design of CMOS Clocking Circuits for Low Phase Noise' (Materials, Circuits and Devices, 2020)