Signaling for Data Converter
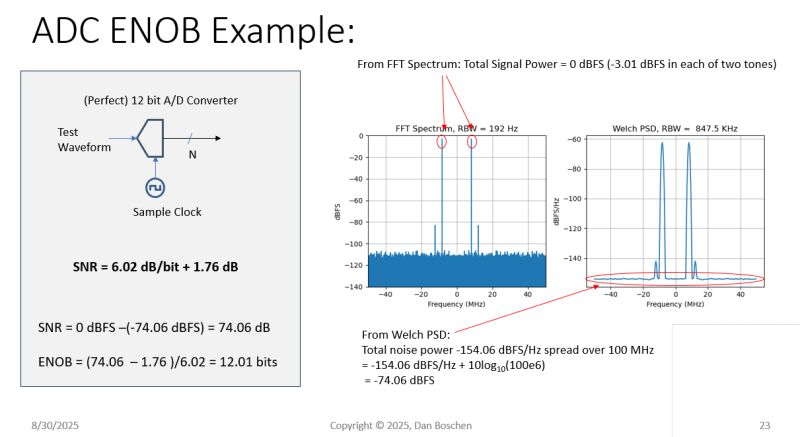
ADC ENOB
Dan Boschen, GRCon25: Quantifying Signal Quality: Practical Tools for High-Fidelity Waveform Analysis
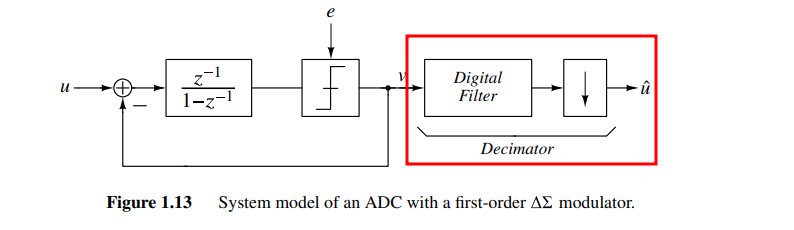
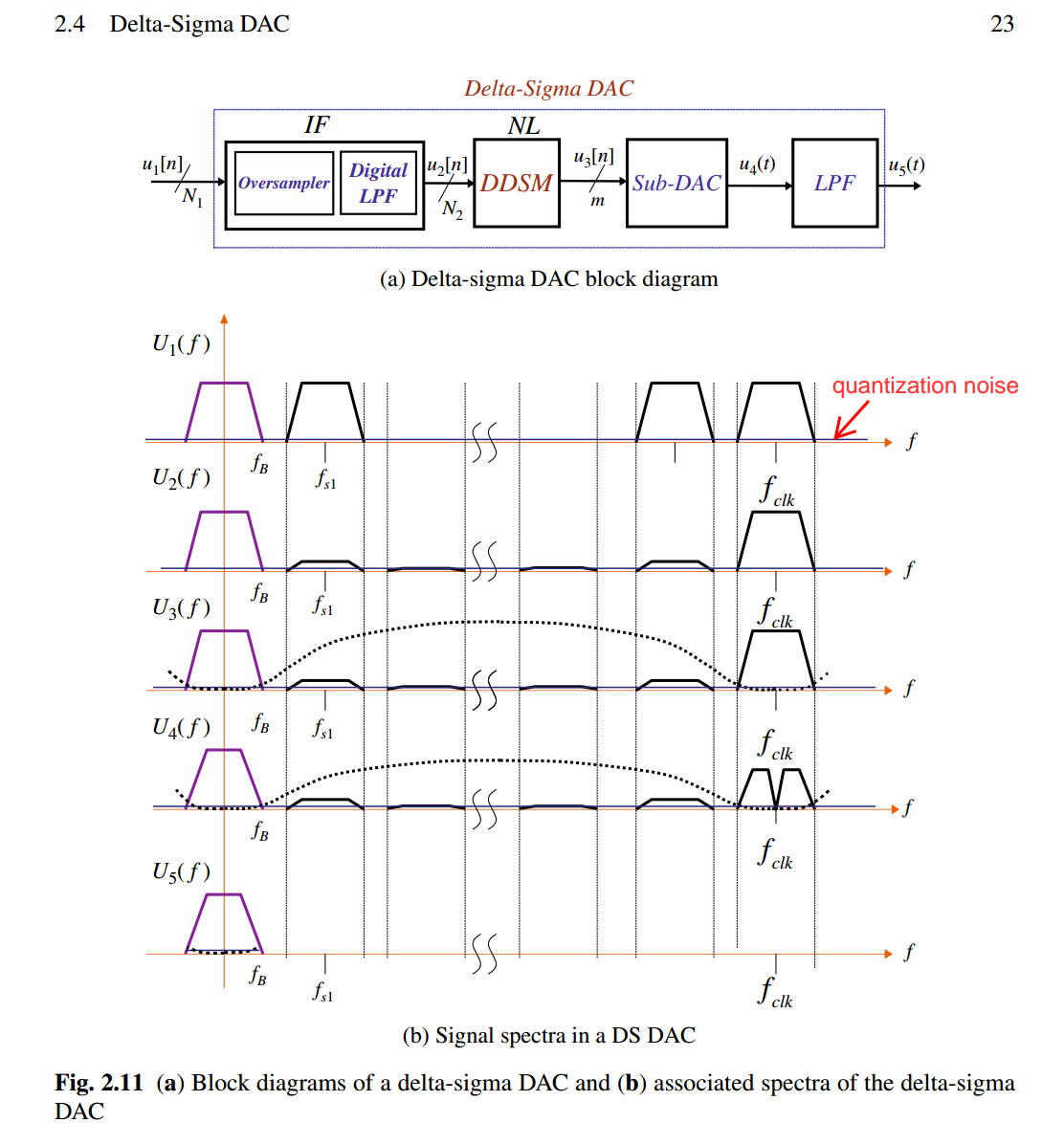
decimation filter
[https://web.engr.oregonstate.edu/~temes/ece627/Lecture_Notes/First_Order_DS_ADC_scan1.pdf]
[https://web.engr.oregonstate.edu/~temes/ece627/Lecture_Notes/First_Order_DS_ADC_scan2.pdf]
The combination of the the digital post-filter and downsampler is called the decimation filter or decimator
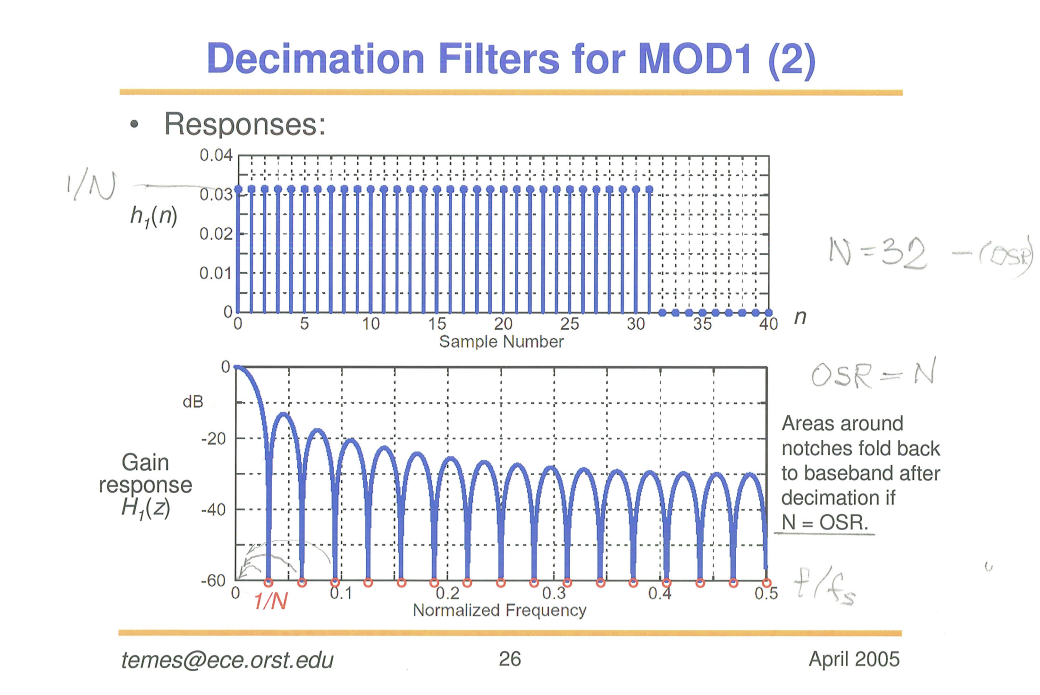
\(\text{sinc}\) filter

Suppose \(T=1\) \[ H_1(e^{j2\pi f}) = \frac{\text{sinc}(Nf)}{\text{sinc}(f)} = \frac{1}{N}\frac{\sin(\pi Nf)}{\sin(\pi f)} \] that is \(\lim_{f\to 0^+}H_1(e^{j2\pi f}) = 1\) and \(H_1 = 0\) when \(f=\frac{n}{N}, n\in \mathbb{Z}\)
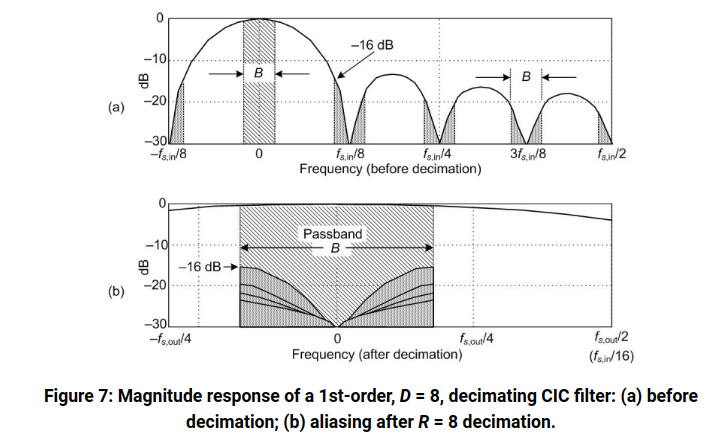
A Beginner's Guide To Cascaded Integrator-Comb (CIC) Filters [https://www.dsprelated.com/showarticle/1337.php]
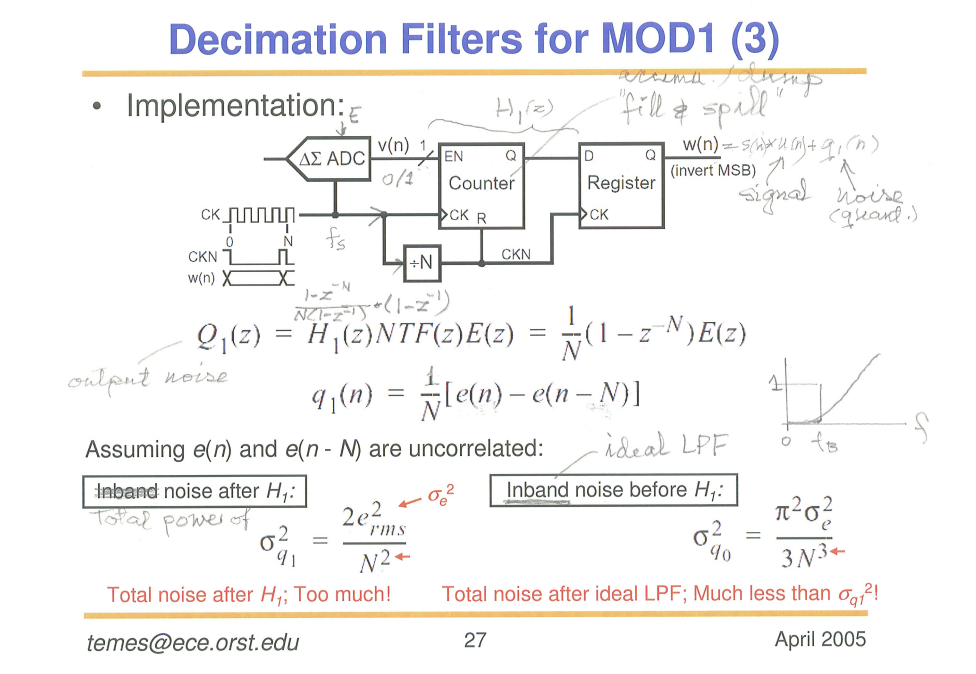
\[ |H_1(\omega)|^2 = \left|\frac{1}{N}(1-e^{-j\omega N}) \right| = \frac{2}{N^2}(1-\cos (\omega N)) \] Total noise after \(H_1\) \[ \sigma_{q_1}^2 = 2\int_0^\pi \frac{e^2_{rms}}{2\pi}\cdot |H_1(\omega)|^2d\omega = \frac{2e^2_{rms}}{N^2} \] inband noise before \(H_1\), i.e. ideal LPF with cutoff frequency \(\frac{\pi}{N}\) \[ \sigma_{q_0}^2 = 2\int_0^{\pi/N}\frac{e_{rms}^2}{2\pi}|1-e^{-j\omega}|^2d\omega = \frac{2e_{rms}^2}{\pi}\left(\frac{\pi}{N}-\sin\frac{\pi}{N}\right) \] with Taylor series \(\sin\frac{\pi}{N}\approx \frac{\pi}{N}-\frac{1}{6}\frac{\pi^3}{N^3}\) \[ \sigma_{q_0}^2 \approx \frac{\pi^2}{3N^3}e_{rms}^2 \]
Taylor’s Series of \(\sin x\) [pdf]
\(\text{sinc}^2\) filter

interpolation filter
Notice that the requirements of the first stage are very demanding
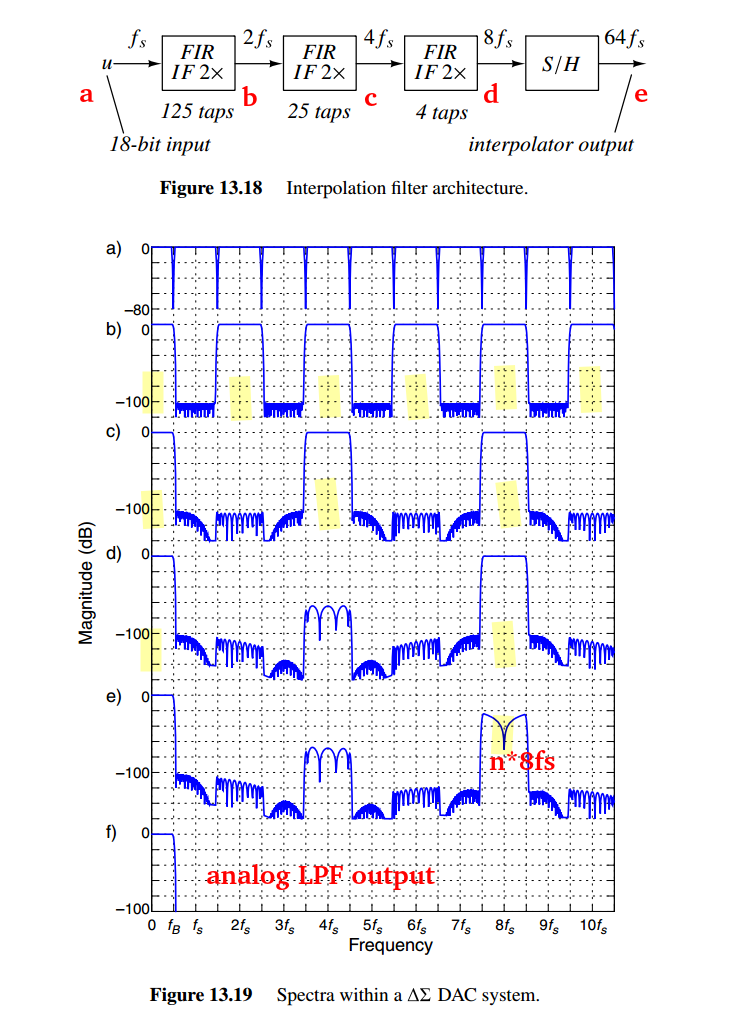
replicas suppression
The spectrum of the high resolution digital signal \(u_1\) contains the original baseband portion and its replicas located at integer multiples of \(f_{s1}\), plus a small amount of quantization noise shown as a solid line

Nigel Redmon [https://dsp.stackexchange.com/a/63438/59253]
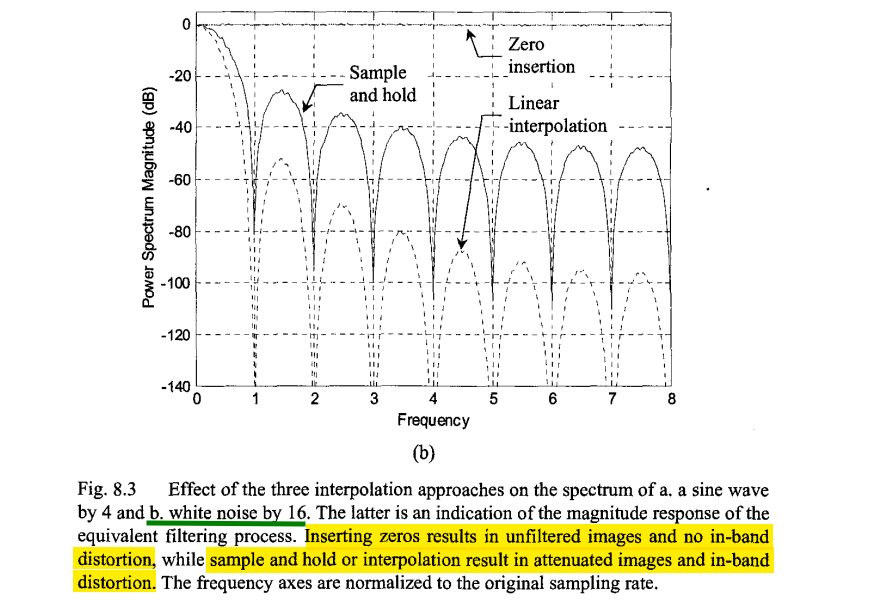
Inserting zeros changes nothing except what we consider the sample rate
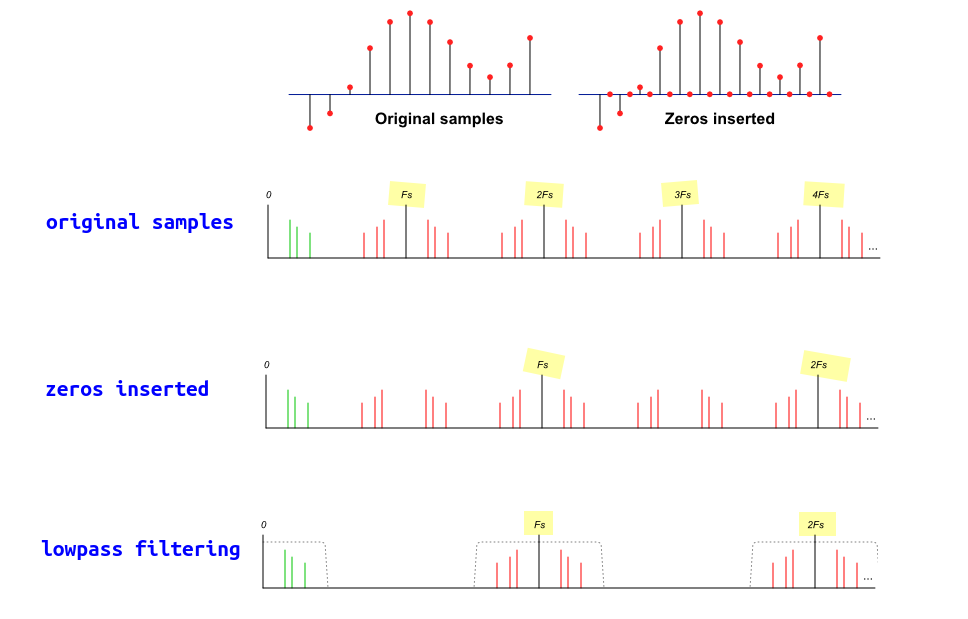

Dan Boschen [https://dsp.stackexchange.com/a/32130/59253]

Bourdopoulos, G. I. (2003). Delta-Sigma modulators : modeling, design and applications. Imperial College Press. [pdf]
DC Gain in Interpolation Filtering
[https://raytroop.github.io/2025/06/21/data-converter-in-action/#dac-zoh]
DC gain is used to compensate the ratio of sampling rate before and after upsample
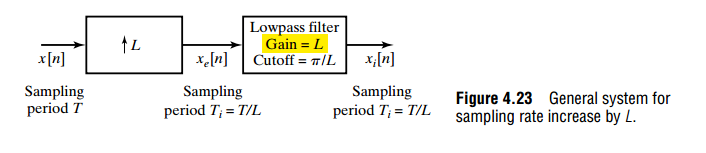
Given \[ X_e = X = \propto \frac{1}{T} = \frac{1}{L\cdot T_i} \] Then, the lowpass filter (ZOH, FOH .etc) gain shall be \(L\)
Employ definition of DTFT, \(X(e^{j\hat{\omega}}) =\sum_{n=-\infty}^{+\infty}x[n]e^{-j\hat{\omega} n}\), and set \(\hat{\omega} = 0\) \[ X(e^{j0}) = \sum_{n=-\infty}^{+\infty}x[n] \] That is, \(\sum_{n=-\infty}^{+\infty}x[n] = \sum_{n=-\infty}^{+\infty}x_e[n]\), so \[ \overline{x_e[n]} = \frac{1}{L} \overline{x[n]} \] It also indicate that dc gain of upsampling is \(1/L\)
ZOH
Zero-Order Hold (ZOH)

dc gain = \(N\)
FOH
First-Order Hold (FOH)

dc gain = \(N\)
reference
Neil Robertson, Model a Sigma-Delta DAC Plus RC Filter [https://www.dsprelated.com/showarticle/1642.php]
—, Modeling a Continuous-Time System with Matlab [https://www.dsprelated.com/showarticle/1055.php]
—, Modeling Anti-Alias Filters [https://www.dsprelated.com/showarticle/1418.php]
—, DAC Zero-Order Hold Models [https://www.dsprelated.com/showarticle/1627.php]
—, “A Simplified Matlab Function for Power Spectral Density”, DSPRelated.com, March, 2020, [https://www.dsprelated.com/showarticle/1333.php]
Arash Loloee, Ph.D. Exploring Decimation Filters [https://www.highfrequencyelectronics.com/Archives/Nov13/1311_HFE_decimationFilters.pdf]
Venkatesh Srinivasan, ISSCC 2019 T5: Noise Shaping in Data Converters
Nan Sun,IEEE CAS 2020: Break the kT/C Noise Limit [https://www.facebook.com/ieeecas/videos/break-the-ktc-noise-limit/322899188976197/]
Yun-Shiang Shu, ISSCC 2022 T3: Noise-Shaping SAR ADCs
Xiyuan Tang, CICC 2025 ES2-1: Noise-Shaping SAR ADCs - From Fundamentals to Recent Advances
Qasim Chaudhari. On Analog-to-Digital Converter (ADC), 6 dB SNR Gain per Bit, Oversampling and Undersampling [https://wirelesspi.com/on-analog-to-digital-converter-adc-6-db-snr-gain-per-bit-oversampling-and-undersampling/]
Pavan, Shanthi, Richard Schreier, and Gabor Temes. (2016) 2016. Understanding Delta-Sigma Data Converters. 2nd ed. Wiley.