Link Models

Posted on Edited on In

Time domain modeling

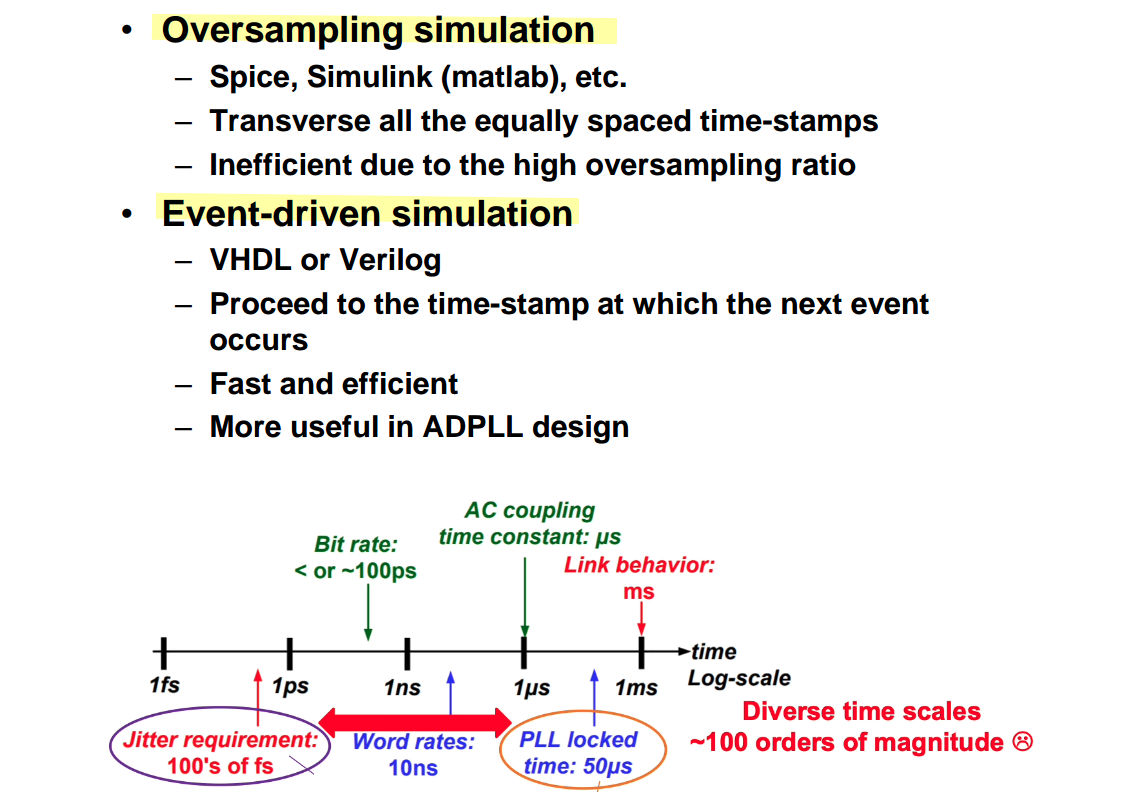
While many different analysis methods exist, including frequency and statistical analysis, time domain results remain the final sign-off

image-20260127221606934

serdespy

Richard Barrie. serdespy — A python library for system-level SerDes modelling and simulation [https://github.com/richard259/serdespy]

python 3.10, samplerate

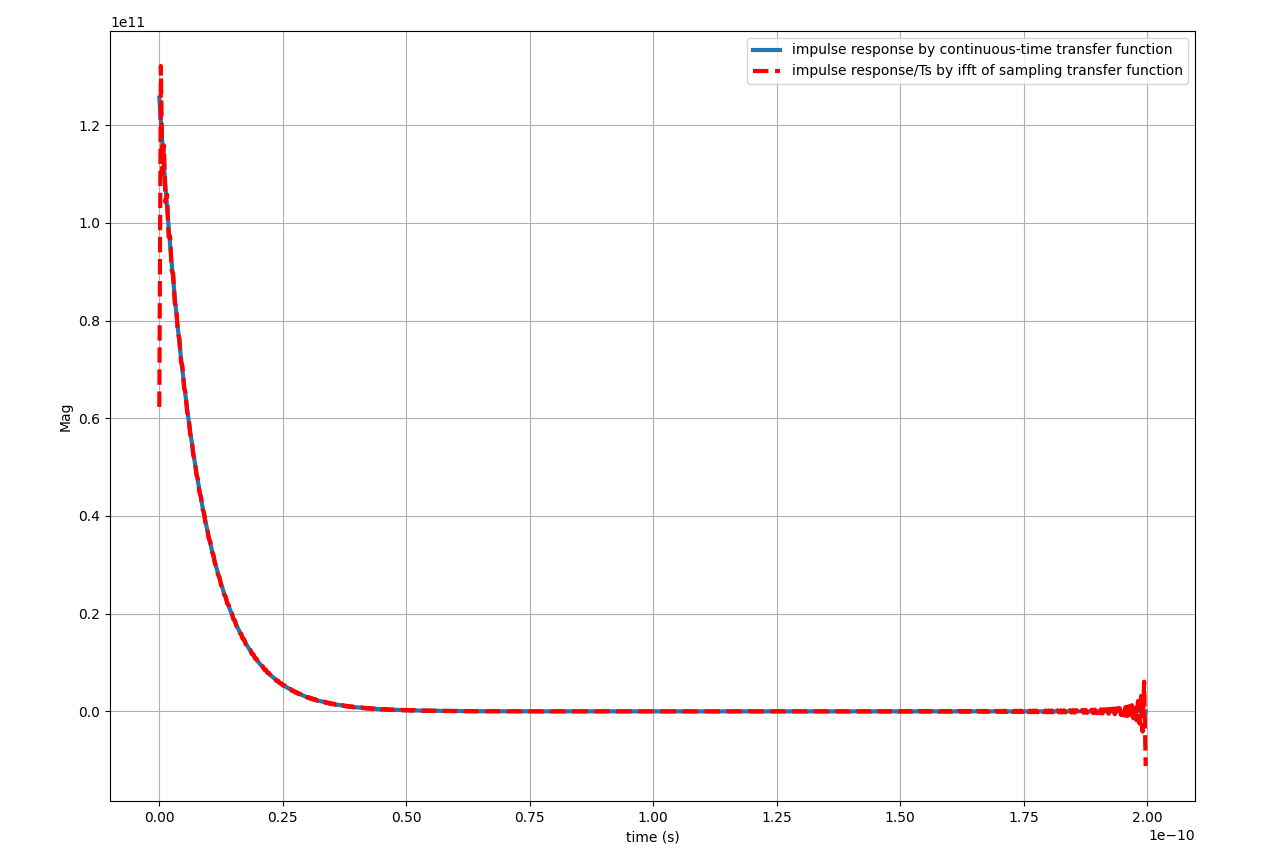
ifft of sampling continuous-time transfer function

freq2impulse.drawio

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def freq2impulse(H, f):
    #Returns the impulse response, h, and (optionally) the step response,
    #hstep, for a system with complex frequency response stored in the array H
    #and corresponding frequency vector f.  The time array is
    #returned in t.  The frequency array must be linearly spaced.

    Hd = np.concatenate((H,np.conj(np.flip(H[1:H.size-1]))))
    h = np.real(np.fft.ifft(Hd))
    #hstep = sp.convolve(h,np.ones(h.size))
    #hstep = hstep[0:h.size]
    t= np.linspace(0,1/f[1],h.size+1)
    t = t[0:-1]

    return h,t

Maybe, the more straightforward method is sampling impulse response of continuous-time transfer function directly

image-20251127200007941

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

fbw = 20e9
wbw = fbw * 2 * np.pi
samples_per_symbol = 64
UI = 1/50e9
Ts = UI/samples_per_symbol
fs = 1/Ts
ws = fs * 2 * np.pi
ttot = 4/fbw # heuristic
N = int(0.5 * fs * ttot)+1
w, H = signal.freqs([1], [1/wbw, 1], np.linspace(0, 0.5*ws, N))

## freq2impulse(H, f), ifft - using sample of continuous-time tranfer function
f = w/(2*np.pi)
Hd = np.concatenate((H,np.conj(np.flip(H[1:H.size-1]))))
hd = np.real(np.fft.ifft(Hd))
t= np.linspace(0,1/f[1],hd.size+1)
t = t[0:-1]

## continuous-time transfer function - impulse
t, hc = signal.impulse(([1], [1/wbw, 1]), T = t)

## hd(kTs) = Ts*hc(kTs)
plt.figure(figsize = (14,10))
plt.plot(t, hc, t, hd/Ts, '--r', linewidth=3)
plt.grid(); plt.legend(['impulse response by continuous-time transfer function','impulse response/Ts by ifft of sampling transfer function'])
plt.ylabel('Mag'); plt.xlabel('time (s)'); plt.show()

JLSD

Kevin Zheng. JLSD — Julia SerDes [https://github.com/kevjzheng/JLSD]

boundary conditions internally, remembering states from the previous (sub-)block

1
2
out = conv(ir, vbits)*tui/osr
lines(tt, out[1:length(vbits)])

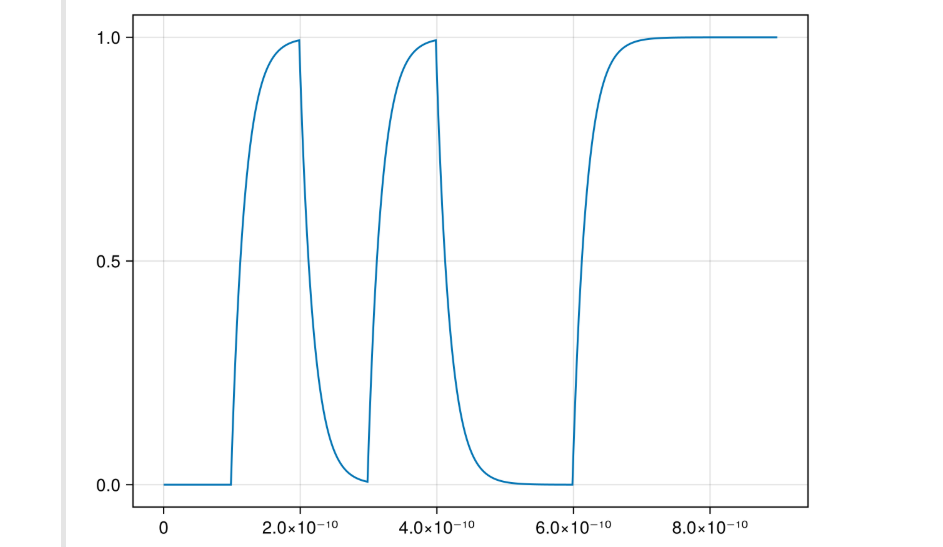
image-20251201003243976

1
2
3
4
5
6
7
8
9
10
11
12
#call our convolution function; let's keep the input memory zero for now
#change the drv parameters in the struct definition to see the waveform/eye change
u_conv!(drv.Vo_conv, Vosr, drv.ir, Vi_mem=zeros(1), gain = drv.swing * param.dt);


#we will also create a non-mutating u_conv function for other uses
function u_conv(input, ir; Vi_mem = zeros(1), gain = 1)
    vconv = gain .* conv(ir, input)
    vconv[eachindex(Vi_mem)] += Vi_mem

    return vconv
end

image-20260127222632389

Kronecker product to create oversampled waveform

1
2
3
4
5
6
7
8
9
function gen_wvfm(bits; tui, osr)
	#helper function used to generate oversampled waveform
	
	Vbits = kron(bits, ones(osr)) #Kronecker product to create oversampled waveform
	dt = tui/osr
	tt = 0:dt:(length(Vbits)-1)*dt

	return tt, Vbits
end

osr.drawio

normalized to the time step \[ \frac{\alpha}{s+\alpha} \overset{\mathcal{L}^{-1}}{\longrightarrow} \alpha\cdot e^{-\alpha t} \]

The integral of impulse response of low pass RC filter \(\int_{0}^{+\infty} \alpha\cdot e^{-\alpha t}dt = 1\) — sum(ir*dt)

1
2
3
4
5
6
7
8
9
10
11
function gen_ir_rc(dt,bw,t_len)
	#helper function that directly calculates a first order RC response, normalized to the time step
    tt = [0:dt:t_len-dt;]

	#checkout the intuitive symbols!
    ω = (2*π*bw)
    ir = ω*exp.(-tt*ω)
    ir .= ir/sum(ir*dt)

    return ir
end

sum(ir)*dt = 1, i.e. the step response 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
using Plots
using LaTeXStrings

tui = 1/10e9;
tlen_ir = 20*tui;


osr_list = [4, 8, 16, 32, 64, 128, 256, 512, 1024];
bw_ir = 8e9;

ω = (2*π*bw_ir);

ir_dt_sum_list = [];

for osr_cur in osr_list
    dt = tui/osr_cur; # Simulation time step
    tt = [0:dt:tlen_ir-dt;]
    ir = ω*exp.(-tt*ω);
    ir_dt_sum = sum(ir*dt);
    push!(ir_dt_sum_list, ir_dt_sum)
end

println(ir_dt_sum_list)
# Any[1.756575097878581, 1.3468434968519964, 1.1652908056870317, 1.0805951388547221, 1.0397838972257087, 1.0197634612560418, 1.0098496044545267, 1.0049167704129547, 1.0024563772359665]

p = plot(osr_list, ir_dt_sum_list, label = "OSR")
gui(p)

image-20251008131325508

generate PAM symbols

here Big Endian

1
2
3
4
5
#generate PAM symbols
   fill!(So, zero(Float64)) #reset So to all 0
   for n = 1:bits_per_sym
       @. So = So + 2^(bits_per_sym-n)*So_bits[n:bits_per_sym:end]
   end
1
2
3
4
5
6
function int2bits(num, nbit)
    return [Bool((num>>k)%2) for k in nbit-1:-1:0]
end


 Si_bits .= vec(stack(int2bits.(Si, bits_per_sym)))

Detailed Transmitter

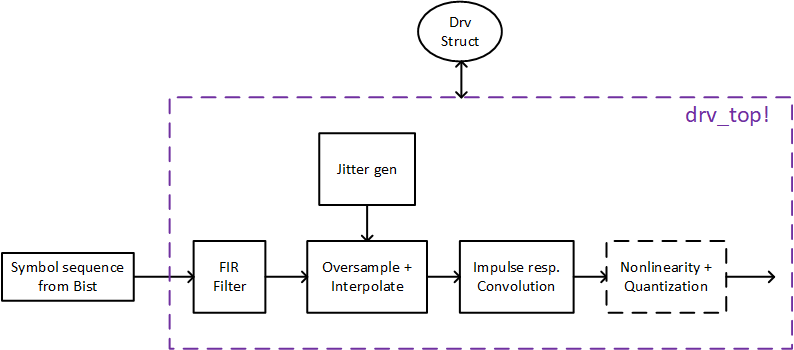
tx blk diagram

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
function drv_top!(drv, input)
	@unpack all parameters and vectors

    apply_fir_filter!(Sfir, input, fir, kwargs...)

	oversample!(Vfir,Sfir)

	if jitter_en
        # !!! jitter gen before impulse response convolution
        # !!! jitter information at each edge location
		add_jitter!(drv, Vfir)
	end
	
    # impulse response of the driver (and subsequent channel, RX front end, etc.) plays a crucial role 
    # in low-pass filtering the jittered waveform to give it a "smoother look"
	convolve!(Vo_conv, Vfir, ir, kwargs...)

end

img

image-20251216231344142

1
2
3
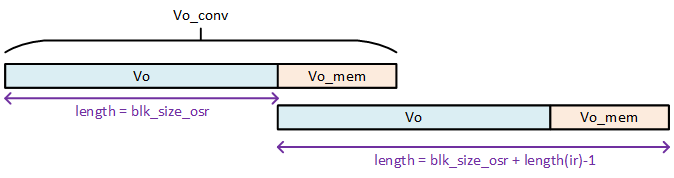
Vo_conv::Vector = zeros(param.blk_size_osr+lastindex(ir)-1) 
Vo = @views Vo_conv[1:param.blk_size_osr] 
Vo_mem = @views Vo_conv[param.blk_size_osr+1:end]

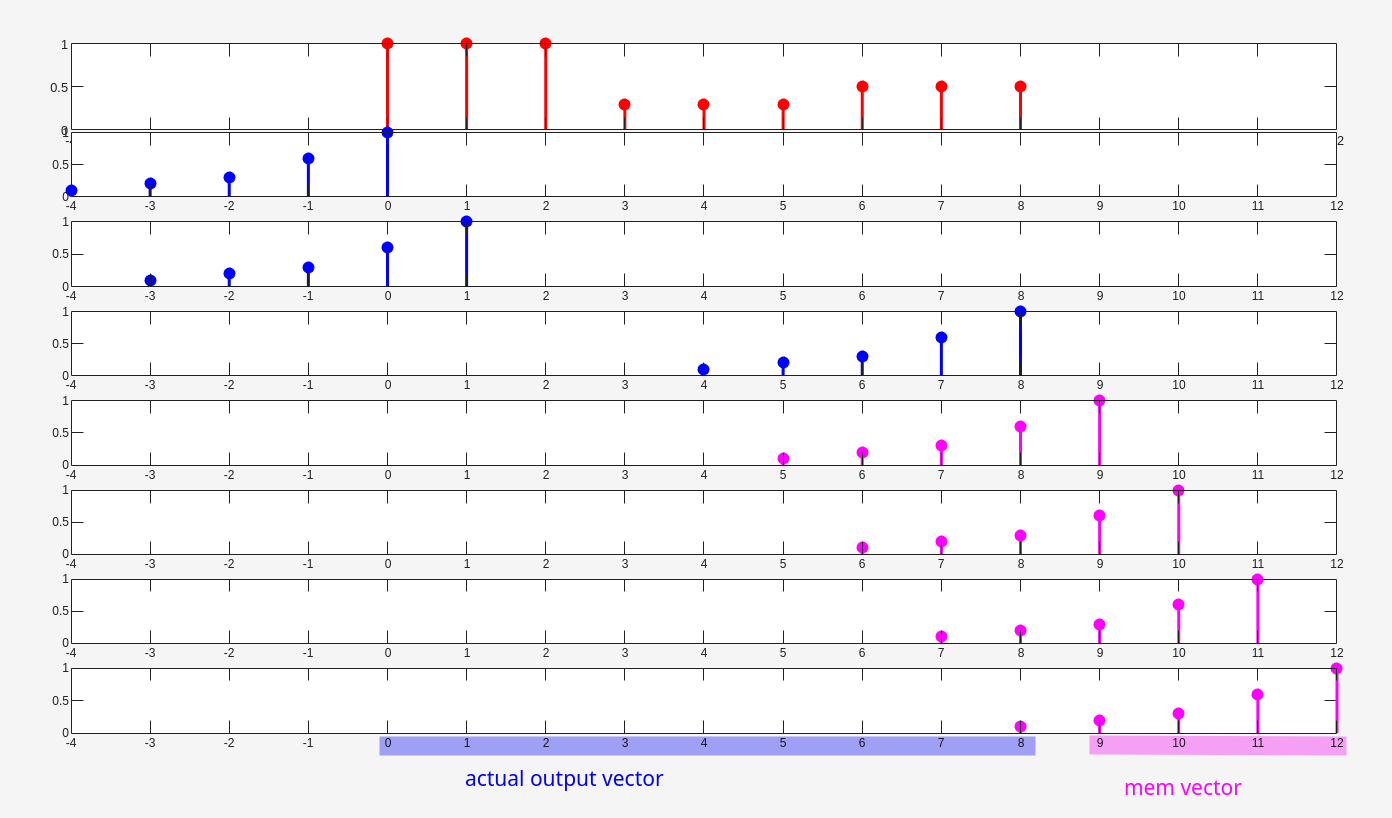
image-20251216230945058

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
si = [1,0.3,0.5];
vi = kron(si, ones(1,3));
xi = 0:1:(length(vi)-1);


subplot(6,1,1)
stem(xi, vi, "filled", 'r', LineWidth=2); xlim([-4,12]); xticks(-4:1:12)

ir = [0.1, 0.2, 0.3, 0.6, 1];
xir = -length(ir)+1:1:0;

subplot(8,1,2)
stem(xir, ir, "filled", 'b', LineWidth=2); xlim([-4,12]); xticks(-4:1:12)

subplot(8,1,3)
stem(xir+1, ir, "filled", 'b', LineWidth=2); xlim([-4,12]); xticks(-4:1:12)

subplot(8,1,4)
stem(xir+8, ir, "filled", 'b', LineWidth=2); xlim([-4,12]); xticks(-4:1:12)

subplot(8,1,5)
stem(xir+9, ir, "filled", 'm', LineWidth=2); xlim([-4,12]); xticks(-4:1:12)

subplot(8,1,6)
stem(xir+10, ir, "filled", 'm', LineWidth=2); xlim([-4,12]); xticks(-4:1:12)

subplot(8,1,7)
stem(xir+11, ir, "filled", 'm', LineWidth=2); xlim([-4,12]); xticks(-4:1:12)

subplot(8,1,8)
stem(xir+12, ir, "filled", 'm', LineWidth=2); xlim([-4,12]); xticks(-4:1:12)

eye diagram based on heatmap

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function w_gen_eye_simple_test(input,x_npts_ui, x_npts, y_range, y_npts; osr, x_ofst=0)
    heatmap = zeros(x_npts, y_npts)

    input_x = 0:1/osr:(lastindex(input)-1)/osr
    itp_resample = linear_interpolation(input_x, input) # interpolation object
    idx_itp = 0:1/x_npts_ui:input_x[end]
    input_itp = itp_resample.(idx_itp)

    for n = 1:x_npts
        heatmap[n,:] = u_hist(input_itp[n:x_npts:end], -y_range/2, y_range/2, y_npts)
    end
   
    return circshift(heatmap, (Int(x_ofst), 0))
end

Julia's interpolation return a function object that can operate on any values you throw at it

eyebin.drawio

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
function u_hist(samples, minval, maxval, nbin)
    weights = zeros(Float64, nbin)
    bin_size = (maxval-minval)/nbin

    for s in samples
        idx = Int(floor((s-minval)/bin_size))+1
        idx = idx < 1 ? 1 : idx > nbin ? nbin : idx
        weights[idx] += 1.0
    end
    return weights
end


feye = Figure()
heatmap!(Axis(feye[1,1]), x_grid, y_grid, eye_tx, 
            colormap=:turbo, #try :inferno, :hot, :viridis
        )
feye

FIR filter typically is much shorter (<10 taps) than the symbol vector, using FFT convolution might be an overkill. For optimization, a simple shift-and-add filter function can be written

image-20260118013730655

1
2
3
4
5
6
7
8
9
10
11
12
13
function u_filt(So_conv, input, fir; Si_mem=Float64[])
    sconv = zeros(length(input) + length(fir) - 1)

    s_in = lastindex(input)
    
    for n=eachindex(fir)
        sconv[n:s_in+n-1] .+= fir[n] .* input
    end

    sconv[eachindex(Si_mem)] .+= Si_mem

    return sconv
end

model jitter with fixed simulation time step

warp or remap a "jittery time grid" onto our "uniform time grid"

1
2
3
4
5
6
7
8
prev_nui = 4
Vext::Vector = zeros(prev_nui*param.osr+param.blk_size_osr)
V_prev_nui = @views Vext[end-prev_nui*param.osr+1:end]  # prev_nui*osr
tt_Vext::Vector = zeros(prev_nui*param.osr+param.blk_size_osr)
Δtt_ext = zeros(param.blk_size+prev_nui+1)  # blk_size + prev_nui + 1
Δtt = zeros(param.blk_size)
Δtt_prev_nui = @views Δtt_ext[end-prev_nui:end]  # prev_nui +  1
tt_uniform::Vector = (0:param.blk_size_osr-1) .+ prev_nui/2*param.osr

Δtt* vectors store the jitter information at each edge location

tt_Vext vector is the jittered time grid vector

tt_uniform is the convience vector to remap the jittered waveform back to our simulation grid

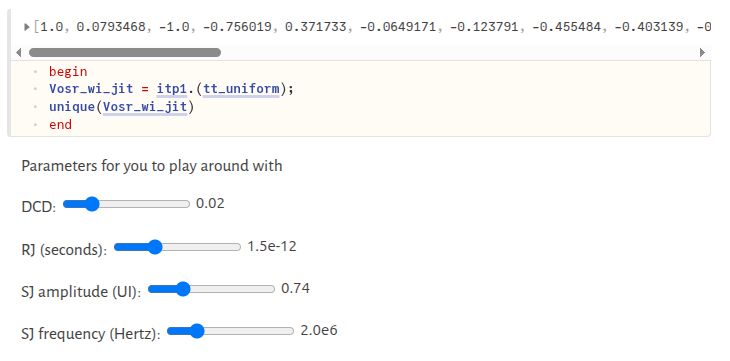
using intermediate voltages embed jitter information at fractional time steps

image-20260208091652420

1
2
drv.Δtt_ext[eachindex(drv.Δtt_prev_nui)] .= drv.Δtt_prev_nui  # 1
drv.Δtt_ext[lastindex(drv.Δtt_prev_nui)+1:end] .= Δtt  # 2

deltatt.drawio

1
2
drv.Vext[eachindex(drv.V_prev_nui)] .= drv.V_prev_nui  # 1
drv.Vext[lastindex(drv.V_prev_nui)+1:end] .= Vosr  # 2

vext.drawio

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function drv_jitter_tvec!(tt_Vext, Δtt_ext, osr)
    for n = 1:lastindex(Δtt_ext)-1
        tt_Vext[(n-1)*osr+1:n*osr] .= LinRange((n-1)*osr+Δtt_ext[n], n*osr+Δtt_ext[n+1], osr+1)[1:end-1]
    end

    return nothing
end

drv_jitter_tvec!(drv.tt_Vext, drv.Δtt_ext, param.osr);

itp = linear_interpolation(drv.tt_Vext, drv.Vext); #itp is a function object

#note here tt_uniform is shifted by prev_nui/2 to give wiggle room for sampling "before" and "after" the current block. This is necessary for sinusoidal jitter
tt_uniform = (0:param.blk_size_osr-1) .+ drv.prev_nui/2*param.osr;

#To interpolate, use the itp object like a function and broadcast to a vector
Vosr_jittered = itp.(tt_uniform); 

# `interp_linear_extrap = linear_interpolation(xs, A, extrapolation_bc=Line())` create #linear interpolation object **with extrapolation**

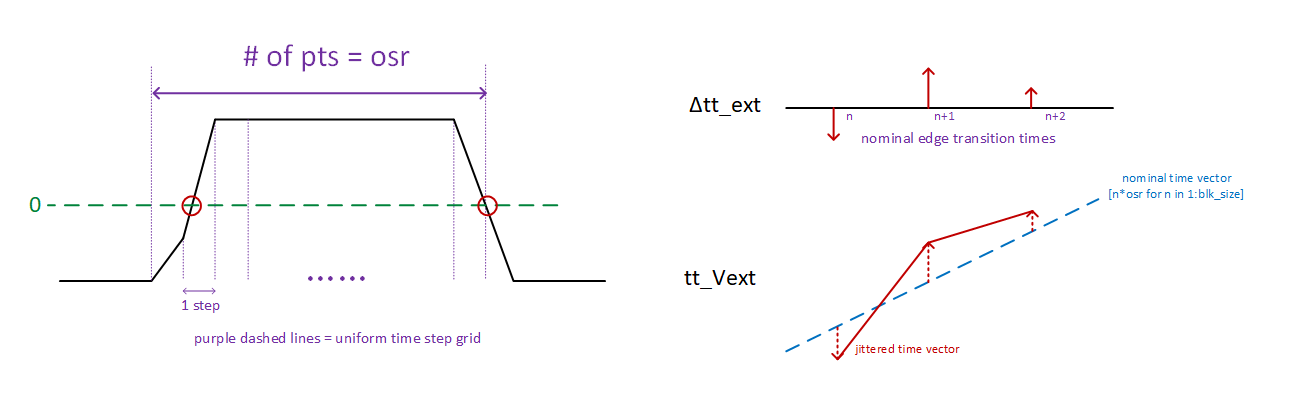
image-20260118180411601

itp = linear_interpolation(drv.tt_Vext, drv.Vext) create linear interpolation object without extrapolation

extrapolation shall not be used to avoid introducing any error

  • prev_nui denotes the number of previous symbols to be stitched to the current block's signal to prevent overflow/underflow when jitter is introduced

  • tt_uniform is shifted by prev_nui/2 to give wiggle room for sampling "before" and "after" the current block. This is necessary for sinusoidal jitter

itp.drawio

a specialized interpolation function to optimize for performance, which support interpolation only

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function drv_interp_jitter!(vo, tt_jitter, vi, tt_uniform)
    last_idx = 1
    for n = eachindex(tt_uniform)
        t = tt_uniform[n]
        for m = last_idx:lastindex(tt_jitter)-1
            if (t >= tt_jitter[m]) && (t < tt_jitter[m+1])
                k = (vi[m+1]-vi[m])/(tt_jitter[m+1]-tt_jitter[m])
                vo[n] = vi[m] + k*(t-tt_jitter[m])
                last_idx = m
                break
            end
        end
    end

    return nothing
end
1
2
3
4
5
drv.Δtt_ext[eachindex(drv.Δtt_prev_nui)] .= drv.Δtt_prev_nui
drv.Δtt_ext[lastindex(drv.Δtt_prev_nui)+1:end] .= Δtt

drv.Vext[eachindex(drv.V_prev_nui)] .= drv.V_prev_nui
drv.Vext[lastindex(drv.V_prev_nui)+1:end] .= Vosr

tt_uniform.drawio

channel

1
2
3
4
5
noise_Z::Float64 = 50  # termination impedance with thermal noise
noise_dbm_hz::Float64 = -174
noise_rms::Float64 = sqrt(0.5/param.dt*10^((noise_dbm_hz-30.0)/10)*noise_Z)

ch.Vch .+= noise_rms .* randn(blk_size_osr)

\[ P_\text{n,dBm/Hz} = 10\times\log_{10} (k_B T / 10^{-3}) = 10\times\log_{10} (k_B T) + 30=-174 \]

Then, \(k_B T = 10^{\frac{-174 - 30}{10}}\)

we have

\[ \sigma_n^2 = 4\cdot k_B T \cdot R \cdot \frac{f_s}{2} = k_B T \cdot R \cdot 2f_s= \frac{\color{red}{2}}{T_s} \cdot 10^{\frac{-174 - 30}{10}} \cdot R \]

noise_rms::Float64 = sqrt(2/param.dt*10^((noise_dbm_hz-30.0)/10) rather than sqrt(0.5/param.dt*10^((noise_dbm_hz-30.0)/10)

run simulation by recursion

1
2
3
4
5
6
function run_blk_iter(trx, idx, n_tot_blk, blk_func::Function)
    if idx < n_tot_blk
        blk_func(trx, idx+1)
        run_blk_iter(trx, idx+1, n_tot_blk, blk_func)
    end
end

Sam Palermo's

continuous time filter (channel, ctle); impulse response

digital filter (FFE, DFE): repmat by samples per UI

Sam Palermo. ECEN 720: High-Speed Links Circuits and Systems [https://people.engr.tamu.edu/spalermo/ecen720.html]

repmat

1
2
3
4
5
6
7
>> repmat([1,2,3], 3, 1)

ans =

     1     2     3
     1     2     3
     1     2     3
1
2
3
4
5
>> reshape(repmat([1,2,3], 3, 1), 1, 3*3)

ans =

     1     1     1     2     2     2     3     3     3

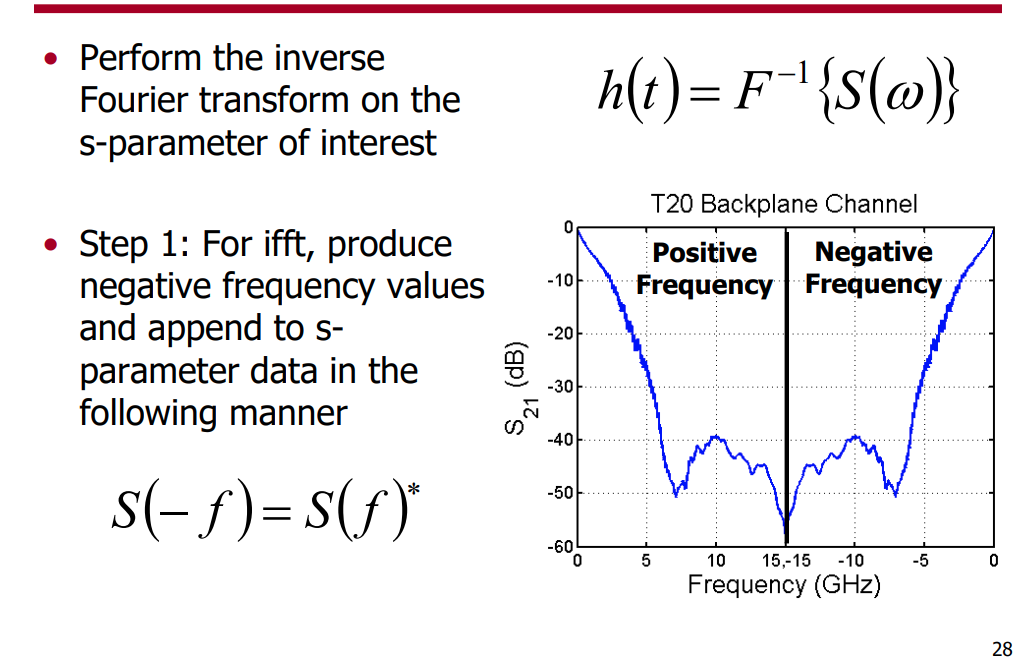
Generating an Impulse Response from S-Parameters

ECEN720: High-Speed Links Circuits and Systems Spring 2025 [https://people.engr.tamu.edu/spalermo/ecen689/lecture3_ee720_tdr_spar.pdf]

image-20251219003532513

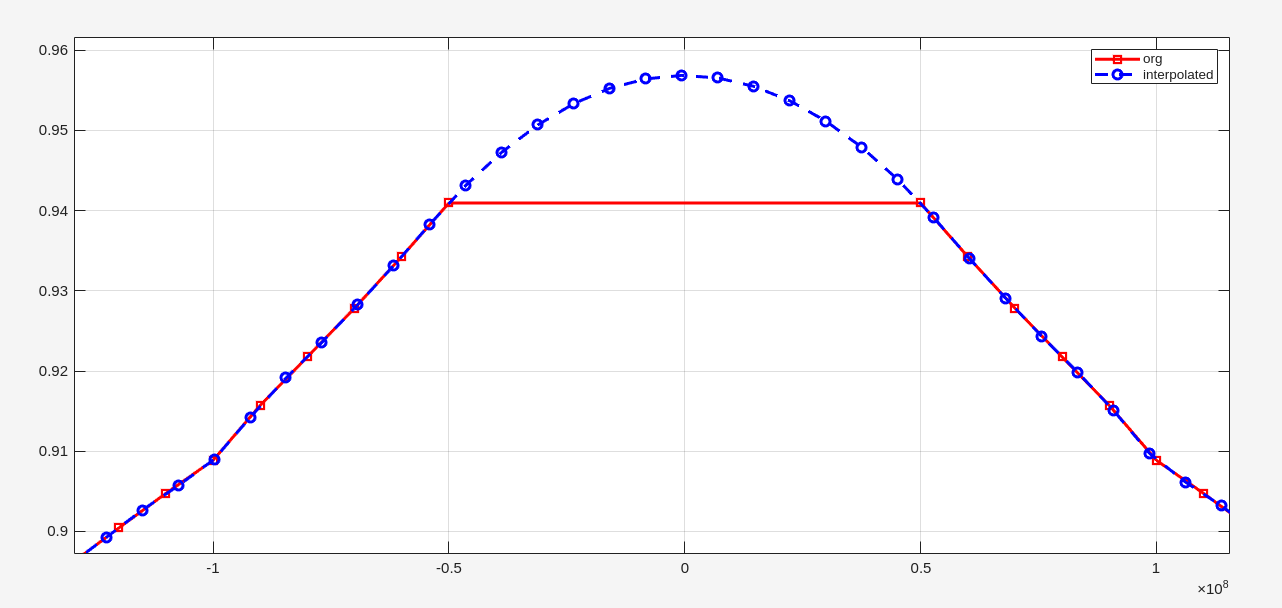
spline: Cubic spline data interpolation

image-20251220171206092

1
2
3
4
5
6
Hm_ds_interp=spline(fds_m,Hm_ds,f_ds_interp); % Interpolate for FFT point number
figure(Name='spline function')
plot(fds_m, Hm_ds, '-rs', LineWidth=2)
hold on
plot(f_ds_interp, Hm_ds_interp, '--bo', LineWidth=2)
legend('org', 'interpolated'); grid on

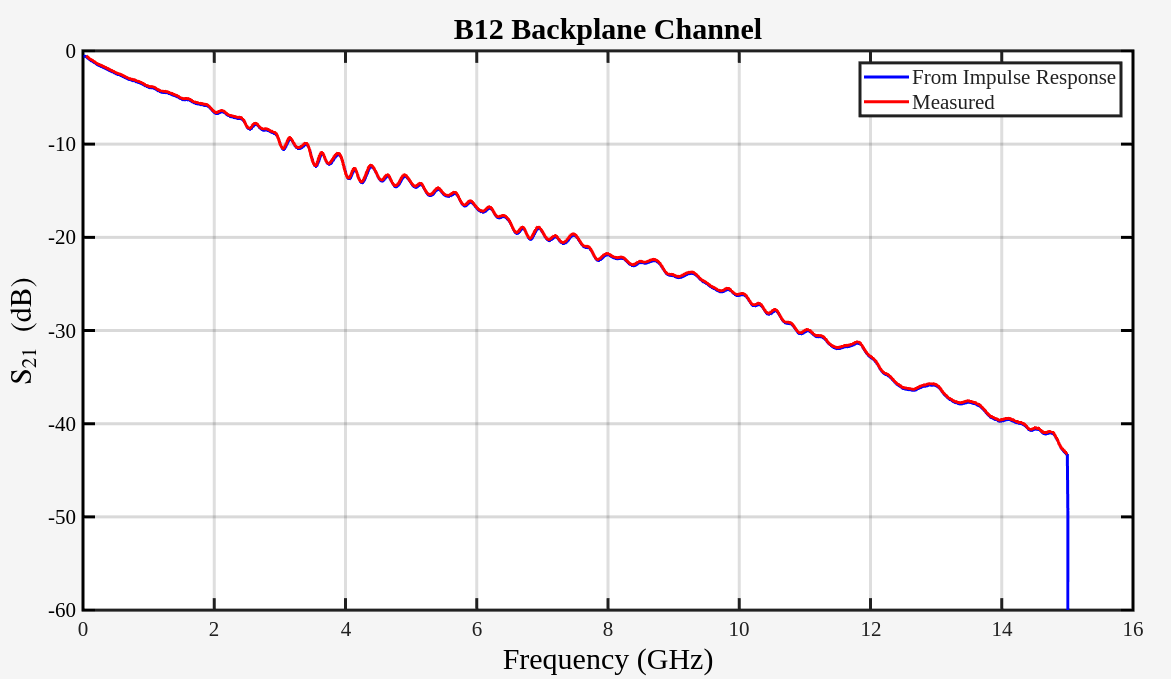
impulse response from ifft of interpolated frequency response

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
% https://people.engr.tamu.edu/spalermo/ecen689/xfr_fn_to_imp.m

% Generate Random Data
nt=1e3;         %number of bits
m=rand(1,nt+1);     %random numbers between 1 and zero, will be quantized later
m=-1*sign(m-0.5).^2+sign(m-0.5)+1;


% TX FIR Equalization Taps
eq_taps=[1];
m_fir=filter(eq_taps,1,m);


m_dr=reshape(repmat(m_fir,bit_period,1),1,bit_period*size(m_fir,2));

data_channel=0.5*conv(sig_ir(:,1),m_dr(1:nt*bit_period));

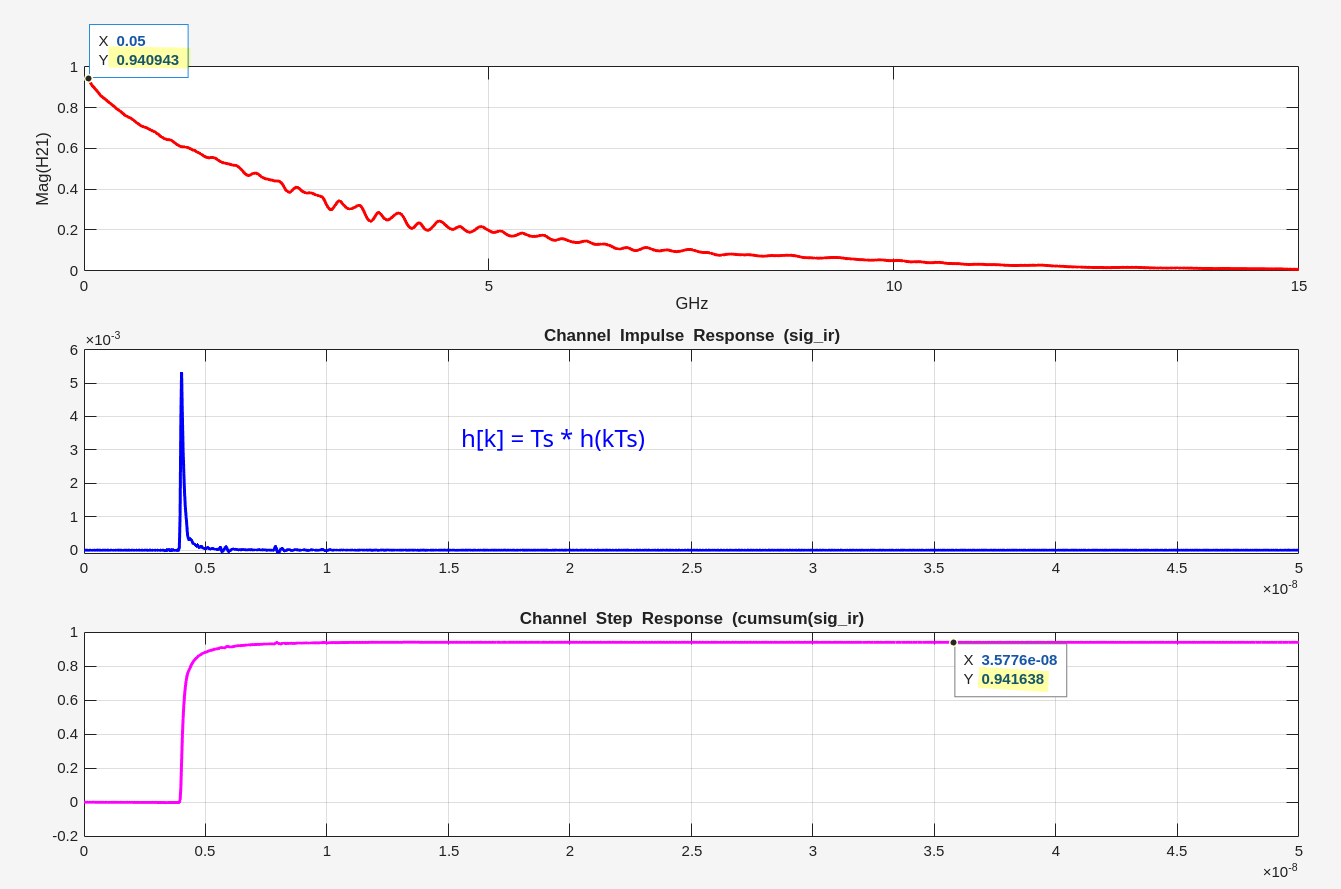
image-20251219010707990

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
subplot(3,1,1)

FileName = './peters_01_0605_B12_thru.s4p';
SingleEndedData = read(rfdata.data, FileName);
Freq = SingleEndedData.Freq;
DifferentialSparams = s2sdd(SingleEndedData.S_Parameters);
rfdata.network('Data', DifferentialSparams, 'Freq', Freq);
H21 = DifferentialSparams(2,1,:);

plot(Freq'*1e-9, abs(H21(:)),'-r', LineWidth=2);
xlabel('GHz'); ylabel('Mag(H21)'); grid on;


subplot(3,1,2)
load './ir_B12.mat';
tsample=1e-12;  % Impluse response has 1ps time step
sample_num=size(ir,1);  
sig_ir=ir(:,1); 

time=(1:size(sig_ir,1))*1e-12;

plot(time, sig_ir, '-b', LineWidth=2);
title('Channel Impulse Response (sig_ir)'); grid on;


subplot(3,1,3)
step_resp = cumsum(sig_ir); % Ts factor embedded in sig_ir
plot(time, step_resp, '-m', LineWidth=2);
title('Channel Step Response (cumsum(sig_ir)'); grid on;
1
2
plot(ch1_freqs,20*log10(abs(ch1)),'-b',Freq'*1e-9,20*log10(abs(H21)),'-r');
legend('From Impulse Response','Measured');

image-20251220171711739

plot eye diagram

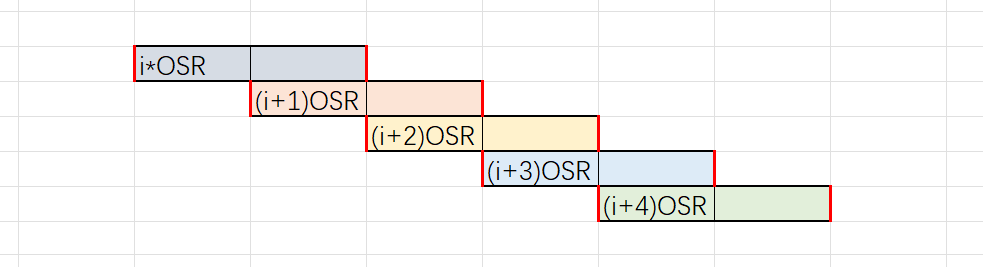
image-20251220001630173

1
2
3
4
5
6
7
8
9
10
11
12
13
14
% https://people.engr.tamu.edu/spalermo/ecen689/channel_data.m

data_channel=0.5*conv(sig_ir(:,1),m_dr(1:nt*bit_period));

j=1;
offset=144;

for ( i=55:floor(size(data_channel,2) / bit_period)-500)
    eye_data(:,j) = 2*data_channel(floor((bit_period*(i-1)))+offset: floor((bit_period*(i+1)))+offset);
    j=j+1;
end

time=0:2*bit_period;
plot(time,eye_data);

If your 2D array represents multiple data series (e.g., each column is a separate line series sharing the same x-axis values), the plot() function is the most straightforward method.

[https://people.engr.tamu.edu/spalermo/ecen689/lecture4_ee720_channel_pulse_model.pdf]

image-20251220204006939

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
% https://people.engr.tamu.edu/spalermo/ecen689/tx_eq.m

precursor_samples=10;
pulse_response=conv(ir_process,ones(1,bit_period));
[max_pulse_value,max_pulse_time]=max(pulse_response);
sample_times=[max_pulse_time-1*precursor_samples*bit_period:bit_period:max_pulse_time+30*bit_period];
sample_values=pulse_response(sample_times);

% Construct H matrix
H(:,1)=sample_values';
H(size(sample_values,1)+1:size(sample_values,1)+eq_tap_number-1,1)=0;
for i=2:eq_tap_number
    H(1:i-1,i)=0;
    H(i:size(sample_values,1)+i-1,i)=sample_values';
    H(size(sample_values,1)+i:size(sample_values,1)+eq_tap_number-1,1)=0;
end;


% Construct Y matrix
Ydes(1:precursor_samples+precursor_number,1)=0;
Ydes(precursor_samples+precursor_number+1,1)=1;
Ydes(precursor_samples+precursor_number+2:size(H,1),1)=0;

W=(H'*H)^(-1)*H'*Ydes

Itot=1;
taps=Itot*W/sum(abs(W));

TX FIR Tap Resolution

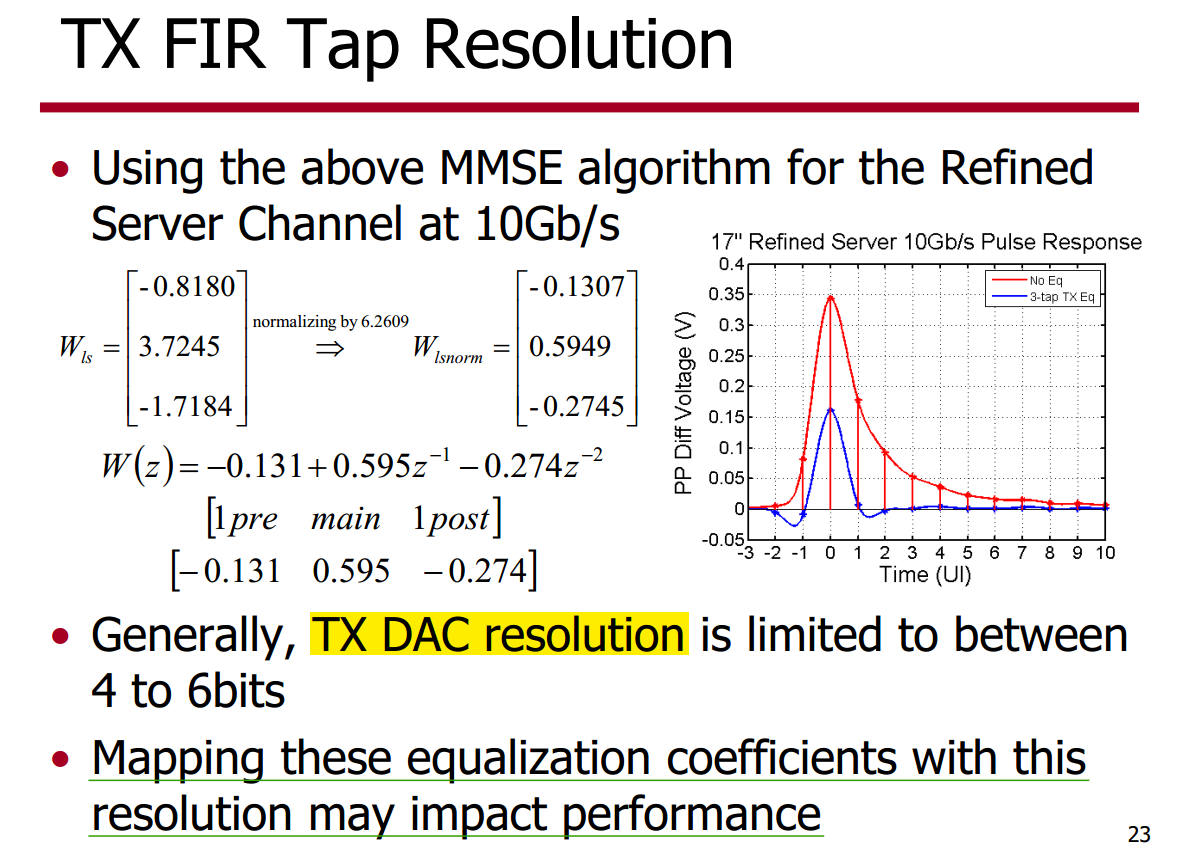
image-20251220205819019

1
2
3
4
5
6
7
8
9
10
% https://people.engr.tamu.edu/spalermo/ecen689/tx_eq.m

taps_abs=abs(taps);
taps_sign=sign(taps);

partition=[1/(2*(2^num_bits-1)):1/(2^num_bits-1):1-1/(2*(2^num_bits-1))];
codebook=[0:1/(2^num_bits-1):1];
[index,abs_taps_quan]=quantiz(abs(taps),partition,codebook);
taps_quan=taps_sign'.*abs_taps_quan;
taps_quan(precursor_number+1)=sign(taps_quan(precursor_number+1))*(1-(sum(abs(taps_quan))-abs(taps_quan(precursor_number+1))));

CTLE modeling by impulse response

Given two impulse response \(h_0(t)\), \(h_1(t)\) and \(h_0(t)*h_1(t) = h_{tot}(t)\), we have \[ T_s h_0(kT_s) * T_sh_1(kT_s) = T_s h_{tot}(kT_s) \]

To use the filter function with the b coefficients from an FIR filter, use y = filter(b,1,x)

CTLE response from frequency response using ifft

data-driven frequency table

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
% https://people.engr.tamu.edu/spalermo/ecen689/gen_ctle.m

Hk_ext = [Hk conj(Hk(end-1:-1:2))] ;

hn_ext_ifft = real(ifft(Hk_ext, 'symmetric'));
hn_ext_ifft(1) = (2 * hn_ext_ifft(1));
%interpolate ifft
N = length(ctle.f_arr);
Ts = (1 / (2*fmax));
t_arr = ((0 : (N-1)) * Ts); Tmax = t_arr(end); %10e-9; 
treqd = (0 : time_step : Tmax);
%interpolate step response instead of impulse response
sr_ifft = cumsum(hn_ext_ifft(1:length(t_arr))); sr_ifft_t = t_arr;
sr_interp = interp1(sr_ifft_t, sr_ifft, treqd, 'spline');
ir_interp = diff(sr_interp);
ir_ctle = ir_interp; clear ir_interp;

%scale by gain adjustment factor
ir_ctle = (ir_ctle * ctle.gain_adjust_fac);
ir_out = filter(ir_ctle, 1, ir_in);

CTLE response from pole/zero using tf & impulse

1
2
3
H21 = tf();
tsamples = 0:Ts:nUI
ir = Ts*impulse(H21, tsamples)  % scaling by Ts is necessary

CTLE response from pole/zero using bilinear discretization

analytical pole/zero transfer function, [Google AI Mode]

image-20251221091355318

image-20251221093230806

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
% https://people.engr.tamu.edu/spalermo/ecen689/gen_ctle.m

A_dc=max(A_dc,1e-3);
zeq=max(zeq,1);
peq=max(peq,1);

gbw_rad=gbw*2*pi;
zeq_rad=zeq*2*pi;
peq_rad=peq*2*pi;

ppar=(gbw_rad*zeq_rad)/(A_dc*peq_rad);

a_tf=A_dc*peq_rad*ppar;
b_tf=A_dc*peq_rad*ppar*zeq_rad;
c_tf=zeq_rad;
d_tf=(peq_rad+ppar)*zeq_rad;
e_tf=peq_rad*ppar*zeq_rad;


B_filt=[2*a_tf/time_step+b_tf;
    2*b_tf;
    b_tf-2*a_tf/time_step]';

A_filt=[4*c_tf/time_step^2+2*d_tf/time_step+e_tf;
    2*e_tf-8*c_tf/time_step^2;
    4*c_tf/time_step^2-2*d_tf/time_step+e_tf]';

B_filt=B_filt/A_filt(1);
A_filt=A_filt/A_filt(1);

ir_out=filter(B_filt,A_filt,ir_in);

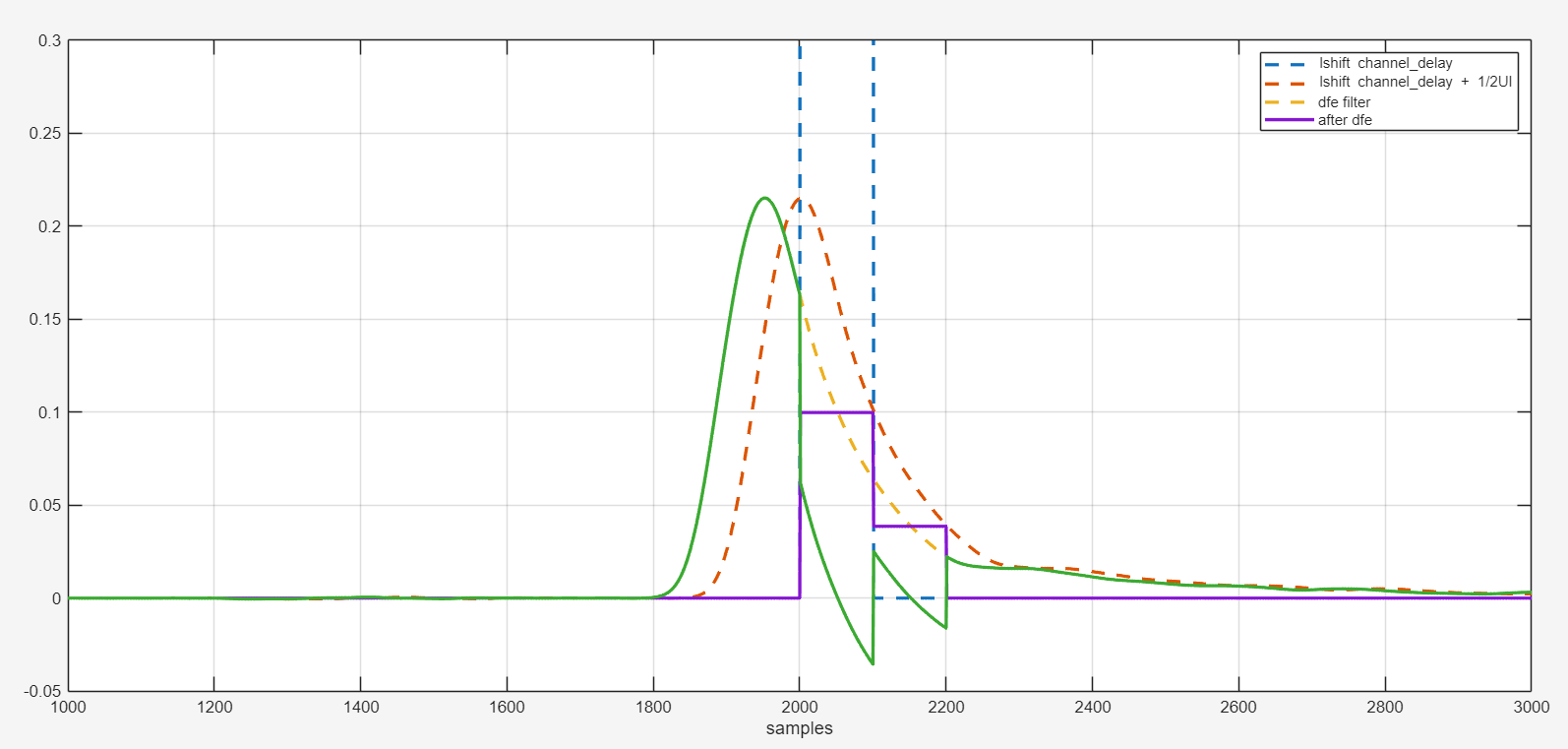
rx dfe

pseudo linear equalizer

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
% https://people.engr.tamu.edu/spalermo/ecen689/channel_data_pulse_pda_dfe.m

% Take 10 pre-cursor, cursor, and 90 post-cursor samples
sample_offset=opt_sample*bit_period;
for i=1:101
sample_points(i)=max_data_ch_idx+sample_offset+(i-11)*bit_period;
end
sample_values=data_channel(sample_points);
sample_points=(sample_points-max_data_ch_idx)./bit_period;

channel_delay=max_data_ch_idx-(20*bit_period+1);  % !! 20*bit_period = 2000

% Include DFE Equalization
dfe_tap_num=2;
dfe_taps(1:dfe_tap_num)=sample_values(12:12+dfe_tap_num-1);  % h1, h2...

% Note this isn't a strtict DFE implementation - as I am not making a
% decision on the incoming data.  Rather, I am just using the known data
% that I transmitted, delay matching this with the channel data, and using 
% it to subtract the ISI after weighting with the tap values.  But, I think 
% it is good enough for these simulations.
m_dfe=filter(dfe_taps,1,m);
m_dfe_dr=reshape(repmat(m_dfe,bit_period,1),1,bit_period*size(m_dfe,2));

data_channel=data_channel';
dfe_fb_offset=floor(bit_period/2); % Point at which the DFE taps are subtracted - can be anything from 0 to UI-1*time_step
data_channel_dfe=data_channel(channel_delay+dfe_fb_offset:channel_delay+dfe_fb_offset+size(m_dfe_dr,2)-1)-m_dfe_dr;

image-20251221152624033

1
2
3
4
5
6
7
plot(m_dr, '--', LineWidth=2); hold on
plot(data_channel(channel_delay:end), '--', LineWidth=2)
hold on
plot(data_channel(channel_delay+dfe_fb_offset:channel_delay+dfe_fb_offset+size(m_dfe_dr,2)-1), '--', LineWidth=2)
plot(m_dfe_dr, LineWidth=2); plot(data_channel_dfe, LineWidth=2)
xlim([1000, 3000]); ylim([-0.05, 0.3]); xlabel('samples'); grid on
legend('lshift channel\_delay', 'lshift channel\_delay + 1/2UI', 'dfe filter', 'after dfe')

DaVE

Byongchan Lim. DaVE — tools regarding on analog modeling, validation, and generation, [https://github.com/StanfordVLSI/DaVE]

TODO 📅

Statistical Eye

Sanders, Anthony, Michael Resso and John D'Ambrosia. “Channel Compliance Testing Utilizing Novel Statistical Eye Methodology.” (2004) [https://people.engr.tamu.edu/spalermo/ecen689/stateye_theory_sanders_designcon_2004.pdf]

X. Chu, W. Guo, J. Wang, F. Wu, Y. Luo and Y. Li, "Fast and Accurate Estimation of Statistical Eye Diagram for Nonlinear High-Speed Links," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 29, no. 7, pp. 1370-1378, July 2021 [https://sci-hub.se/10.1109/TVLSI.2021.3082208]

HSPICE® User Guide: Signal Integrity Modeling and Analysis, Version Q-2020.03, March 2020

IA Title: Common Electrical I/O (CEI) - Electrical and Jitter Interoperability agreements for 6G+ bps, 11G+ bps, 25G+ bps I/O and 56G+ bps IA # OIF-CEI-04.0 December 29, 2017 [pdf]

J. Park and D. Kim, "Statistical Eye Diagrams for High-Speed Interconnects of Packages: A Review," in IEEE Access, vol. 12, pp. 22880-22891, 2024 [pdf]

StatOpt

Savo Bajic, ECE1392, Integrated Circuits for Digital Communications: StatOpt in Python [https://savobajic.ca/projects/academic/statopt] [https://www.eecg.utoronto.ca/~ali/statopt/main.html]

TODO 📅

pystateye

Chris Li. pystateye - A Python Implementation of Statistical Eye Analysis and Visualization [https://github.com/ChrisZonghaoLi/pystateye]

TODO 📅

other framework

pyBERT

David Banas. pyBERT: Free software for signal-integrity analysis [https://github.com/capn-freako/PyBERT], [intro]

—. Free yourself from IBIS-AMI models with PyBERT [https://www.edn.com/free-yourself-from-ibis-ami-models-with-pybert/]

TODO 📅

PyChOpMarg

David Banas. Python implementation of COM, as per IEEE 802.3-22 Annex 93A. [https://github.com/capn-freako/PyChOpMarg]

CC Chen. Why Channel Operating Margin? [https://youtu.be/mrXur-WbrR8]

TODO 📅

mmse_dfe

Chris Li, jointly optimizing feed-forward equalizer (FFE) and decision-feedback equalizer (DFE) tap weights [https://github.com/ChrisZonghaoLi/mmse_dfe]

John M. Cioffi, Chapter 3 - Equalization [https://cioffi-group.stanford.edu/doc/book/chap3.pdf]

TODO 📅

Helper Functions

int2bits

[https://github.com/kevjzheng/JLSD/blob/4ac92476b67ce78e01820502eb3b4afb6d31bcd7/src/blks/BlkBIST.jl#L126-L128]

1
2
3
function int2bits(num, nbit)
	return [Bool((num>>k)%2) for k in nbit-1:-1:0]
end

PRBS Generator

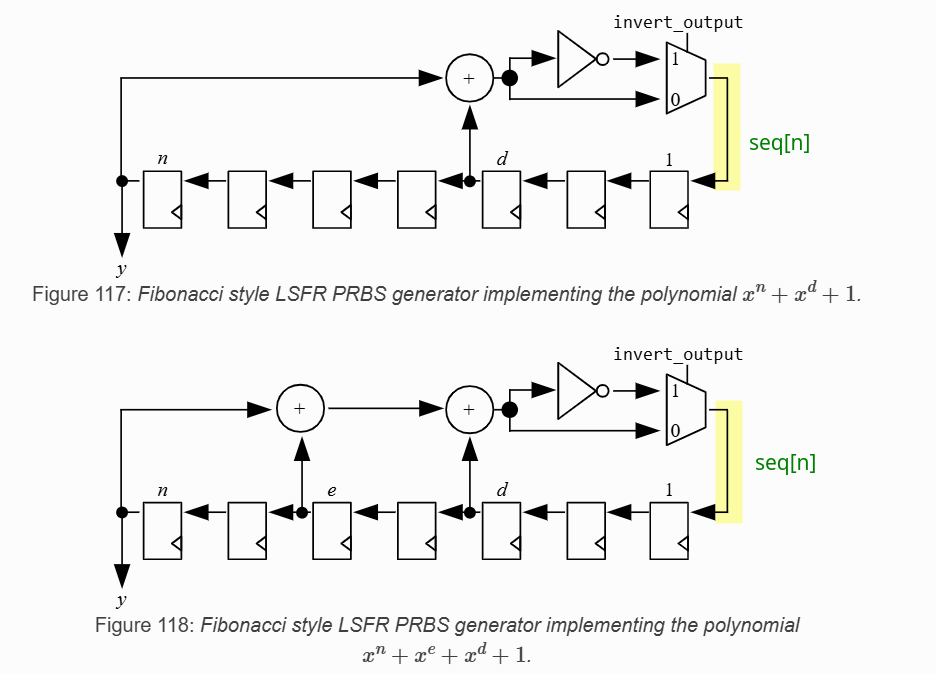
image-20251008232419923

[https://opencpi.gitlab.io/releases/latest/rst/comp_sdr/components/generator/prbs_generator_b.comp/prbs_generator_b-index.html]

1
2
3
4
5
6
7
8
9
10
11
12
13
# Julia

function bist_prbs_gen(;poly, inv, Nsym, seed)
    seq = Vector{Bool}(undef,Nsym)
    for n = 1:Nsym
        seq[n] = inv
        for p in poly
            seq[n] ⊻= seed[p]
        end
        seed .= [seq[n]; seed[1:end-1]]
    end
    return seq, seed
end
1
2
3
4
5
6
7
8
9
10
11
12
%% Matlab

function [seq, seed] = bist_prbs_gen(poly,inv, Nsym, seed)
    seq = zeros(1,Nsym);
    for n = 1:Nsym
        seq(n) = inv;
        for p = poly
            seq(n) = xor(seq(n), seed(p));
        end
       seed = [seq(n), seed(1:end-1)];
    end
end

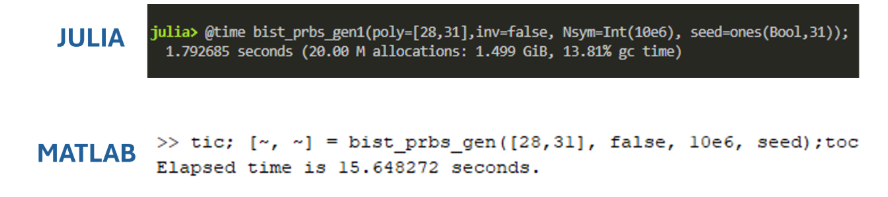
image-20251003110528405

[https://github.com/kevjzheng/JLSD/blob/main/Pluto%20Notebooks/pdf/JLSD_pt1_background.pdf]

PRBS Checker

[https://github.com/kevjzheng/JLSD/blob/4ac92476b67ce78e01820502eb3b4afb6d31bcd7/Pluto%20Notebooks/jl/JLSD_pt2_framework.jl#L198-L235]

previous bit determine current bit

bert.drawio

  1. current LSFR generate btst
  2. compare bst with current brcv
  3. push current brcv into LSFR

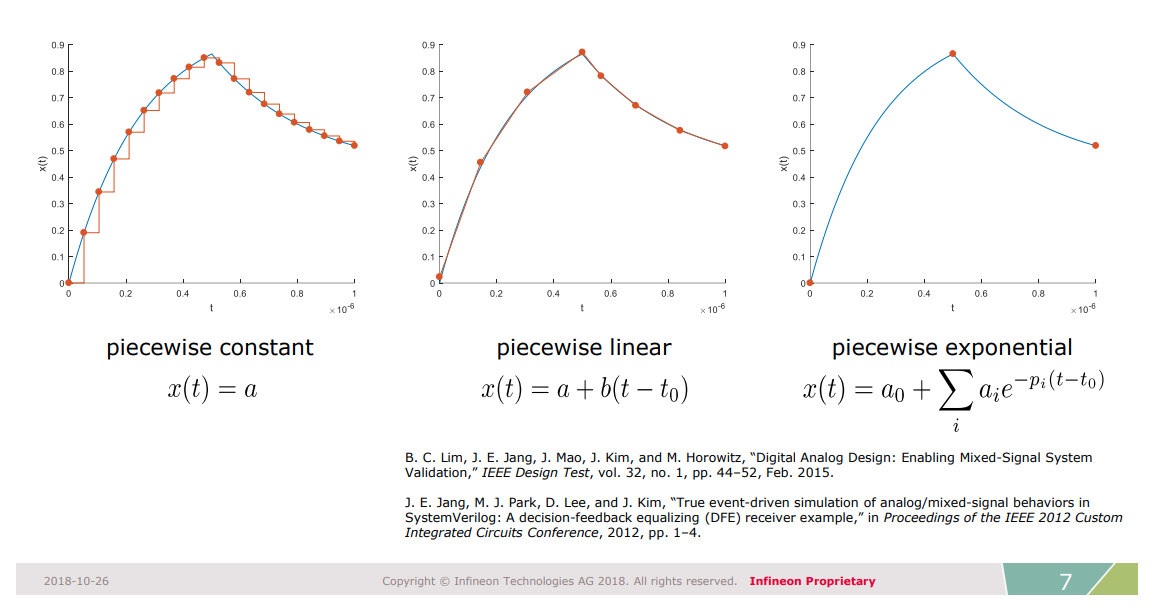
Analog Signals Representation

Ben Yochret Sabrine, 2020, "BEHAVIORAL MODELING WITH SYSTEMVERILOG FOR MIXED-SIGNAL VALIDATION" [https://di.uqo.ca/id/eprint/1224/1/Ben-Yochret_Sabrine_2020_memoire.pdf]

image-20250913234701819

image-20250914115332274

Reference

MATLAB® and Simulink® RF and Mixed Signal [https://www.mathworks.com/help/overview/rf-and-mixed-signal.html]

Lim, Byong Chan, M. Horowitz, "Error Control and Limit Cycle Elimination in Event-Driven Piecewise Linear Analog Functional Models," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 63, no. 1, pp. 23-33, Jan. 2016 [https://sci-hub.se/10.1109/TCSI.2015.2512699]

—, Ph.D. Dissertation 2012. "Model validation of mixed-signal systems" [https://stacks.stanford.edu/file/druid:xq068rv3398/bclim-thesis-submission-augmented.pdf]

—, J. -E. Jang, J. Mao, J. Kim and M. Horowitz, "Digital Analog Design: Enabling Mixed-Signal System Validation," in IEEE Design & Test, vol. 32, no. 1, pp. 44-52, Feb. 2015 [http://iot.stanford.edu/pubs/lim-mixed-design15.pdf]

— , Mao, James & Horowitz, Mark & Jang, Ji-Eun & Kim, Jaeha. (2015). Digital Analog Design: Enabling Mixed-Signal System Validation. Design & Test, IEEE. 32. 44-52. [https://iot.stanford.edu/pubs/lim-mixed-design15.pdf]

S. Liao and M. Horowitz, "A Verilog piecewise-linear analog behavior model for mixed-signal validation," Proceedings of the IEEE 2013 Custom Integrated Circuits Conference, San Jose, CA, USA, 2013 [https://sci-hub.se/10.1109/CICC.2013.6658461]

—, M. Horowitz, "A Verilog Piecewise-Linear Analog Behavior Model for Mixed-Signal Validation," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 61, no. 8, pp. 2229-2235, Aug. 2014 [https://sci-hub.se/10.1109/TCSI.2014.2332265]

—,Ph.D. Dissertation 2012. Verilog Piecewise Linear Behavioral Modeling For Mixed-Signal Validation [https://stacks.stanford.edu/file/druid:pb381vh2919/Thesis_submission-augmented.pdf]

Ji-Eun Jang et al. “True event-driven simulation of analog/mixed-signal behaviors in SystemVerilog: A decision-feedback equalizing (DFE) receiver example”. In: Proceedings of the IEEE 2012 Custom Integrated Circuits Conference. 2012 [https://sci-hub.se/10.1109/CICC.2012.6330558]

—, Si-Jung Yang, and Jaeha Kim. “Event-driven simulation of Volterra series models in SystemVerilog”. In: Proceedings of the IEEE 2013 Custom Integrated Circuits Conference. 2013 [https://sci-hub.se/10.1109/CICC.2013.6658460]

—, Ph.D. Dissertation 2015. Event-Driven Simulation Methodology for Analog/Mixed-Signal Systems [file:///home/anon/Downloads/000000028723.pdf]

"Creating Analog Behavioral Models VERILOG-AMS ANALOG MODELING" [https://www.eecis.udel.edu/~vsaxena/courses/ece614/Handouts/CDN_Creating_Analog_Behavioral_Models.pdf]

Rainer Findenig, Infineon Technologies. "Behavioral Modeling for SoC Simulation Bridging Analog and Firmware Demands" [https://www.coseda-tech.com/files/Files/Dokumente/Behavioral_Modeling_for_SoC_Simulation_COSEDA_UGM_2018.pdf]

CC Chen. Why Efficient SPICE Simulation Techniques for BB CDR Verification? [https://youtu.be/Z54MV9nuGUI]

T. Wen and T. Kwasniewski, "Phase Noise Simulation and Modeling of ADPLL by SystemVerilog," 2008 IEEE International Behavioral Modeling and Simulation Workshop, San Jose, CA, USA, 2008 [slides, paper]

Jaeha Kim,Scientific Analog. UCIe PHY Modeling and Simulation with XMODEL [pdf]

S. Katare, "Novel Framework for Modelling High Speed Interface Using Python for Architecture Evaluation," 2020 IEEE REGION 10 CONFERENCE (TENCON), Osaka, Japan, 2020 [https://sci-hub.se/10.1109/TENCON50793.2020.9293846]

G. Balamurugan, A. Balankutty and C. -M. Hsu, "56G/112G Link Foundations Standards, Link Budgets & Models," 2019 IEEE Custom Integrated Circuits Conference (CICC), Austin, TX, USA, 2019, pp. 1-95 [https://youtu.be/OABG3u2H2J4] [https://picture.iczhiku.com/resource/ieee/SHKhwYfGotkIymBx.pdf]

Mathuranathan Viswanathan. Digital Modulations using Matlab: Build Simulation Models from Scratch