Pole-Zero Doublet

Posted on 2022-12-14 Edited on 2023-07-10 In analog

Mismatch between the pole and zero frequencies leads to the “doublet problem”. If the pole and the zero do not exactly coincide, we say that they constitute a doublet

Problem 10.19 in Razavi 2nd book

Suppose the open-loop transfer function of a two-stage op amp is expressed as \[ H_{open}(s)=\frac{A_0(1+\frac{s}{\omega_z})}{\left( 1+ \frac{s}{\omega_{p1}}\right)\left( 1+ \frac{s}{\omega_{p2}}\right)} \] Ideally, \(\omega_z=\omega_2\) and the feedback circuit exhibits a first-order behavior, i.e., its step response contains a single time constant and no overshoot.

Then the transfer function of the amplifier in a unity-gain feedback loop is given by \[\begin{align} H_{closed}(s) &=\frac{A_0\left(1+\frac{s}{\omega_z}\right)}{\frac{s^2}{\omega_{p1}\omega_{p2}}+\left( \frac{1}{\omega_{p1}} + \frac{1}{\omega_{p2}}+\frac{A_0}{\omega_{z}}\right)s+A_0+1} \\ &=\frac{\frac{A_0}{A_0+1}(1+\frac{s}{\omega_z})}{\frac{s^2}{\omega_{p1}\omega_{p2}(A_0+1)}+\left( \frac{1}{\omega_{p1}} + \frac{1}{\omega_{p2}}+\frac{A_0}{\omega_{z}}\right)\frac{s}{A_0+1}+1} \end{align}\]

The denominator part of \(H_{closed}(s)\) is \[ D(s) = \frac{s^2}{\omega_{p1}\omega_{p2}}+\left( \frac{1}{\omega_{p1}} + \frac{1}{\omega_{p2}}+\frac{A_0}{\omega_{z}}\right)s+A_0+1 \]

Assuming two poles (\(\omega_{pA} \ll\omega_{pB}\)) of \(H_{closed}(s)\) are widely spaced, \[\begin{align} D(s) &= \left( 1+ \frac{s}{\omega_{pA}}\right)\left( 1+ \frac{s}{\omega_{pB}}\right)\\ &\cong \frac{s^2}{\omega_{pA}\omega_{pB}}+\frac{s}{\omega_{pA}} + 1 \end{align}\]

Thus, the two poles of the closed-loop transfer function of system are \[\begin{align} \omega_{pA} &= \frac{A_0+1}{\frac{1}{\omega_{p1}} + \frac{1}{\omega_{p2}}+\frac{A_0}{\omega_{z}}} \\ &= \frac{(A_0+1)\omega_{p1} \omega_{p2}}{\omega_{p1} + \omega_{p2} + \frac{A_0}{\omega_z}\omega_{p1} \omega_{p2}} \\ \omega_{pB} &= \omega_{p1} + \omega_{p2} + \frac{A_0}{\omega_z}\omega_{p1} \omega_{p2} \end{align}\]

Assuming \(\omega_z \simeq \omega_{p2}\) and \(\omega_{p2}\ll (1+A_0)\omega_{p1}\) \[ \omega_{pA} = \omega_{p2} \] and \[ \omega_{pB} = (1+A_0)\omega_{p1} \] The closed-loop transfer function is \[ H_{closed}(s) = \frac{\frac{A_0}{A_0+1}\left(1+\frac{s}{\omega_z}\right)}{\left(1+\frac{s}{(1+A_0)\omega_{p1}}\right)\left( 1+\frac{s}{\omega_{p2}} \right)} \]

The step response of the closed-loop amplifier

Consider the Laplace transform function of step response, \(X(s)=\frac{1}{s}\) \[ Y(s)=\frac{1}{s}\times H_{closed}(s) \] Thus, the small-signal step response of the closed-loop amplifier is \[ y(t)=\frac{A_0}{A_0+1}\left[1-e^{-(A_0+1)\omega_{p1}t}-\left(1-\frac{\omega_{p2}}{\omega_z}\right)e^{-\omega_{p2}t} \right]u(t) \] Since, \(\omega_{p2}\ll (1+A_0)\omega_{p1}\). Therefore, rewrite the \(y(t)\) \[ y(t)\cong \frac{A_0}{A_0+1}\left[1-\left(1-\frac{\omega_{p2}}{\omega_z}\right)e^{-\omega_{p2}t} \right]u(t) \] The step response contains an exponential term of the form \(\left(1-\frac{\omega_{p2}}{\omega_z}\right)e^{-\omega_{p2}t}\). This is an important result, indicating that if the zero does not exactly cancel the pole, the step response exhibits an exponential with an amplitude proportional to \(\left(1-\frac{\omega_{p2}}{\omega_z}\right)\), which depends on the mismatch between \(\omega_z\) and \(\omega_{p2}\) and a time constant \(\tau\) of \(\frac{1}{\omega_{p2}}\) or \(\frac{1}{\omega_{z}}\)

perfect pole-zero cancellation

\[\begin{align} y(t) &=\frac{A_0}{A_0+1}\left[1-e^{-(A_0+1)\omega_{p1}t}-\left(1-\frac{\omega_{p2}}{\omega_z}\right)e^{-\omega_{p2}t} \right]u(t) \\ &= \frac{A_0}{A_0+1}\left[1-e^{-(A_0+1)\omega_{p1}t}\right]u(t) \end{align}\]

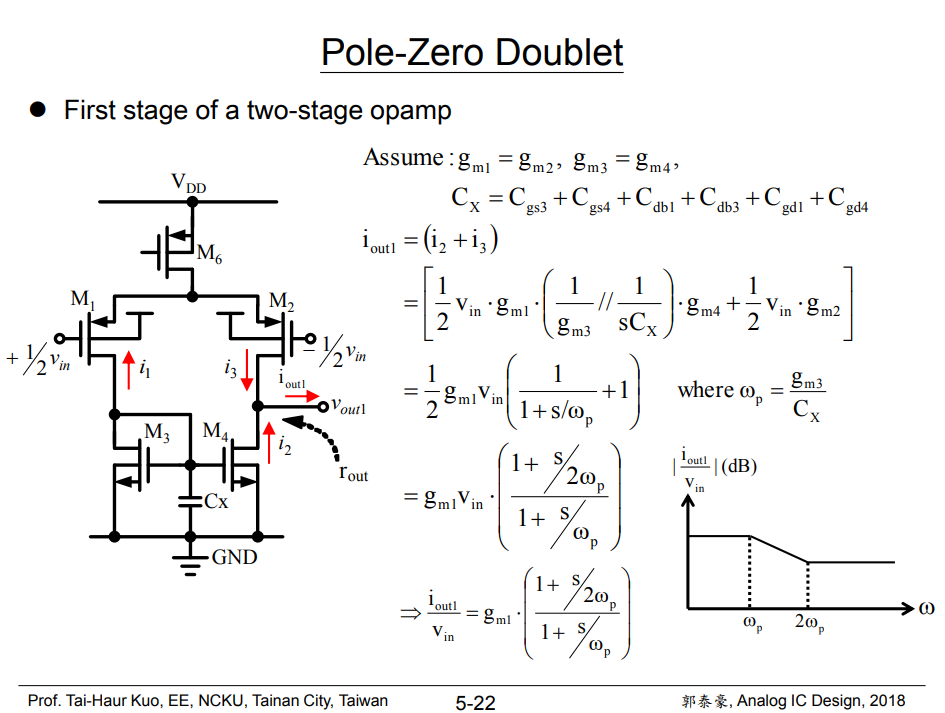
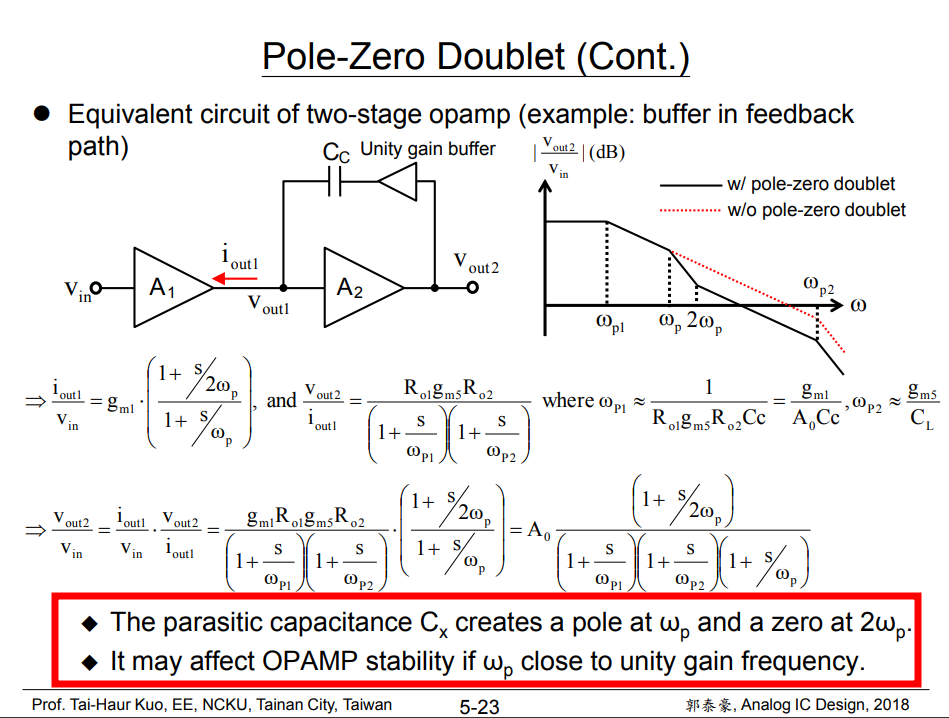
The zero comes from the mirror node

Thanks to unity gain buffer, zero is alleviated for \(C_c\)

reference

Elad Alon, Lecture 10: Settling-Limited Amplifier Design Methodology, EE 240B – Spring 2018, Advanced Analog Integrated Circuits https://inst.eecs.berkeley.edu/~ee240b/sp18/lectures/Lecture10_Settling_Design_2up.pdf

Eric Chang, Prof. Elad Alon EE240B HW3 https://inst.eecs.berkeley.edu/~ee240b/sp18/homeworks/hw3.pdf and https://inst.eecs.berkeley.edu/~ee240b/sp18/homeworks/hw3_soln.pdf

Prof. Tai-Haur Kuo, Analog IC Design ( 類比積體電路設計 ), Operational Amplifiers http://msic.ee.ncku.edu.tw/course/aic/201809/chapter5.pdf

B. Y. T. Kamath, R. G. Meyer and P. R. Gray, "Relationship between frequency response and settling time of operational amplifiers," in IEEE Journal of Solid-State Circuits, vol. 9, no. 6, pp. 347-352, Dec. 1974, doi: 10.1109/JSSC.1974.1050527.

P. R. Gray and R. G. Meyer, "MOS operational amplifier design-a tutorial overview," in IEEE Journal of Solid-State Circuits, vol. 17, no. 6, pp. 969-982, Dec. 1982, doi: 10.1109/JSSC.1982.1051851.

SERGIO FRANCO, Demystifying pole-zero doublets URL:https://www.edn.com/demystifying-pole-zero-doublets/