Bias Circuit

Posted on Edited on In

Curvature compensation

image-20240903234720200

Tutorials | 08012023 | 1.2.1 Bandgap Voltage Regular |, [https://youtu.be/dz067SOX0XQ?si=PlYczw9UdneAX6Na]

Subthreshold Conduction

By square-law, the Eq \(g_m = \sqrt{2\mu C_{ox}\frac{W}{L}I_D}\), it is possible to obtain a higer transconductance by increasing \(W\) while maintaining \(I_D\) constant. However, if \(W\) increases while \(I_D\) remains constant, then \(V_{GS} \to V_{TH}\) and device enters the subthreshold region. \[ I_D = I_0\exp \frac{V_{GS}}{\xi V_T} \]

where \(I_0\) is proportional to \(W/L\), \(\xi \gt 1\) is a nonideality factor, and \(V_T = kT/q\)

As a result, the transconductance in subthreshold region is \[ g_m = \frac{I_D}{\xi V_T} \]

which is \(g_m \propto I_D\)

image-20240627230726326

image-20240627230744044

PTAT with subthreshold MOS

MOS working in the weak inversion region ("subthreshold conduction") have the similar characteristics to BJTs and diodes, since the effect of diffusion current becomes more significant than that of drift current

image-20240803193343915

image-20240803195500321

image-20240803200129592

Hongprasit, Saweth, Worawat Sa-ngiamvibool and Apinan Aurasopon. "Design of Bandgap Core and Startup Circuits for All CMOS Bandgap Voltage Reference." Przegląd Elektrotechniczny (2012): 277-280.

VBE

  • temperature coefficient of \(V_{BE}\) itself depends on the temperature,

  • temperature coefficient of the \(V_{BE}\) at a given temperature T depends on the magnitude of \(V_{BE}\) itself

\(\frac{kT}{q}\) is approximately 26mV, at room temperature 300K

In advanced node, N4P, \(V_{BE}\) is about -1.45mV/K

constant-gm

aka. Beta-multiplier reference

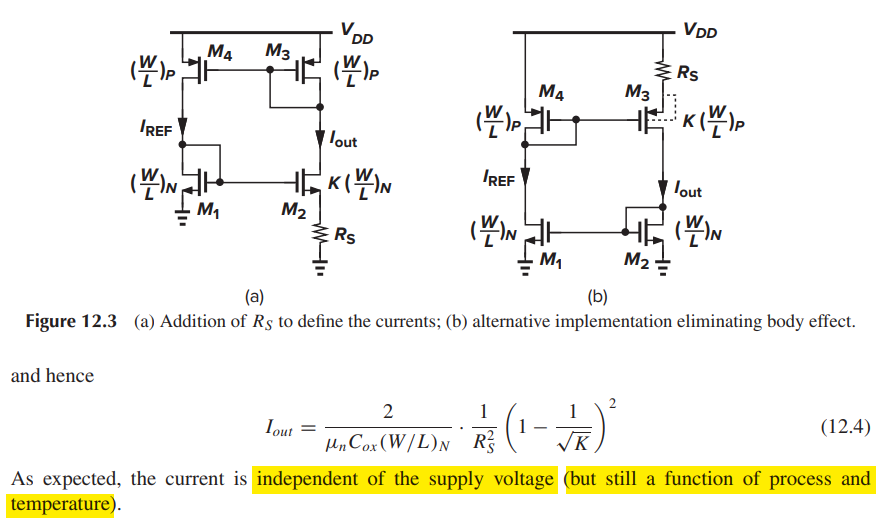
image-20240803155734754

\(I_\text{out}\) is PTAT in case temperature coefficient of \(R_s\) is less than that of \(\mu_n\)

image-20240803201548623

Body effect of M2

image-20240803201803449

image-20240803202015668

image-20240803201941683

image-20231213235846243

Boris Murmann, Systematic Design of Analog Circuits Using Pre-Computed Lookup Tables

S. Pavan, "Systematic Development of CMOS Fixed-Transconductance Bias Circuits," in IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 69, no. 5, pp. 2394-2397, May 2022

S. Pavan, "A Fixed Transconductance Bias Circuit for CMOS Analog Integrated Circuits", IEEE International Symposium on Circuits and Systems, ISCAS 2004, Vancouver , May 2004

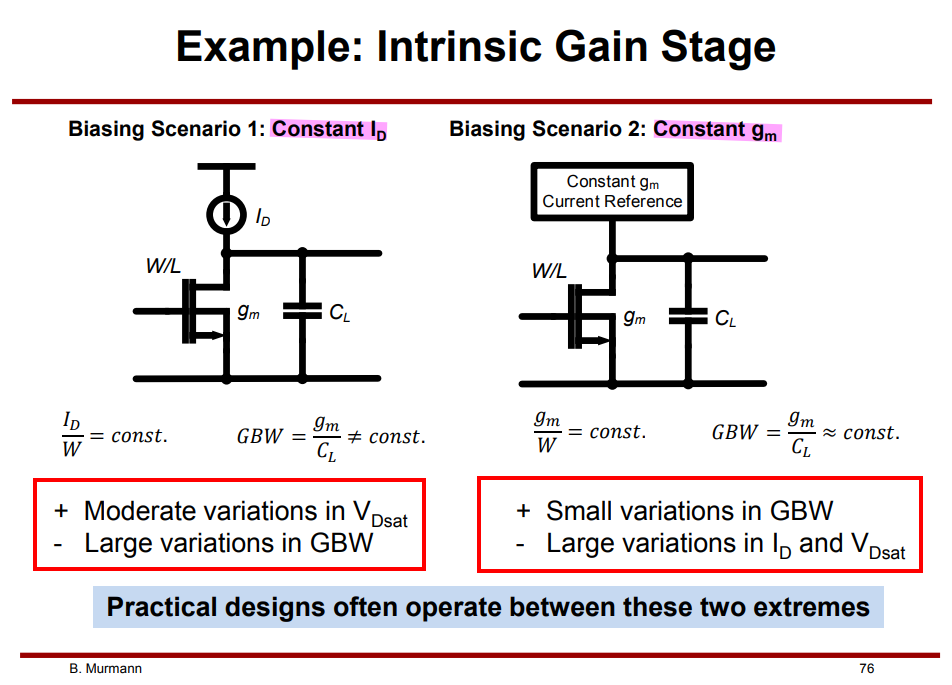
Why MOS in saturation ?

\(g_m\), \(g_\text{ds}\) at fixed \(V_\text{GS}\)

image-20231125224714658

\(g_{ds}\) is constant in saturation region

in triode region \[ g_{ds} = \mu_nC_{ox}\frac{W}{L}(V_{GS}-V_{TH}-V_{DS}) \]

Interestingly, \(g_m\) in the saturation region is equal to the inverse of \(R_\text{on}\) in the deep triode region.

gds_vgs.drawio

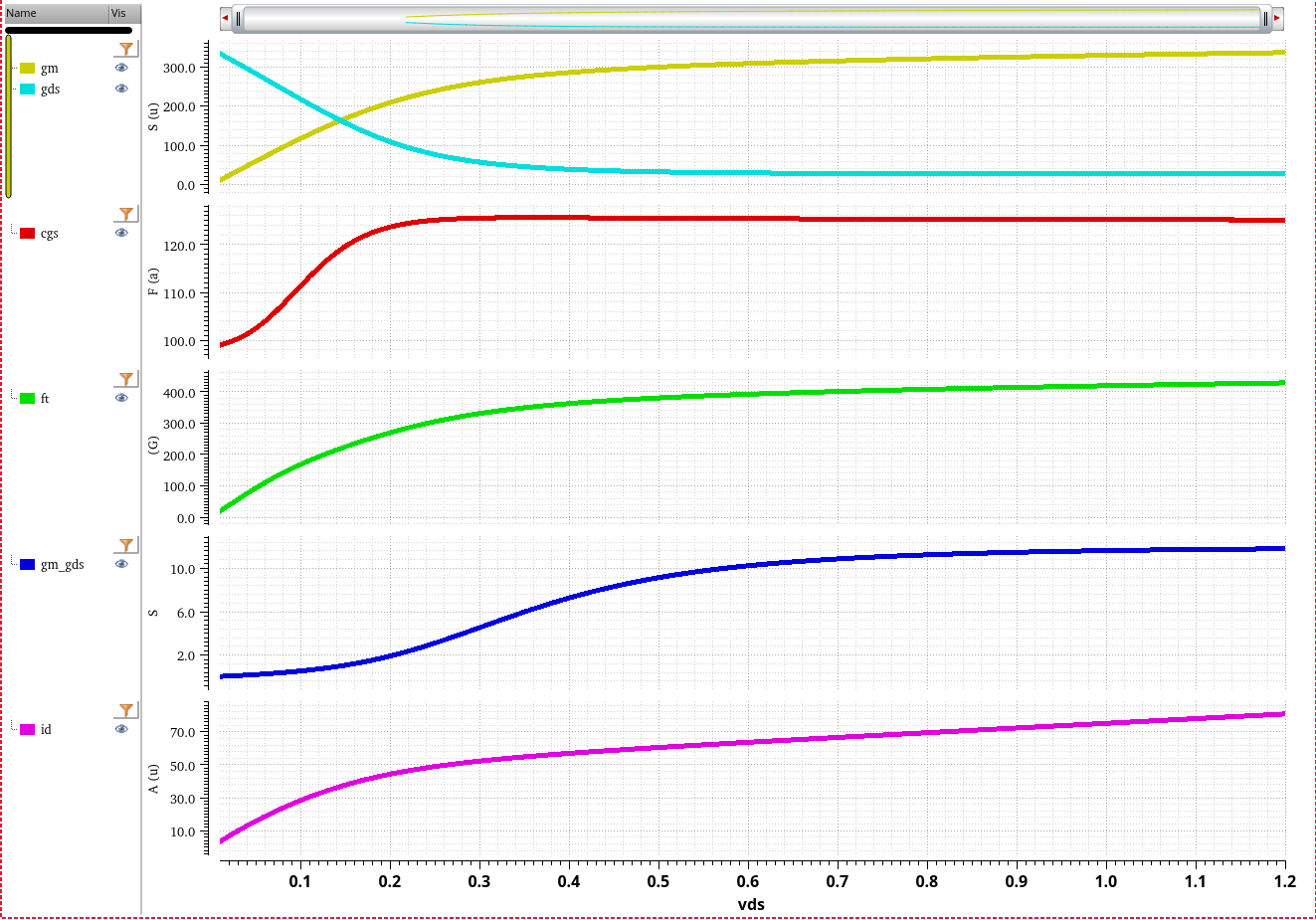
image-20240727140918647

\(g_m\), \(g_\text{ds}\) at fixed \(I_d\), \(V_G\)

In triode region \[ I_D = \frac{1}{2}\mu_nC_{ox}\frac{W}{L}[2(V_{GS}-V_{TH})V_{DS}-V_{DS}^2] \] where \(I_D\) and \(V_G\) is fixed

Then \(V_S\) can be expressed with \(V_D\), that is \[ V_S = V_{GT} - \sqrt{(V_{GT}-V_D)^2+V_{dsat}^2} \] where \(V_{GT}=V_G-V_{TH}\), \(V_{dsat}\) is \(V_{DS}\) saturation voltage \[ g_m = \mu_nC_{ox}\frac{W}{L}\left(V_D-V_{GT}+\sqrt{(V_{GT}-V_D)^2+V_{dsat}^2}\right) \] Then \[ \frac{\partial g_m}{\partial V_D} \propto 1 - \frac{V_{GT}-V_D}{\sqrt{(V_{GT}-V_D)^2+V_{dsat}^2}} \gt 0 \]

That is, \(g_m \propto V_D\)​

\[\begin{align} g_{ds} &= \mu_nC_{ox}\frac{W}{L}(V_{GS}-V_{TH}-V_{DS}) \\ &= \mu_nC_{ox}\frac{W}{L}(V_{GT}-V_{D}) \end{align}\]

That is, \(g_{ds} \propto -V_D\)

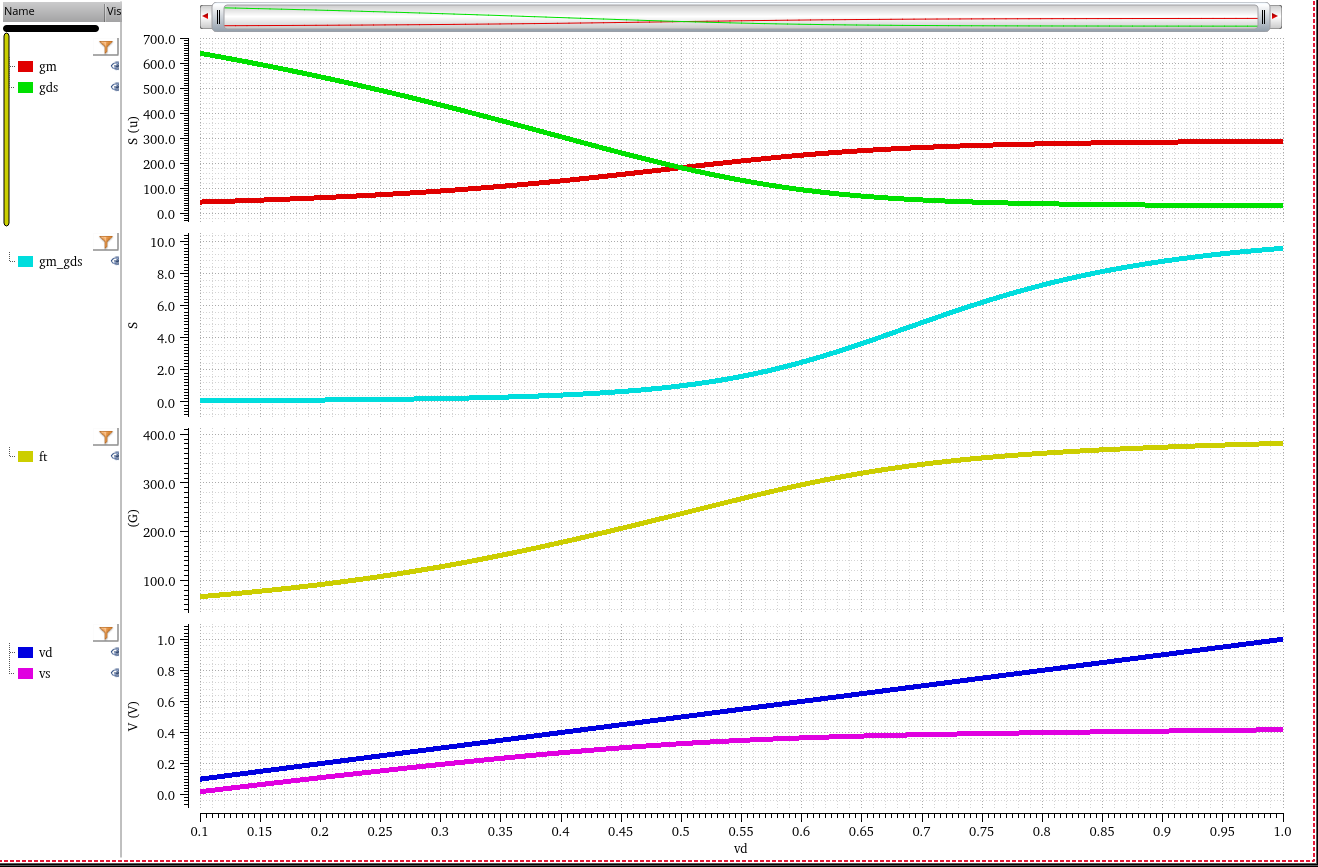
image-20240727171005401

Both gain and speed degrade once entering triode region, though Id is constant

Cascode MOS

The low threshold voltage of cascode MOS don't help decrease the minimum output voltage

cascode_vth.drawio

Channel-length modulation

❗ There it not channel-length modulation in the triode region

image-20240727095651984

\[\begin{align} I_D &=\frac{1}{2}\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_{TH})^2(1+\frac{\Delta L}{L}) \\ I_D &=\frac{1}{2}\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_{TH})^2(1+\lambda V_{DS}) \\ I_D &=\frac{1}{2}\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_{TH})^2(1+\frac{V_{DS}}{V_A}) \end{align}\]

where \(\frac{\Delta L}{L}=\lambda V_{DS}\) and \(V_A=\frac{1}{\lambda}\)

\(\lambda\) is channel length modulation parameter

\(V_A\), i.e. Early voltage is equal to inverse of channel length modulation parameter

The output resistance \(r_o\)

\[\begin{align} r_o &= \frac{\partial V_{DS}}{\partial I_D} \\ &= \frac{1}{\partial I_D/\partial V_{DS}} \\ &= \frac{1}{\lambda I_D} \\ &= \frac{V_A}{I_D} \end{align}\]

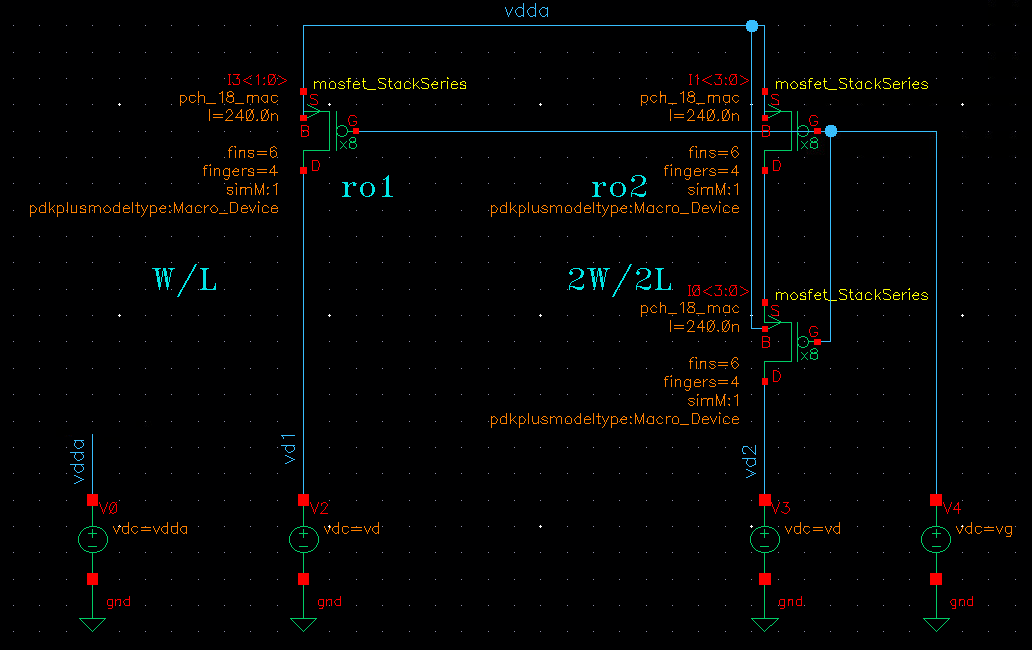
Due to \(\lambda \propto 1/L\), i.e. \(V_A \propto L\) \[ r_o \propto \frac{L}{I_D} \] image-20220930001909262

image-20220930002003924

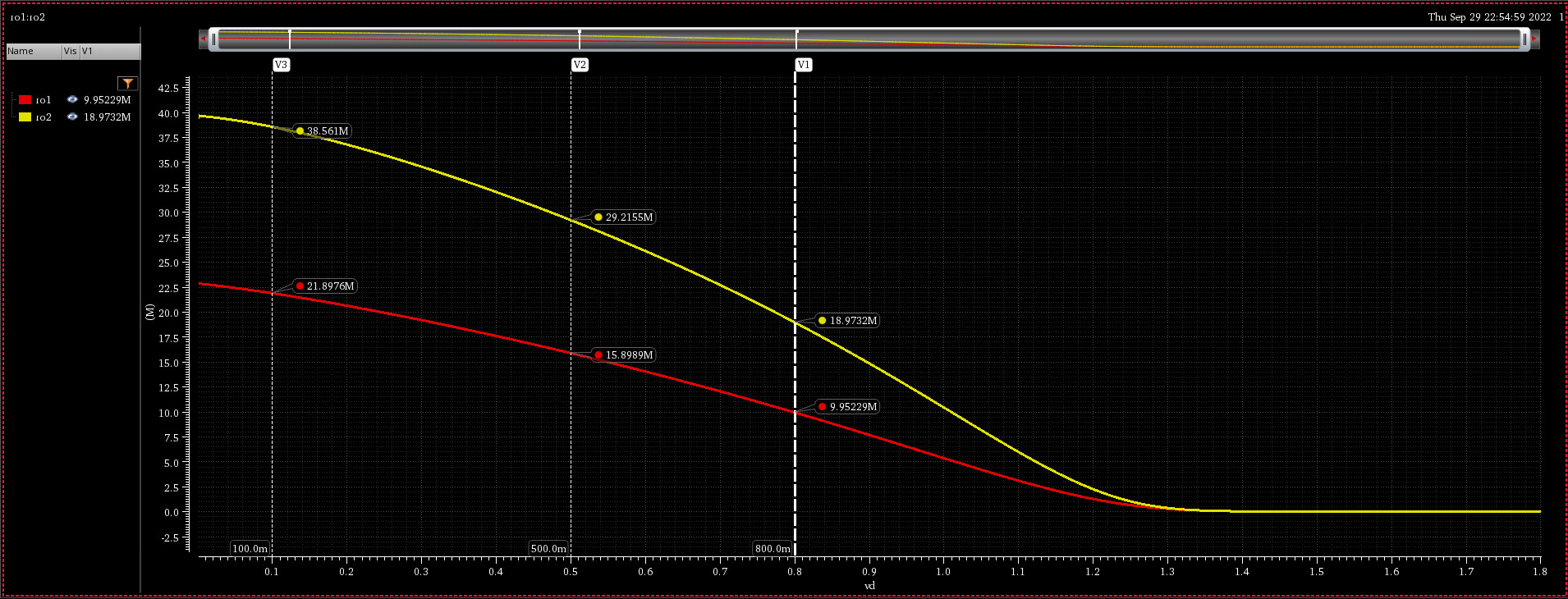
image-20220930002157365

The output resistance is almost doubled using Stacked FET in saturation region

\(V_t\) and mobility \(\mu_{n,p}\) are sensitive to temperature

  • \(V_t\) decreases by 2-mV for every 1\(^oC\) rise in temperature
  • mobility \(\mu_{n,p}\) decreases with temperature

Overall, increase in temperature results in lower drain currents

current mirror mismatch

The current mismatch consists of two components.

  • The first depends on threshold voltage mismatch and increases as the overdrive \((V_{GS} − V_t)\) is reduced.
  • The second is geometry dependent and contributes a fractional current mismatch that is independent of bias point.

\[ \Delta I_D = g_m\cdot \Delta V_{TH}+I_D\cdot \frac{\Delta(W/L)}{W/L} \]

where mismatches in \(\mu_nC_{ox}\) are neglected

\[\begin{align} \Delta V_{TH} &= \frac{A_{VTH}}{\sqrt{WL}} \\ \frac{\Delta(W/L)}{W/L} &= \frac{A_{WL}}{\sqrt{WL}} \end{align}\]

summary:

Size \(g_m\) \(\Delta V_{TH}\) \(\frac{\Delta(W/L)}{W/L}\) mismatch (%) simu (%)
W, L 1 1 1 \(I_{\Delta_{V_{TH}}}+I_{\Delta_{WL}}\) 3.44
W, 2L \(1/\sqrt{2}\) \(1/\sqrt{2}\) \(1/\sqrt{2}\) \(I_{\Delta_{V_{TH}}}/2+I_{\Delta_{WL}}/\sqrt{2}\) 1.98
2W, L \(\sqrt{2}\) \(1/\sqrt{2}\) \(1/\sqrt{2}\) \(I_{\Delta_{V_{TH}}}+I_{\Delta_{WL}}/\sqrt{2}\) 2.93
We get \(I_{\Delta_{V_{TH}}}\simeq 1.71\%\) and \(I_{\Delta_{WL}} \simeq 1.73\%\)

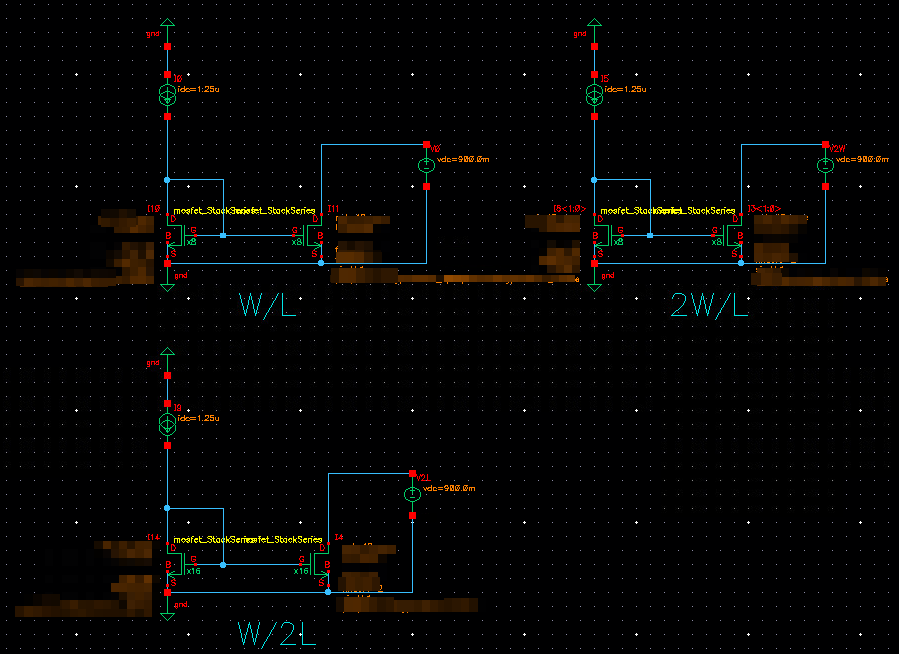
image-20221003001056211

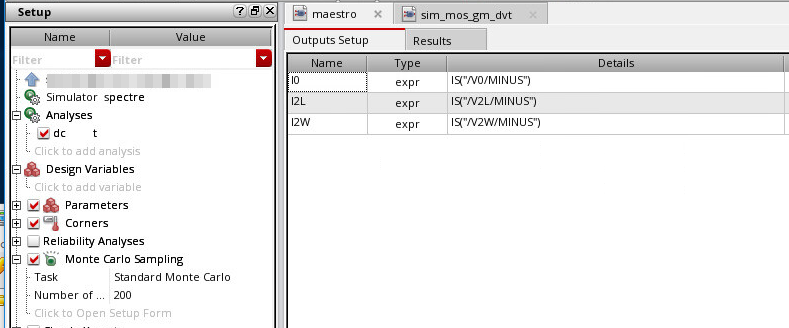
image-20221002215942456

Biasing current source and global variation Monte Carlo

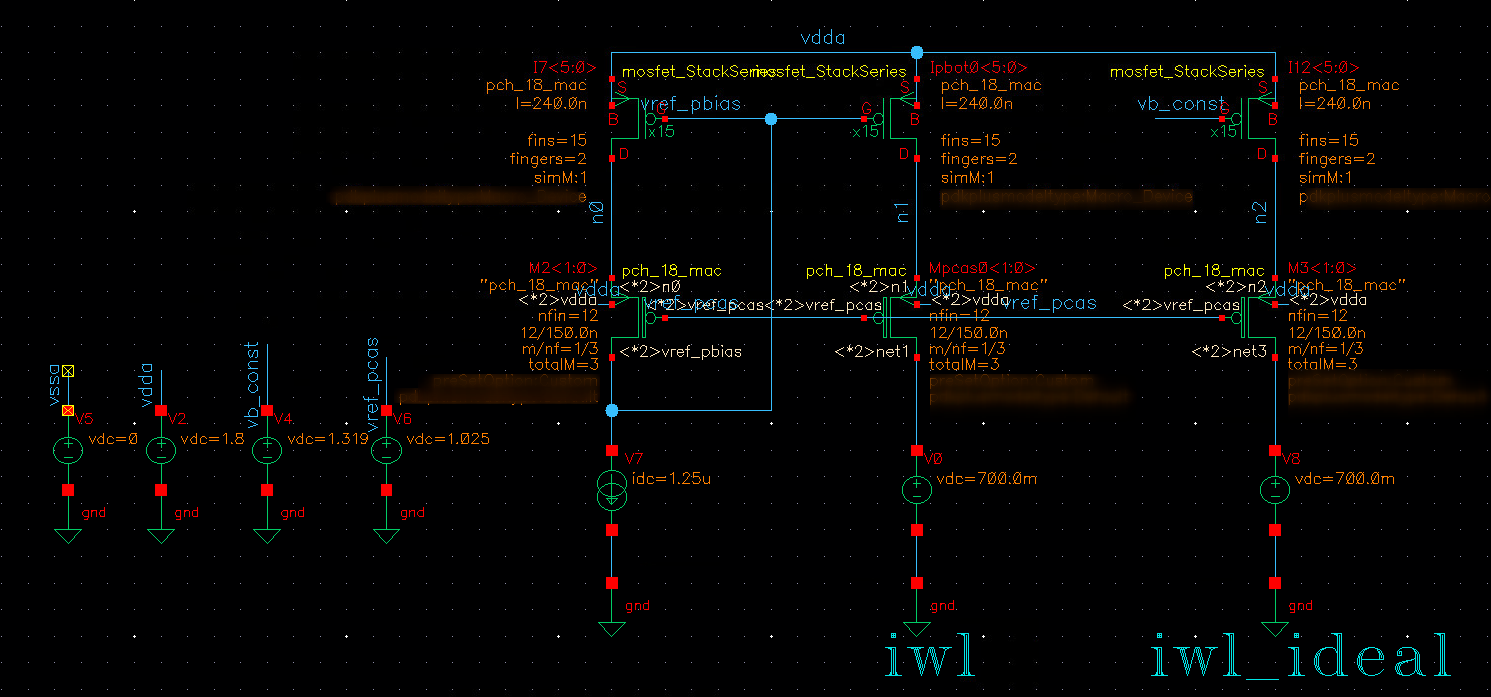
image-20221020225334767

image-20221020225502503

iwl: biased by mirror

iwl_ideal: biased by vdc source, whose value is typical corner

For local variation, constant voltage bias (vb_const in schematic) help reduce variation from \(\sqrt{2}\Delta V_{th}\) to \(\Delta V_{th}\)

For global variation, all device have same variation, mirror help reduce variation by sharing same \(V_{gs}\)

  1. global variation + local variation (All MC)

image-20221020225615633

  1. local variation (Mismatch MC)

image-20221020225701218

  1. global variation (Process MC)

image-20221020232515420

We had better bias mos gate with mirror rather than the vdc source while simulating sub-block.

This is real situation due to current source are always biased by mirror and vdc biasing don't give the right result in global variation Monte Carlo simulation (542.8n is too pessimistic, 13.07p is right result)

Operating points & Small gain theorem

Dr. Degang Chen, EE 501: CMOS Analog Integrated Circuit Design [https://class.ece.iastate.edu/djchen/ee501/2020/References.ppt]

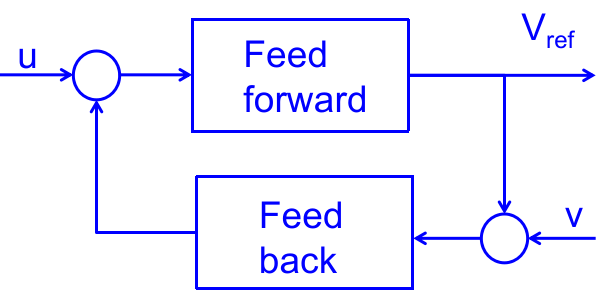
image-20231202102259692

For any given constant values of u and v, the constant values of variables that solve the the feed back relationship are called the operating points, or equilibrium points.

Operating points can be either stable or unstable.

An operating point is unstable if any or some small perturbation near it causes divergence away from that operating point.

If the loop gain evaluated at an operating point is less than one, that operating point is stable.

This is a sufficient condition

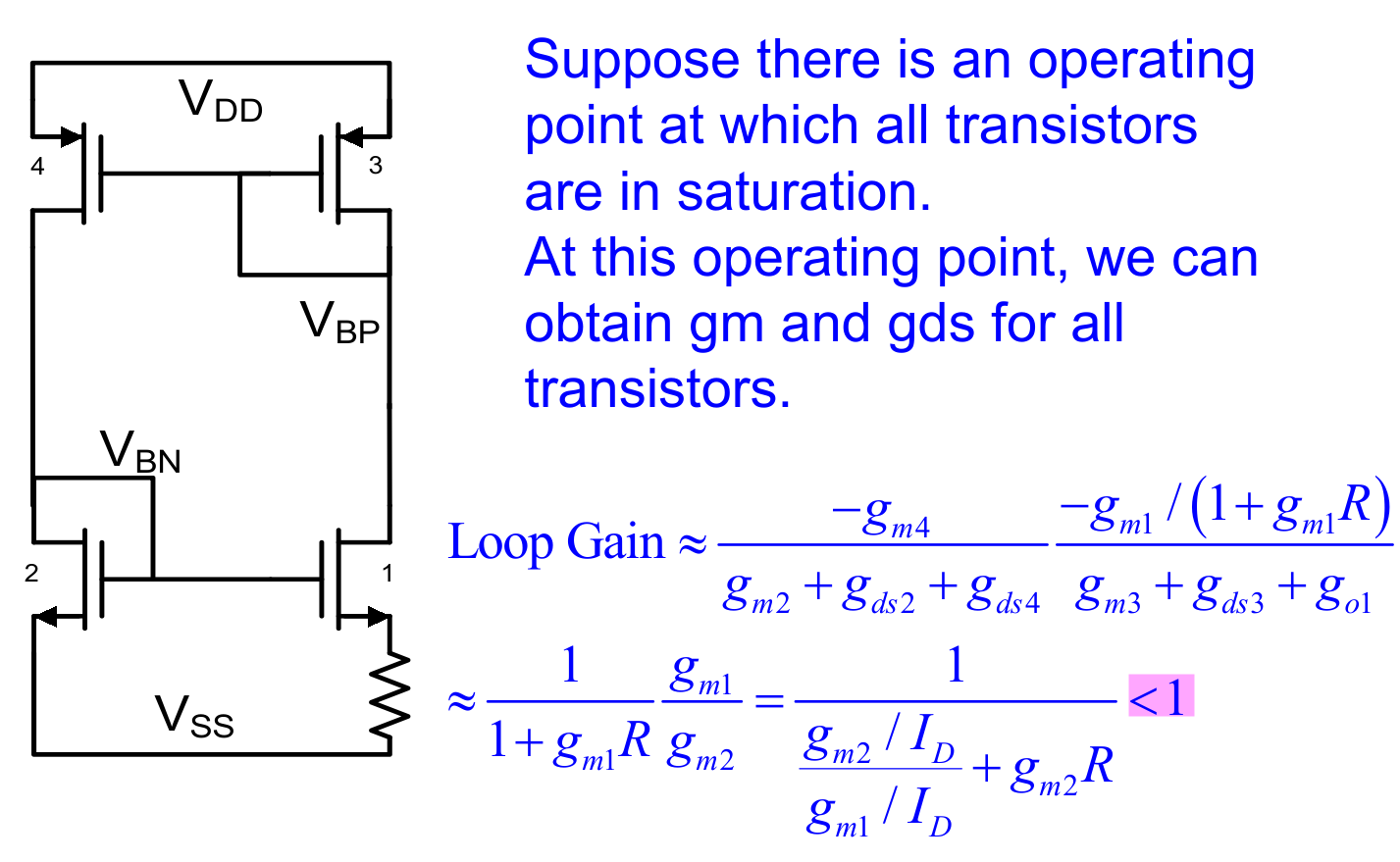
image-20231202105749888

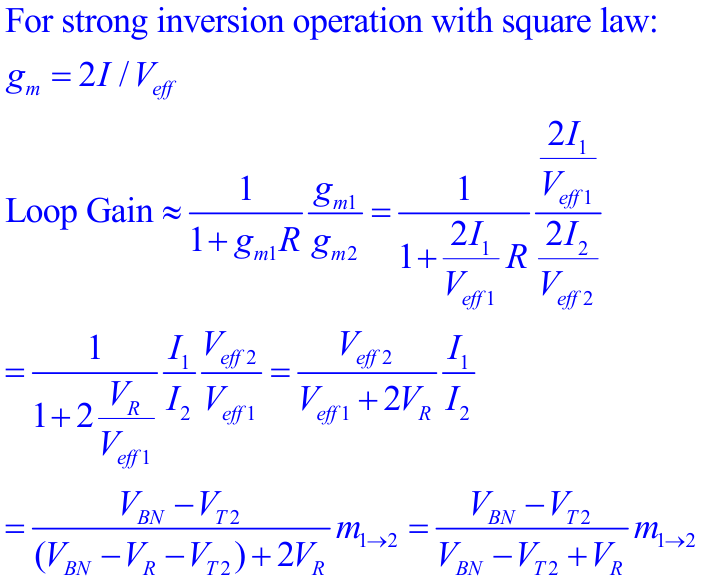
image-20231202105621385

With \(m_{1\to 2} = 1\) \[ \text{Loop Gain} \simeq \frac{V_{BN}-V_{T2}}{V_{BN}-V_{T2} + V_R} \tag{LG\_0} \] Assuming all MOS in strong inv operation, \(I\), \(V_{BN}\) and \(V_R\) is obtain \[\begin{align} I &= \frac{2\beta _1 + 2\beta _2 - 4\sqrt{\beta _1 \beta _2}}{R^2\beta _1 \beta _2} \\ V_{BN} &= V_{T2} + \frac{2}{R\beta _2}(1- \sqrt{\frac{\beta _2}{\beta _1}}) \\ IR &= \frac{2}{R}\left( \frac{1}{\sqrt{\beta_2}} - \frac{1}{\sqrt{\beta_1}} \right) \end{align}\]

Substitute \(V_{BN}\) and \(V_R\) of \((LG\_0)\) \[\begin{align} \text{Loop Gain} & \simeq \frac{1-\sqrt{\frac{\beta_2}{\beta_1}}}{\frac{\beta_2}{\beta_1} - 3\sqrt{\frac{\beta_2}{\beta_1}}+2} \\ &= \frac{1}{2-\sqrt{\frac{\beta_2}{\beta_1}}} \tag{LG\_1} \end{align}\]

Alternative approach for Loop Gain

using derivation of large signal

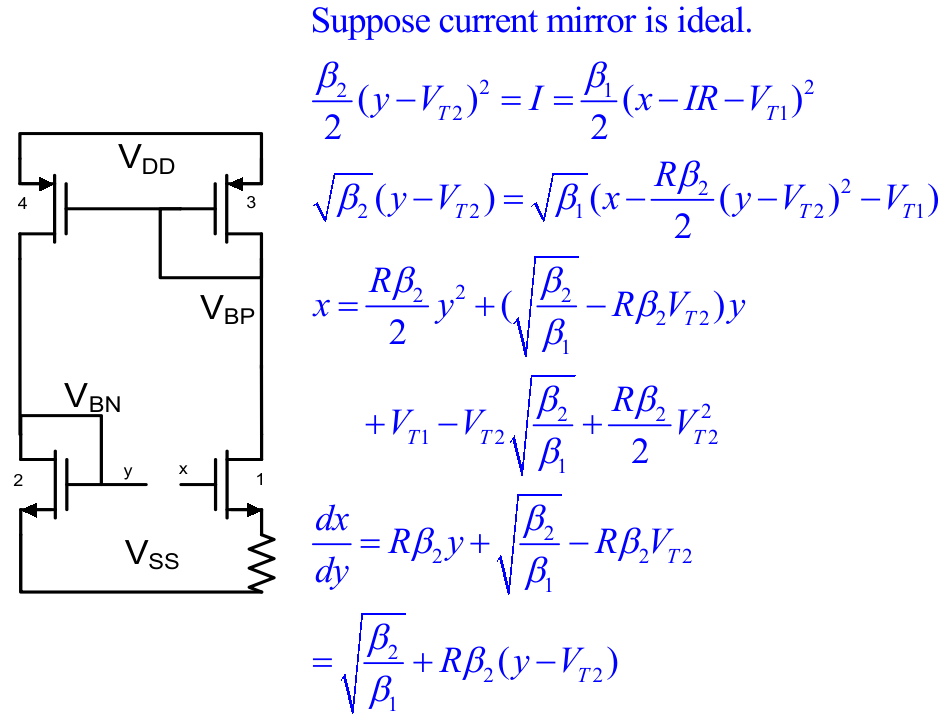
image-20231202132310478

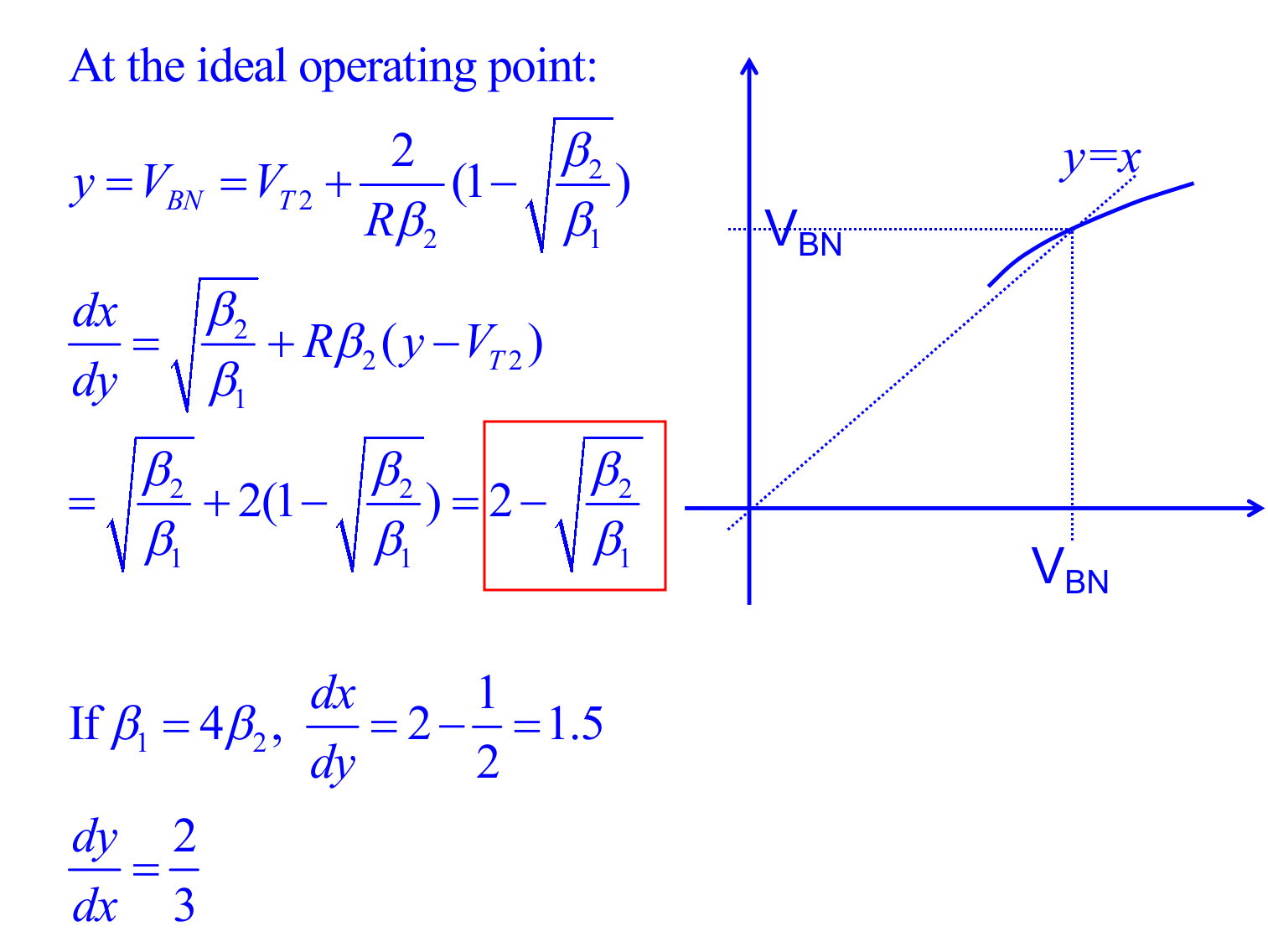
image-20231202134138319

❗❗❗ R should not be on the other side

image-20231202104505264

Self-Biasing Cascode

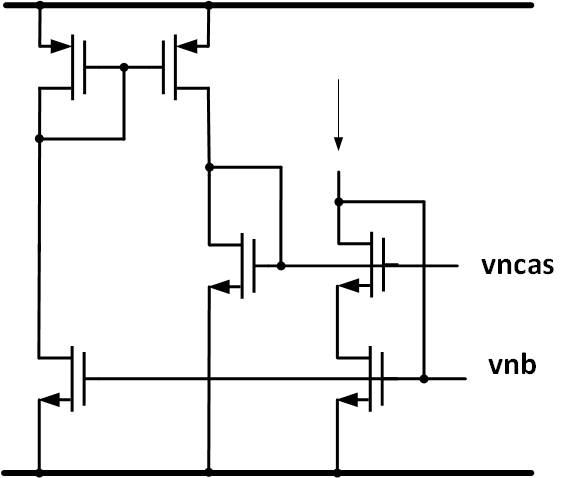
image-20231212153054247

cascode_selfbias.drawio

v2i.drawio

cap network

pi_Cap.drawio

\[\begin{align} (V_a-V_{a0})C_0 + (\overline{V_a - V_b} - \overline{V_{a0} - V_{b0}})C_1 &= \Delta Q_a \\ (V_b-V_{b0})C_0 + (\overline{V_b - V_a} - \overline{V_{b0} - V_{a0}})C_1 &= \Delta Q_b \end{align}\]

therefore we obtain \[\begin{align} V_a + V_b &= \frac{\Delta Q_a + \Delta Q_b}{C_0} + V_{a0} + V_{b0} \\ V_a - V_b &= \frac{\Delta Q_a - \Delta Q_b}{C_0+2C_1} + V_{a0} - V_{b0} \end{align}\] Then \[\begin{align} V_a &= \frac{\Delta Q_a(C_0+C_1)+\Delta Q_b C_1}{C_0(C_0+2C_1)} + V_{a0} \\ V_b &= \frac{\Delta Q_aC_1+\Delta Q_b (C_0+C_1)}{C_0(C_0+2C_1)} + V_{b0} \end{align}\]

rearrange the above equation \[\begin{align} V_a &= \frac{\Delta Q_a}{C_0} + \frac{\Delta Q_b-\Delta Q_a}{C_0(\frac{C_0}{C_1}+2)} + V_{a0} \\ V_b &= \frac{\Delta Q_b}{C_0} + \frac{\Delta Q_a-\Delta Q_b}{C_0(\frac{C_0}{C_1}+2)} + V_{b0} \end{align}\]

The difference between \(V_a\) and \(V_b\) \[ V_a - V_b = \frac{I_a-I_b}{C_0+2C_1}t + V_{a0} - V_{b0} \]

\(C_1\) save total capacitor area while obtaining same \(V_a - V_b\) due to \(\Delta I_{a,b}\) corresponding to \(C_0\)

at autozero phase \[\begin{align} I_{a0} &= \frac{1}{2}\mu C_{OX}\frac{W}{L}(V_{a0} - V_{TH})^2 \\ I_{Rb} &= \frac{1}{2}\mu C_{OX}\frac{W}{L}(V_{b0} - V_{TH})^2 \end{align}\]

then \[ \Delta I_0 = \frac{1}{2}(V_{a0} - V_{b0})(g_{m,a0}+g_{m,b0}) \] where \(g_{m,a0}+g_{m,b0} = \mu C_{OX}\frac{W}{L}(V_{a0}+V_{b0} - 2V_{TH})\)

at comparison phase \[\begin{align} I_{a1} &= \frac{1}{2}\mu C_{OX}\frac{W}{L}(V_{a1} - V_{TH})^2 \\ I_{b1} &= \frac{1}{2}\mu C_{OX}\frac{W}{L}(V_{b1} - V_{TH})^2 \end{align}\]

then \[ \Delta I_1 = \frac{1}{2}(V_{a1} - V_{b1})(g_{m,a1}+g_{m,b1}) \] That is, \(g_{m,a1}+g_{m,b1} = \mu C_{OX}\frac{W}{L}(V_{a1}+V_{b1} - 2V_{TH})\)

To minimize the difference between \(\Delta I_1\) and \(\Delta I_0\), the drift of both differential and common mode between \(V_a\) and \(V_b\) shall be alleviated

reference

B. Razavi, "The Design of a Low-Voltage Bandgap Reference [The Analog Mind]," in IEEE Solid-State Circuits Magazine, vol. 13, no. 3, pp. 6-16, Summer 2021, doi: 10.1109/MSSC.2021.3088963