Data Converter
1-bit DAC
TODO 📅
\(\Delta \Sigma\) ADC: Linearity
!!PD: Non-linear
Dan Boschen Why use a 1-bit ADC in a Sigma Delta Modulator?. [https://dsp.stackexchange.com/questions/53059/why-use-a-1-bit-adc-in-a-sigma-delta-modulator#comment105988_53063]
Evaluating DAC
Walt Kester. Evaluating High Speed DAC Performance [https://www.analog.com/media/en/training-seminars/tutorials/mt-013.pdf]
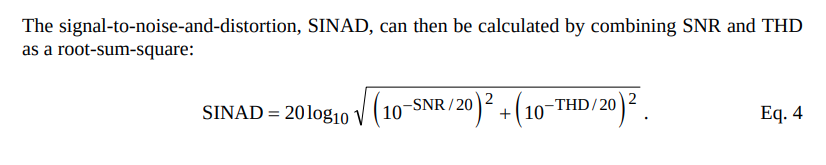
THD
EE315B VLSI Data Conversion Circuits [pdf]
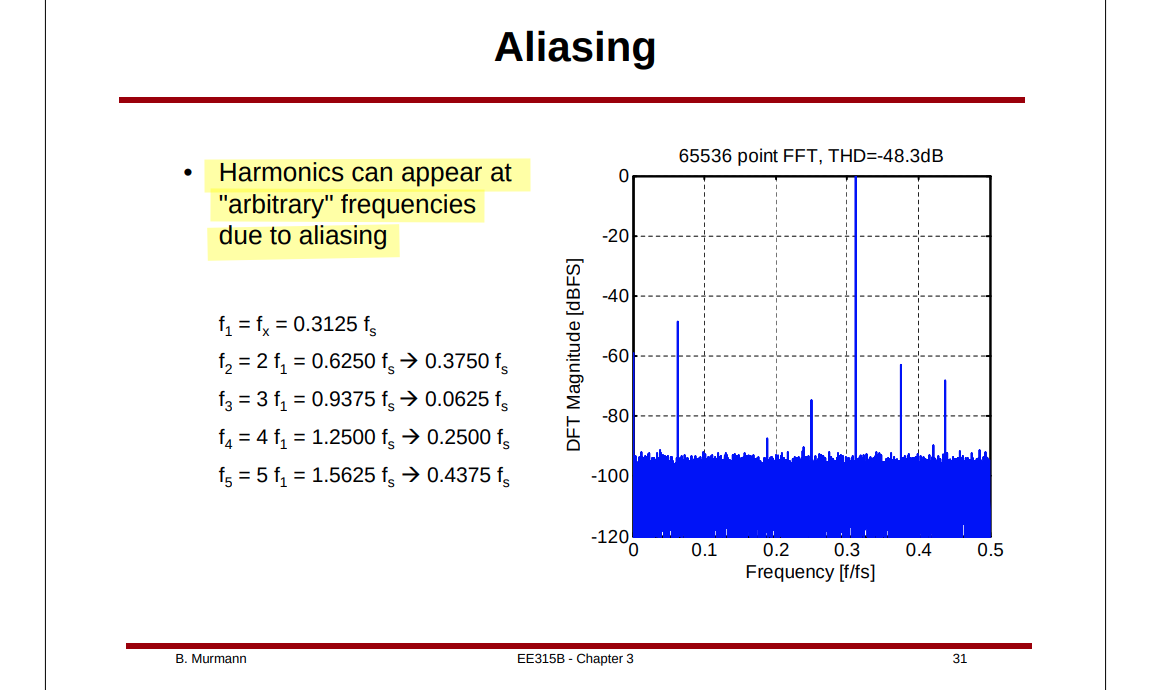
Harmonics can appear at "arbitrary" frequencies due to aliasing
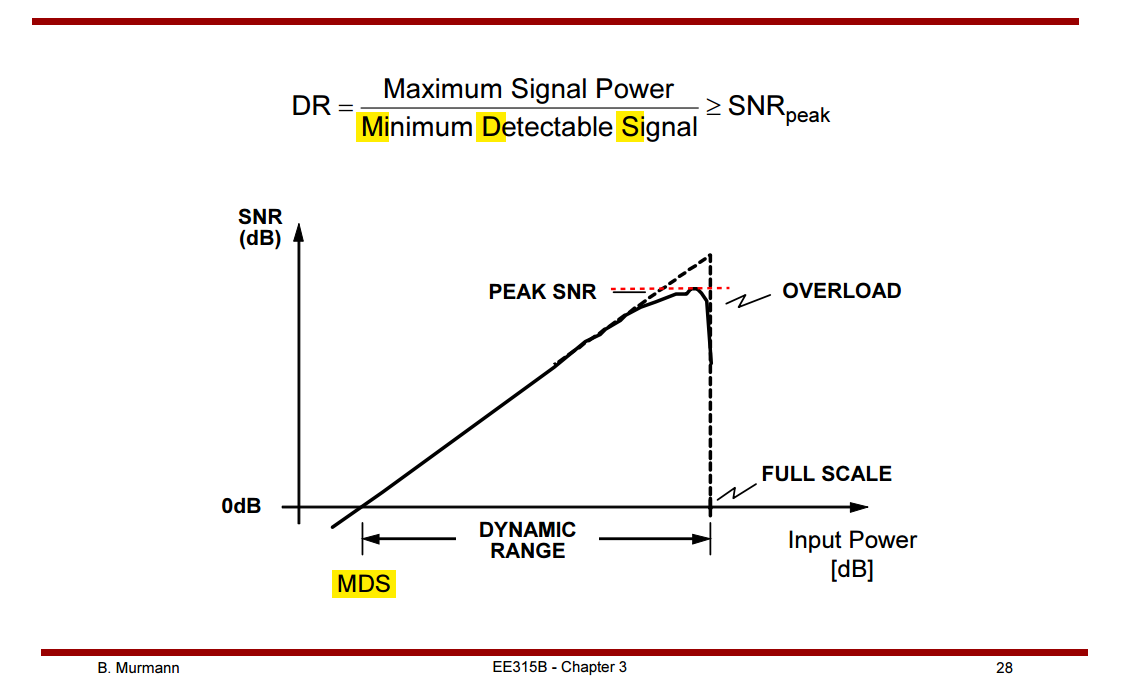
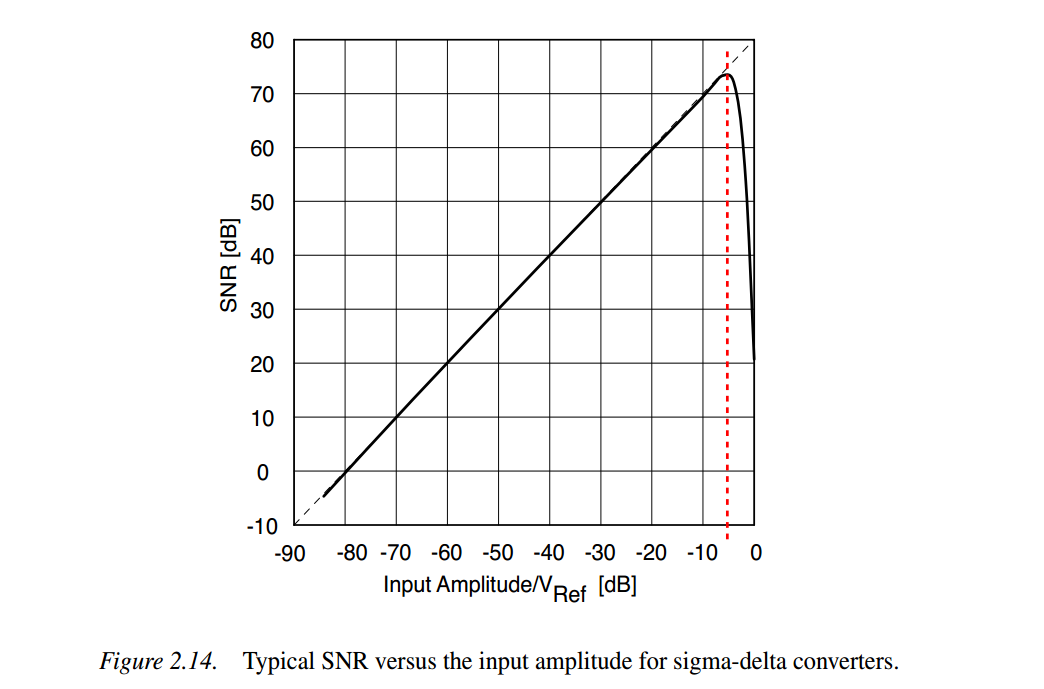
Dynamic Range

\[ \text{SNR} = 10\log\left(\frac{V_\text{in}^2/2}{\Delta^2/12}\right) \]
FoMs
B. Murmann, "ADC Performance Survey 1997-2022," [Online]. Available: [https://github.com/bmurmann/ADC-survey]
Carsten Wulff, "Advanced Integrated Circuits 2025" [http://analogicus.com/aic2025/2025/02/20/Lecture-6-Oversampling-and-Sigma-Delta-ADCs.html#high-resolution-fom]

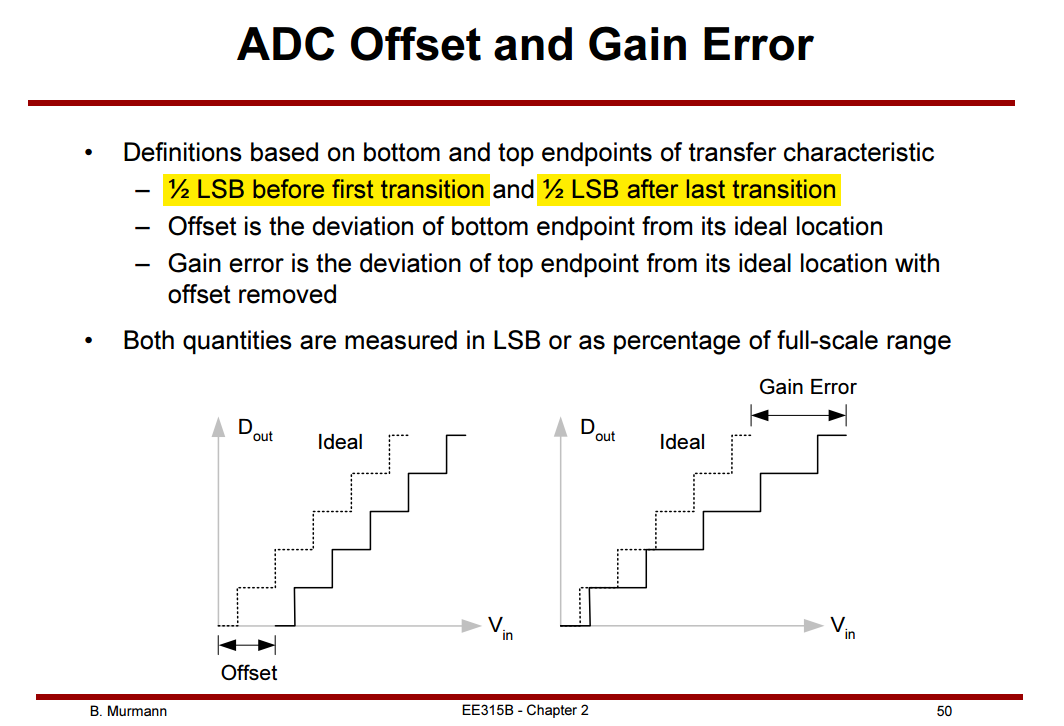
Offset & Gain Error

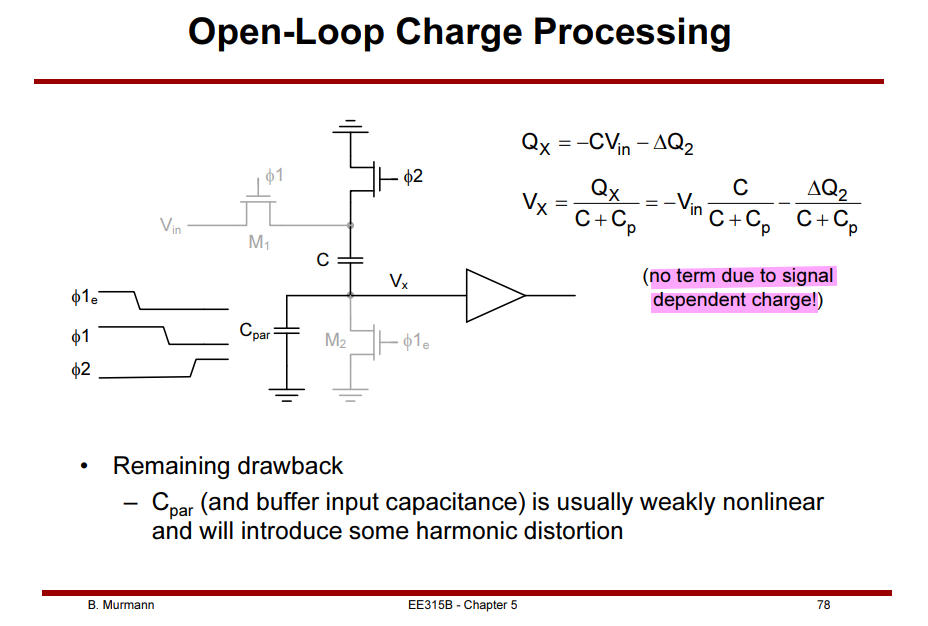
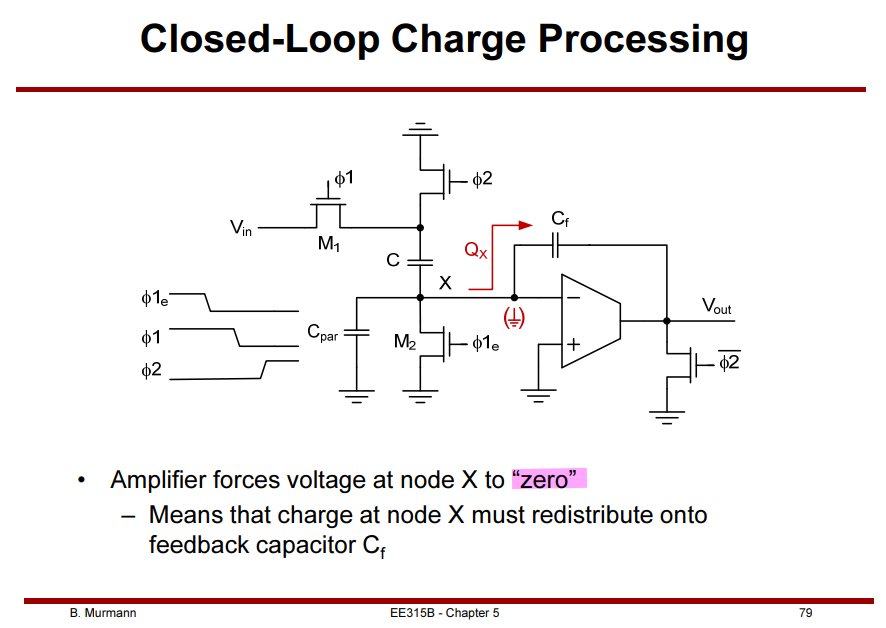
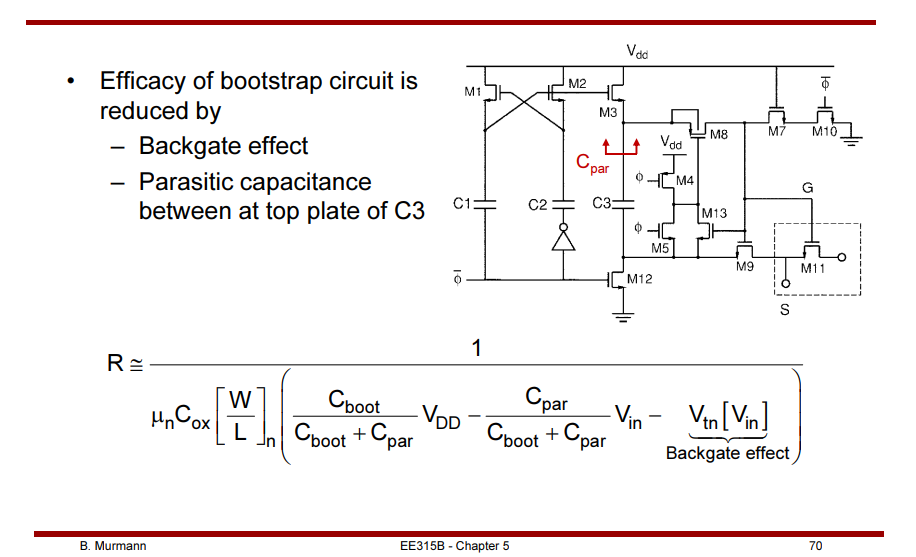
Charge Injection and Clock Feedthrough
Slow Gating, Fast Gating
TODO 📅
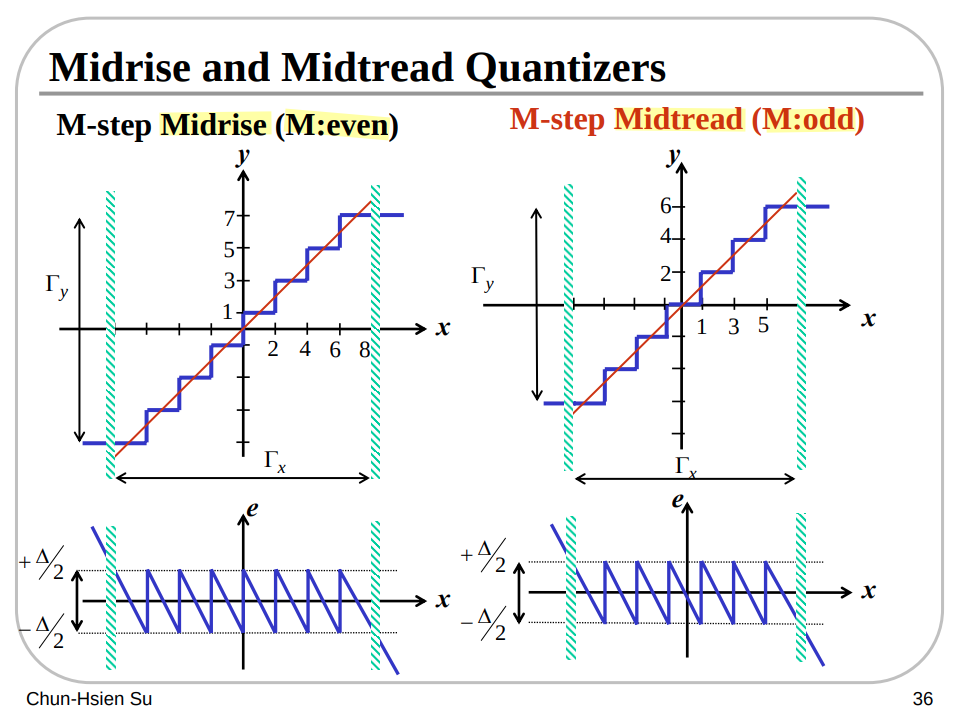
Midrise and Midtread Quantizers
\(\Gamma_x\) is no-overload range

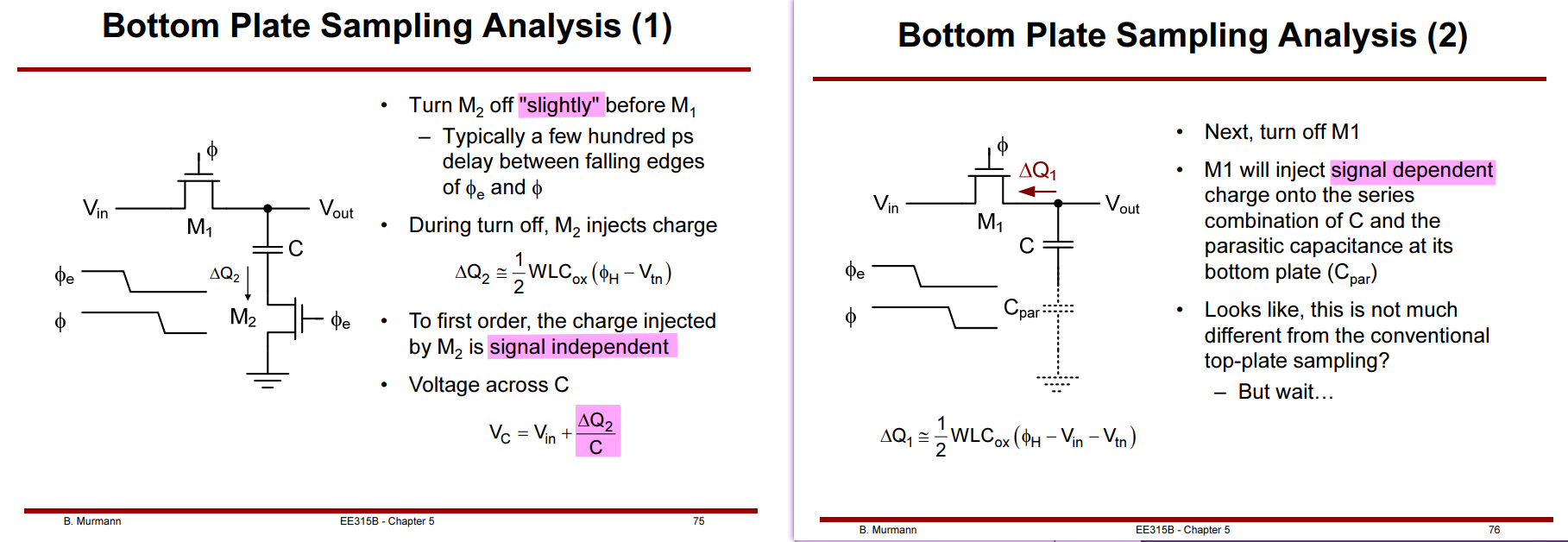
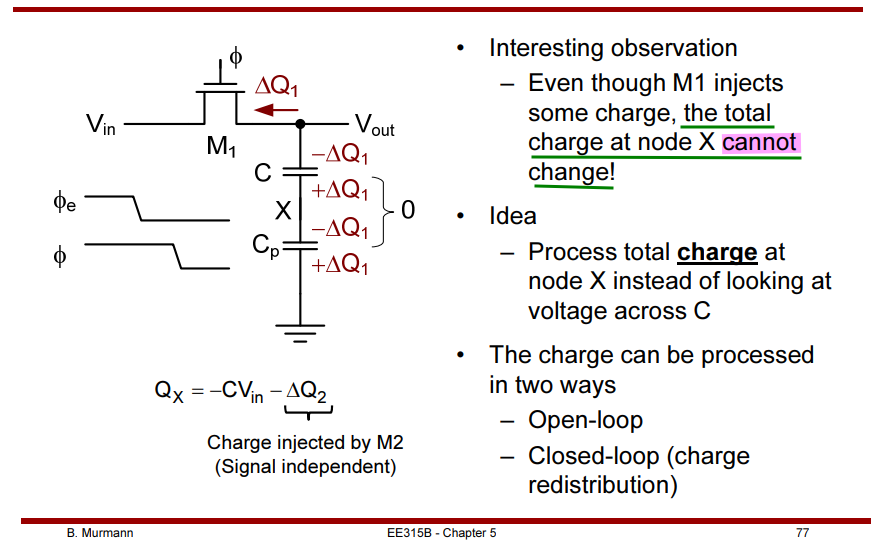
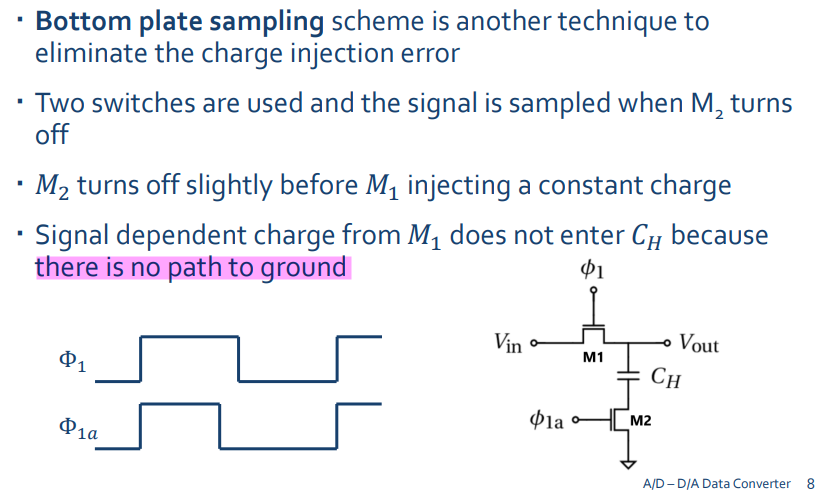
Top-Plate vs Bottom-Plate Sampling
[https://class.ece.iastate.edu/ee435/lectures/EE%20435%20Lect%2044%20Spring%202008.pdf]
Bottom-Plate Sampling
Sample signal at the "grounded" side of the capacitor to achieve signal independent sampling

EE 435 Spring 2024 Analog VLSI Circuit Design - Switched-Capacitor Amplifiers Other Integrated Filters, https://class.ece.iastate.edu/ee435/lectures/EE%20435%20Lect%2044%20Spring%202008.pdf
Top-Plate Sampling
TODO 📅
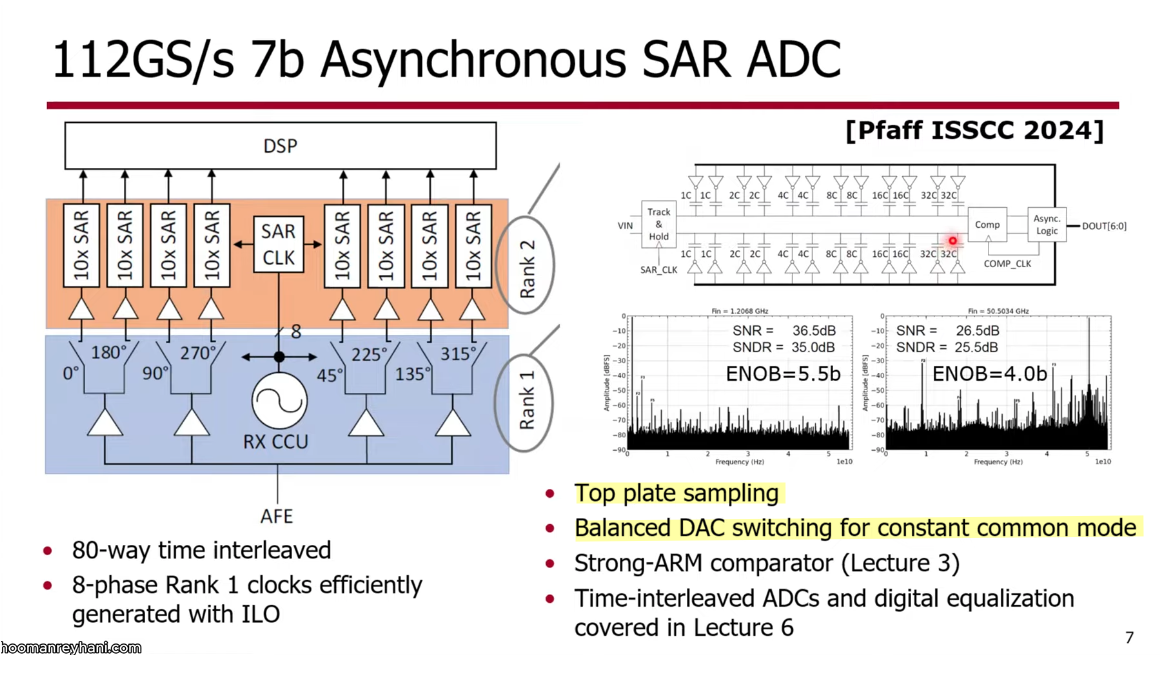
Maintain constant common-mode during conversion
D. Pfaff et al., "7.3 A 224Gb/s 3pJ/b 40dB Insertion Loss Transceiver in 3nm FinFET CMOS," 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 2024 [https://iccircle.com/static/upload/img20240529101747.pdf]
—, "A 224Gb/s 3pJ/bit 42dB Insertion Loss Post-FEC Error Free Transceiver in 3-nm FinFET CMOS (Invited)," 2025 IEEE Custom Integrated Circuits Conference (CICC), Boston, MA, USA, 2025, pp. 1-8, doi: 10.1109/CICC63670.2025.10983461.
E. Swindlehurst et al., "An 8-bit 10-GHz 21-mW Time-Interleaved SAR ADC With Grouped DAC Capacitors and Dual-Path Bootstrapped Switch," IEEE Journal of Solid-State Circuits, vol. 56, no. 8, pp. 2347-2359, 2021, [https://sci-hub.se/10.1109/JSSC.2021.3057372]
SFDR & INL
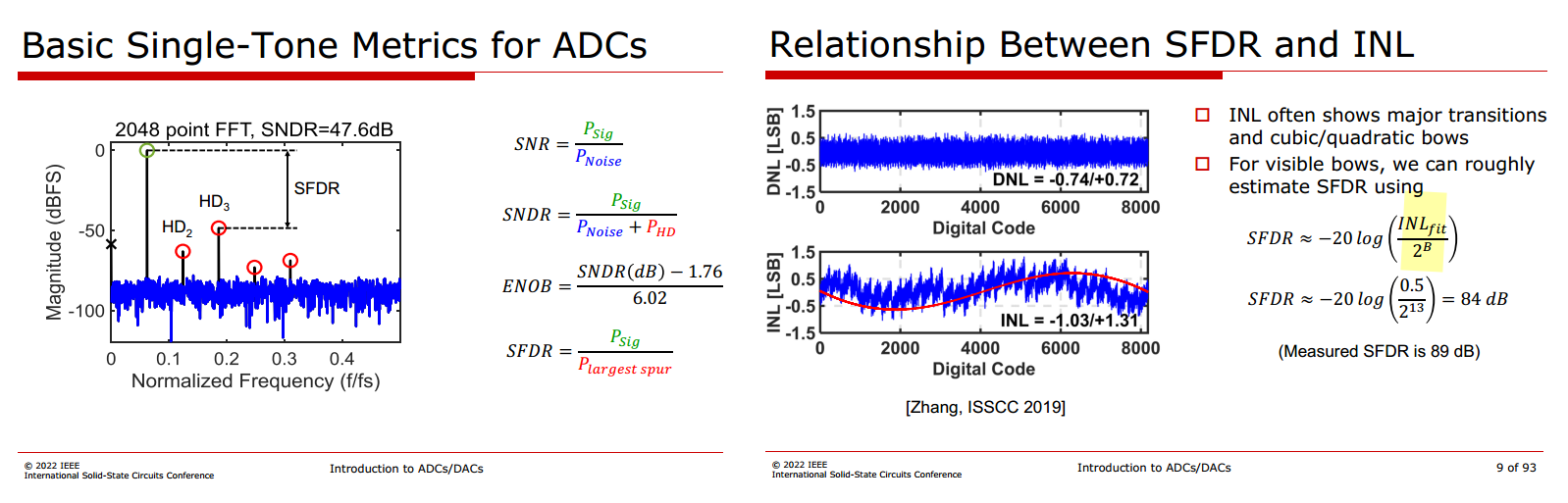
Beware, this is of course only true under the same conditions at which the INL was taken, i.e. typically low input signal frequency
Track Time
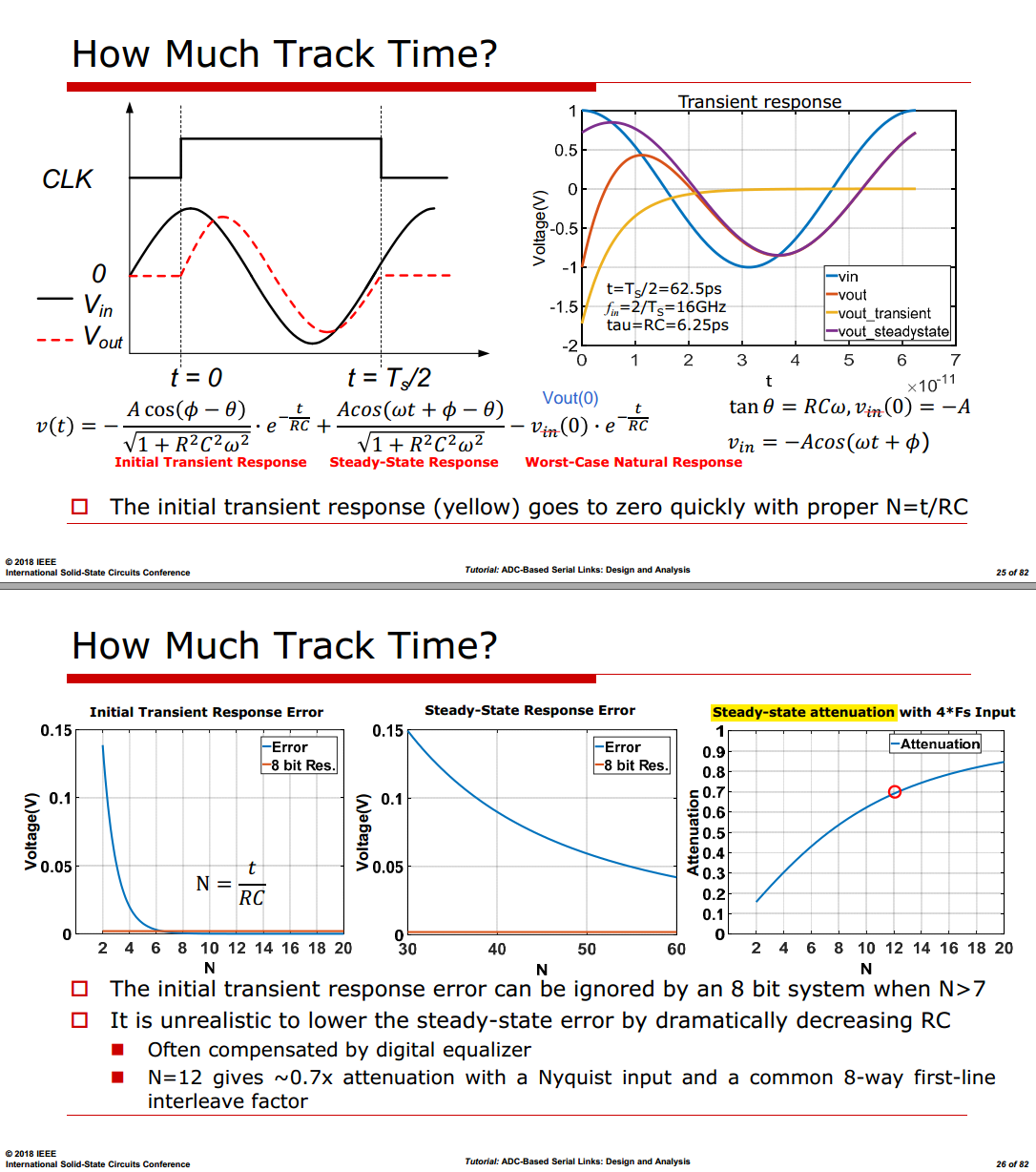
Finite Acquisition Time - Consider a sinusoidal input
utilizing Laplace transform pair
\[\begin{align} V_\text{in}(t)=\cos{\omega t+\theta} & \overset{\mathcal{L}}{\Rightarrow} \frac{s\cos \theta-\omega \sin \theta}{s^2+\omega^2} \\ h(t) & \overset{\mathcal{L}}{\Rightarrow} \frac{\frac{1}{\tau}}{s+\frac{1}{\tau}} \end{align}\]
Then,
\[\begin{align} V_\text{out}(s) &= V_\text{in}(s)\cdot H(s) \\ &= \frac{s\cos \theta-\omega \sin \theta}{s^2+\omega^2} \cdot \frac{\frac{1}{\tau}}{s+\frac{1}{\tau}} \\ &= \frac{A}{s+\frac{1}{\tau}} + \frac{Bs+C}{s^2+\omega^2} \end{align}\]
Obtain,
\[\begin{align} A &= -\frac{\cos(\theta - \phi)}{\sqrt{\tau ^2 \omega^2 +1}} \\ B & = -A \\ C &= -\frac{\omega \sin(\theta - \phi)}{\sqrt{\tau ^2 \omega^2 +1}} \end{align}\]
That is \[ V_\text{out}(s) = -\frac{\cos(\theta - \phi)}{\sqrt{\tau ^2 \omega^2 +1}} \frac{1}{s+\frac{1}{\tau}} + \frac{1}{\sqrt{\tau ^2 \omega^2 +1}}\frac{s\cos(\theta - \phi) - \omega \sin(\theta - phi)}{s^2+\omega^2} \]
where \(\phi = \arctan(\omega \tau)\)
Boris Murmann, EE315B VLSI Data Conversion Circuits, Autumn 2013 [pdf]
Redundancy
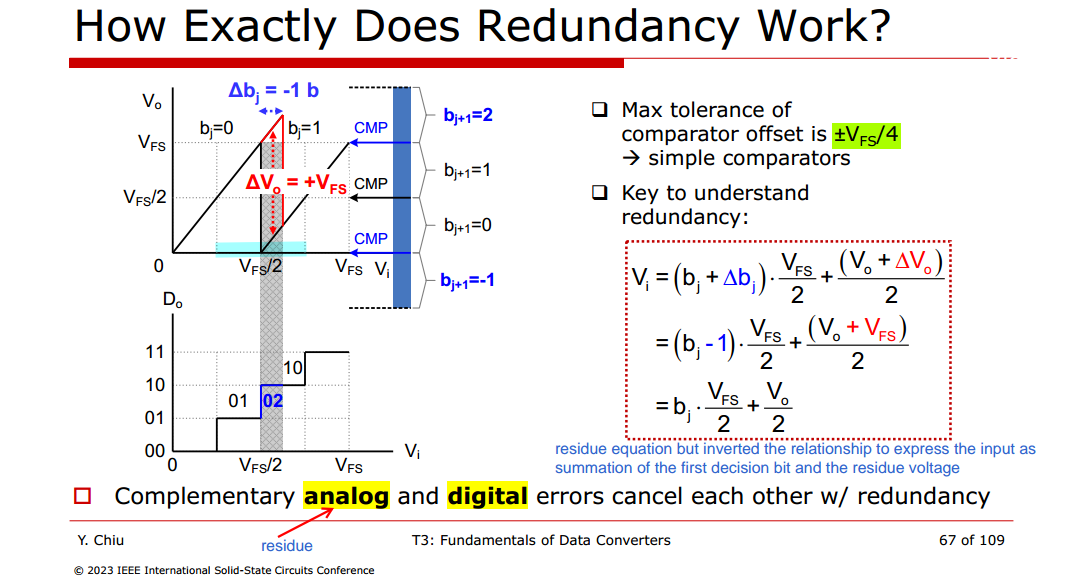
Max tolerance of comparator offset is \(\pm V_{FS}/4\)
- \(b_j\) error is \(\pm 1\)
- \(b_{j+1}\) error is \(\pm 2\) , wherein \(b_{j+1}\): \(0\to 2\) or \(1\to -1\)
i.e. complementary analog and digital errors cancel each other, \(V_o +\Delta V_{o}\) should be in over-/under-range comparators (\(-V_{FS}/2 \sim 3V_{FS}/2\))
\[\begin{align} V_{in,j} &= (b_j + \Delta b_j)\cdot \frac{V_{FS}}{2} + \frac{V_{out,j}+\Delta V_{out,j}}{2} \\ V_{in,{j+1}} &= (b_{j+1} + \Delta b_{j+1})\cdot \frac{V_{FS}}{2} + \frac{V_{out,j+1}+\Delta V_{out,j+1}}{2} \end{align}\]
with \(V_{in,j+1} = V_{out,j}+\Delta V_{out,j}\)
\[\begin{align} V_{in,j} &= (b_j + \Delta b_j)\cdot \frac{V_{FS}}{2} + \frac{1}{2} \left\{ (b_{j+1} + \Delta b_{j+1})\cdot \frac{V_{FS}}{2} + \frac{V_{out,j+1}+\Delta V_{out,j+1}}{2} \right\} \\ &= (b_j + \Delta b_j)\cdot \frac{V_{FS}}{2} + \frac{1}{2}(b_{j+1} + \Delta b_{j+1})\cdot \frac{V_{FS}}{2}+ \frac{1}{2}\frac{V_{in,j+2}}{2} \\ &=\tilde{b_j} \cdot \frac{V_{FS}}{2}+ \tilde{b_{j+1}}\cdot \frac{V_{FS}}{4}+ \frac{1}{4}V_{in,j+2} \end{align}\]
where \(b_j\) is 1-bit residue without redundancy and \(\tilde{b_j}\) is redundant bits
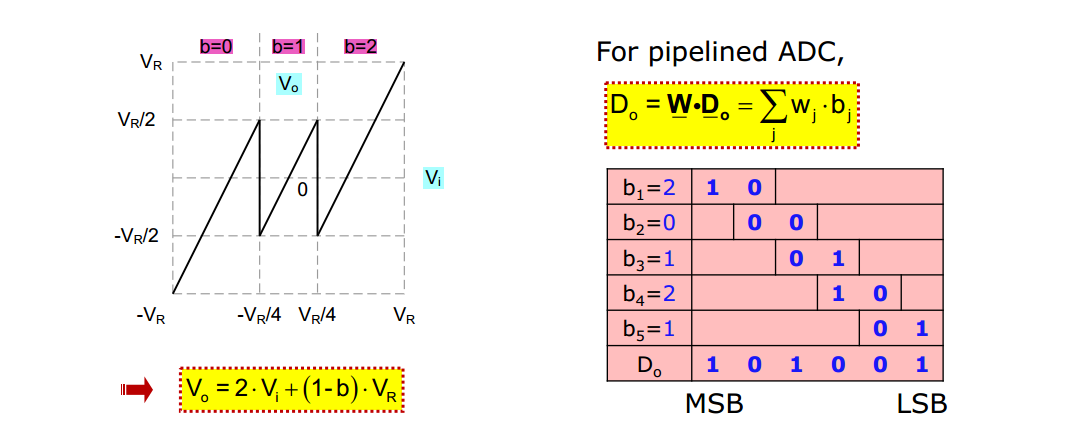
Uniform Sub-Radix-2 SAR ADC
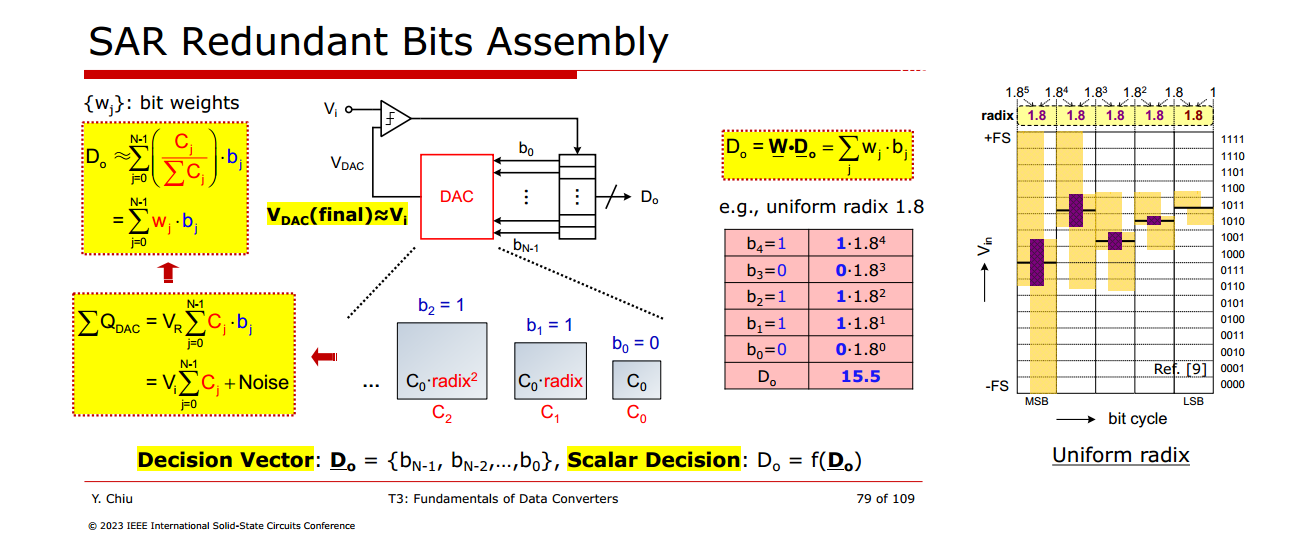
Minimal analog complexity, no additional decoding effort
Chang, Albert Hsu Ting. "Low-power high-performance SAR ADC with redundancy and digital background calibration." (2013). [https://dspace.mit.edu/bitstream/handle/1721.1/82177/861702792-MIT.pdf]
Kuttner, Franz. "A 1.2V 10b 20MSample/s non-binary successive approximation ADC in 0.13/spl mu/m CMOS." 2002 IEEE International Solid-State Circuits Conference. Digest of Technical Papers (Cat. No.02CH37315) 1 (2002): 176-177 vol.1. [https://sci-hub.se/10.1109/ISSCC.2002.992993]
T. Ogawa, H. Kobayashi, et. al., "SAR ADC Algorithm with Redundancy and Digital Error Correction." IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 93-A (2010): 415-423. [paper, slides]
B. Murmann, “On the use of redundancy in successive approximation A/D converters,” International Conference on Sampling Theory and Applications (SampTA), Bremen, Germany, July 2013. [https://www.eurasip.org/Proceedings/Ext/SampTA2013/papers/p556-murmann.pdf]
Krämer, M. et al. (2015) High-resolution SAR A/D converters with loop-embedded input buffer. dissertation. Available at: [http://purl.stanford.edu/fc450zc8031].
sarthak, "Visualising redundancy in a 1.5 bit pipeline ADC“ [https://electronics.stackexchange.com/a/523489/233816]
Testing
TODO 📅
Kent H. Lundberg "Analog-to-Digital Converter Testing" [https://www.mit.edu/~klund/A2Dtesting.pdf]
Tai-Haur Kuo, Da-Huei Lee "Analog IC Design: ADC Measurement" [http://msic.ee.ncku.edu.tw/course/aic/202309/ch13%20(20230111).pdf] [http://msic.ee.ncku.edu.tw/course/aic/aic.html]
ESE 6680: Mixed Signal Design and Modeling "Lec 20: April 10, 2023 Data Converter Testing" [https://www.seas.upenn.edu/~ese6680/spring2023/handouts/lec20.pdf]
Degang Chen. "Distortion Analysis" [https://class.ece.iastate.edu/djchen/ee435/2017/Lecture25.pdf]
ADC INL/DNL
TODO 📅
EndpointmethodBestFitmethod
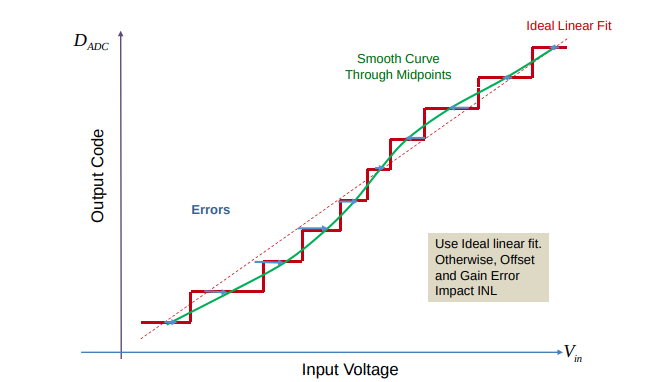
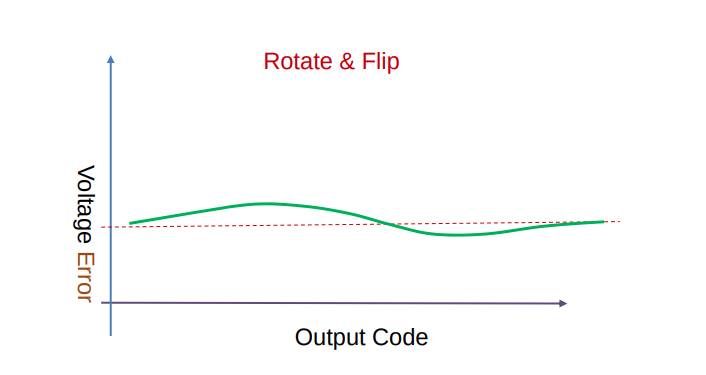
INL/DNL Measurements for High-Speed Analog-to Digital Converters (ADCs) [https://picture.iczhiku.com/resource/eetop/sYKTSqLfukeHSmMB.pdf]
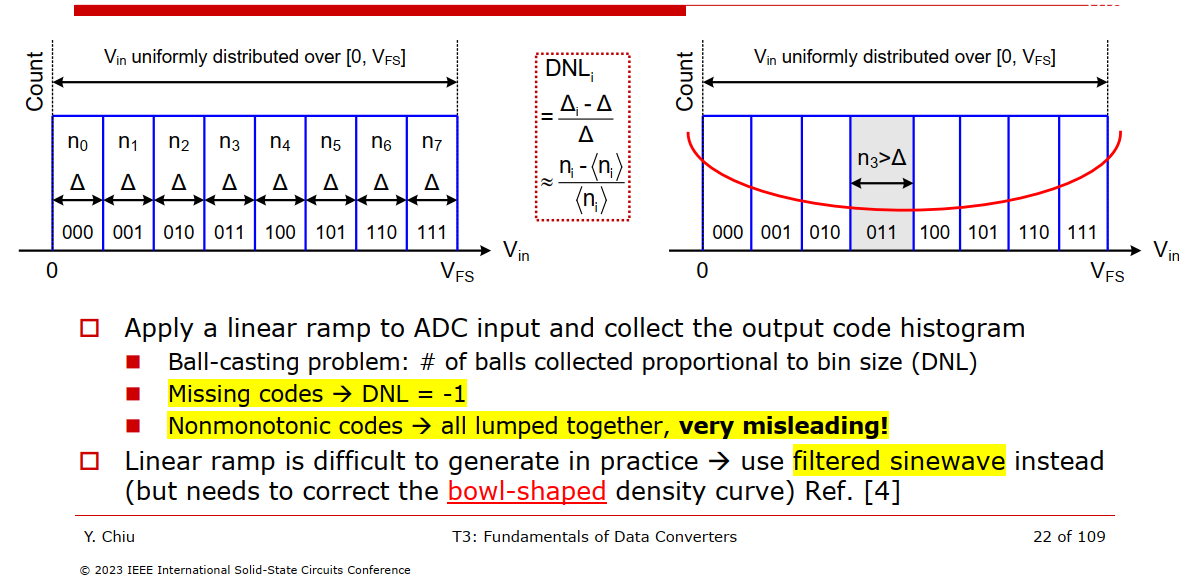
Code Density Test
Apply a linear ramp to ADC input
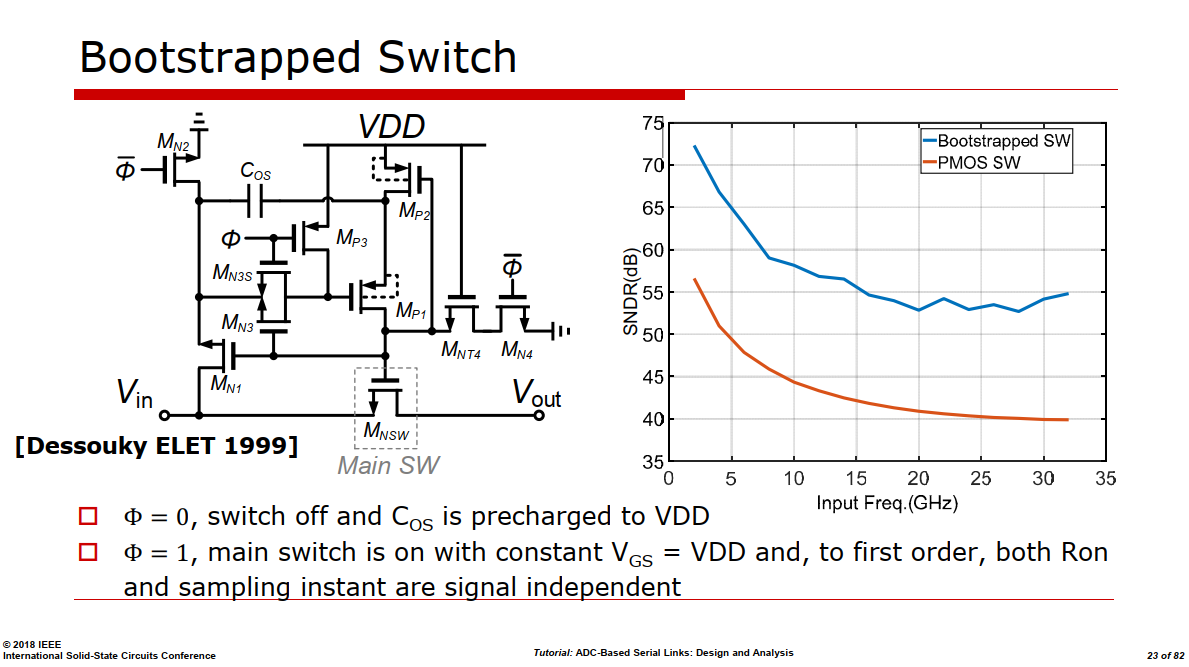
Bootstrapped Switch
A. Abo et al., "A 1.5-V, 10-bit, 14.3-MS/s CMOS Pipeline Analog-to Digital Converter," IEEE J. Solid-State Circuits, pp. 599, May 1999 [https://sci-hub.se/10.1109/4.760369]
Dessouky and Kaiser, "Input switch configuration suitable for rail-to-rail operation of switched opamp circuits," Electronics Letters, Jan. 1999. [https://sci-hub.se/10.1049/EL:19990028]
B. Razavi, "The Bootstrapped Switch [A Circuit for All Seasons]," in IEEE Solid-State Circuits Magazine, vol. 7, no. 3, pp. 12-15, Summer 2015 [https://www.seas.ucla.edu/brweb/papers/Journals/BRSummer15Switch.pdf]
B. Razavi, "The Design of a bootstrapped Sampling Circuit [The Analog Mind]," IEEE Solid-State Circuits Magazine, Volume. 13, Issue. 1, pp. 7-12, Summer 2021. [http://www.seas.ucla.edu/brweb/papers/Journals/BR_SSCM_1_2021.pdf]
Quantization Noise & its Spectrum
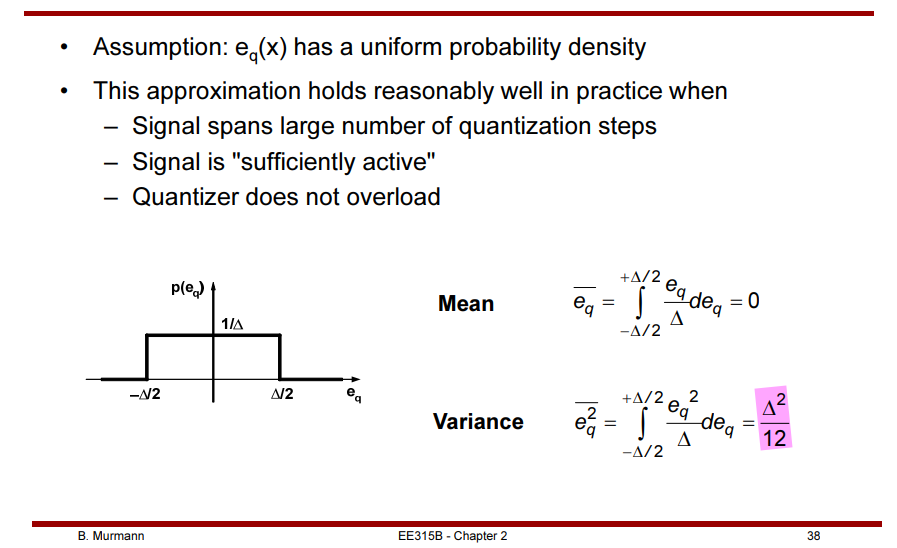
Quantization noise is less with higher resolution as the input range is divided into a greater number of smaller ranges
This error can be considered a quantization noise with RMS

Quantization is NOT Noise
N. Blachman, "The intermodulation and distortion due to quantization of sinusoids," in IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 33, no. 6, pp. 1417-1426, December 1985 [https://sci-hub.st/10.1109/TASSP.1985.1164729]
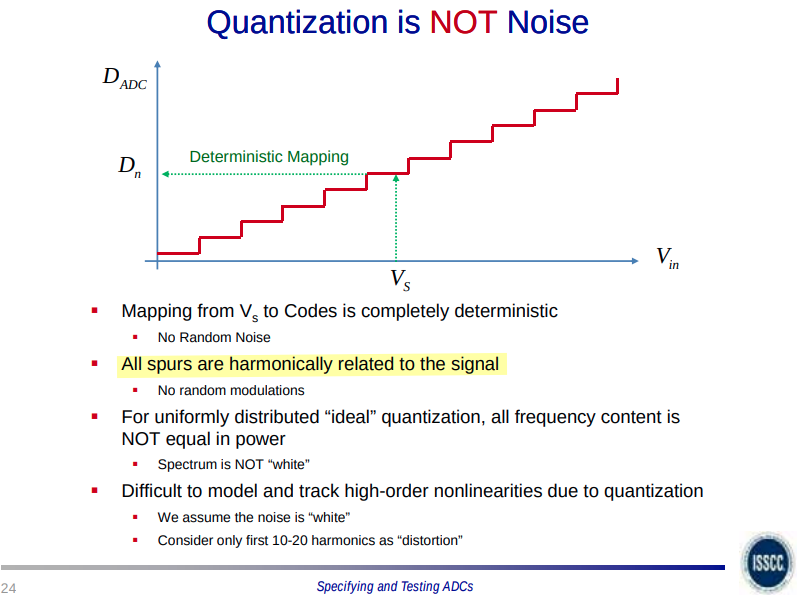
The quantization noise is an infinite sum of input signal odd harmonics, where the amplitude of the harmonics is determined by a sum of a Bessel function
"Quantization noise is white", because for a high number of bits, it looks white in the FFT

ENOB & SQNR
The quantization noise power \(P_Q\) for a uniform quantizer with step size \(\Delta\) is given by \[ P_Q = \frac{\Delta ^2}{12} \] For a full-scale sinusoidal input signal with an amplitude equal to \(V_{FS}/2\), the input signal is given by \(x(t) = \frac{V_{FS}}{2}\sin(\omega t)\)
Then input signal power \(P_s\) is \[ P_s = \frac{V_{FS}^2}{8} \] Therefore, the signal-to-quantization noise ratio (SQNR) is given by \[ \text{SQNR} = \frac{P_s}{P_Q} = \frac{V_{FS}^2/8}{\Delta^2/12}=\frac{V_{FS}^2/8}{V_{FS}^2/(12\times 2^{2N})} = \frac{3\times 2^{2N}}{2} \] where \(N\) is the number of quantization bits
When represented in dBs \[ \text{SQNR(dB)} = 10\log(\frac{P_s}{P_Q}) = 10\log(\frac{3\times 2^{2N}}{2})= 20N\log(2) + 10\log(\frac{3}{2})= 6.02N + 1.76 \]

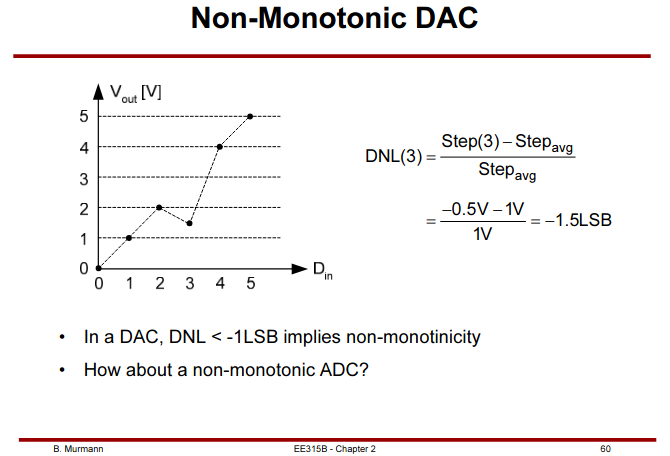
DAC DNL
One difference between ADC and DAC is that DAC DNL can be less than -1 LSB
In a DAC, DNL < -1LSB implies non-monotonicity
DAC INL
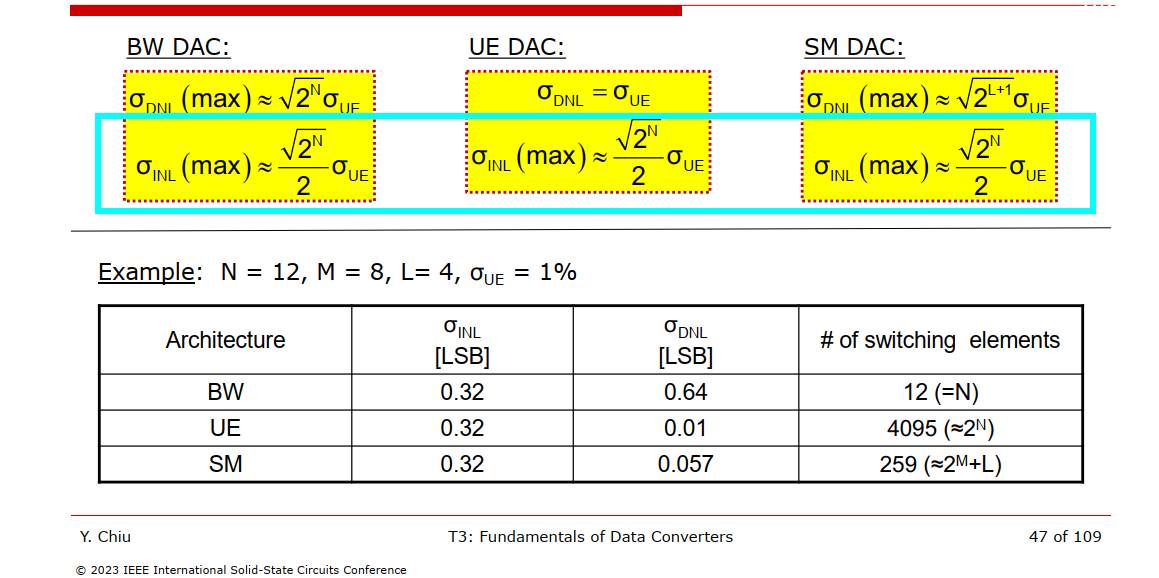
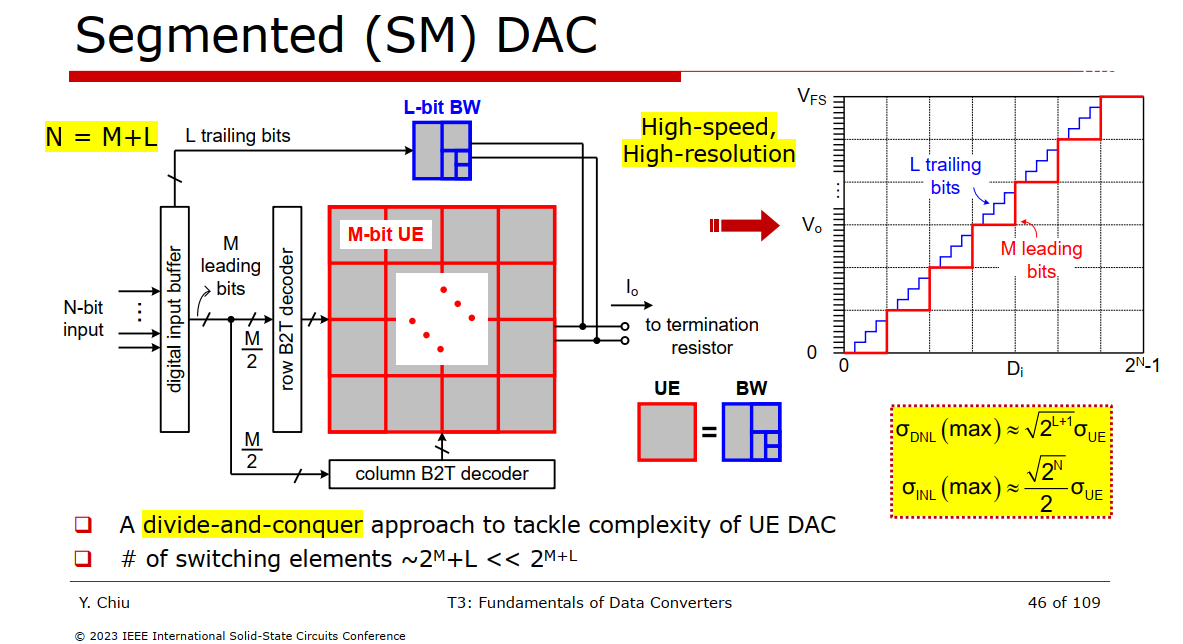
The worst INL of three DAC Architecture is same
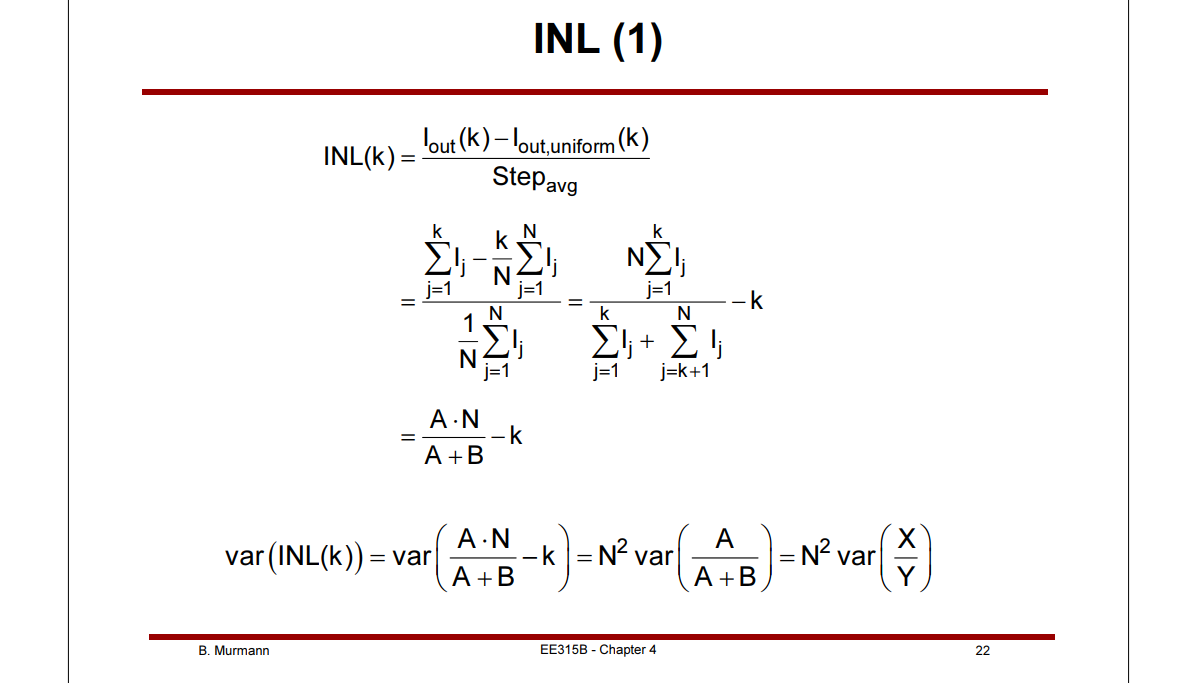
- \(A = \sum_{j=1}^k I_j\), \(B=\sum_{j=k+1}^N I_j\)
- A and B are independent with \(\sigma_A^2 = k\sigma_u^2\) and \(\sigma_B^2=(N-k)\sigma_u^2\)
Therefore \[ \mathrm{Var}\left(\frac{X}{Y}\right)\simeq \frac{k^2}{N^2}\left(\frac{\sigma_i^2}{kI_u^2} + \frac{\sigma_i^2}{NI_u^2} -2\frac{\mathrm{cov}(X,Y)}{kNI_u^2}\right) \] and \[\begin{align} \mathrm{cov}(X,Y) &= E[XY] - E[X]E[Y] = E[A(A+B)] - kNI_u^2 \\ &= E[A^2]+E[A]E[B] - kNI_u^2= \sigma_A^2+E[A]^2 + k(N-k)I_u^2 - kNI_u^2\\ &= k\sigma_i^2 + k^2I_u^2+ k(N-k)I_u^2 - kNI_u^2 \\ &= k\sigma_i^2 \end{align}\]
Finally, \[ \mathrm{Var}\left(\frac{X}{Y}\right)\simeq \frac{k^2}{N^2}\left(\frac{\sigma_i^2}{kI_u^2} + \frac{\sigma_i^2}{NI_u^2} -2\frac{k\sigma_i^2}{kNI_u^2}\right) = \frac{k^2}{N^2}\left(\frac{1}{k}- \frac{1}{N}\right)\sigma_u^2 \] i.e. \[ \mathrm{Var(INL(k))} = k^2\left(\frac{1}{k}- \frac{1}{N}\right)\sigma_u^2 = k\left(1- \frac{k}{N}\right)\sigma_u^2 \]
Standard deviation of INL is maximum at mid-scale (k=N/2)
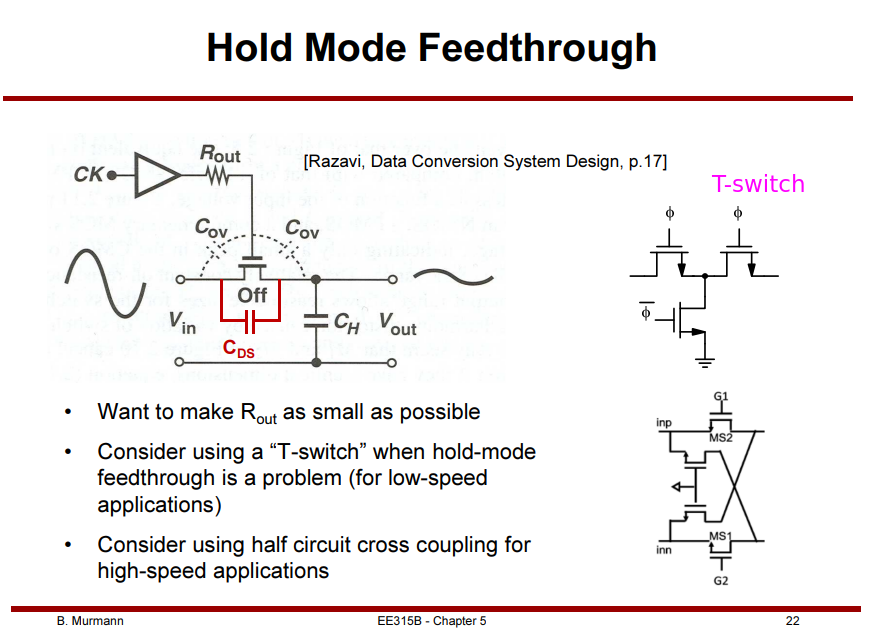
Hold Mode Feedthrough

P. Schvan et al., "A 24GS/s 6b ADC in 90nm CMOS," 2008 IEEE International Solid-State Circuits Conference - Digest of Technical Papers, San Francisco, CA, USA, 2008, pp. 544-634
B. Sedighi, A. T. Huynh and E. Skafidas, "A CMOS track-and-hold circuit with beyond 30 GHz input bandwidth," 2012 19th IEEE International Conference on Electronics, Circuits, and Systems (ICECS 2012), Seville, Spain, 2012, pp. 113-116
Tania Khanna, ESE 568: Mixed Signal Circuit Design and Modeling [https://www.seas.upenn.edu/~ese5680/fall2019/handouts/lec11.pdf]
Coherent Sampling
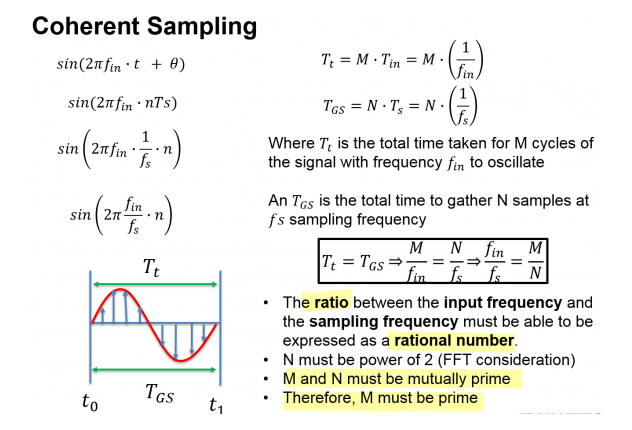
\[ \frac{f_{\text{in}}}{f_{\text{s}}}=\frac{M_C}{N_R} \]
\(f_\text{in}\) and \(f_s\) must be incommensurate (\(f_s/f_\text{in}\) is irrational number. btw, co-prime is sufficient but not necessary)
\(M_C\) and \(N_R\) must be co-prime
Samples must include integer # of cycles of input signal
An irreducible ratio ensures identical code sequences not to be repeated multiple times.
Given that \(\frac{M_C}{N_R}\) is irreducible, and \(N_R\) is a power of 2, an odd number for \(M_C\) will always produce an irreducible ratio
Assuming there is a common factor \(k\) between \(M_C\) and \(N_R\), i.e. \(\frac{M_C}{N_R}=\frac{k M_C'}{k N_R'}\)
The samples (\(n\in[1, N_R]\))
\[ y[n] = \sin\left( \omega_{\text{in}} \cdot t_n \right) = \sin\left( \omega_{\text{in}} \cdot n\frac{1}{f_s} \right) = \sin\left( \omega_{\text{in}} \cdot n\frac{1}{f_{\text{in}}}\frac{M_C}{N_R} \right) = \sin\left( 2\pi n\frac{M_C}{N_R} \right) \]
Then
\[ y[n+N_R'] = \sin\left( 2\pi (n+N_R')\frac{M_C}{N_R} \right) = \sin\left( 2\pi n \frac{M_C}{N_R} + 2\pi N_R'\frac{M_C}{N_R}\right) = \sin\left( 2\pi n \frac{M_C}{N_R} + 2\pi N_R'\frac{kM_C'}{kN_R'} \right) = \sin\left( 2\pi n \frac{M_C}{N_R}\right) \]
So, the samples is repeated \(y[n] = y[n+N_R']\)
\(N_R\) & \(M_C\) irreducible ratio (mutually prime)
- Periodic sampling points result in periodic quantization errors
- Periodic quantization errors result in harmonic distortion
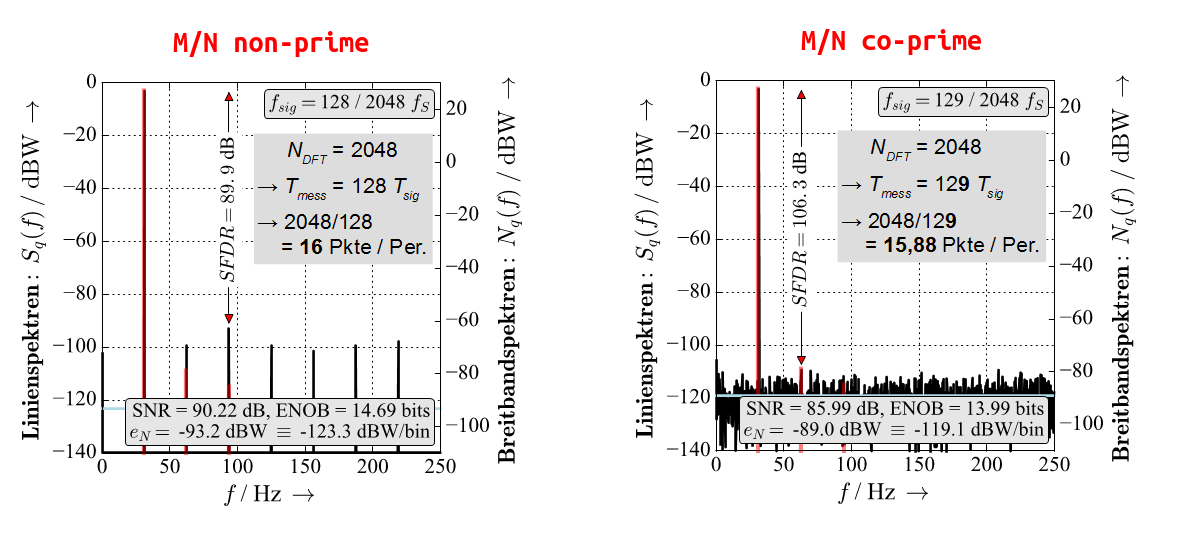
Choosing M/N non-prime repeats the signal quantization periodically and fewer quantization steps are measured. The quantization repeats periodically and creates a line spectrum that can obscure real frequency lines (e.g. the red lines in the images below, created by non-linearities of the ADC).
[https://www.dsprelated.com/thread/469/coherent-sampling-very-brief-and-simple]
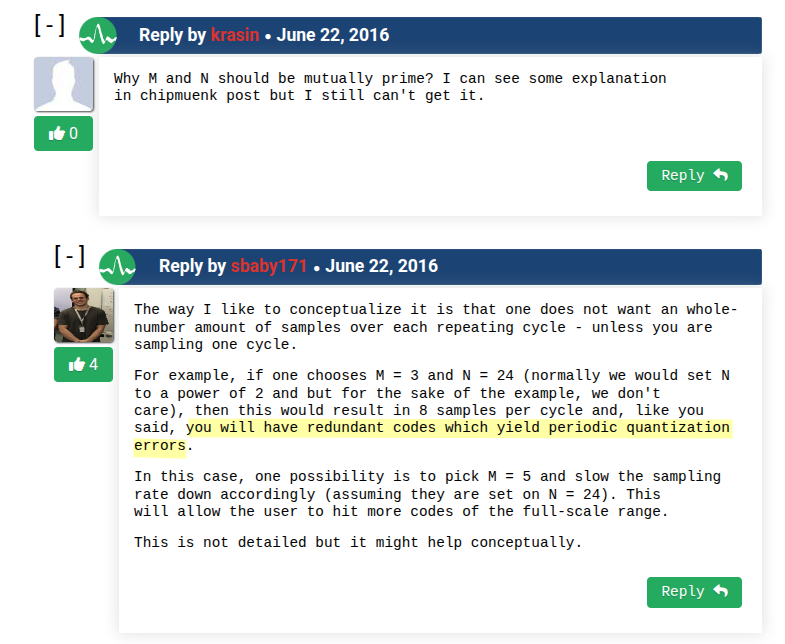

Thermometer to Binary encoder
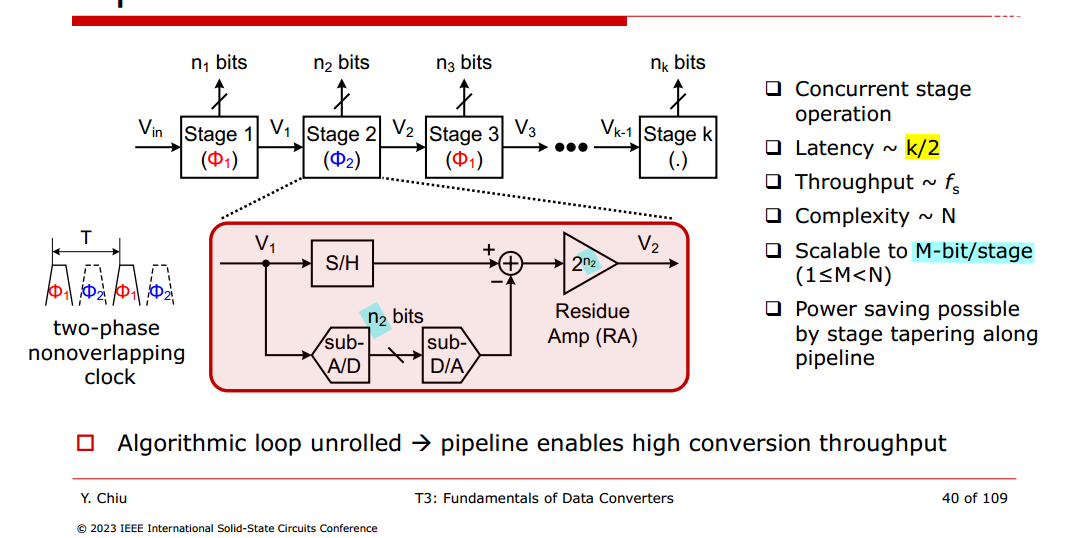
Pipeline ADC
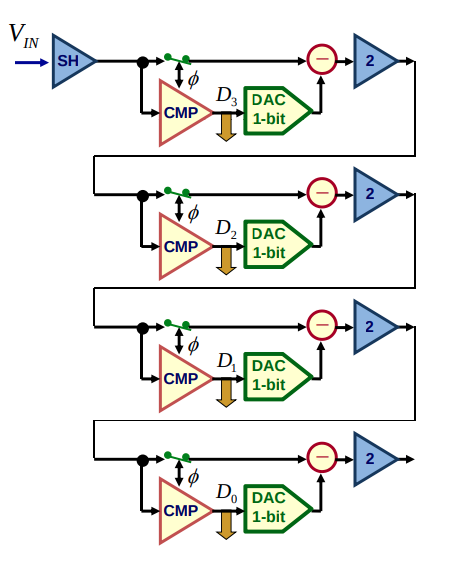
CMP reference voltage is 0.5vref, DAC output is 0.5vref or 0
residual error \[ V_{r,n} = (V_{r,n-1}-\frac{1}{2}b_{n})\cdot 2 \] and \(V_{r,-1}=V_i\) \[ V_{r,n-1} = 2^{n}V_i -\sum_{k=0}^{n-1}2^{n-k-1}b_k = 2^{n}\left(V_i - \sum_{k=0}^{n-1}\frac{b_k}{2^{k+1}}\right) \]
here, \(b_0\) is first stage and MSB
It divides the process into several comparison stages, the number of which is proportional to the number of bits
Due to the pipeline structure of both analog and digital signal path, inter-stage residue amplification is needed which consumes considerable power and limits high speed operation
Vishal Saxena, "Pipelined ADC Design - A Tutorial"[https://www.eecis.udel.edu/~vsaxena/courses/ece517/s17/Lecture%20Notes/Pipelined%20ADC%20NonIdealities%20Slides%20v1_0.pdf] [https://www.eecis.udel.edu/~vsaxena/courses/ece517/s17/Lecture%20Notes/Pipelined%20ADC%20Slides%20v1_2.pdf]
Bibhu Datta Sahoo, Analog-to-Digital Converter Design From System Architecture to Transistor-level [http://smdpc2sd.gov.in/downloads/IGF/IGF%201/Analog%20to%20Digital%20Converter%20Design.pdf]
Bibhu Datta Sahoo, Associate Professor, IIT, Kharagpur, [https://youtu.be/HiIWEBAYRJY?si=pjQnIdi03i5N7805]
R-2R & C-2C
TODO 📅
Conceptually, area goes up linearly with number of bit slices
drawback of the R-2R DAC
\(N_b\) bit binary + \(N_t\) bit thermometer DAC
\(N_b\) bit binary can be simplified with Thevenin Equivalent \[ V_B = \sum_{n=0}^{N_b-1} \frac{B_n}{2^{N_b-n}} \] with thermometer code
\[\begin{align} V_o &= V_B\frac{\frac{2R}{2^{N_t}-1}}{\frac{2R}{2^{N_t}-1}+ 2R}+\sum_{n=0}^{2^{N_t}-2}T_n\frac{\frac{2R}{2^{N_t}-1}}{\frac{2R}{2^{N_t}-1}+ 2R} \\ &= \frac{V_B}{2^{N_t}} + \frac{\sum_{n=0}^{2^{N_t}-2}T_n}{2^{N_t}} \\ &= \sum_{n=0}^{N_b-1} \frac{B_n}{2^{N_t+N_b-n}} + \frac{\sum_{n=0}^{2^{N_t}-2}T_n}{2^{N_t}} \end{align}\]
B. Razavi, "The R-2R and C-2C Ladders [A Circuit for All Seasons]," in IEEE Solid-State Circuits Magazine, vol. 11, no. 3, pp. 10-15, Summer 2019 [https://www.seas.ucla.edu/brweb/papers/Journals/BR_SSCM_3_2019.pdf]
4bit binary R2R DAC with Ru=1kOhm
RVB equivalent R
Binary-Weighted (BW) DAC
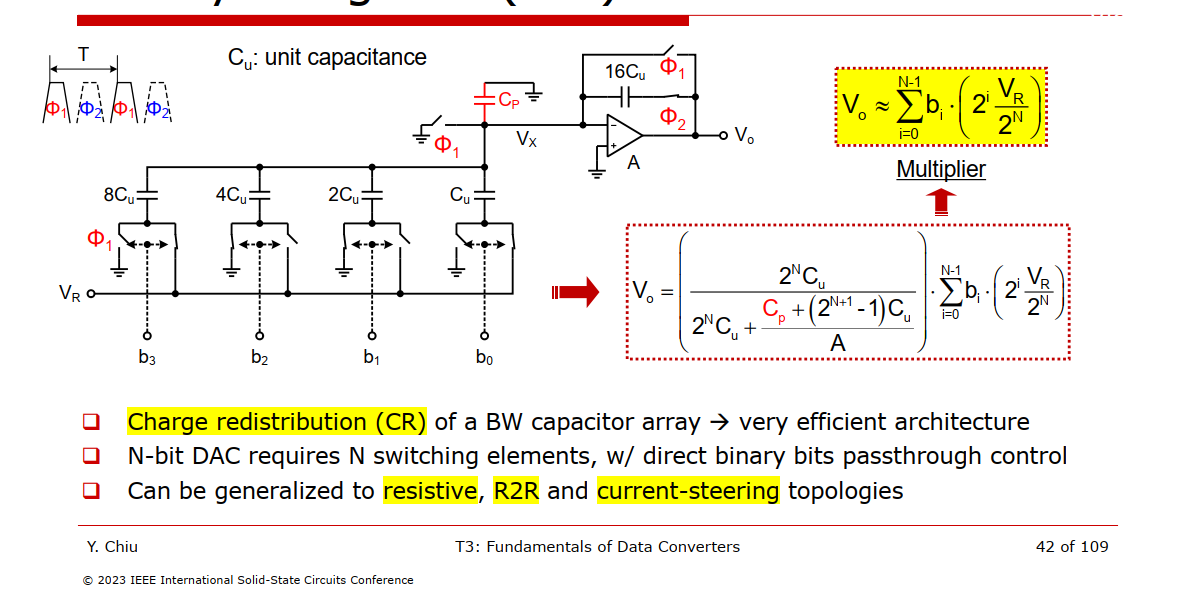
During \(\Phi_1\), all capacitor are shorted, the net charge at \(V_x\) is 0
During \(\Phi_2\), the charge at bottom plate of CDAC \[ Q_{DAC,btm} = \sum_{i=0}^{N-1}(b_i\cdot V_R - V_x)\cdot 2^{i}C_u = C_uV_R\sum_{i=0}^{N-1}b_i2^i - (2^N-1)C_uV_x \] the charge at the internal plate of integrator \[ Q_{intg} = V_x C_p + (V_x - V_o)2^NC_u \] and we know \(-V_x A = V_o\) and \(Q_{DAC,btm} = Q_{intg}\) \[ C_uV_R\sum_{i=0}^{N-1}b_i2^i - (2^N-1)C_uV_x = V_x C_p + (V_x - V_o)2^NC_u \] i.e. \[ C_uV_R\sum_{i=0}^{N-1}b_i2^i = (2^N-1)C_uV_x + V_x C_p + (V_x - V_o)2^NC_u \] therefore \[ -V_o = \frac{2^N C_u}{\frac{(2^{N+1}-1)C_u+C_p}{A}+2^NC_u}\sum_{i=0}^{N-1}b_i\left(2^i\frac{V_R}{2^N}\right)\approx \sum_{i=0}^{N-1}b_i\left(2^i\frac{V_R}{2^N}\right) \]
Midscale (MSB Transition) often is the largest DNL error
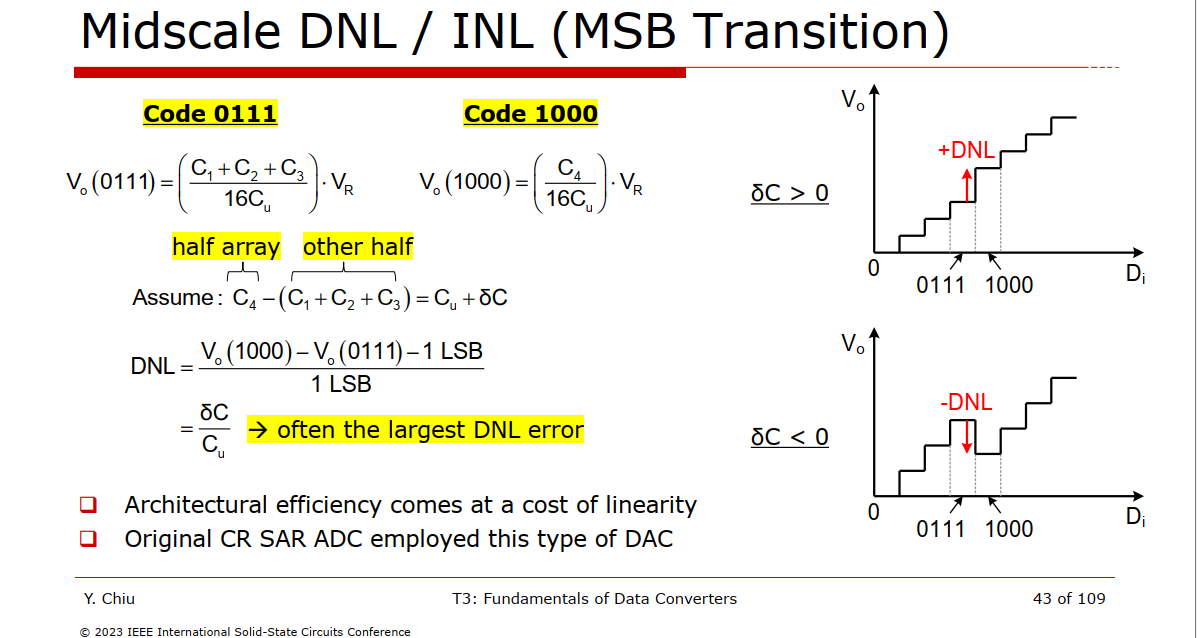
\(C_4\) and \(C_1+C_2+C_3\) are independent (can't cancel out) and their variance is two largest (\(16\sigma_u^2\), \(15\sigma_u^2\), ), the total standard deviation is \(\sqrt{16\sigma_u^2+15\sigma_u^2}=\sqrt{31}\sigma_u\)
INL, DNL of current steering DAC
MOS mismatch
Current mirror mismatch analysis
INL/DNL analysis of current steering DAC
reference
Maloberti, F. Data Converters. Dordrecht, Netherlands: Springer, 2007.
Ahmed M. A. Ali 2016, "High Speed Data Converters" [pdf]
Razavi B. Analysis and Design of Data Converters. Cambridge University Press; 2025.
Aaron Buchwald, ISSCC2010 T1: "Specifying & Testing ADCs" [https://www.nishanchettri.com/isscc-slides/2010%20ISSCC/Tutorials/T1.pdf]
Ahmed M. A. Ali. CICC 2018: High Speed Pipelined ADCs: Fundamentals and Variants [https://picture.iczhiku.com/resource/eetop/SyIGzGRYsHFehcnX.pdf]
John P. Keane, ISSCC2020 T5: "Fundamentals of Time-Interleaved ADCs" [https://www.nishanchettri.com/isscc-slides/2020%20ISSCC/TUTORIALS/T5Visuals.pdf]
Yun Chiu, ISSCC2023 T3: "Fundamentals of Data Converters" [https://www.nishanchettri.com/isscc-slides/2023%20ISSCC/TUTORIALS/T3.pdf]
—, "Design and Calibration Techniques for SAR and Pipeline ADCs" [http://formation-old.in2p3.fr/microelectronique15/IN2P3_ADC.pdf]
—, Radiation-Tolerant SAR ADC Architecture and Digital Calibration Techniques [https://indico.cern.ch/event/385097/attachments/768706/1054353/CERN_May15.pdf]
—, Recent Advances in Multistep Nyquist ADC's [https://www.eecis.udel.edu/~vsaxena/courses/ece614/Handouts/Recent%20Advances%20in%20Nyquist%20rate%20ADCs.pdf]
Boris Murmann, ISSCC2022 SC1: Introduction to ADCs/DACs: Metrics, Topologies, Trade Space, and Applications [https://www.nishanchettri.com/isscc-slides/2022%20ISSCC/SHORT%20COURSE/SC1.pdf]
—, ISSCC2012 SC3: Introduction to ADCs/DACs: Metrics, Topologies, Trade Space, and Applications [https://www.nishanchettri.com/isscc-slides/2012%20ISSCC/SHORT%20COURSE/SC3Visuals.pdf]
—, A/D Converter Figures of Merit and Performance Trends [https://www.nishanchettri.com/isscc-slides/2015%20ISSCC/CIRCUIT%20INSIGHTS/Murmann.pdf]
Aaron Buchwald, ISSCC 2008 T2 Pipelined A/D Converters: The Basics [pdf]
Yohan Frans, CICC2019 ES3-3- "ADC-based Wireline Transceivers" [pdf]
Samuel Palermo, ISSCC 2018 T10: ADC-Based Serial Links: Design and Analysis [https://www.nishanchettri.com/isscc-slides/2018%20ISSCC/TUTORIALS/T10/T10Visuals.pdf]
Ahmed M. A. Ali. ISSCC2021 T5: Calibration Techniques in ADCs [https://www.nishanchettri.com/isscc-slides/2021%20ISSCC/TUTORIALS/ISSCC2021-T5.pdf]
Jan Mulder Broadcom. ISSCC2015 T5: High-Speed Current-Steering DACs [https://www.nishanchettri.com/isscc-slides/2015%20ISSCC/TUTORIALS/ISSCC2015Visuals-T5.pdf]
M. Gu, Y. Tao, Y. Zhong, L. Jie and N. Sun, "Timing-Skew Calibration Techniques in Time-Interleaved ADCs," in IEEE Open Journal of the Solid-State Circuits Society [https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=10804623]
everynanocounts. Memos on FFT With Windowing. URL: https://a2d2ic.wordpress.com/2018/02/01/memos-on-fft-with-windowing/
How to choose FFT depth for ADC performance analysis (SINAD, ENOB). URL:https://dsp.stackexchange.com/a/38201
Computation of Effective Number of Bits, Signal to Noise Ratio, & Signal to Noise & Distortion Ratio Using FFT. URL:https://cdn.teledynelecroy.com/files/appnotes/computation_of_effective_no_bits.pdf
Kester, Walt. (2009). Understand SINAD, ENOB, SNR, THD, THD + N, and SFDR so You Don't Get Lost in the Noise Floor. URL:https://www.analog.com/media/en/training-seminars/tutorials/MT-003.pdf
T. C. Hofner: Dynamic ADC testing part I. Defining and testing dynamic ADC parameters, Microwaves & RF, 2000, vol. 39, no. 11, pp. 75-84,162
T. C. Hofner: Dynamic ADC testing part 2. Measuring and evaluating dynamic line parameters, Microwaves & RF, 2000, vol. 39, no. 13, pp. 78-94
AN9675: A Tutorial in Coherent and Windowed Sampling with A/D Converters https://www.renesas.com/us/en/document/apn/an9675-tutorial-coherent-and-windowed-sampling-ad-converters
APPLICATION NOTE 3190: Coherent Sampling Calculator (CSC) https://www.stg-maximintegrated.com/en/design/technical-documents/app-notes/3/3190.html
Coherent Sampling (Very Brief and Simple) https://www.dsprelated.com/thread/469/coherent-sampling-very-brief-and-simple
Signal Chain Basics #160: Making sense of coherent and noncoherent sampling in data-converter testing https://www.planetanalog.com/signal-chain-basics-160-making-sense-of-coherent-and-noncoherent-sampling-in-data-converter-testing/
Signal Chain Basics #104: Understanding noise in ADCs https://www.planetanalog.com/signal-chain-basics-part-104-understanding-noise-in-adcs/
Signal Chain Basics #101: ENOB Degradation Analysis Over Frequency Due to Jitter https://www.planetanalog.com/signal-chain-basics-part-101-enob-degradation-analysis-over-frequency-due-to-jitter/
Clock jitter analyzed in the time domain, Part 1, Texas Instruments Analog Applications Journal (slyt379), Aug 2010 https://www.ti.com/lit/an/slyt379/slyt379.pdf
Clock jitter analyzed in the time domain, Part 2 https://www.ti.com/lit/slyt389
Measurement of Total Harmonic Distortion and Its Related Parameters using Multi-Instrument [pdf]
Application Note AN-4: Understanding Data Converters' Frequency Domain Specifications [pdf]
Belleman, J. (2008). From analog to digital. 10.5170/CERN-2008-003.131. [pdf]
HandWiki. Coherent sampling [link]
Luis Chioye, TI. Leverage coherent sampling and FFT windows when evaluating SAR ADCs (Part 1) [link]
Coherent Sampling vs. Window Sampling | Analog Devices https://www.analog.com/en/technical-articles/coherent-sampling-vs-window-sampling.html
Understanding Effective Number of Bits https://robustcircuitdesign.com/signal-chain-explorer/understanding-effective-number-of-bits/
ADC Input Noise: The Good, The Bad, and The Ugly. Is No Noise Good Noise? [https://www.analog.com/en/resources/analog-dialogue/articles/adc-input-noise.html]
Walt Kester, Taking the Mystery out of the Infamous Formula, "SNR = 6.02N + 1.76dB," and Why You Should Care [https://www.analog.com/media/en/training-seminars/tutorials/MT-001.pdf]
Dan Boschen, "How to choose FFT depth for ADC performance analysis (SINAD, ENOB)", [https://dsp.stackexchange.com/a/38201]
B. Razavi, "A Tale of Two ADCs - Pipelined Versus SAR" IEEE Solid-State Circuits Magazine, Volume. 7, Issue. 30, pp. 38-46, Summer 2015 [https://www.seas.ucla.edu/brweb/papers/Journals/BRSummer15ADC.pdf)]
Dr. Tai-Haur Kuo (郭泰豪 教授) Analog IC Design (類比積體電路設計) [http://msic.ee.ncku.edu.tw/course/aic/aic.html]
Converter Passion for data-converter professionals sharing thoughts on ADCs and DACs [https://converterpassion.wordpress.com/]
Boris Murmann, EE315B VLSI Data Conversion Circuits, Autumn 2013 [pdf]
MPScholar Analog-to-Digital Converters (ADCs) [https://www.monolithicpower.com/en/learning/mpscholar/analog-to-digital-converters]
tomverbeure. List of Analog Devices Tutorials [https://tomverbeure.github.io/2021/02/15/Analog-Devices-Tutorials.html]
