SAR ADC
Reference Ripple
C-H Chan (U. of Macau) "Extreme SAR ADCs - Exploring New Frontiers" Online Course (2024) : Reference Buffer in SAR ADC [https://youtu.be/vj98B7AaC9E]
C. Li, C. -H. Chan, Y. Zhu and R. P. Martins, "Analysis of Reference Error in High-Speed SAR ADCs With Capacitive DAC," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 66, no. 1, pp. 82-93, Jan. 2019 [https://ime.um.edu.mo/wp-content/uploads/magazines/961546494e705f6fd16b9f785a121030.pdf]
J. Zhong, Y. Zhu, S. -W. Sin, S. -P. U and R. P. Martins, "Thermal and Reference Noise Analysis of Time-Interleaving SAR and Partial-Interleaving Pipelined-SAR ADCs," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 62, no. 9, pp. 2196-2206, Sept. 2015 [https://sci-hub.st/10.1109/TCSI.2015.2452331]
C. -H. Chan et al., "60-dB SNDR 100-MS/s SAR ADCs With Threshold Reconfigurable Reference Error Calibration," in IEEE Journal of Solid-State Circuits, vol. 52, no. 10, pp. 2576-2588, Oct. 2017 [https://ime.um.edu.mo/wp-content/uploads/magazines/407e580ac0218605bcf9b9bbd0ea1109.pdf]
TODO 📅
Sampling Front-End (SFE) Pulse Response
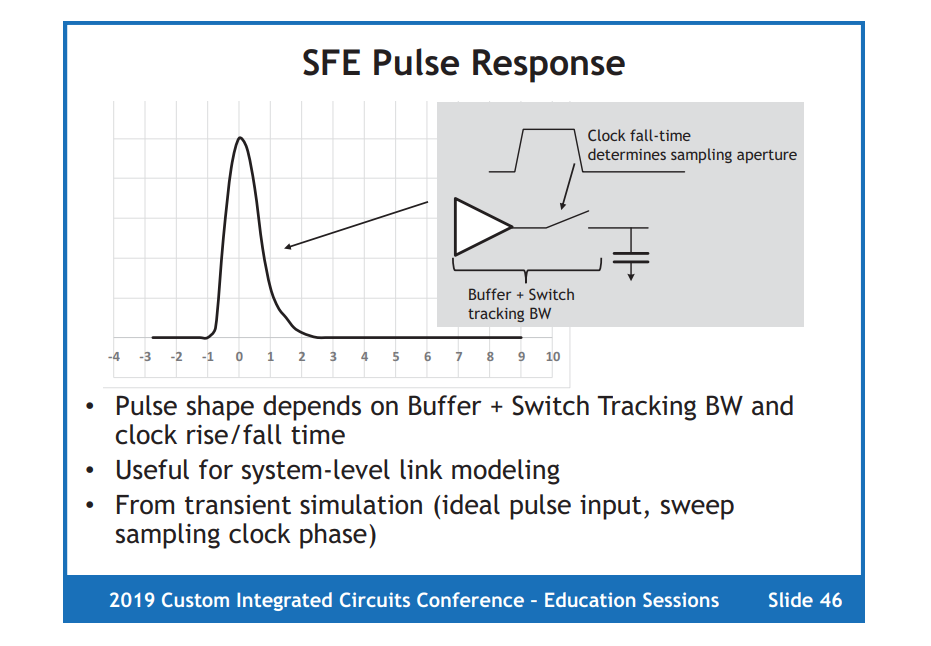
sweep the setup time between ideal pulse input and clock, sample the output of SFE at falling edge
sample-by-sample
3rd harmonic
bit-by-bit
The amplitude of the reference ripple is code-dependent as it is correlated with switching energy in each bit cycling
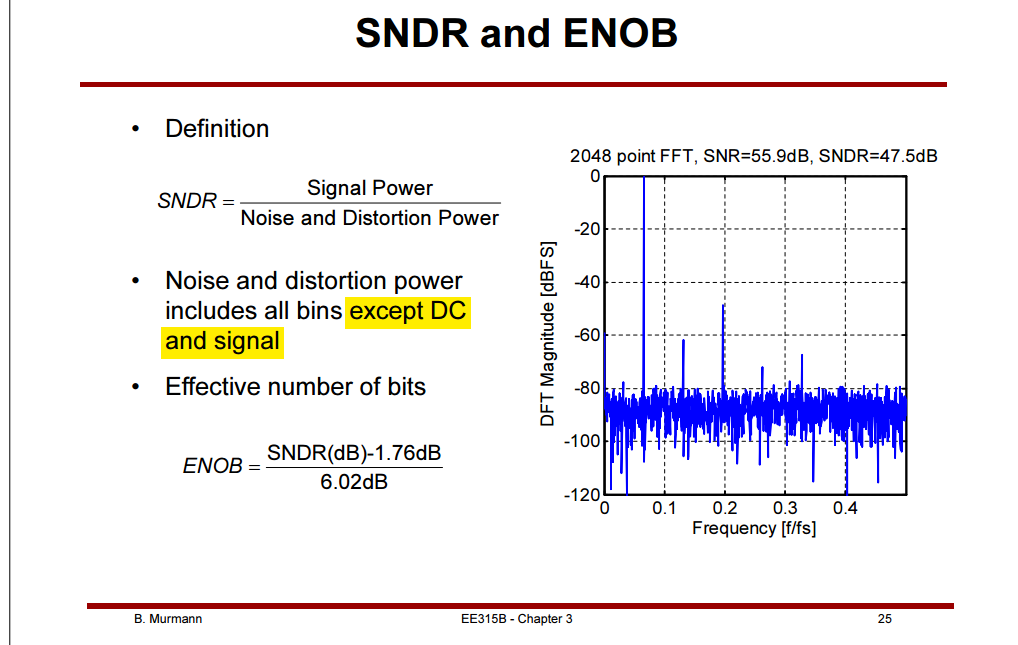
quantization error & quantization noise

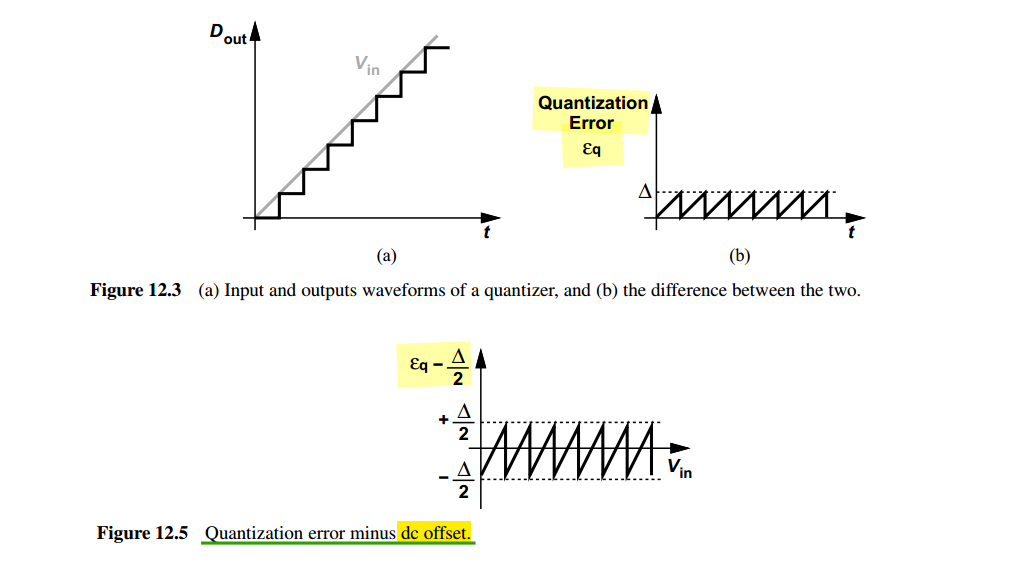

Notice \(e_q\in (0, \Delta)\) and its average is \(\Delta/2\). To calculate SNDR, DC component shall be excluded
Don't confuse resolution \(\Delta\) with Bounded Quantization Noise \(-\Delta/2 \sim \Delta/2\)
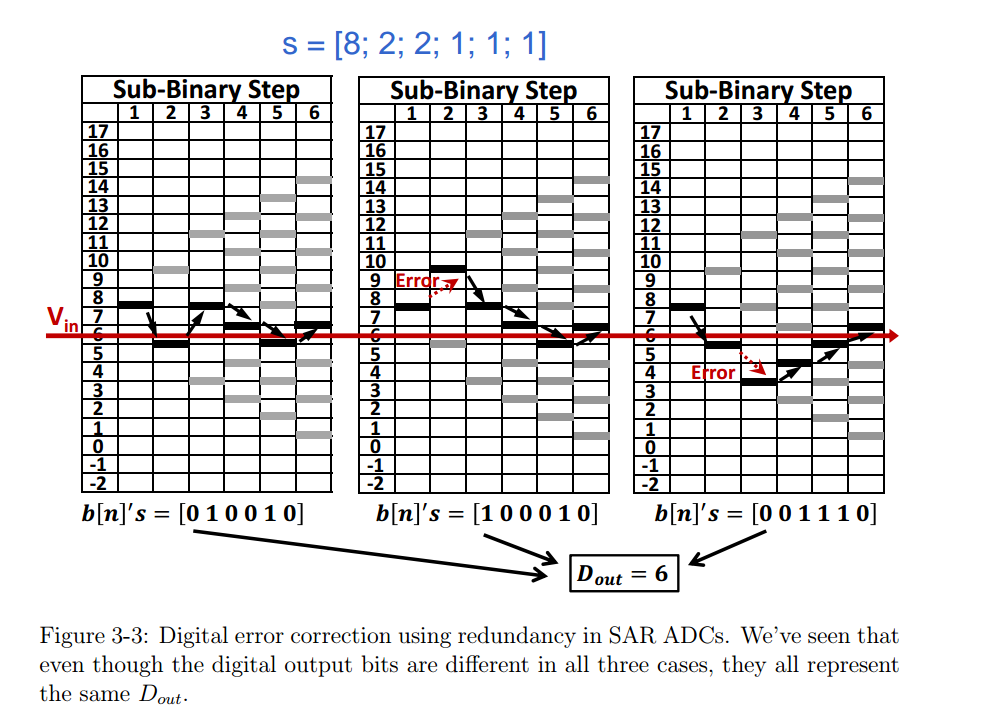
Redundancy
decision level
final digital output for an \(N\)-bit \(M\)-step ADC can be calculated \[ D_{out} = s(M) + \sum_{i=1}^{M-1}(2\cdot b[i] - 1)\times s(i) + (b[0] -1)\cdot s(1) \]
| i | M | M-1 | M-2 | ... | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|
| b[i] | b[M-1] | b[M-2] | ... | b[2] | b[1] | b[0] | |
| s[i] | s(M) | s(M-1) | s(M-2) | ... | s(2) | s(1) |
track the decision level
For \(N\)-bit binary weighted algorithm,\(N=M\) and \(s(i)=2^{i-1}\), where \(i\in \{N, N-1,...,2,1 \}\)
\[\begin{align} D_{out} &= s(M) + \sum_{i=1}^{M-1}(2\cdot b[i] - 1)\times s(i) + (b[0] -1) \\ &= 2^{N-1} + \sum_{i=1}^{N-1}2^i\cdot b[i] - \sum_{i=0}^{N-2}2^{i} + (b[0] -1) \\ &= \sum_{i=0}^{N-1} b[i] \cdot 2^i \end{align}\]
alternative method for d2a & CDAC equivalent weight
| i | M-1 | M-2 | ... | 2 | 1 | 0 |
|---|---|---|---|---|---|---|
| b[i] | b[M-1] | b[M-2] | ... | b[2] | b[1] | b[0] |
| w[i] | w[M-2] | ... | w[2] | w[1] | w[0] | |
| W[i] | 2w[M-2] | 2w[M-3] | ... | 2w[1] | 2w[0] | w[0] |
\[\begin{align} D_{out} &= \sum_{i=1}^{M-1}(2b_i -1)w_{i-1} + (b_0-1)w_0 \\ &= \sum_{i=1}^{M-1}b_i\cdot 2w_{i-1} + b_0\cdot w_0 -\sum_{i=1}^{M-1}w_{i-1} -w_0 \\ &= \left[\sum_{i=1}^{M-1}b_i\cdot 2w_{i-1} + b_0\cdot w_0\right] - \frac{1}{2}\left[\sum_{i=1}^{M-1}2w_{i-1} +w_0 + w_0\right] \\ &= \sum_{i=0}^{M-1}b_i\cdot W_i - \frac{1}{2}\left[\sum_{i=0}^{M-1}W_i + W_0\right] \end{align}\]
where \(W_i = 2w_{i-1}\) for \(i\in [M-1,1]\) and \(W_0 = w_0\)
Error Tolerance Window
\[ \varepsilon_t(n) = \sum_{i=1}^{n-2} s(i) - s(n-1) \]
where \(n\in [1, N]\), and \(N\)-bit SAR
For the \(n\)th output bit, once a decision is made, the next decision level will either move up or down by the step size of \(s(n − 1)\)
If this decision is erroneous, then the sum of the follow-on step sizes, \(s(n − 2)\), \(s(n − 3)\), ..., \(s(1)\), must be large enough and exceed the value of the current step size to counteract this mistake
The exceeded amount is the tolerance window for that decision level
sub-binary search


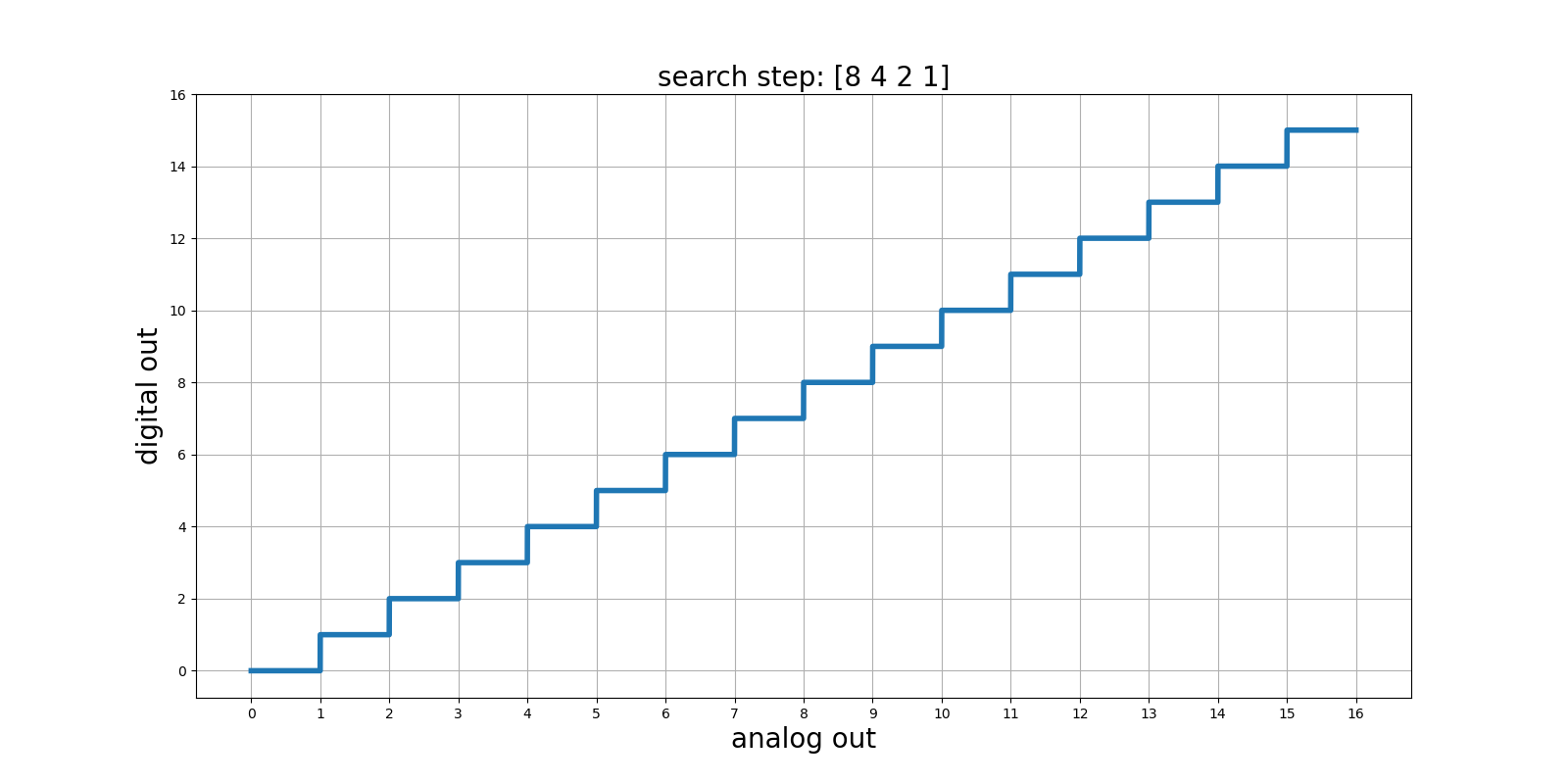
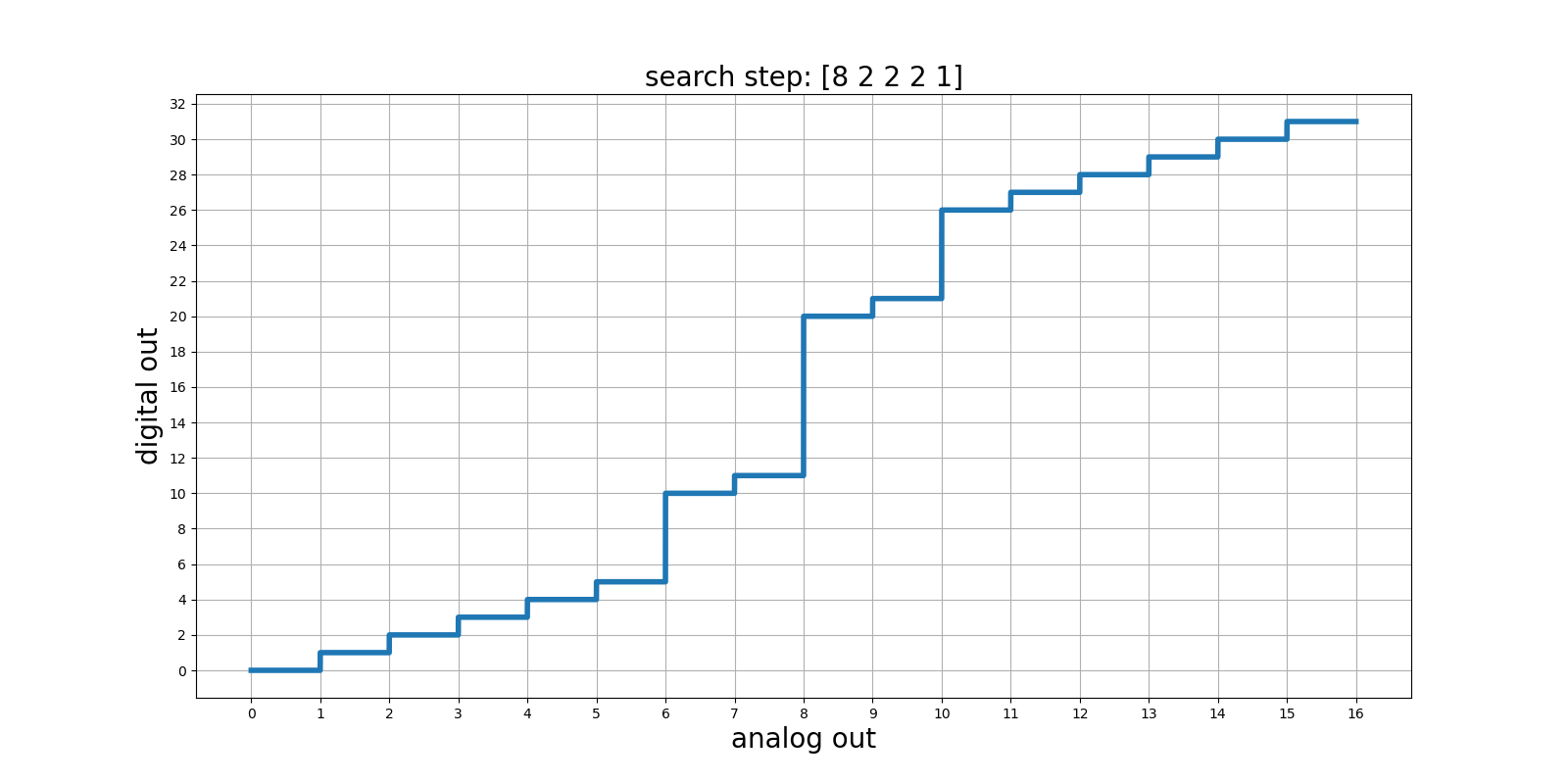
1 | import numpy as np |
ENOB vs. fixed radix
When the ADC is designed with a fixed radix, \(\alpha\) and the required number of conversion steps, \(M\)
the sum of all the step sizes \(s_{tot}\) \[ s_{tot} = \sum_{k=0}^{M-1} s_0 \alpha^k = s_0\frac{\alpha^M-1}{\alpha-1} \]
where \(s(i)\) is step size and \(i \in [0, 1, 2, M-1]\)
The effective number of bits, \(N\), can be calculated \[ N \leq \log 2\left(\frac{s_{tot} + s_0}{s_0}\right) = \frac{\alpha^M+\alpha-2}{\alpha-1} \]
Speed Benefit
TODO 📅
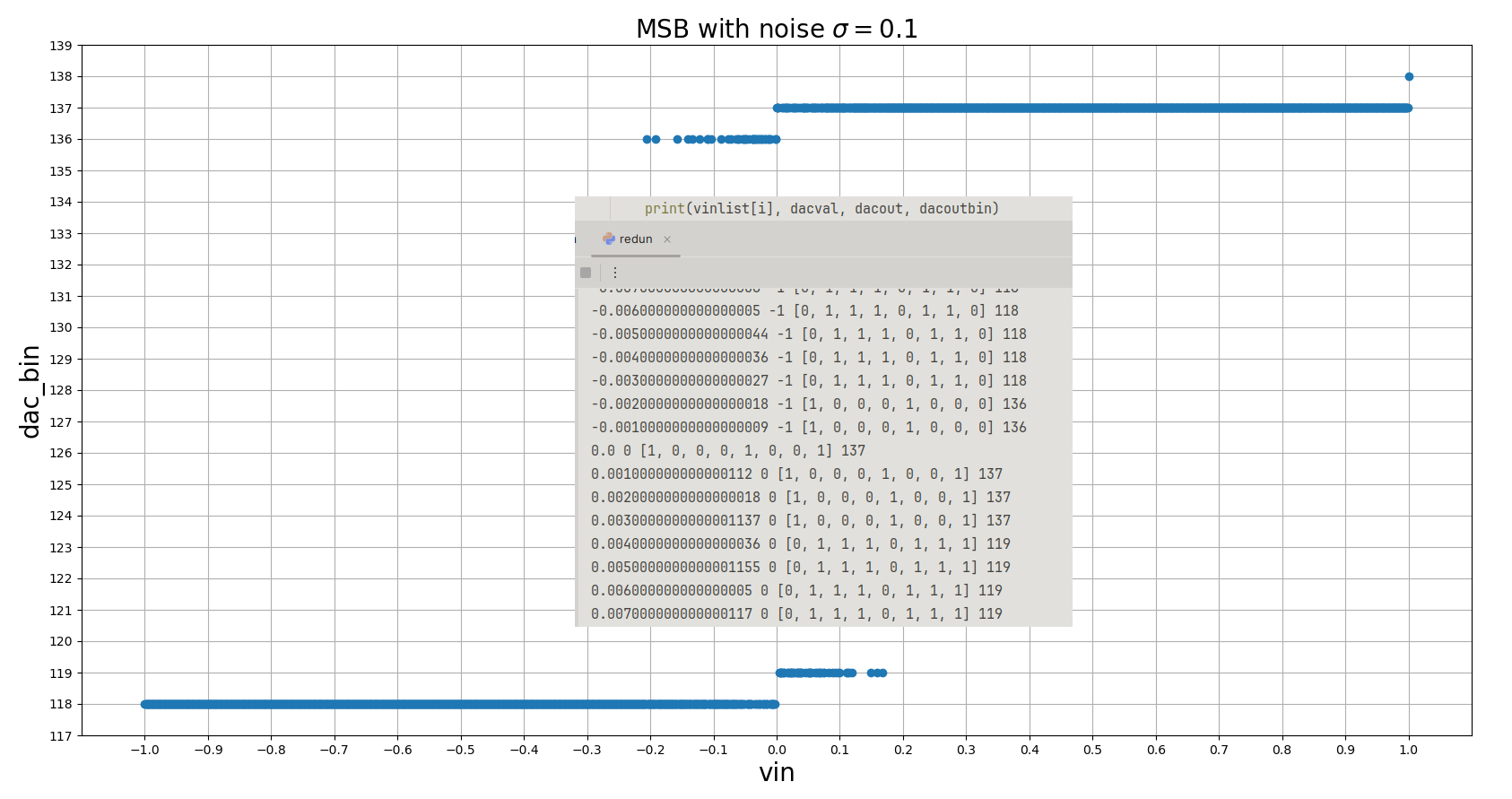
MSB with noise simualtion
CDAC
The charge redistribution capacitor network is used to sample the input signal and serves as a digital-to-analog converter (DAC) for creating and subtracting reference voltages
sampling charge \[ Q = V_{in} C_{tot} \] conversion charge \[ Q = -C_{tot}V_c + V_{ref}C_\Delta \] That is \[ V_c = \frac{C_\Delta}{C_{tot}}V_{ref} - V_{in} \]
CDAC is actually working as a capacitive divider during conversion phase, the charge of internal node retain (charge conservation law)
assuming \(\Delta V_i\) is applied to series capacitor \(C_1\) and \(C_2\)
\[
(\Delta V_i - \Delta V_x) C_1 = \Delta V_x \cdot C_2
\] Then \[
\Delta V_x = \frac{C_1}{C_1+C_2}\Delta V_i
\]
\(V_x= V_{x,0} + \Delta V_x\)
CDAC settling accuracy
\[\begin{align}
V_x(s) &= \frac{C_1+C_2}{RC_1C_2}\cdot
\frac{1}{s+\frac{C_1+C_2}{RC_1C_2}}\cdot V_i(s) \\
&= \frac{1}{\tau}\cdot \frac{1}{s+\frac{1}{\tau}}\cdot \frac{1}{s}\\
&= \frac{1}{\tau}\cdot \tau(\frac{1}{s} -
\frac{1}{s+\frac{1}{\tau}})=\frac{1}{s} - \frac{1}{s+\frac{1}{\tau}}
\end{align}\]
inverse Laplace Transform is \(V_x(t) = 1 - e^{-t/\tau}\)
\[\begin{align} V_y(s) &= V_x\frac{C_1}{C_1+C_2} \\ &= \frac{C_1}{C_1+C_2} \left(\frac{1}{s} - \frac{1}{s+\frac{1}{\tau}}\right)\\ \end{align}\]
inverse Laplace Transform is \(V_y(t) = \frac{C_1}{C_1+C_2}\left(1 - e^{-t/\tau}\right)\)
\(V_x(t)\) and \(V_y(t)\) prove that the settling time is same
\(\tau = R\frac{C_1C_2}{C_1+C_2}\), which means usually worst for MSB capacitor (largest)
both \(\tau\) and \(\Delta V\) are the maximum
A popular way to improve the settling behavior, again, is to employ unit-element DACs that statistically reduce the switching activities, which, unfortunately, exhibits unnecessary complications to the power, area and speed tradeoffs of the design
CDAC Energy Consumption
\[ E_{Vref} = \int P(t)dt = \int V_{ref} I(t) dt = V_{ref}\int I(t)dt = V_{ref}\cdot \Delta Q \]
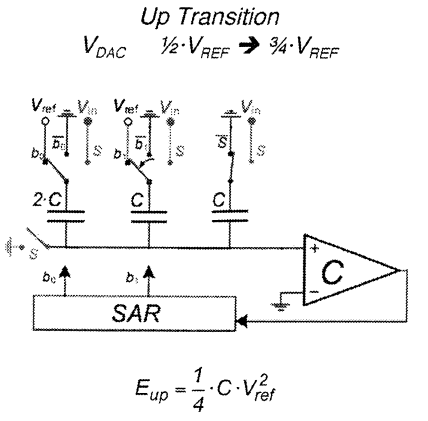
Given \(V_{c,0}=\frac{1}{2}V_{ref}-V_{in}\) and \(V_{c,1}=\frac{3}{4}V_{ref}-V_{in}\) \[\begin{align} Q_{b0,0} &= \left(V_{ref} - V_{c,0} \right)\cdot 2C = \left(\frac{1}{2}V_{ref}+V_{in} \right)\cdot 2C \\ Q_{b1,0} &= (0 - V_{c,0})\cdot C = \left(-\frac{1}{2}V_{ref}+V_{in} \right)\cdot C \\ Q_{b0,1} &= \left(V_{ref} - V_{c,1} \right)\cdot 2C = \left(\frac{1}{4}V_{ref}+V_{in} \right)\cdot 2C \\ Q_{b1,1} &= \left(V_{ref} - V_{c,1} \right)\cdot C = \left(\frac{1}{4}V_{ref}+V_{in} \right)\cdot C \end{align}\]
Therefore \[ E_{Vref} = V_{ref}\cdot (Q_{b0,1}+Q_{b1,1} - Q_{b0,0}-Q_{b1,0}) = \frac{1}{4}C V_{ref}^2 \]
CDAC total energy change \[\begin{align} \Delta E_{tot} &= \frac{1}{2}\cdot 2C \cdot (U_{2c,1}^2 - U_{2c,0}^2) + \frac{1}{2}\cdot C \cdot (U_{c,1}^2 - U_{c,0}^2) + \frac{1}{2}\cdot C \cdot (U_{c1,1}^2 - U_{c1,0}^2) \\ &= \left(-\frac{3}{16}V_{ref}^2 - \frac{1}{2}V_{ref}V_{in} - \frac{3}{32}V_{ref}^2+\frac{3}{4}V_{ref}V_{vin} + \frac{5}{32}V_{ref}^2-\frac{1}{4}V_{ref}V_{in}\right)C \\ &= -\frac{1}{8}CV_{ref}^2 \end{align}\]
alternative method
\[
\Delta E_{tot} = \frac{1}{2}\cdot\frac{3}{4}C\cdot
V_{ref}^2 - \frac{1}{2}\cdot C\cdot V_{ref}^2 = -\frac{1}{8}CV_{ref}^2
\]
The total energy decreases by \(-\frac{1}{8}CV_{ref}^2\), though \(V_{ref}\) provides \(\frac{1}{4}C V_{ref}^2\)
The charge redistribution change the CDAC energy
\[ E_{c,0} = \frac{1}{2}CV^2 \] After charge redistribution \[ E_{c,1} = \frac{1}{2}\cdot 2C\cdot \left(\frac{1}{2}V\right)^2 = \frac{1}{4}CV^2 \]
That make sense, charge redistribution consume energy
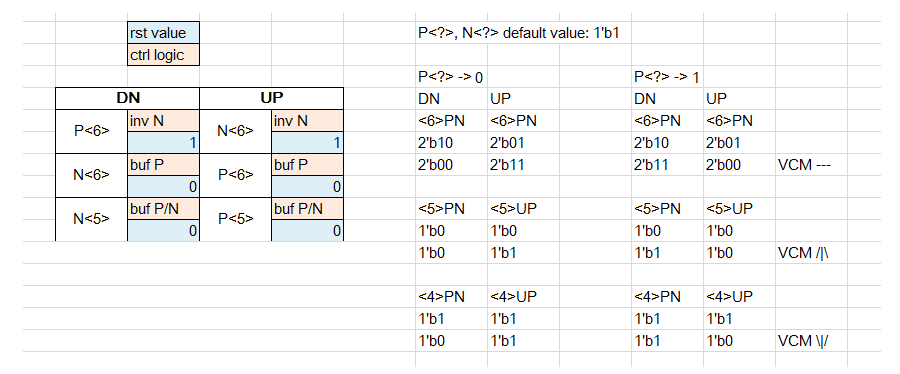
CDAC structure
CDAC with constant common-mode voltage
Comparator
Comparator input cap effect
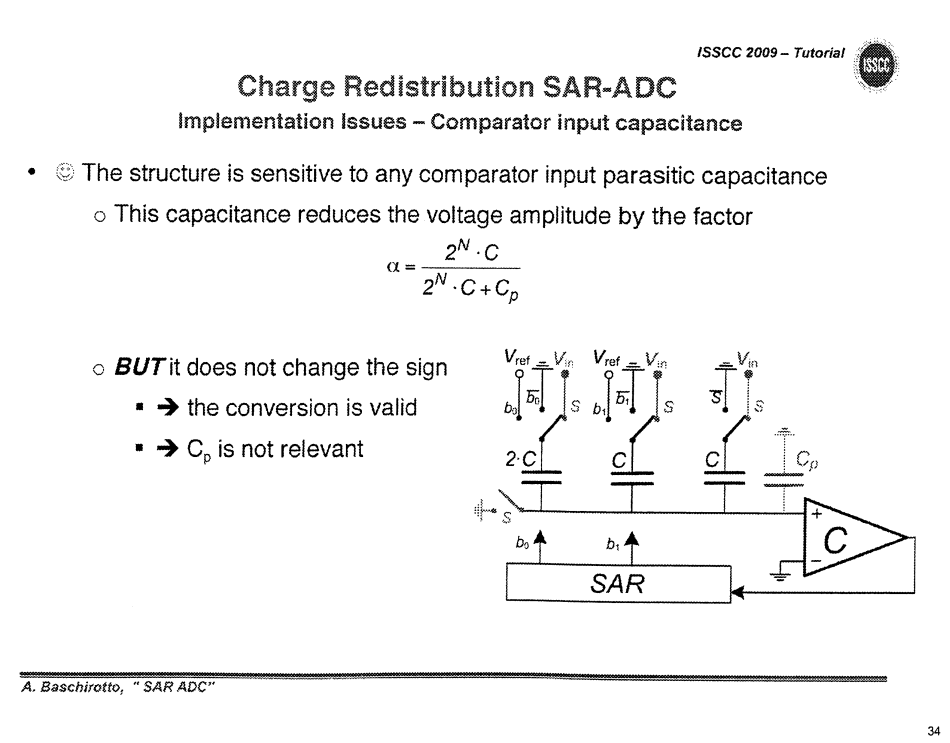 \[
-V_{in}\cdot 2^N C = V_c (2^N C + C_p)
\] Then \(V_c = -\frac{2^N C}{2^N C +
C_p}V_{in}\), i.e. this capacitance reduce the voltage amplitude
by the factor
\[
-V_{in}\cdot 2^N C = V_c (2^N C + C_p)
\] Then \(V_c = -\frac{2^N C}{2^N C +
C_p}V_{in}\), i.e. this capacitance reduce the voltage amplitude
by the factor
During conversion \[\begin{align} V_c &= -\frac{2^N C}{2^N C + C_p}V_{in} +V_{ref}\sum_{n=0}^{N-1} \frac{b_n\cdot2^n C}{2^N C + C_p} \\ &= \frac{2^N C}{2^N C + C_p}\left(-V_{in} + V_{ref}\sum_{n=0}^{N-1}\frac{b_n }{2^{N-n}} \right) \end{align}\]
That is, it does not change the sign
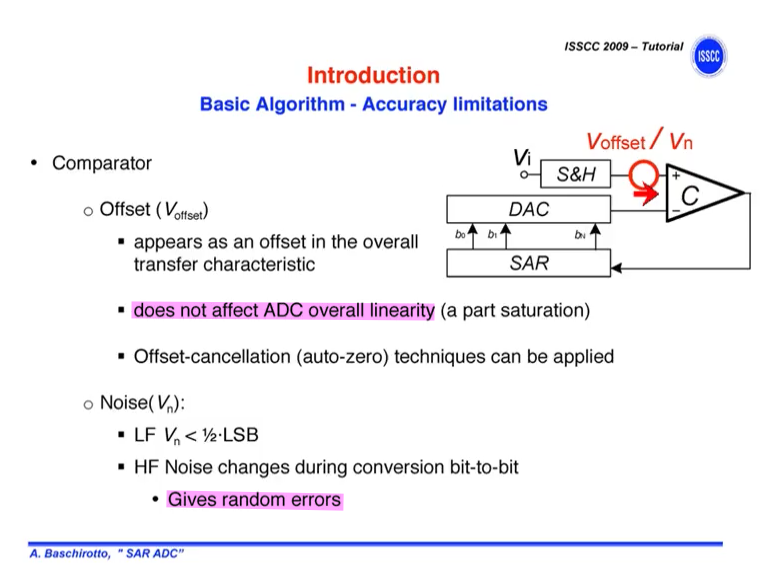
Comparator offset effect
Synchronous SAR ADC
It also divides a full conversion into several comparison stages in a way similar to the pipeline ADC, except the algorithm is executed sequentially rather than in parallel as in the pipeline case.
However, the sequential operation of the SA algorithm has traditionally been a limitation in achieving high-speed operation
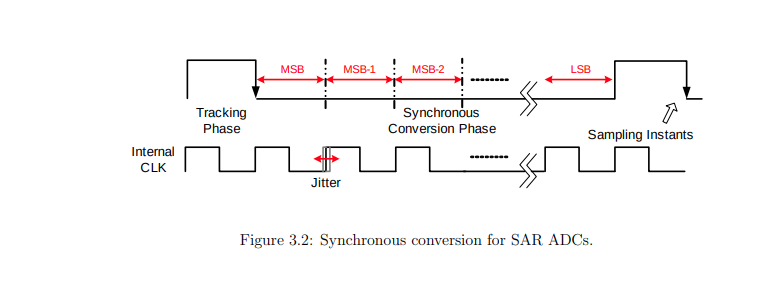
- a clock running at least \((N + 1) \cdot F_s\) is required for an \(N\)-bit converter with conversion rate of \(F_s\)
- every clock cycle has to tolerate the worst case comparison time
- every clock cycle requires margin for the clock jitter
The power and speed limitations of a synchronous SA design comes largely from the high-speed internal clock
Split Arrary CDAC
Split capacitor, double-array cap
attenuation capacitance \(C_a\)
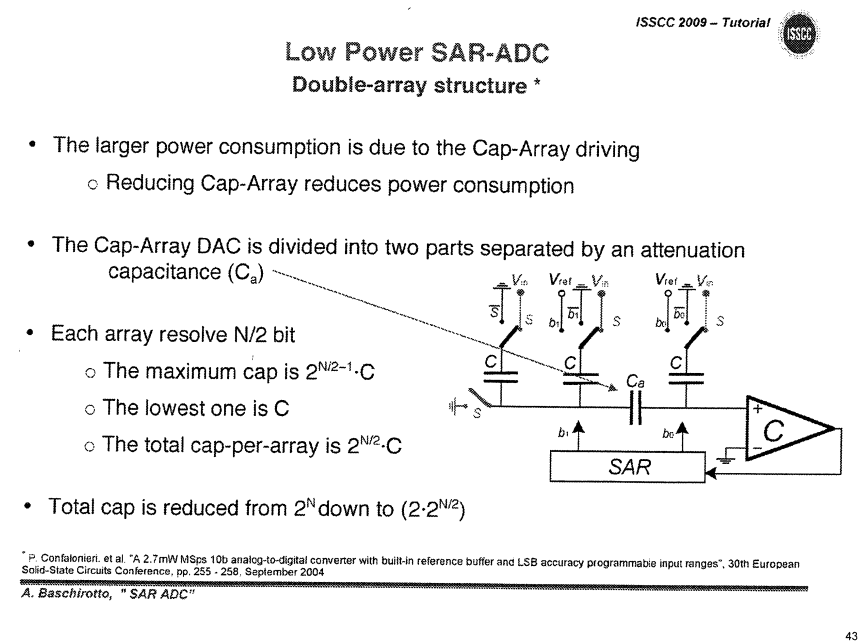
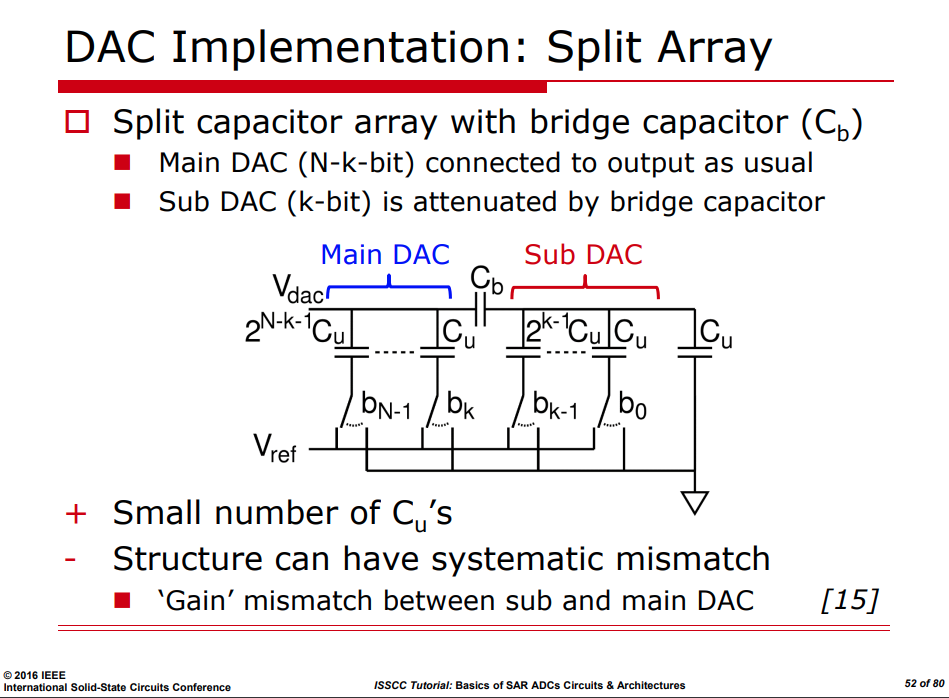
\[\begin{align} \Delta V_{dac} &= \frac{1}{2}b_3+\frac{1}{4}b_2+\frac{1}{4}\left(\frac{1}{2}b_1+\frac{1}{4}b_0 \right) \\ &= \frac{1}{2}b_3+\frac{1}{4}b_2 + \frac{1}{8}b_1+\frac{1}{16}b_0 \end{align}\]
Asynchronous SAR ADC
The comparator itself trigger the next bit-conversion cycle as soon as the present bit decision has been taken
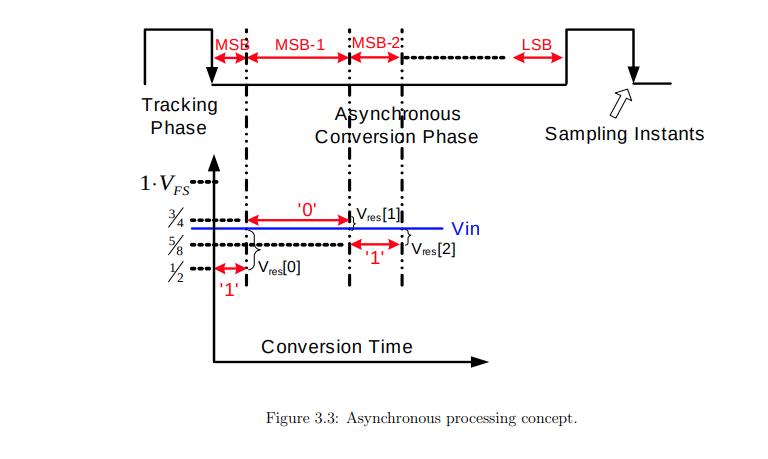

The maximum resolving time reduction between synchronous and asynchronous case is two fold
comparator metastable state
when the input is sufficiently small. The time needed for the comparator outputs to fully resolve may take arbitrarily long
In this case, the ready signal generator should still set the flag and the decision result is simply taken from the previous value stored in the SR latch
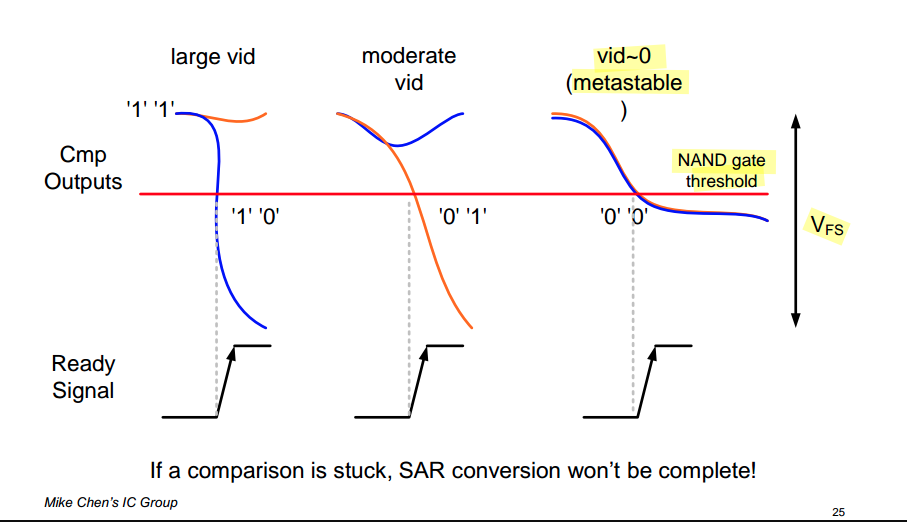
both outputs (\(Q_p\) and \(Q_n\)) will drop together, NAND is inverter actually
The transition point of this NAND gate is skewed to eliminate metastability issues arising when the input differential voltage level is small (comparator)
reference
Andrea Baschirotto, "T6: SAR ADCs" ISSCC2009
Pieter Harpe, ISSCC 2016 Tutorial: "Basics of SAR ADCs Circuits & Architectures"
Mike Shuo-Wei Chen and R. W. Brodersen, "A 6-bit 600-MS/s 5.3-mW Asynchronous ADC in 0.13-μm CMOS," in IEEE Journal of Solid-State Circuits, vol. 41, no. 12, pp. 2669-2680, Dec. 2006 [pdf, slides]
—. "Power Efficient System and A/D Converter Design for Ultra-Wideband Radio" [http://www2.eecs.berkeley.edu/Pubs/TechRpts/2006/EECS-2006-71.pdf]
—. "Asynchronous SAR ADC: Past, Present and Beyond" [https://viterbi-web.usc.edu/~swchen/index_files/async_sar_tutorial_chen_final.pdf]
C. -C. Liu, S. -J. Chang, G. -Y. Huang and Y. -Z. Lin, "A 10-bit 50-MS/s SAR ADC With a Monotonic Capacitor Switching Procedure," in IEEE Journal of Solid-State Circuits, vol. 45, no. 4, pp. 731-740, April 2010 [https://sci-hub.se/10.1109/JSSC.2010.2042254]
L. Jie et al., "An Overview of Noise-Shaping SAR ADC: From Fundamentals to the Frontier," in IEEE Open Journal of the Solid-State Circuits Society, vol. 1, pp. 149-161, 2021 [pdf]
W. Liu, P. Huang and Y. Chiu, "A 12-bit, 45-MS/s, 3-mW Redundant Successive-Approximation-Register Analog-to-Digital Converter With Digital Calibration," in IEEE Journal of Solid-State Circuits, vol. 46, no. 11, pp. 2661-2672, Nov. 2011 [https://sci-hub.st/10.1109/JSSC.2011.2163556]