Analog Techniques

Posted on Edited on In

Push-Pull

TODO 📅

Rinaldo Castello, "LINEARIZATION TECHNIQUES FOR PUSH-PULL AMPLIFIERS" [https://www.ieeetoronto.ca/wp-content/uploads/2020/06/AMPLIFIERS_Stanf_Tor_2016_Last.pdf]

Rail-to-Rail Op amp

[https://mixsignal.wordpress.com/wp-content/uploads/2013/03/689-604rail2rail.pdf]

[https://toshiba.semicon-storage.com/ap-en/semiconductor/knowledge/faq/linear_opamp/what-does-rail-to-rail-mean.html]

TODO 📅

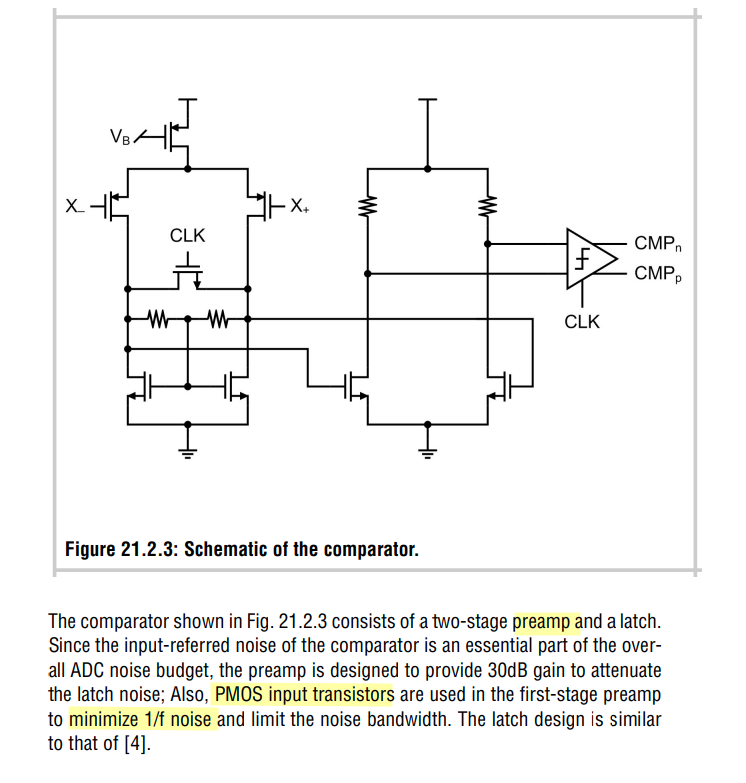
self-biased active loading

image-20251029213156015

Vishal Saxena "CMOS Comparator Design Extra Slides" [https://www.eecis.udel.edu/~vsaxena/courses/ece614/Handouts/Comparator%20Slides.pdf]

preampSong202412181018

W. Liu, P. Huang and Y. Chiu, "A 12b 22.5/45MS/s 3.0mW 0.059mm2 CMOS SAR ADC achieving over 90dB SFDR," 2010 IEEE International Solid-State Circuits Conference - (ISSCC), San Francisco, CA, USA, 2010 [https://sci-hub.se/10.1109/ISSCC.2010.5433830]

image-20250805230555464

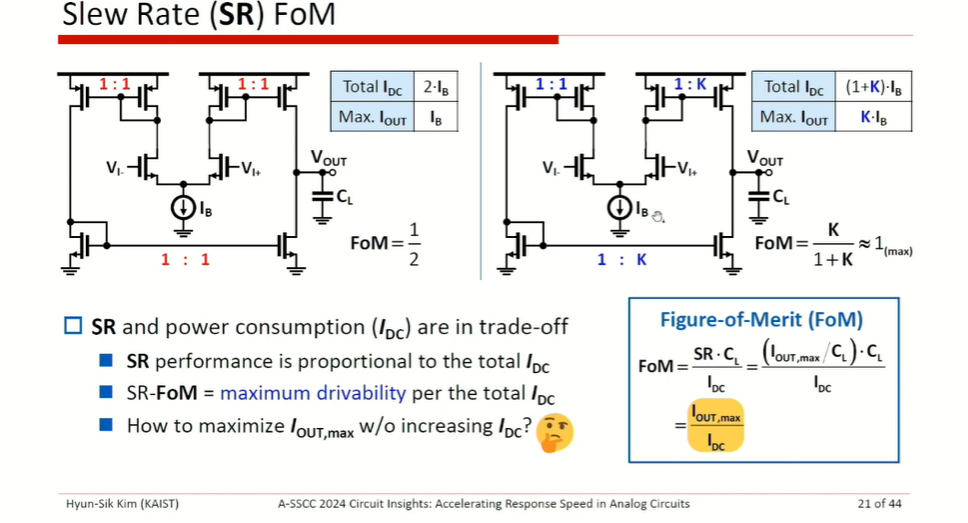
Slewing in Folded-Cascode Op Amps

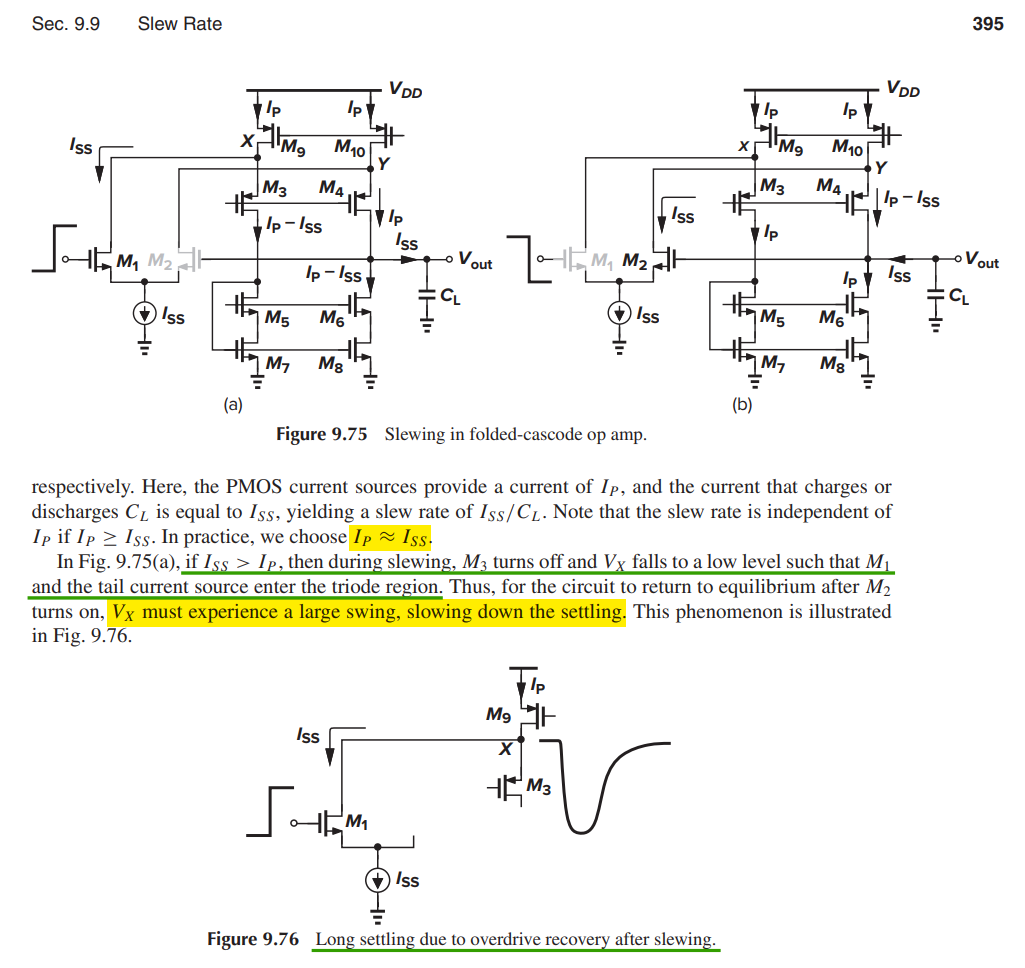
image-20240817161915989

In practice, we choose \(I_P \simeq I_{SS}\)

image-20240817162418938

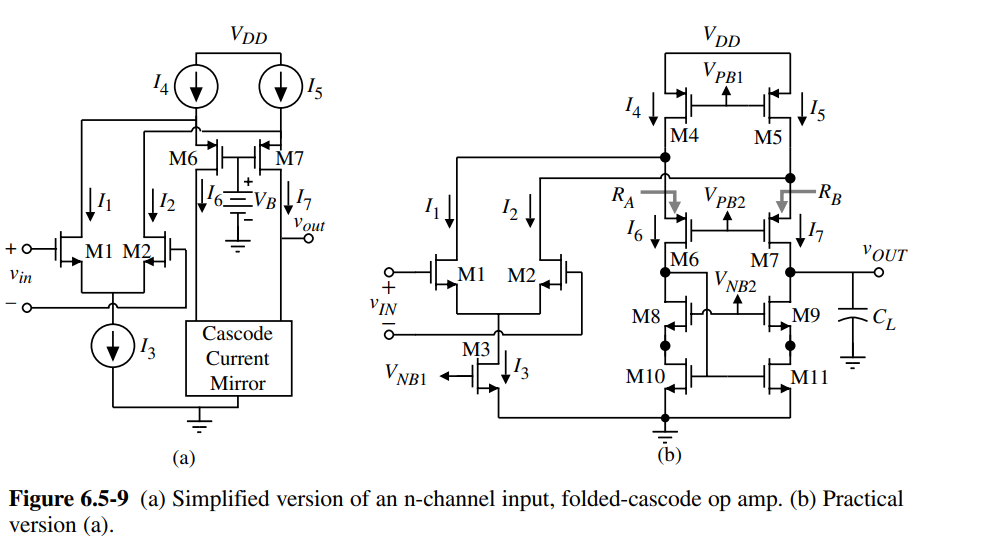
image-20240817162127452

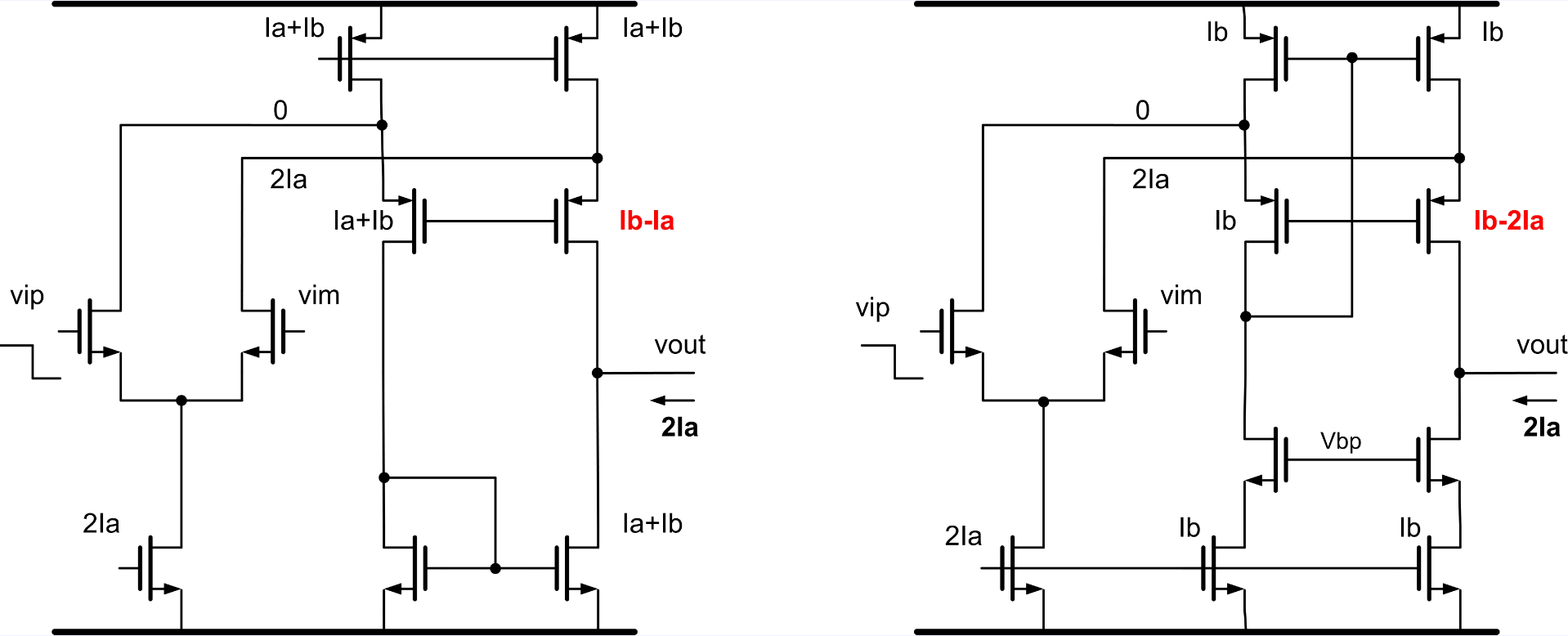
image-20240816175038971

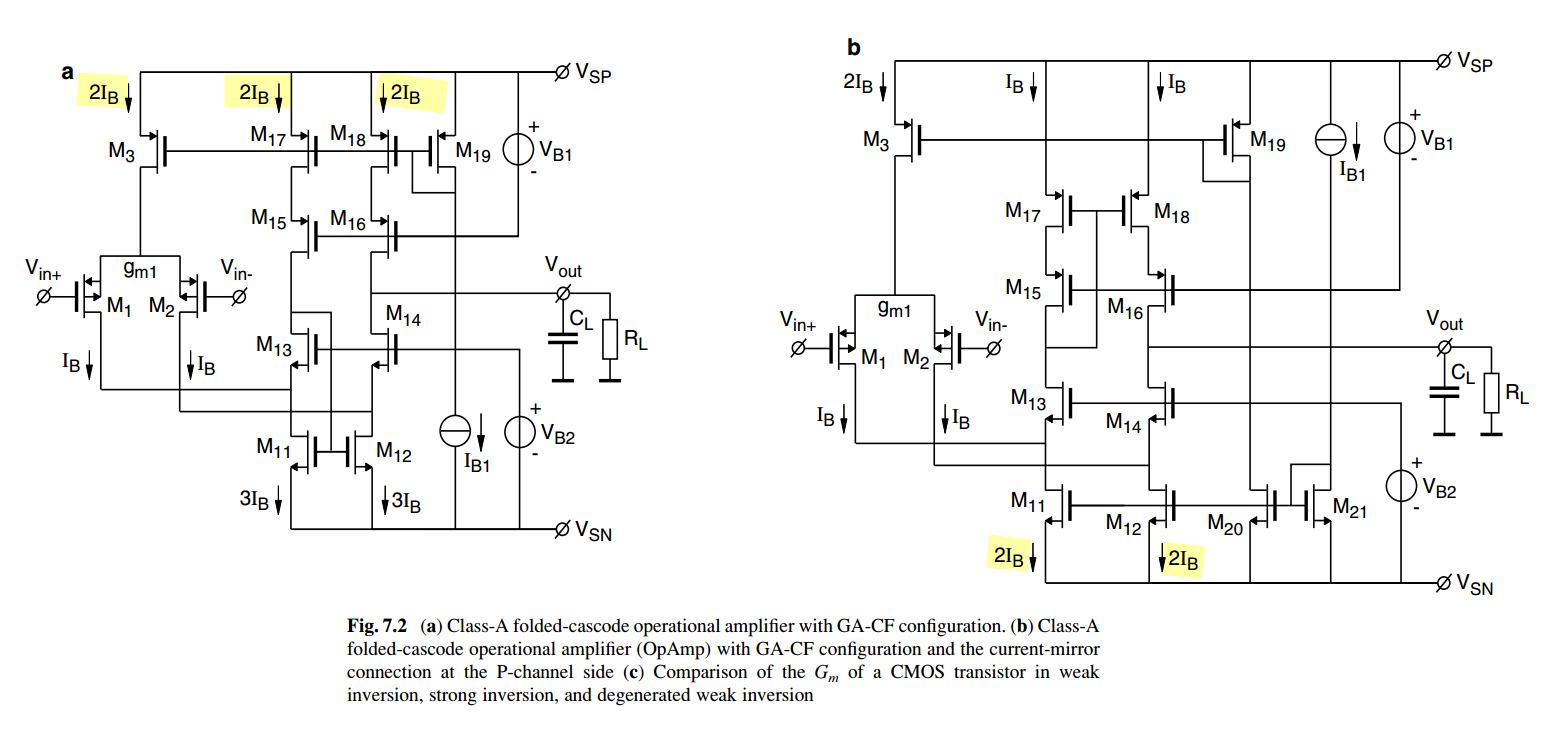
Avoid zero current in cascodes

  • left circuit

    \(I_b \gt I_a\)

  • right circuit

    \(I_b \gt 2I_a\)

Huijsing, J. H. (2017). Operational Amplifiers: Theory and Design. (3 ed.) Springer

[https://bbs.eetop.cn/forum.php?mod=redirect&goto=findpost&ptid=995502&pid=11548528]

image-20250922233947643

Response Speed in Analog Circuits

Hyun-Sik Kim, KAIST, A-SSCC 2024 Circuit Insights: FT3 Accelerating Response Speed in Analog Circuits [link]

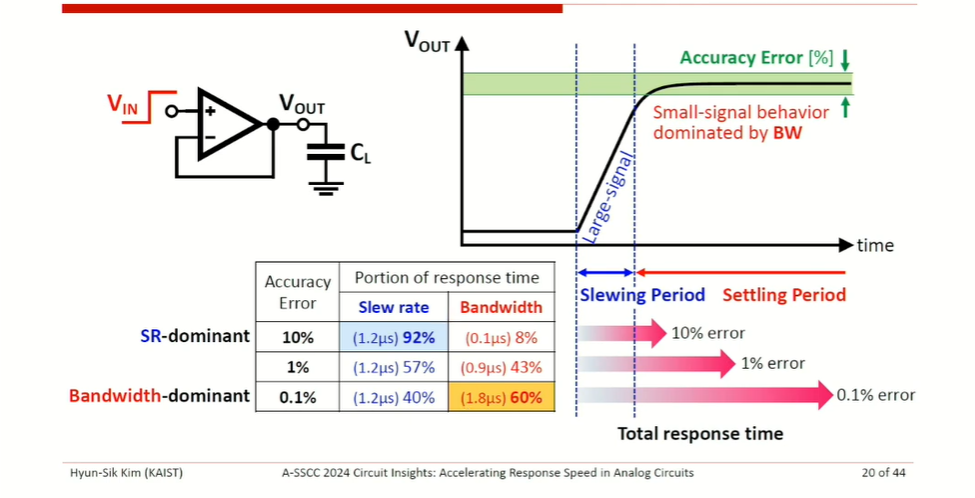
image-20250105085449759

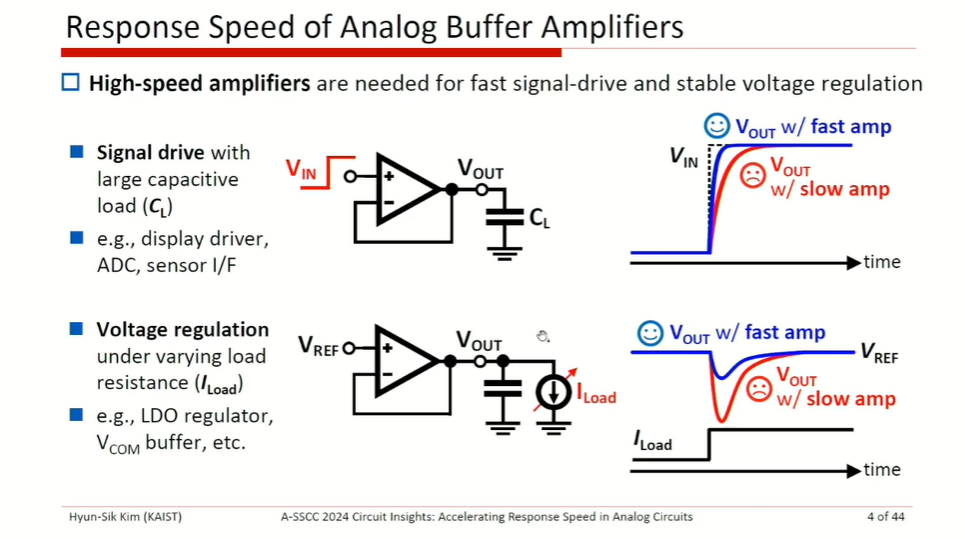
image-20250105072433452

Bandwidth limitation

image-20250105072748483

image-20250105073322162

image-20250105090203938image-20250105090204188

slew rate limitation

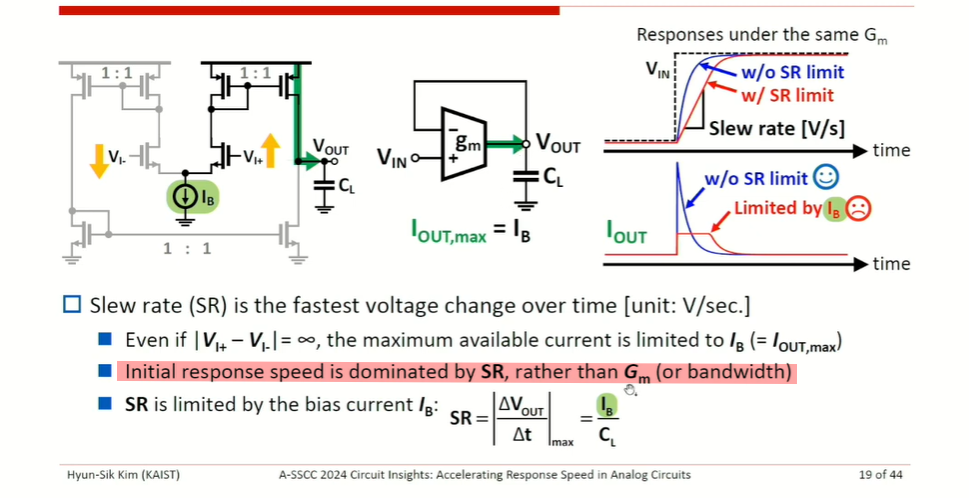
image-20250105083039901

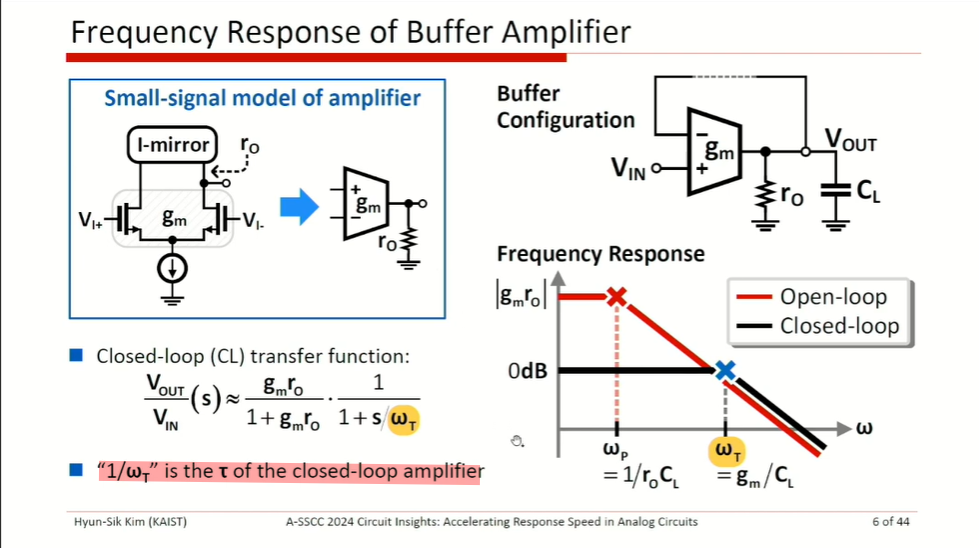
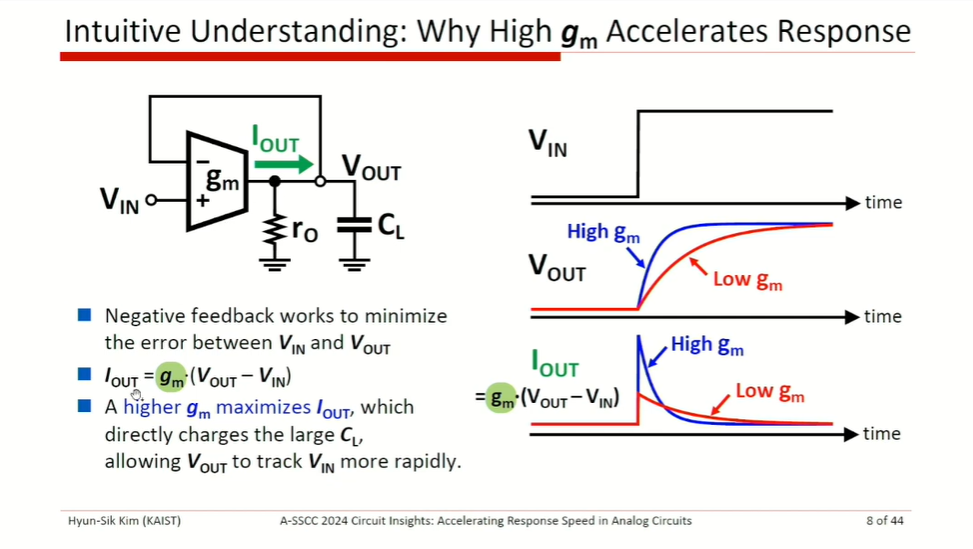
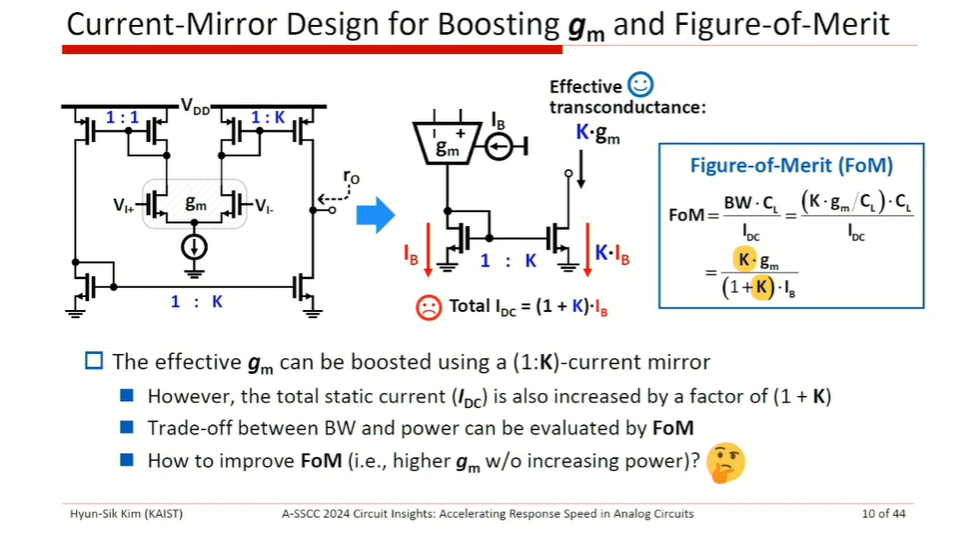
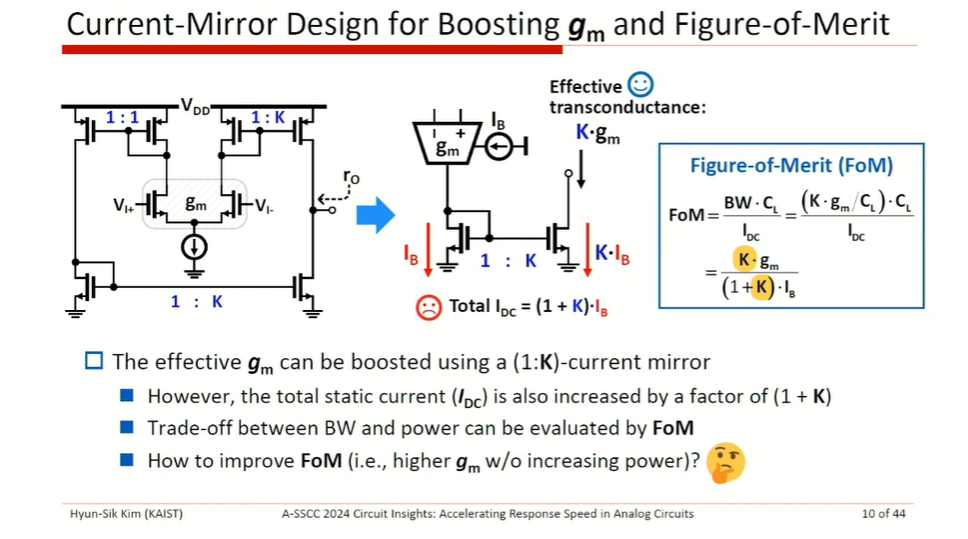
Assuming linear response \[ V_o(t) = 1 - e^{-\omega_T t} \]

\[ \frac{dV_o}{dt} = \omega_Te^{-\omega_T t} = \frac{g_m}{C_L}e^{-\omega_T t} = \frac{g_m}{I_B}\cdot \frac{I_B}{C_L}\cdot e^{-\omega_T t} \gt \frac{I_B}{C_L} \]

where \(\frac{g_m}{I_B} e^{-\omega_T t} \gt 1\) at initial response

Therefore, initial response speed is dominated by SR, rather than \(G_m\) (or bandwidth)

image-20250105090105095

MOS parasitic Rd&Rs, Cd&Cs

Decrease the parasitic R&C

priority: \(R_s \gt R_d\), \(C_s \gt C_d\)

source follower

A. Sheikholeslami, "Voltage Follower, Part III [Circuit Intuitions]," in IEEE Solid-State Circuits Magazine, vol. 15, no. 2, pp. 14-26, Spring 2023, doi: 10.1109/MSSC.2023.3269457

—, ESSCIRC2023 Circuit Insights [https://youtu.be/2xFIZM5_FPw?si=536cMdIXyIny27Uk]

—, CICC2025 Circuit Insights: From Simple to Super Source Follower [https://youtu.be/CWfMKltPIQ8?si=s0npv2GSQKYBv513]

Paul R. Gray. 2009. Analysis and Design of Analog Integrated Circuits (5th. ed.). Wiley Publishing. [pdf]

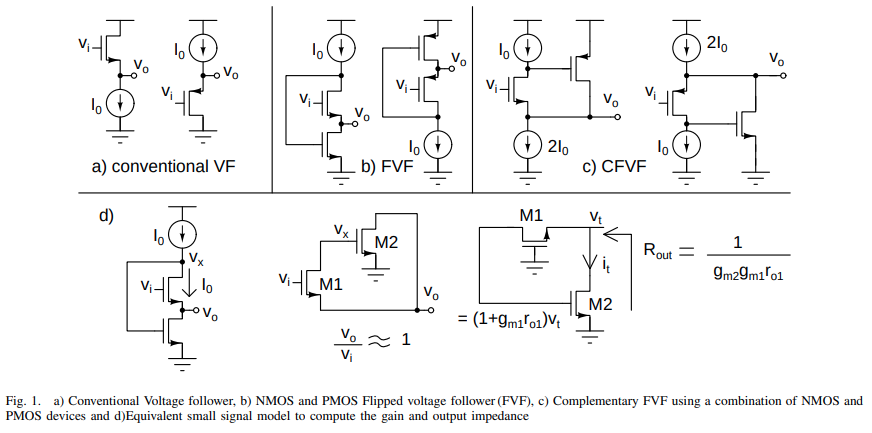
Super-source follower (SSF)

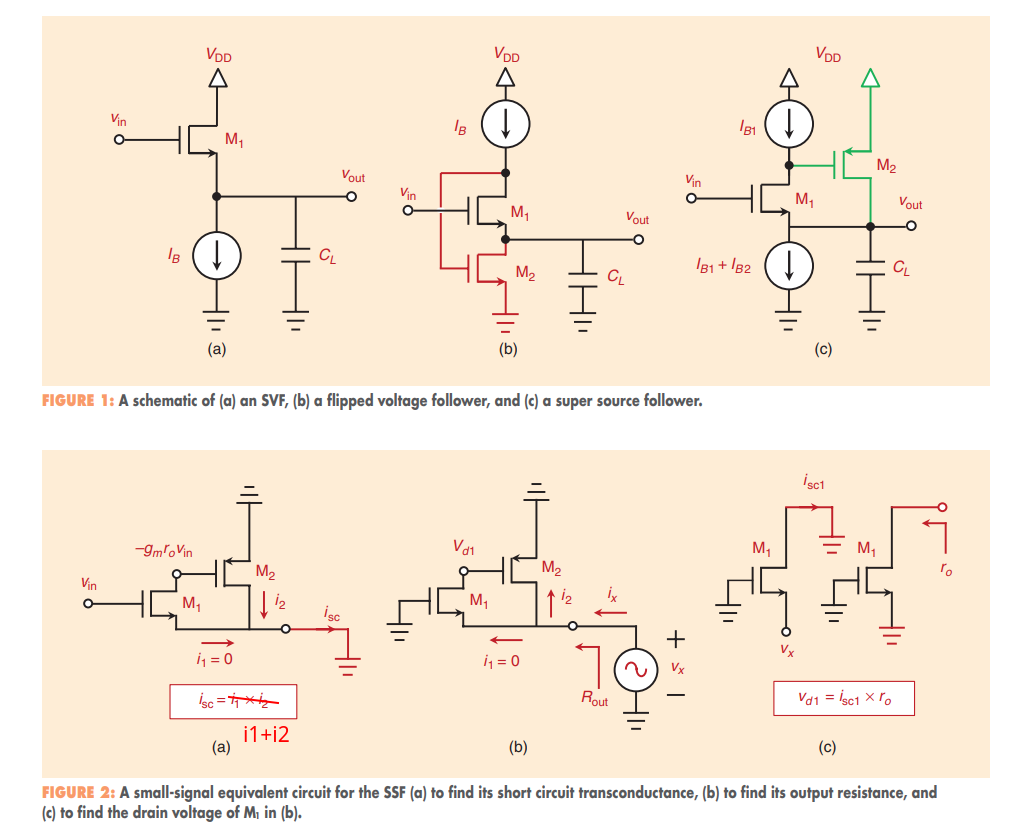
image-20240924213742877

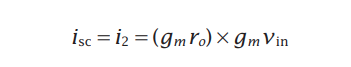
image-20240924213845608

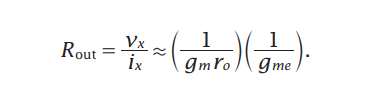
image-20240924213853954

Flipped Voltage Follower (FVF)

image-20240921110019881

image-20240921113630249

T&H buffer in ADC

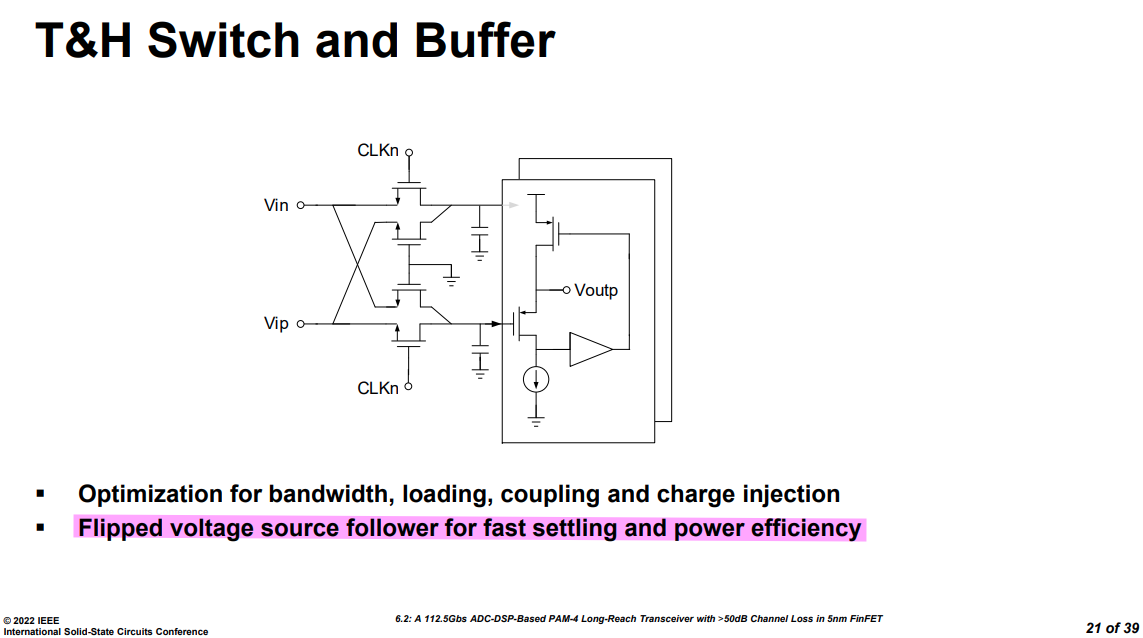
image-20240923200147070

[https://www.linkedin.com/posts/chembiyan-t-0b34b910_flipped-voltage-follower-fvf-basics-activity-7118482840803020800-qwyX?utm_source=share&utm_medium=member_desktop]

Z. Guo et al., "A 112.5Gb/s ADC-DSP-Based PAM-4 Long-Reach Transceiver with >50dB Channel Loss in 5nm FinFET," 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 2022, pp. 116-118, doi: 10.1109/ISSCC42614.2022.9731650.

Double Differential pair

\(V_\text{ip}\) and \(V_\text{im}\) are input, \(V_\text{rp}\) and \(V_\text{rm}\) are reference voltage \[ V_o = A_v(\overline{V_\text{ip} - V_\text{im}} - \overline{V_\text{rp} - V_\text{rm}}) \]

2diffpair.drawio

In differential comparison mode, the feedback loop ensure \(V_\text{ip} = V_\text{rp}\), \(V_\text{im} = V_\text{rm}\) in the end

assume input and reference common voltage are same

Pros of (b)

  • larger input range i.e., \(\gt \pm \sqrt{2}V_\text{ov}\) of (a), it works even one differential is off due to lower voltage
  • larger \(g_m\) (smaller input difference of pair)

Cons of (b)

  • sensitive to the difference of common voltage between \(V_\text{ip}\), \(V_\text{im}\) and \(V_\text{rp}\), \(V_\text{rm}\)

common-mode voltage difference

doublepair_cm.drawio

copy aforementioned formula here for convenience \[ V_o = A_v(\overline{V_\text{ip} - V_\text{im}} - \overline{V_\text{rp} - V_\text{rm}}) \]

at sample phase \(V_\text{ip}= V_\text{im}= V_\text{cmi}\) and \(V_\text{rp}= V_\text{rm}= V_\text{cmr}\)

  • \(I_\text{ip0}= I_\text{im0} = I_\text{i0}\)
  • \(I_\text{rp0}= I_\text{rm0} = I_\text{r0}\)

i.e. \(\overline{I_\text{ip} + I_\text{rm}} - \overline{I_\text{im} + I_\text{rp}} = 0\)

at compare start

  • \(V_\text{ip}= V_\text{im}= V_\text{cmi}\) and \(V_\text{rp}= V_\text{cmr}+\Delta\), \(V_\text{rp}= V_\text{cmr}-\Delta\)

  • \(I_\text{ip}\lt I_\text{ip0}\), \(I_\text{rp} \gt I_\text{rp0}\)

  • \(I_\text{im}\gt I_\text{im0}\), \(I_\text{rm} \lt I_\text{rm0}\)

i.e. \(\overline{I_\text{ip} + I_\text{rm}} - \overline{I_\text{im} + I_\text{rp}} \lt 0\), we need to increase \(V_\text{ip}\) and decrease \(V_\text{im}\).

at the compare finish

\[\begin{align} V_\text{ip}= V_\text{cmi} + \Delta \\ V_\text{im}= V_\text{cmi} - \Delta \end{align}\]

and \(I_\text{ip0}= I_\text{im0} = I_\text{i0}\), \(I_\text{rp0}= I_\text{rm0} = I_\text{r0}\)

i.e. \(\overline{I_\text{ip} + I_\text{rm}} - \overline{I_\text{im} + I_\text{rp}} = 0\)

If \(V_\text{cmr} - V_\text{cmi} = \sqrt{2}V_{OV} + \delta\), and \(\delta \gt 0\). one transistor carries the entire tail current

  • \(I_\text{ip} =0\) and \(I_\text{rp} = I_{SS}\), all the time

At the end, \(V_\text{im} = V_\text{cmi} - (\Delta - \delta)\), the error is \(\delta\)

In closing, \(V_\text{cmr} - V_\text{cmi} \lt \sqrt{2}V_{OV}\) for normal work

Furthermore, the difference between \(V_\text{cmr}\) and \(V_\text{cmi}\) should be minimized due to limited impedance of current source and input pair offset

In the end \[ V_\text{cmr} - V_\text{cmi} \lt \sqrt{2}V_{OV} - V_{OS} \]

Under the condition, every transistor of pairs are on in equilibrium

pair mismatch

diff_mismatch_connect.drawio

\[\begin{align} I_{SE} &= g_m(\sigma_{vth,0} + \sigma_{vth,1}) \\ I_{DE} &= g_m(\sigma_{vth,0} + \sigma_{vth,1}) \end{align}\]

The input equivalient offset voltage \[\begin{align} V_{os,SE} &= \frac{I_{SE}}{2g_m} = \frac{\sigma_{vth,0} + \sigma_{vth,1}}{2} \\ V_{os,DE} &= \frac{I_{DE}}{g_m} = \sigma_{vth,0} + \sigma_{vth,1} \end{align}\]

Then \[\begin{align} \sigma_{vos,SE} &= \sqrt{\frac{2\sigma_{vth}^2}{4}} = \frac{\sigma_{vth}}{\sqrt{2}} \\ \sigma_{vos,DE} &= \sqrt{2\sigma_{vth}^2} = \sqrt{2}\sigma_{vth} \end{align}\]

We obtain \[ \sigma_{vos,DE} = 2\sigma_{vos,SE} \]

Input Differential pair

Todd Brooks, Broadcom "Input Programmable Gain Amplifier (PGA) Design for ADC Signal Conditioning" [https://classes.engr.oregonstate.edu/eecs/spring2021/ece627/Lecture%20Notes/OSU%20Classroom%20Presentaton%20042511.ppt]

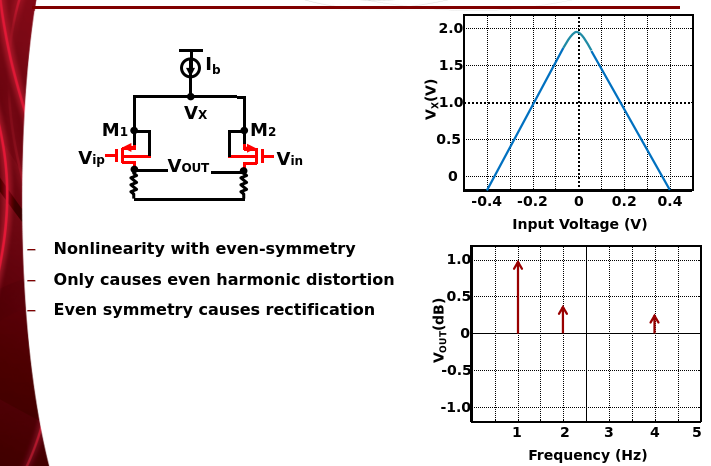
DM Distortion

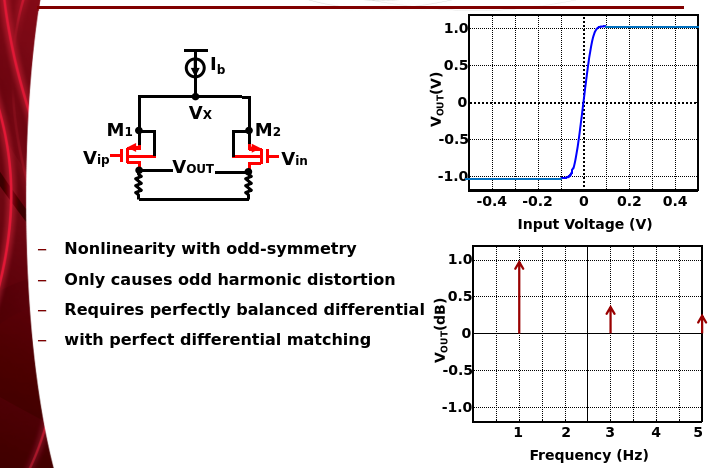
image-20241027095213326

CM Distortion

image-20241027095248946

Resistive Degeneration

Resistive degeneration in differential pairs serves as one major technique for linear amplifier

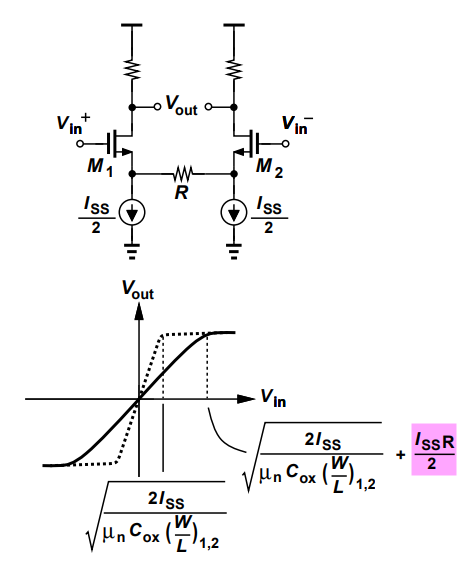
image-20240824132739726

The linear region for CMOS differential pair would be extended by \(±I_{SS}R/2\) as all of \(I_{SS}/2\) flows through \(R\). \[\begin{align} V_{in}^+ -V_{in}^- &= V_{OV} + V_{TH}+\frac{I_{SS}}{2}R - V_{TH} \\ &= \sqrt{\frac{2I_{SS}}{\mu_nC_{OX}\frac{W}{L}}} + \frac{I_{SS}R}{2} \end{align}\]

Jri Lee, "Communication Integrated Circuits." https://cc.ee.ntu.edu.tw/~jrilee/publications/Comm_IC.pdf

Figure 14.12, Design of Analog CMOS Integrated Circuits, Second Edition [https://electrovolt.ir/wp-content/uploads/2014/08/Design-of-Analog-CMOS-Integrated-Circuit-2nd-Edition-ElectroVolt.ir_.pdf]

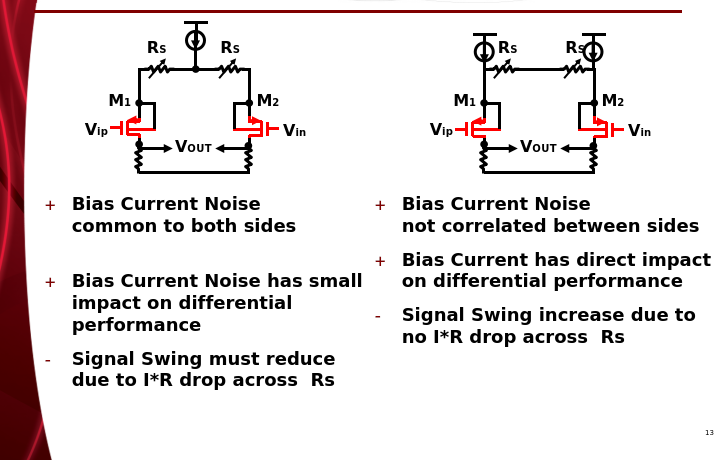
Biasing Tradeoffs in Resistive-Degenerated Diff Pair

image-20241027095520556