Time-Interleaved ADCs

Posted on Edited on In

Frequency Domain Model

f-mdl.drawio

image-20250903212048962

Skew (Timing Mismatch) Calibration

TODO 📅

M. Gu, Y. Tao, Y. Zhong, L. Jie and N. Sun, "Timing-Skew Calibration Techniques in Time-Interleaved ADCs," in IEEE Open Journal of the Solid-State Circuits Society, vol. 5, pp. 1-10, 2025 [https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=10804623]

S. Chen, L. Wang, H. Zhang, R. Murugesu, D. Dunwell, A. Chan Carusone, “All-Digital Calibration of Timing Mismatch Error in Time-Interleaved Analog-to-Digital Converters,” IEEE Transactions on VLSI Systems, Sept. 2017. [PDF, slides]

B. Razavi, "Problem of timing mismatch in interleaved ADCs," Proceedings of the IEEE 2012 Custom Integrated Circuits Conference, San Jose, CA, USA, 2012 [https://www.seas.ucla.edu/brweb/papers/Conferences/BRCICC12.pdf]

resync (alignment)

TODO 📅

Multi-Phase Clock Generation (MPCG)

TODO 📅

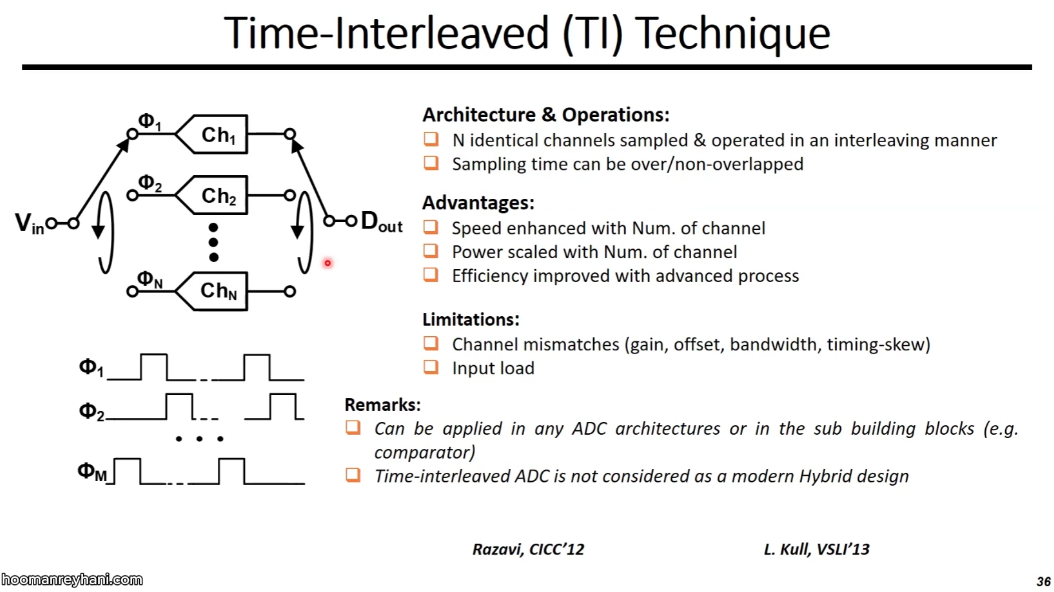
image-20250611222614434

Interleaver

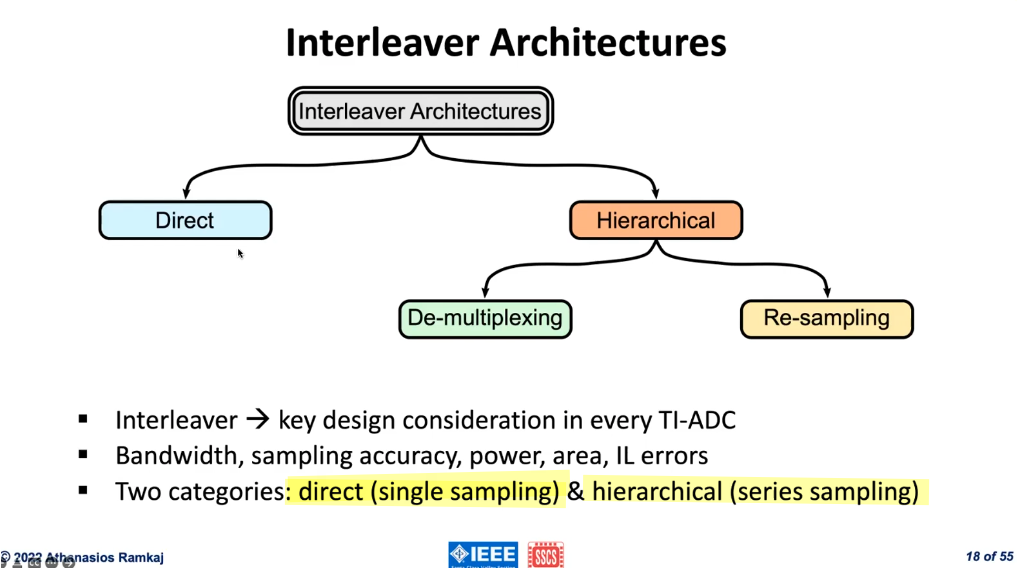
image-20250621094704819

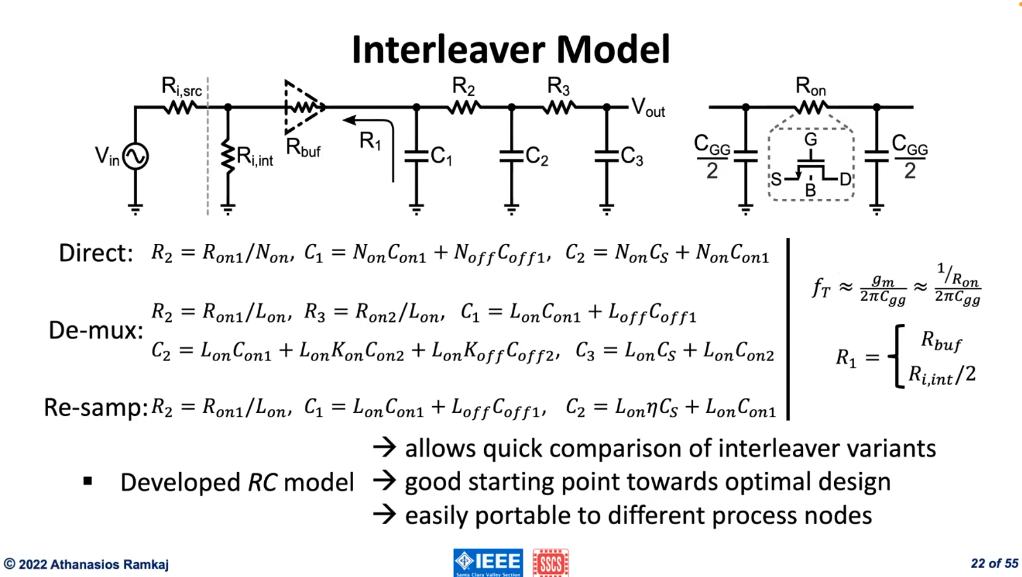
Direct Interleaver

image-20250621101542418

similar to increase the resolution of the flash ADC with more parallel comparators

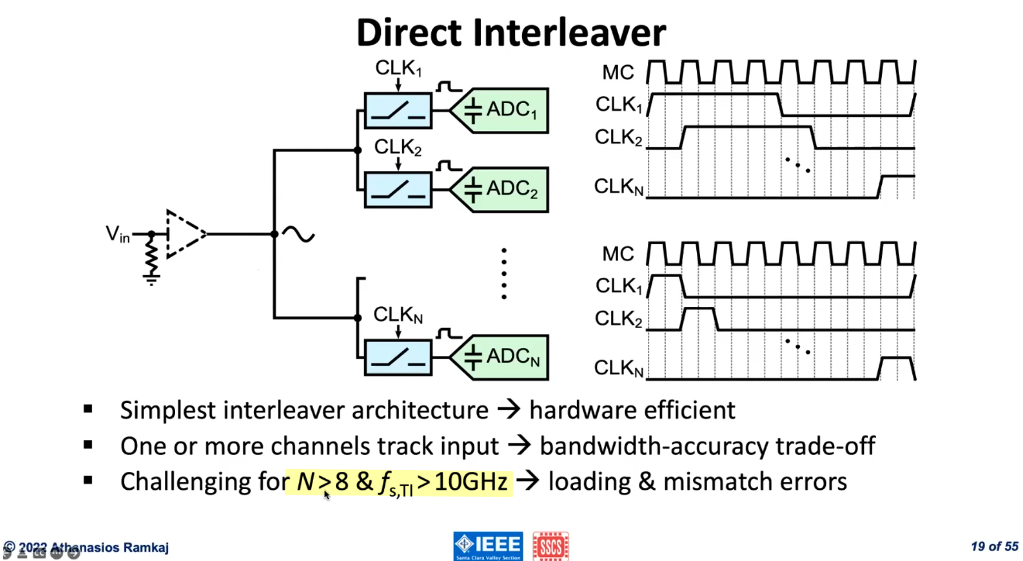
De-multiplexing Interleaver

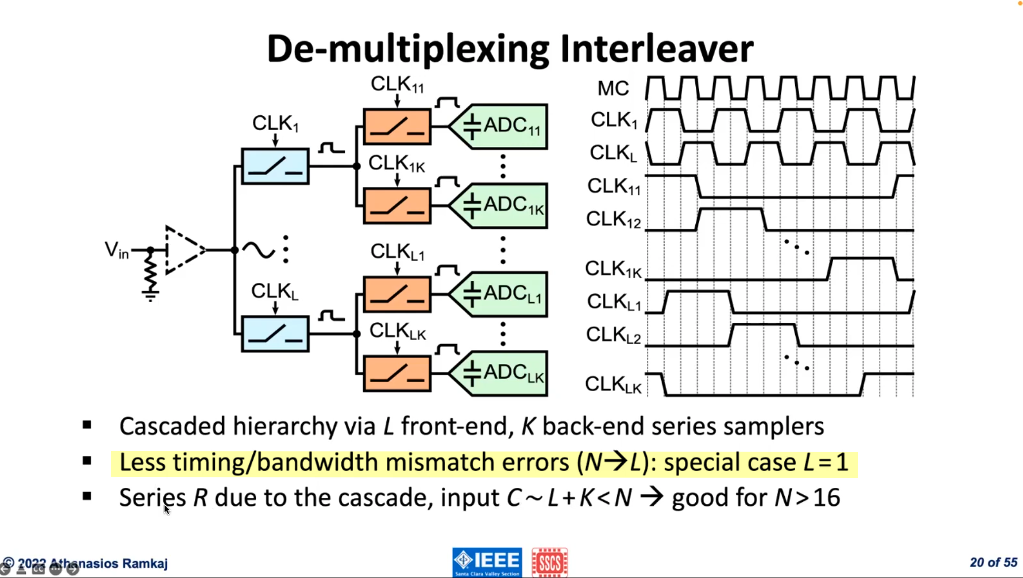
image-20250621103205333

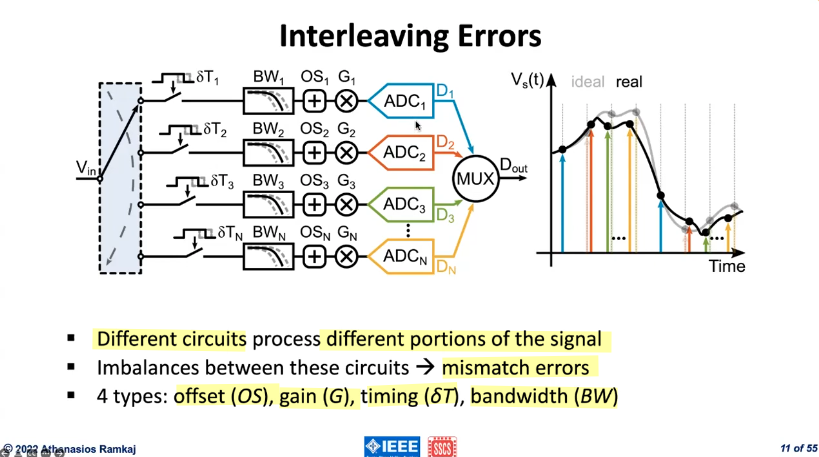
it is the front-end samplers that determine timing/bandwidth mismatch errors

Re-sampling Interleaver

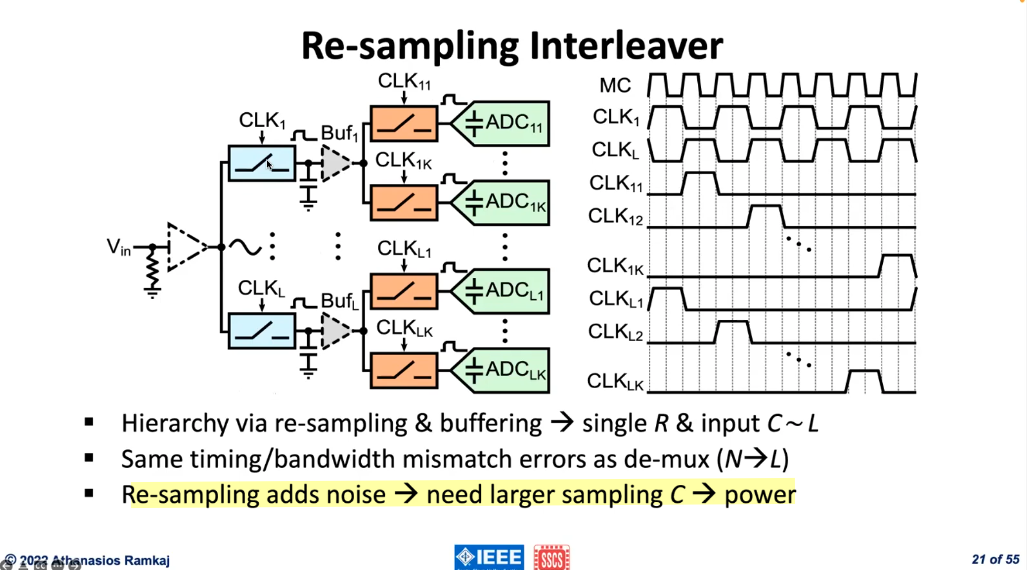
image-20250621111119041

back-end re-sampling occur after the front-end, two \(\frac{KT}{C}\) contribution in total noise (De-multiplexing Interleaver only one \(\frac{KT}{C}\))

without buffer, charging distribution reduce signal and reduce SNR, but buffers give excess noise

Interleaver Model

image-20250621112657111

Interleaving Errors

image-20250621072540691

image-20250621093552545

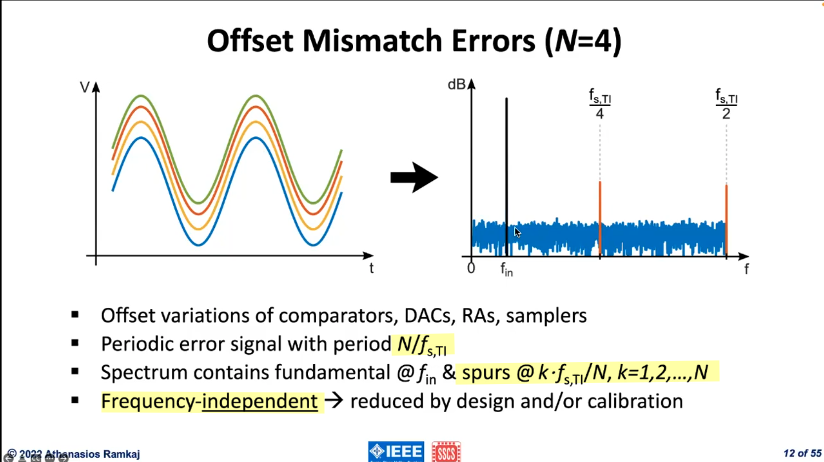
Offset Mismatch Error

image-20250621072621033

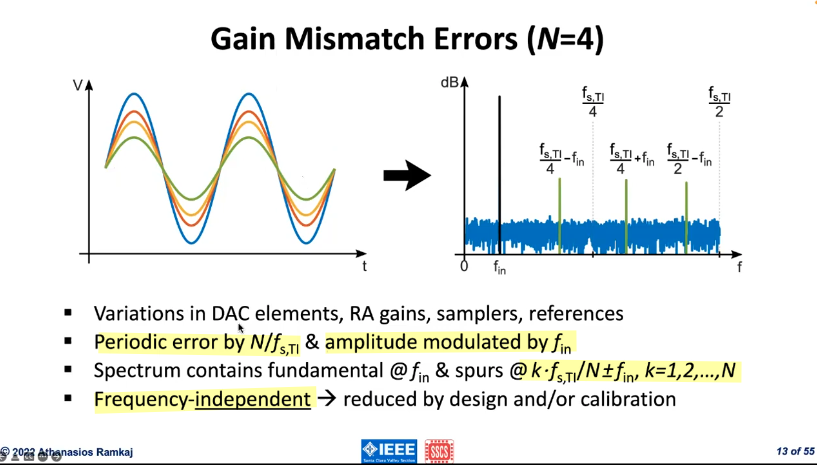
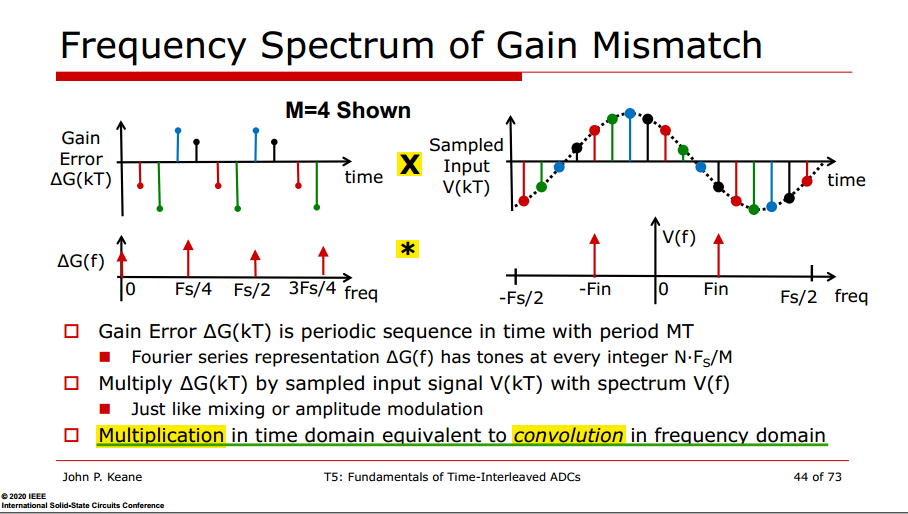
Gain Mismatch Error

image-20250621072824275

image-20250621072944516

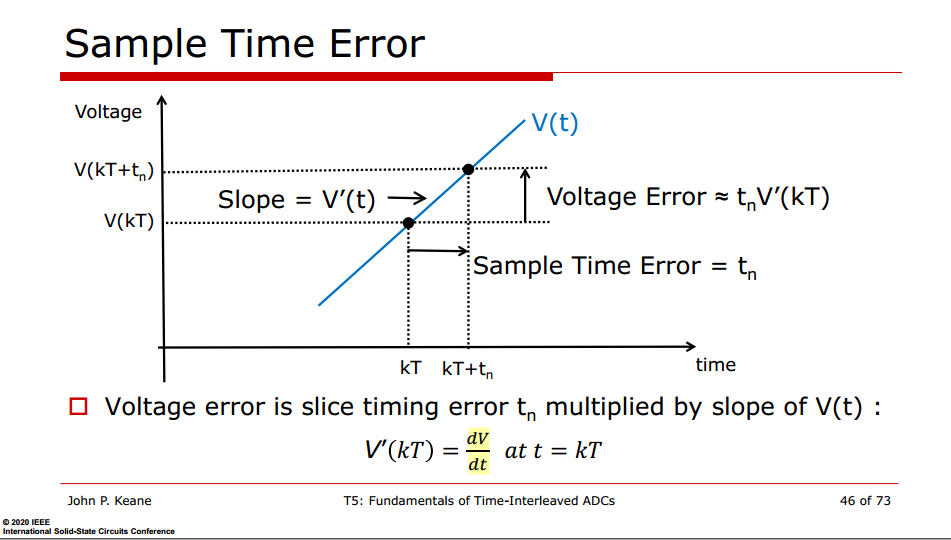
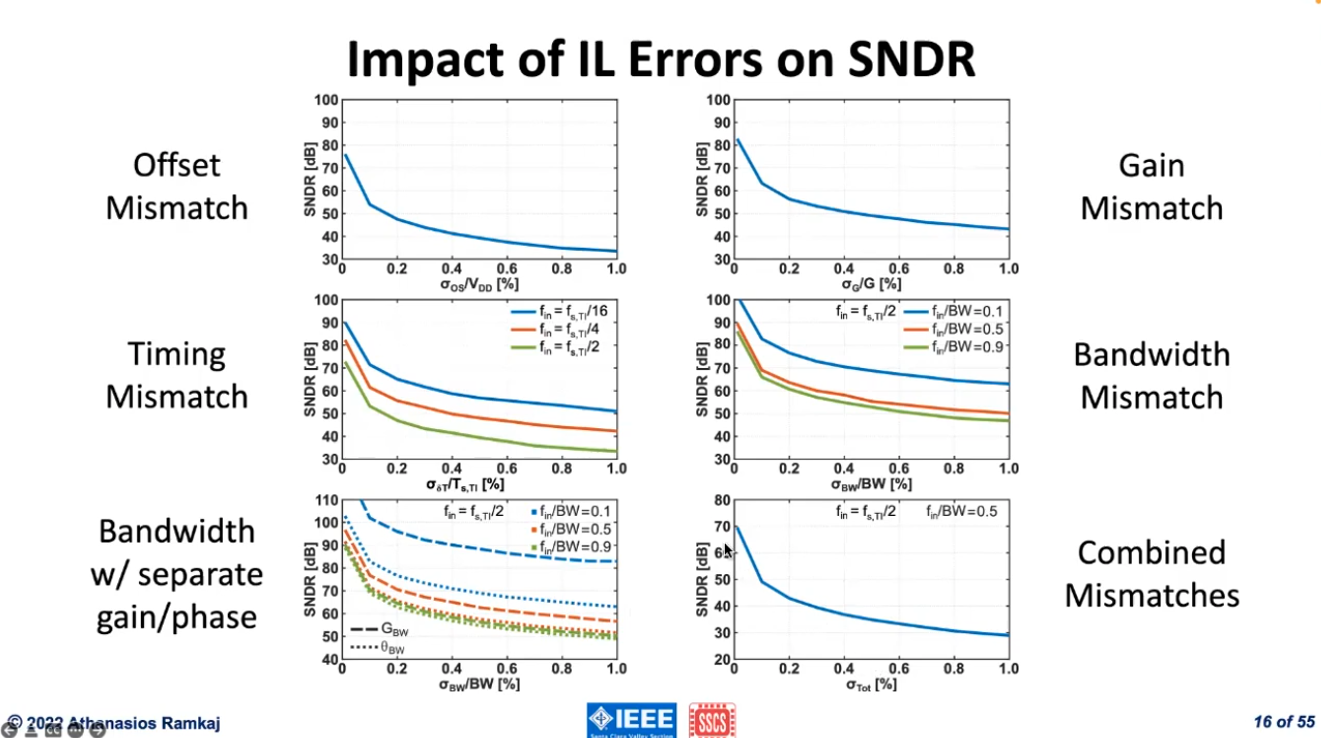
Timing Mismatch Error

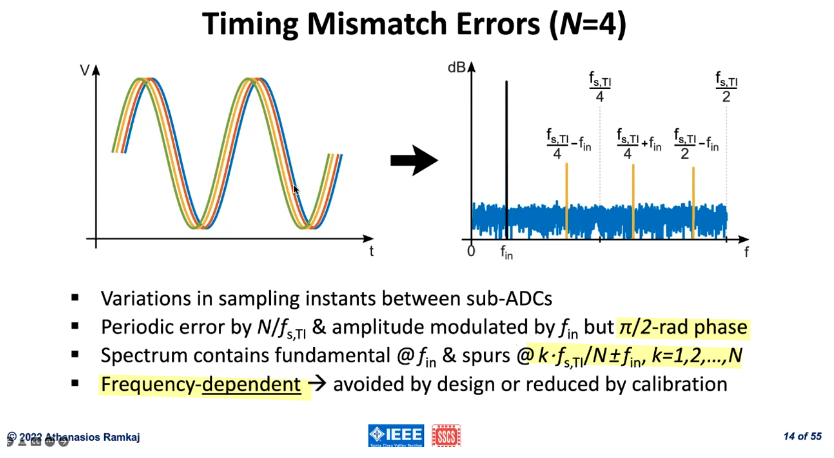
image-20250621090407014

\(\pi/2\)-rad phase: the maximum error occurs at the zero crossing and not on the peaks (Gain Mismatch error)

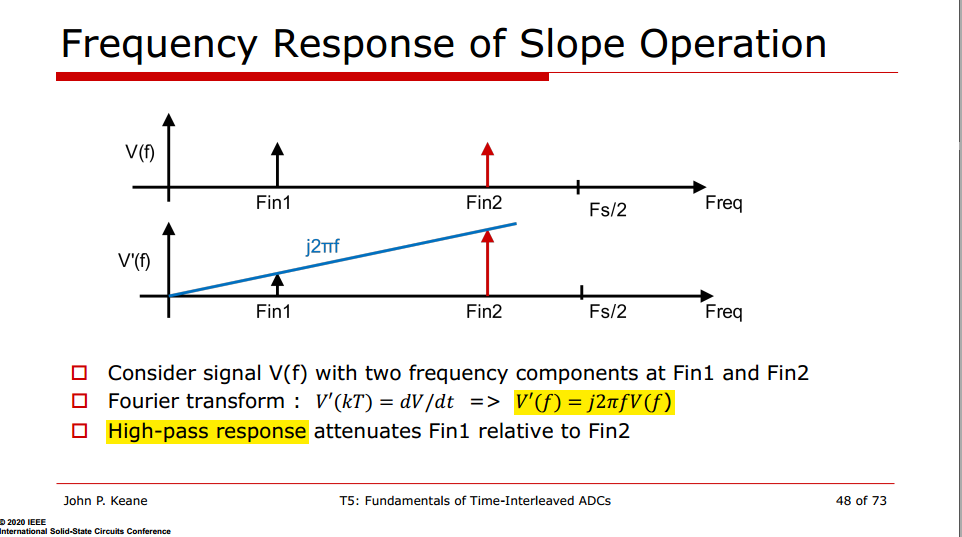
Frequency-dependent: the higher frequency input signal \(f_\text{in}\), the larger error becomes

image-20250621091024424

image-20250621091047339

\(\pi/2\) phase shift \[ e^{j\pi/2} = j \] frequency-dependent \[ V^{'} \propto f \]

In time domain \[ \frac{d\sin(\omega t)}{dt} = \omega \cos(\omega t) \propto \omega \]

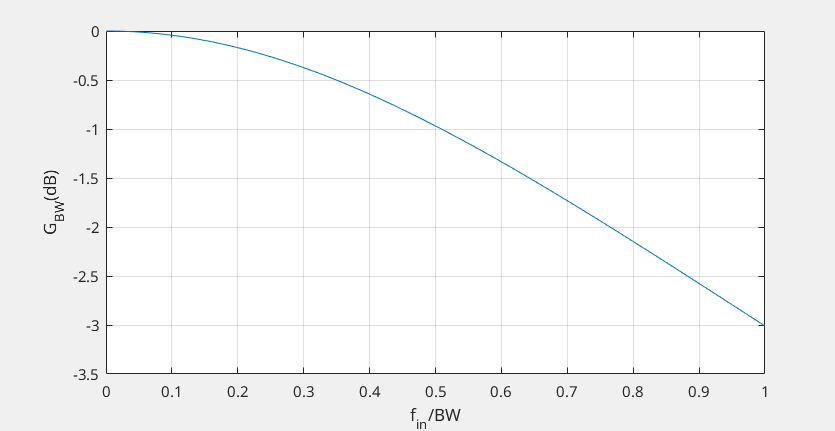
Bandwidth Mismatch Errors

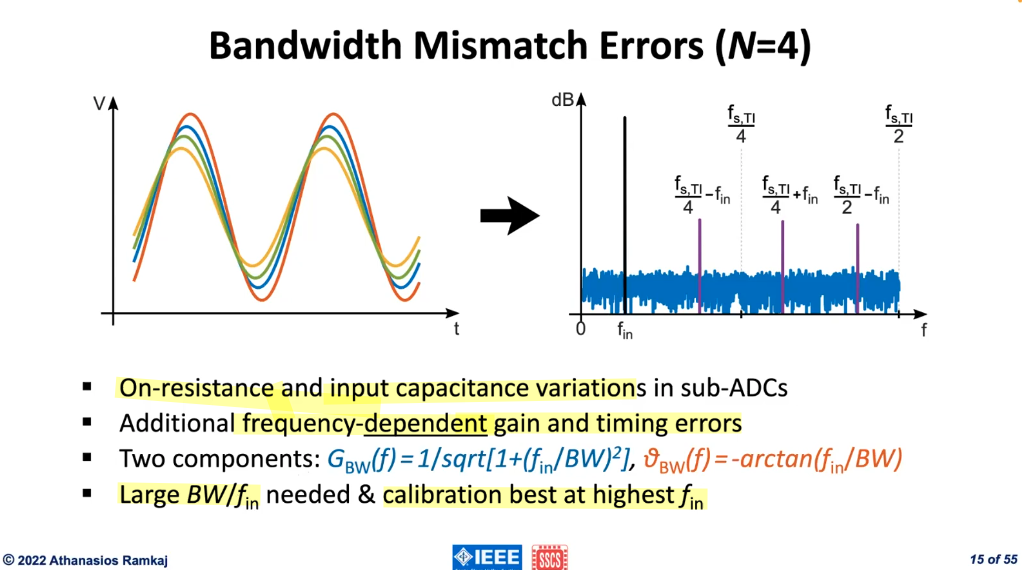
image-20250621092214162

image-20250621093321623

Overlapping versus Non-overlapping track time

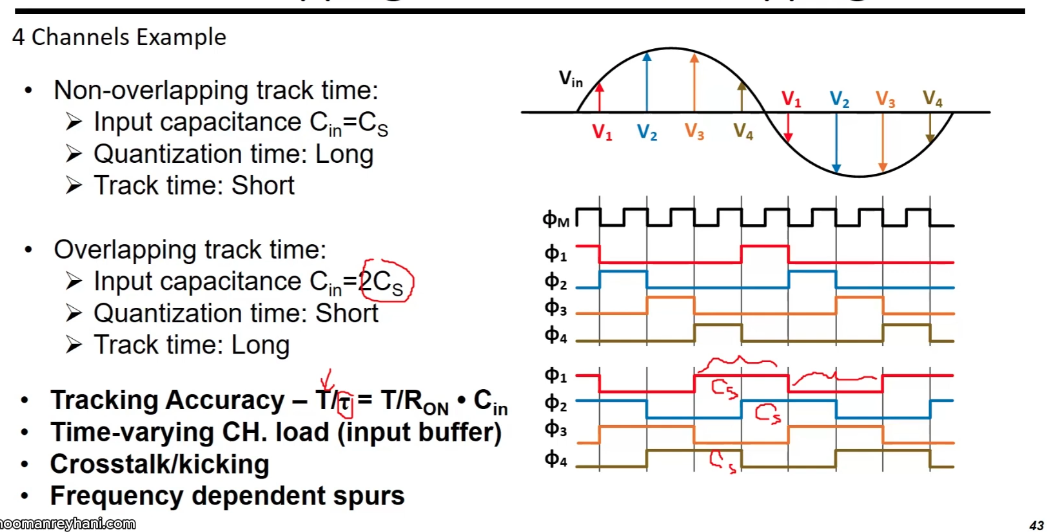
image-20250611224418950

tracking accuracy stay same, Cin (2Cs) counteract the longer tracking

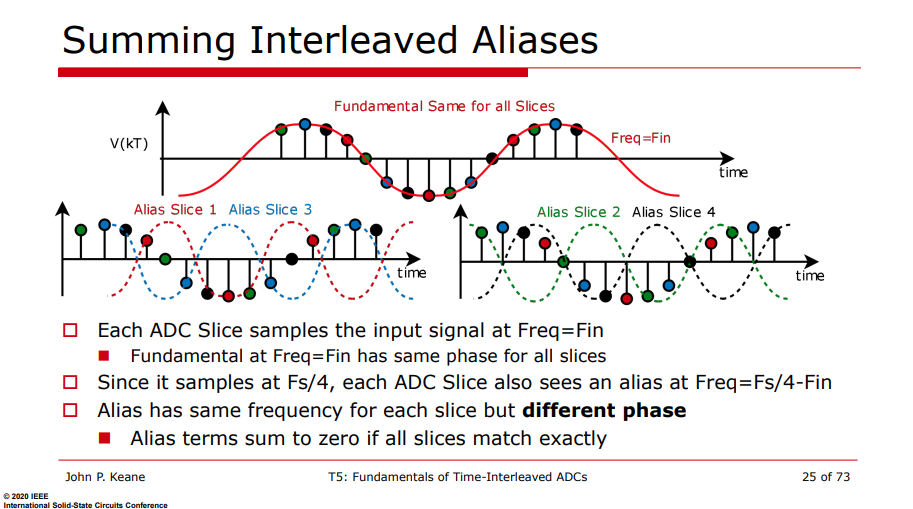
Summing Interleaved Alias

image-20240929215841300

The sampling function - impulse train is \[ s(t) = \sum_{n=-\infty}^{\infty}\left[ \delta(t-n4T_s) + \delta(t-n4T_s-T_s) + \delta(t-n4T_s-2T_s) + \delta(t-n4T_s-3T_s)\right] \]

Its Fourier transform is \[\begin{align} S(f) &= \frac{2\pi}{4T}\sum_{k=-\infty}^{\infty}\left[\delta(f-k\frac{f_s}{4}) + e^{-j2\pi f\cdot T_s}\delta(f-k\frac{f_s}{4}) + e^{-j2\pi f\cdot 2T_s}\delta(f-k\frac{f_s}{4}) + e^{-j2\pi f\cdot 3T_s}\delta(f-k\frac{f_s}{4}) \right] \\ &= \frac{2\pi}{4T}\sum_{k=-\infty}^{\infty}\left(1+e^{-j2\pi\frac{f}{f_s}} + e^{-j4\pi\frac{f}{f_s}} + e^{-j6\pi\frac{f}{f_s}} \right) \delta(f-k\frac{f_s}{4}) \\ &= \frac{2\pi}{4T}\sum_{k=-\infty}^{\infty}\left(1+e^{-jk\frac{\pi}{2}} + e^{-jk\pi} + e^{-jk\frac{3\pi}{2}} \right) \delta(f-k\frac{f_s}{4}) \end{align}\]

We define \(M[k] = 1+e^{-jk\frac{\pi}{2}} + e^{-jk\pi} + e^{-jk\frac{3\pi}{2}}\), which is periodic, i.e. \(M[k]=M[k+4]\) \[ M[k]=\left\{ \begin{array}{cl} 4 & : \ k = 4m \\ 0 & : \ k=4m+1 \\ 0 & : \ k=4m+2 \\ 0 & : \ k=4m+3 \\ \end{array} \right. \]

That is \[ S(f) = \frac{2\pi}{T}\sum_{k=-\infty}^{\infty} \delta(f-kf_s) \]

Alias has same frequency for each slice but different phase: Alias terms sum to zero if all slices match exactly

Random Chopping in TI-ADC

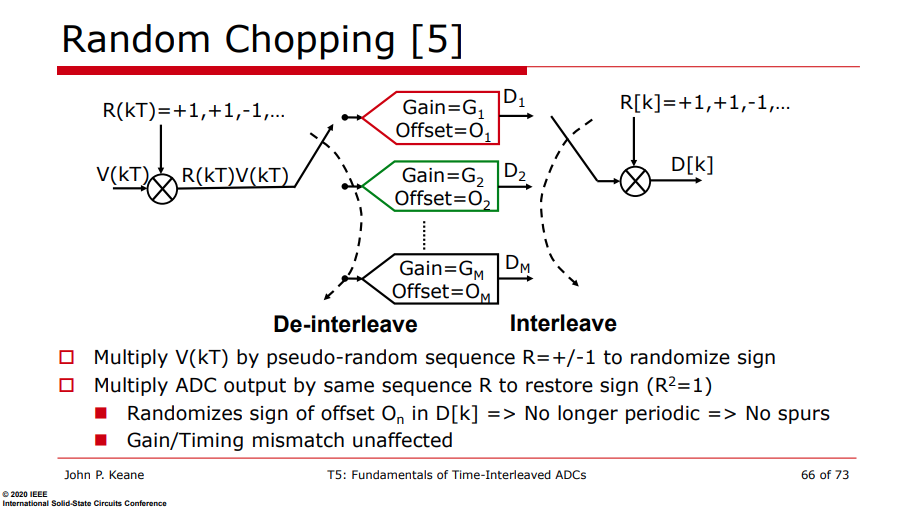
image-20240929215927957

\[ D_n(kT) = (G_n R(kT) V(kT) + O_n)R(kT)= C_n V(kT) + R(kT)O_n \]

ADC buffers & memory effect

Y. Shifman, Y. Krupnik, U. Virobnik, A. Khairi, Y. Sanhedrai and A. Cohen, "A 1.64mW Differential Super Source-Follower Buffer with 9.7GHz BW and 43dB PSRR for Time-Interleaved ADC Applications in 10nm," 2019 IEEE Asian Solid-State Circuits Conference (A-SSCC), Macau, Macao, 2019 [pdf]

E. -H. Chen et al., "7.1 A 212.5Gb/s DSP-Based PAM-4 Transceiver with 50dB Loss Compensation for Large AI System Interconnects in 4nm FinFET," 2025 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 2025

TODO 📅

Paper from industry

Z. Guo et al., "A 112.5Gb/s ADC-DSP-Based PAM-4 Long-Reach Transceiver with >50dB Channel Loss in 5nm FinFET," 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 2022 [https://sci-hub.st/10.1109/ISSCC42614.2022.9731650]

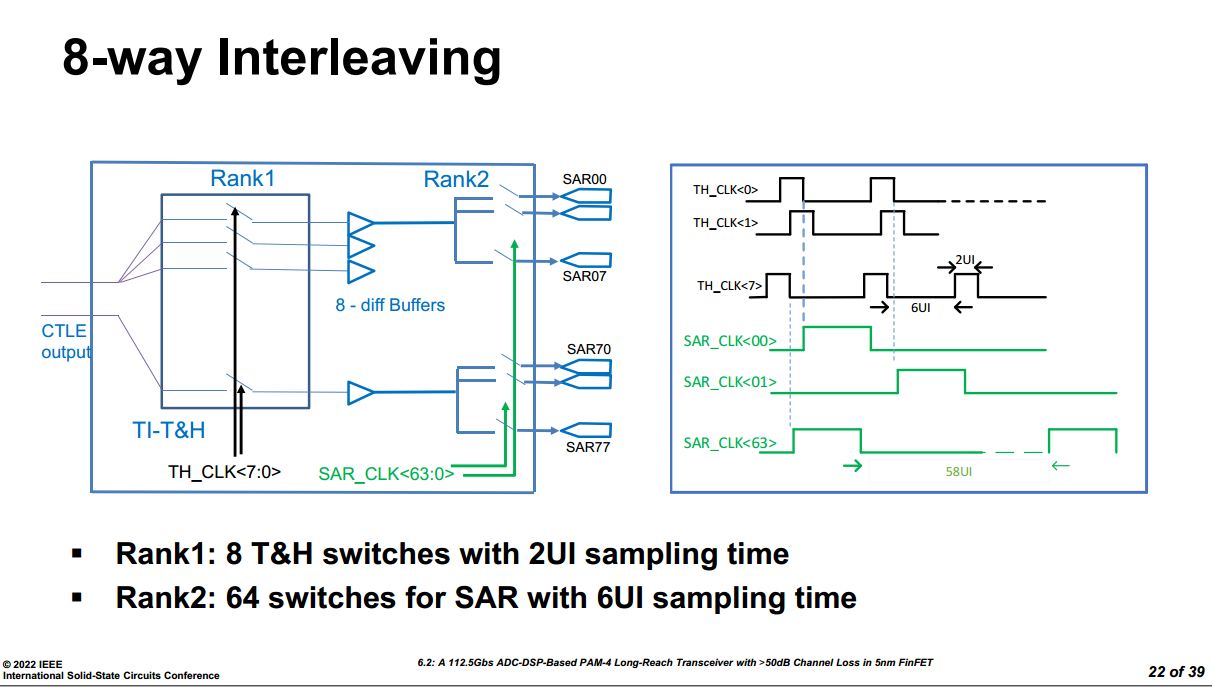
image-20250806224145281

8way-interleaving-Marvell-ISSCC2022.drawio

P. Liu et al., "A 128Gb/s ADC/DAC Based PAM-4 Transceiver with >45dB Reach in 3nm FinFET," 2025 Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Kyoto, Japan, 2025

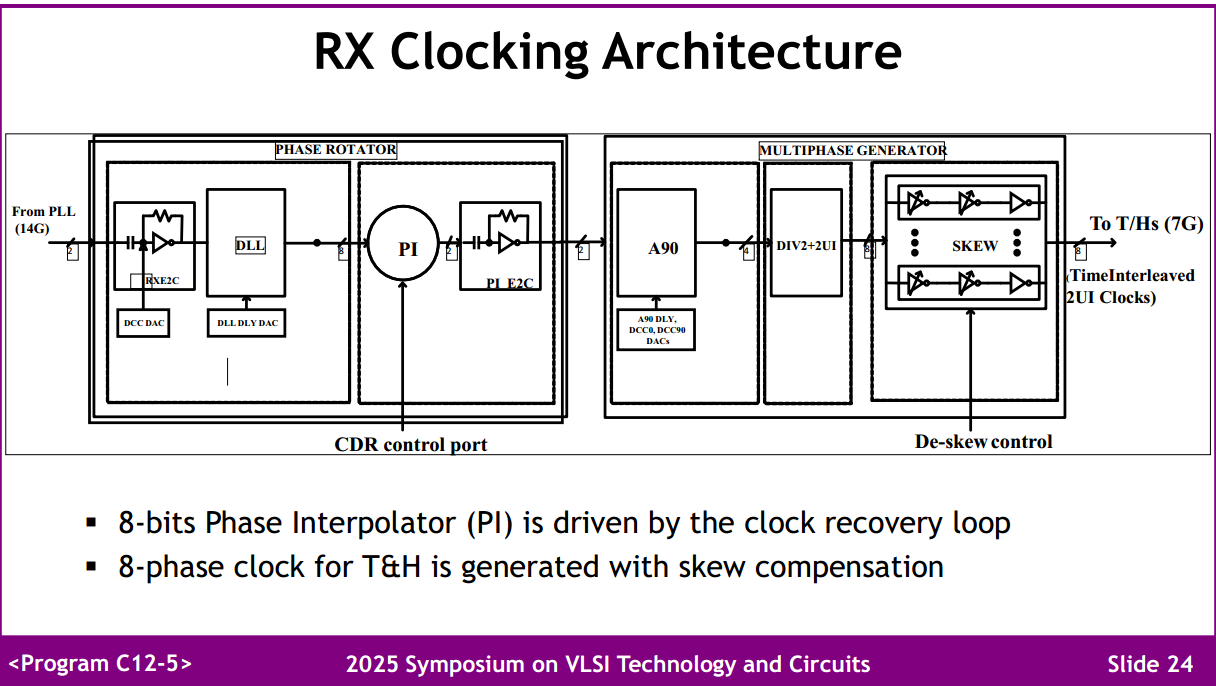
image-20250808220954208

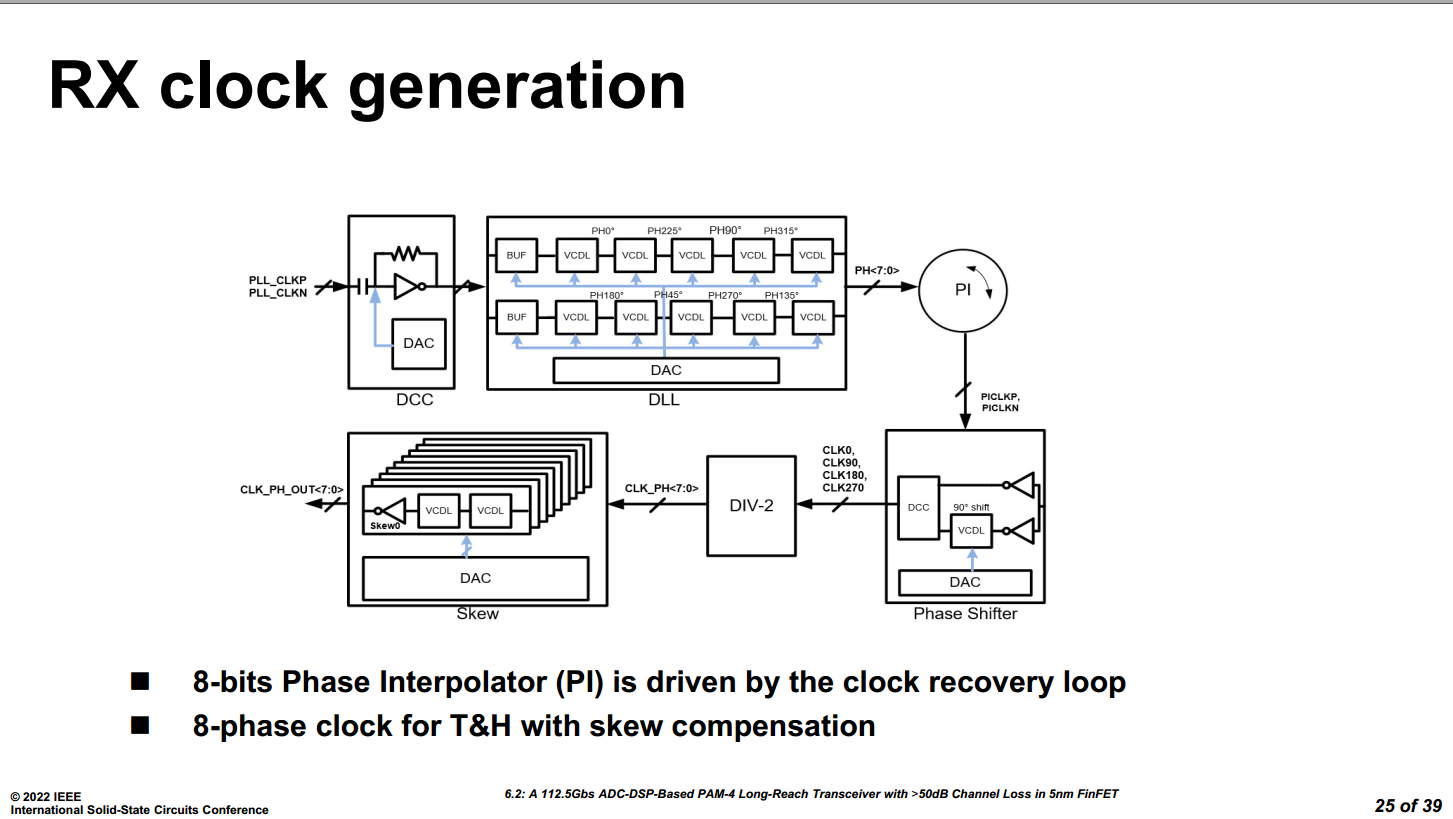
image-20250808221134749

RX-Clocking-Marvell-VLSI2025.drawio

ISSCC.2024 7.3 A 224Gbs 3pJb 40dB Insertion Loss Transceiver in 3nm FinFET CMOS [7.3 A 224Gbs 3pJb 40dB Insertion Loss Transceiver in 3nm FinFET CMOS https://www.bilibili.com/video/BV18hYCe7E45/?share_source=copy_web&vd_source=5a095c2d604a5d4392ea78fa2bbc7249]

ISSCC.2018 6.4 A Fully Adaptive 19-to-56Gb/s PAM-4 Wireline Transceiver with a Configurable ADC in 16nm FinFET [https://sci-hub.st/10.1109/ISSCC.2018.8310207]

M. S. Jalali, A. Sheikholeslami, M. Kibune and H. Tamura, "A Reference-Less Single-Loop Half-Rate Binary CDR," in IEEE Journal of Solid-State Circuits, vol. 50, no. 9, pp. 2037-2047, Sept. 2015 [https://www.eecg.utoronto.ca/~ali/papers/jssc2015-09.pdf]

Pisati, et.al., "Sub-250mW 1-to-56Gb/s Continuous-Range PAM-4 42.5dB IL ADC/DAC- Based Transceiver in 7nm FinFET," 2019 IEEE International Solid-State Circuits Conference (ISSCC), 2019 [https://sci-hub.se/10.1109/ISSCC.2019.8662428]

reference

John P. Keane, ISSCC2020 T5: "Fundamentals of Time-Interleaved ADCs" [https://www.nishanchettri.com/isscc-slides/2020%20ISSCC/TUTORIALS/T5Visuals.pdf]

Yohan Frans, CICC2019 ES3-3- "ADC-based Wireline Transceivers" [pdf]

Samuel Palermo, ISSCC 2018 T10: ADC-Based Serial Links: Design and Analysis [https://www.nishanchettri.com/isscc-slides/2018%20ISSCC/TUTORIALS/T10/T10Visuals.pdf]

ISSCC2015 F1: High-Speed Interleaved ADCs [https://picture.iczhiku.com/resource/eetop/wykrheUfrWasiMVX.pdf]

Poulton, Ken. ISSCC2009 "Time-Interleaved ADCs, Past and Future" (slides)

—. CICC2010 "GHz ADCs: From Exotic to Mainstream", tutorial session, (slides)

—. ISSCC2015 "Interleaved ADCs Through the Ages", (slides)

Ewout Martens. ESSCIRC 2019 Tutorials: Advanced Techniques for ADCs for 5G Massive MIMO [https://youtu.be/7hYichGGU6k]

Athanasios Ramkaj. January 26, 2022, IEEE SSCS Santa Clara Valley Section Technical Talk: Design Considerations Towards Optimal High-Resolution Wide-Bandwidth Time-Interleaved ADCs [https://youtu.be/k3jY9NtfYlY?si=K9AdT9QzGxOnI5WG]

Ahmed M. A. Ali 2016, "High Speed Data Converters" [pdf]

S. Jang, J. Lee, Y. Choi, D. Kim, and G. Kim, "Recent advances in ultra-high-speed wireline receivers with ADC-DSP-based equalizers," IEEE Open Journal of the Solid-State Circuits Society (OJ-SSCS), vol. 4, pp. 290-304, Nov. 2024.

Yida Duan. Design Techniques for Ultra-High-Speed Time-Interleaved Analog-to-Digital Converters (ADCs) [http://www2.eecs.berkeley.edu/Pubs/TechRpts/2017/EECS-2017-10.pdf]

Preview Lecture #1 - "Extreme SAR ADCs" Online Course (2024) - Prof. Chi-Hang Chan (U. of Macau) [https://youtu.be/rgMRL4QZ-wA]