Wireline Transmitter
1UI Data Staggering
TODO 📅
1UI Pulse Generator
duty correction & delay adjustment
TODO 📅
DAC Driver SNDR
TODO 📅
Eye Linearity vs. RLM (Relative Level Mismatch)
TODO 📅
Chaowaroj (Max) Wanotayaroj. Introduction to PAM4 [https://indico.cern.ch/event/979659/contributions/4127016/attachments/2159338/3642883/PAM4Eval%20-%20Dec2020%20Seminar.pdf]
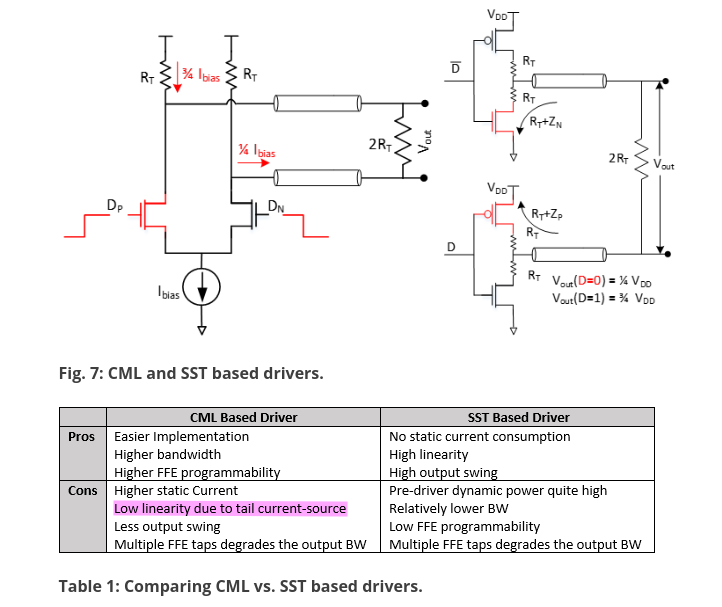
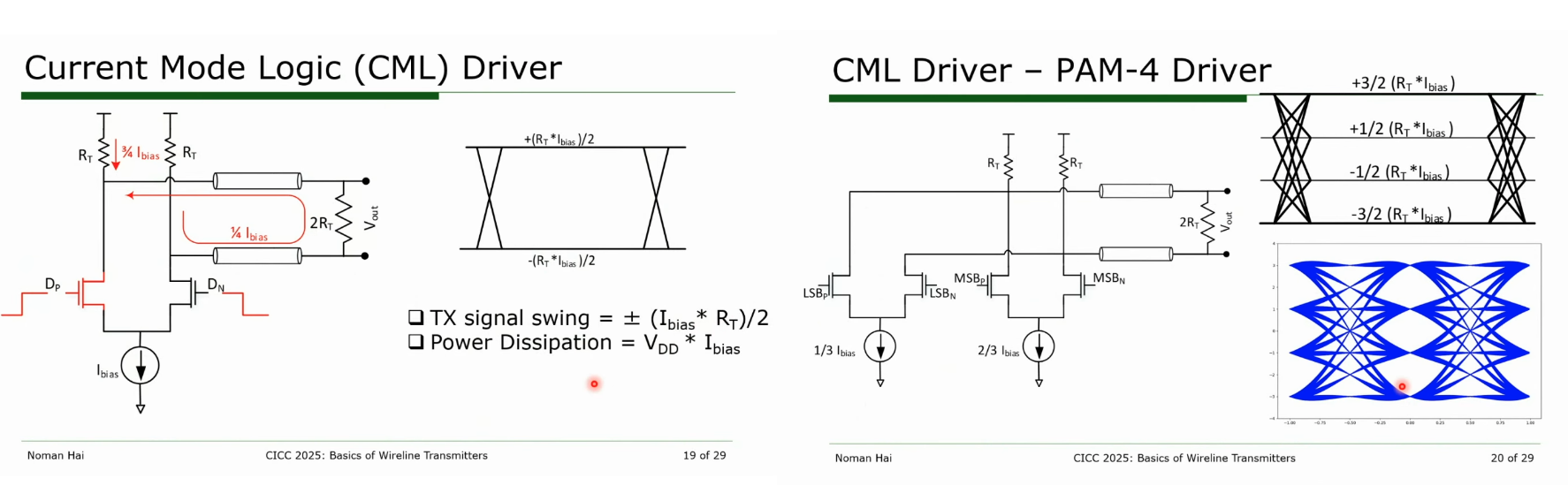
CML vs. SST based driver
Design Challenges Of High-Speed Wireline Transmitters [https://semiengineering.com/design-challenges-of-high-speed-wireline-transmitters/]
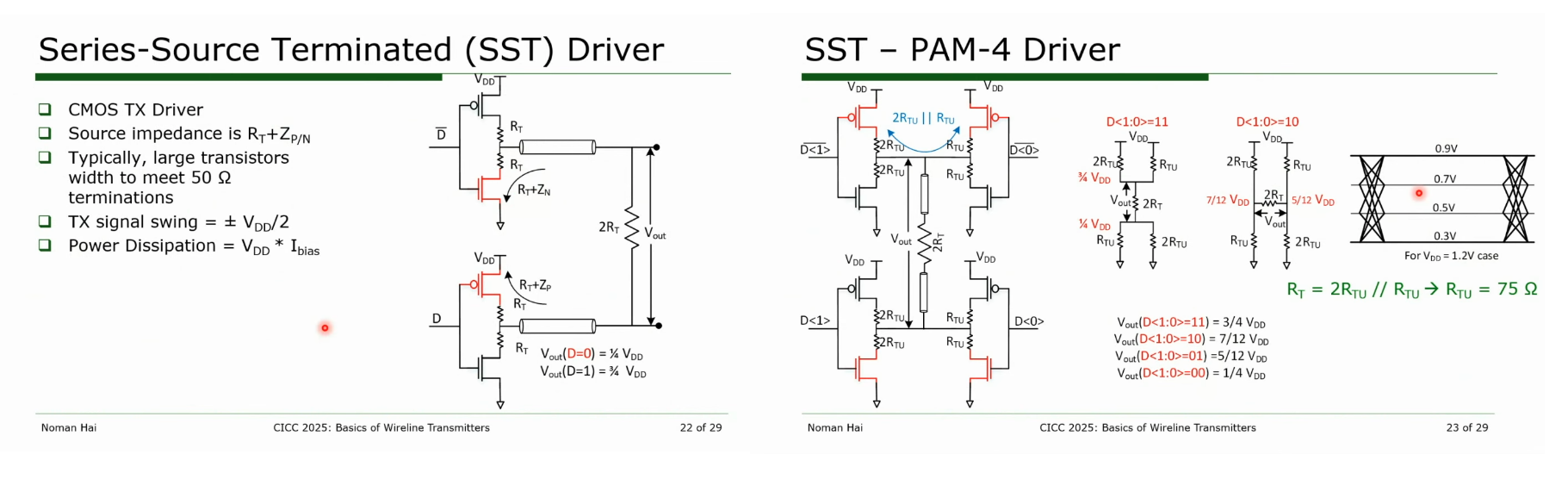
the resistance of MOS is not highly controlled -> \(R_T + Z_N\)
Peak power constraint of TX FIR
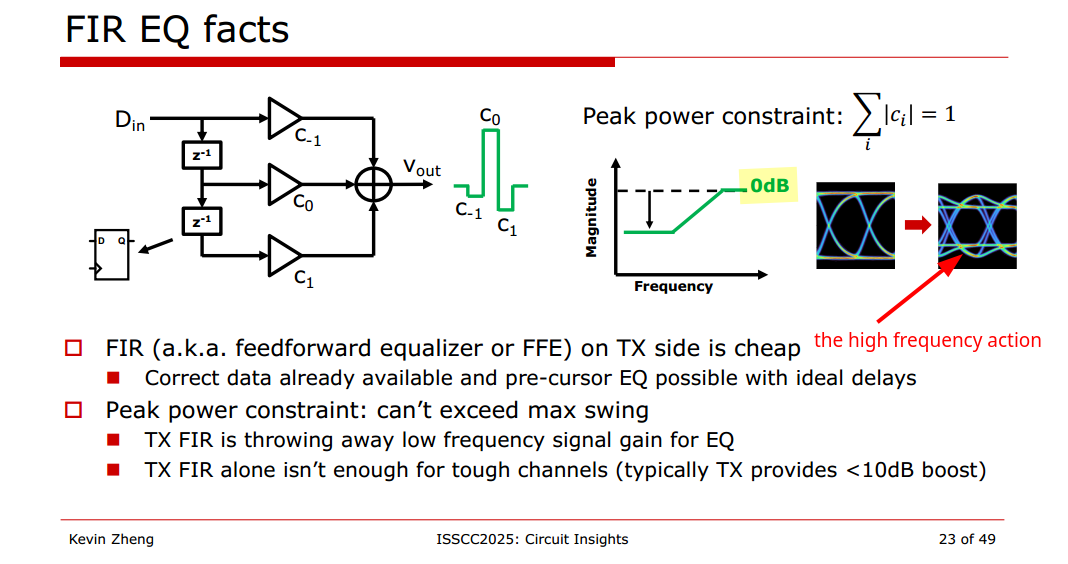
Due to circuit limitation, circuit cannot have arbitrarily large voltage on the output, i.e. a limited maximum swing. In order to create the high frequency shape, the best we can do is lower DC gain (low frequency gain < 1)
- FIR is not increasing the amplitude on the edges
- FIR is reducing the inner eye diagram
The maximum swing stays the same, \(\sum_i |c_i|=1\)
Circuit Insights @ ISSCC2025: Circuits for Wireline Communications - Kevin Zheng [https://youtu.be/8NZl81Dj45M?si=2a8FdfGNP6yBgIW8&t=829]
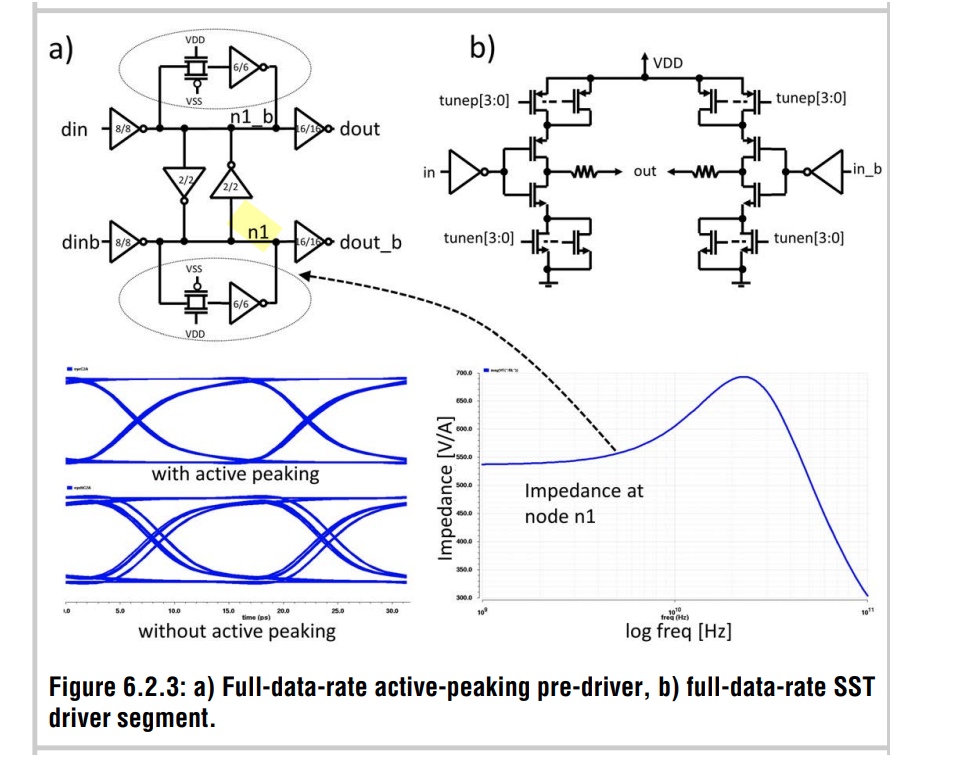
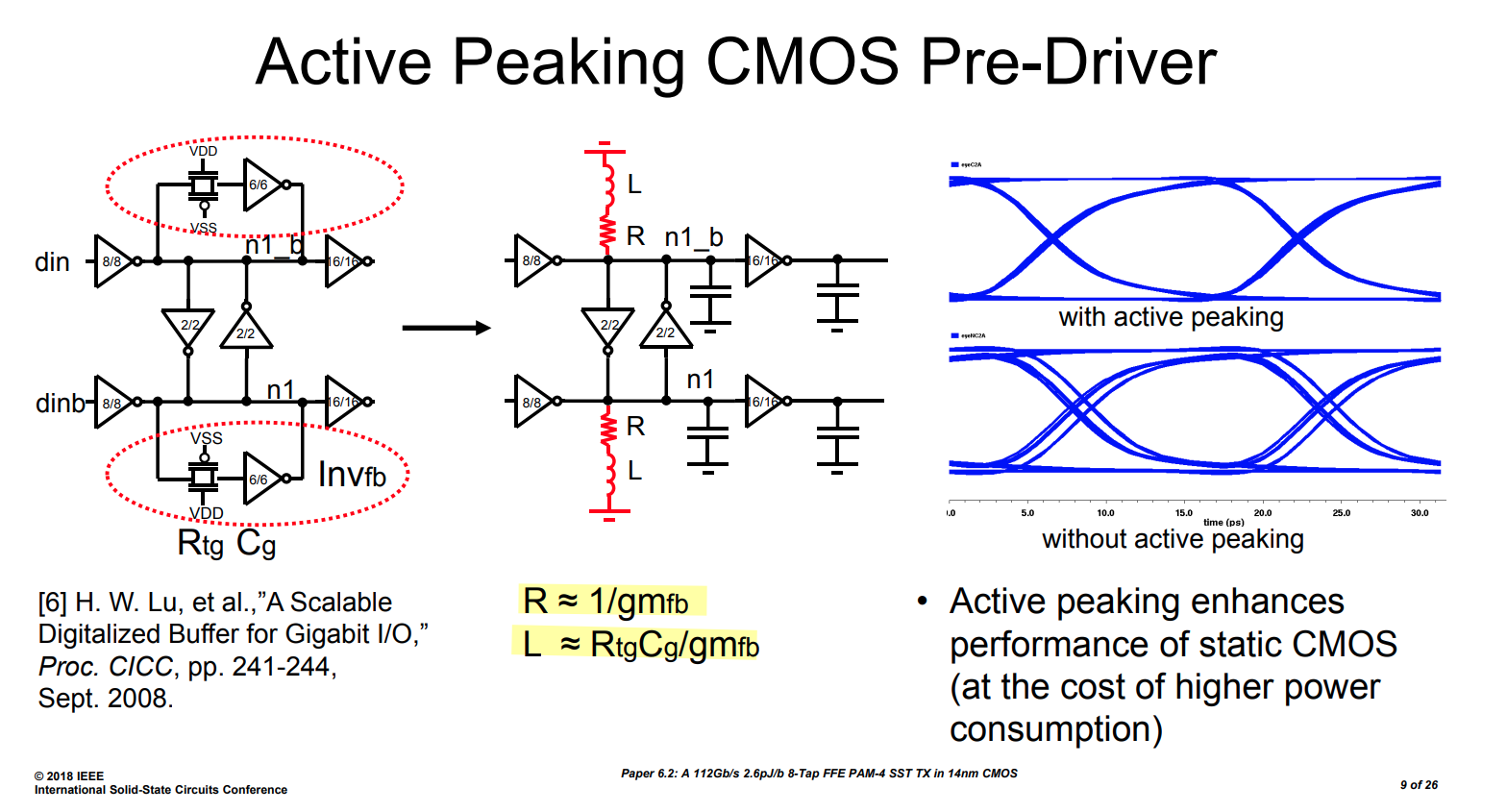
Active Peaking CMOS Pre-Driver
C. Menolfi et al., "A 112Gb/S 2.6pJ/b 8-Tap FFE PAM-4 SST TX in 14nm CMOS," 2018 IEEE International Solid-State Circuits Conference - (ISSCC), San Francisco, CA, USA, 2018, pp. 104-106 [slides paper]
SST Driver
sharing termination in SST transmitter
Sharing termination keep a constant current through leg, which improve TX speed in this way. On the other hand, the sharing termination facilitate drain/source sharing technique in layout.
pull-up and pull-down resistor
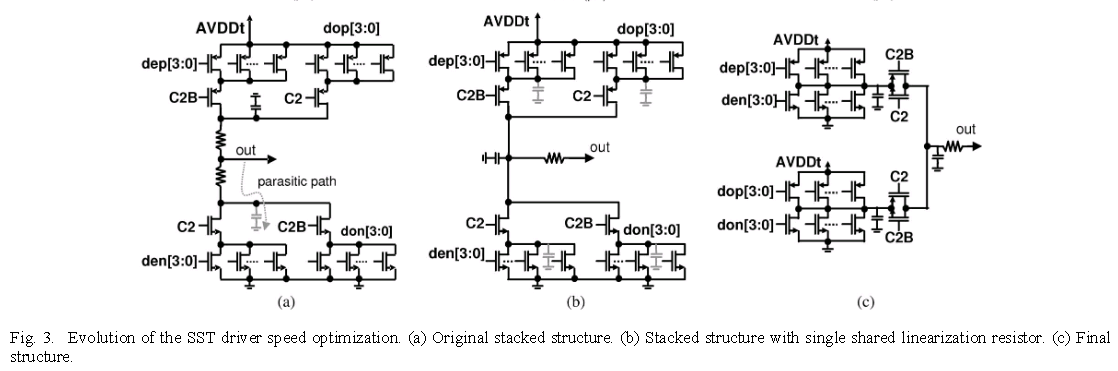
Original stacked structure
Pro's:
smaller static current when both pull up and pull down path is on
Con's:
slowly switching due to parasitic capacitance behind pull-up and pull-down resistor
with single shared linearization resistor
Pro's:
The parasitic capacitance behind the resistor still exists but is now always driven high or low actively
Con's:
more static current
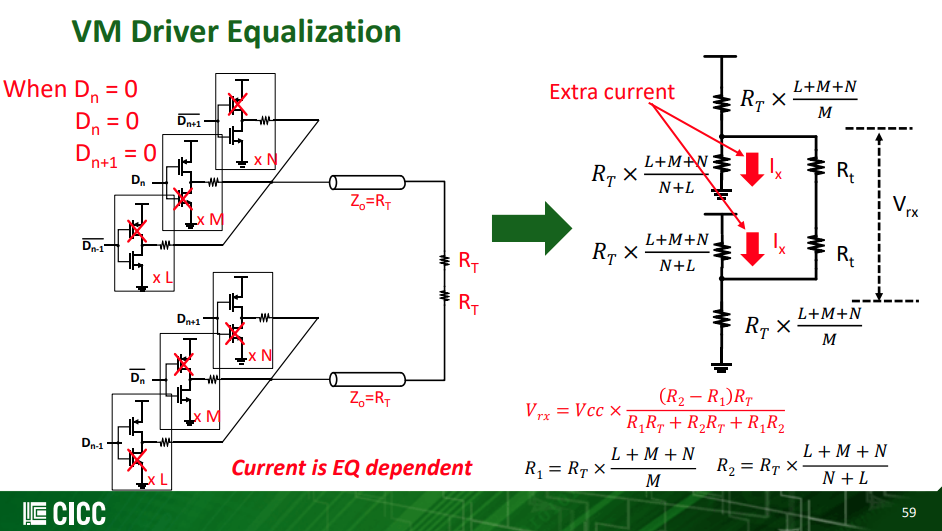
VM Driver Equalization - differential ended termination
\[ V_o = D_{n+1}C_{-1}+D_nC_0+D_{n-1}C_{+1} \]
where \(D_n \in \{-1, 1\}\)
\[
V_{\text{rx}} = V_{\text{dd}} \frac{(R_2-R_1)R_T}{R_1R_T+R_2R_T+R_1R_2}
\] With \(R_u=(L+M+N)R_T\)
Normalize above equation, obtain \[ V_{\text{rx,norm}} = \frac{(R_2-R_1)R_T}{R_1R_T+R_2R_T+R_1R_2} \]
| \(D_{n-1}\) | \(D_{n}\) | \(D_{n+1}\) | |
|---|---|---|---|
| \(C_{-1}\) | 1 | -1 | -1 |
| \(C_0\) | -1 | 1 | -1 |
| \(C_{+1}\) | -1 | -1 | 1 |
Where precursor \(R_L = L\times R_T\), main cursor \(R_M = M\times R_T\) and post cursor \(R_N = N\times R_T\)
Equation-1
\(D_{n-1}D_nD_{n+1}=1,-1,-1\)
\[\begin{align} R_1 &= R_N \\ &= \frac{R_u}{N} \\ R_2 &= R_L\parallel R_M \\ &= \frac{R_u}{L+M} \end{align}\]
We obtain \[ V_{L}= \frac{1}{2}\cdot\frac{N-(L+M)}{L+M+N} \]
Equation-2
\(D_{n-1}D_nD_{n+1}=-1,1,-1\)
with \(R_1=R_T\) and \(R_2=+\infty\), we obtain \[ V_M = \frac{1}{2} \]
Equation-3
\(D_{n-1}D_nD_{n+1}=-1,-1,1\)
\[\begin{align} R_1 &= R_L \\ &= \frac{R_u}{L} \\ R_2 &= R_N\parallel R_M \\ &= \frac{R_u}{N+M} \end{align}\]
We obtain \[ V_N = \frac{1}{2}\cdot\frac{L-(N+M)}{L+M+N} \]
Obtain FIR coefficients
We define \[\begin{align} l &= \frac{L}{L+M+N} \\ m &= \frac{M}{L+M+N} \\ n &= \frac{N}{L+M+N} \end{align}\]
where \(l+m+n=1\)
Due to Eq1 ~ Eq3 \[ \left\{ \begin{array}{cl} C_{-1}-C_0-C_1 & = \frac{1}{2}(n-l-m) \\ -C_{-1}+C_0-C_1 & = \frac{1}{2} \\ -C_{-1}-C_0+C_1 & = \frac{1}{2}(l-n-m) \end{array} \right. \] After scaling, we get \[ \left\{ \begin{array}{cl} C_{-1}-C_0-C_1 & = -l-m+n \\ -C_{-1}+C_0-C_1 & = l+m+n \\ -C_{-1}-C_0+C_1 & = l-m-n \end{array} \right. \] Then, the relationship between FIR coefficients and legs is clear, i.e. \[\begin{align} C_{-1} &= -\frac{L}{L+M+N} \\ C_{0} &= \frac{M}{L+M+N} \\ C_{1} &= -\frac{N}{L+M+N} \end{align}\]
For example, \(C_{-1}=-0.1\), \(C_0=0.7\) and \(C_1=-0.2\) \[
H(z) = -0.1+0.7z^{-1}-0.2z^{-2}
\] 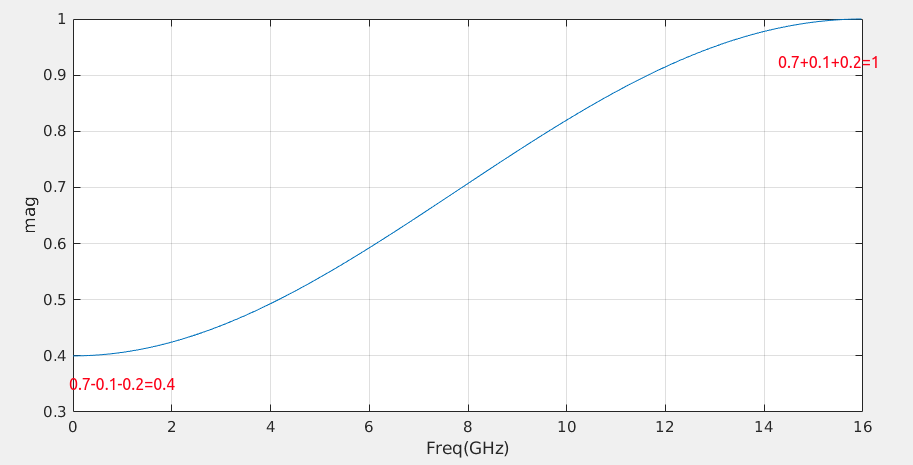
1 | w = [-0.1, 0.7, -0.2]; |
VM Driver Equalization - single ended termination
Equation-1
\[\begin{align} V_{\text{rxp}} &= \frac{1}{2} \cdot \frac{N}{L+M+N} \\ V_{\text{rxm}} &= \frac{1}{2} \cdot \frac{L+M}{L+M+N} \end{align}\] So \[ V_{L}= \frac{1}{2}\cdot\frac{N-(L+M)}{L+M+N} \] which is same with differential ended termination
Equation-2
\[\begin{align} V_{\text{rxp}} &= \frac{1}{2} \\ V_{\text{rxm}} &= 0 \end{align}\] So \[ V_{M}= \frac{1}{2} \] which is same with differential ended termination
Equation-3
\[ V_{N}= \frac{1}{2}\cdot\frac{L-(N+M)}{L+M+N} \]
Obtain FIR coefficients
Same with differential ended termination driver.
Basic Feed Forward Equalization Theory
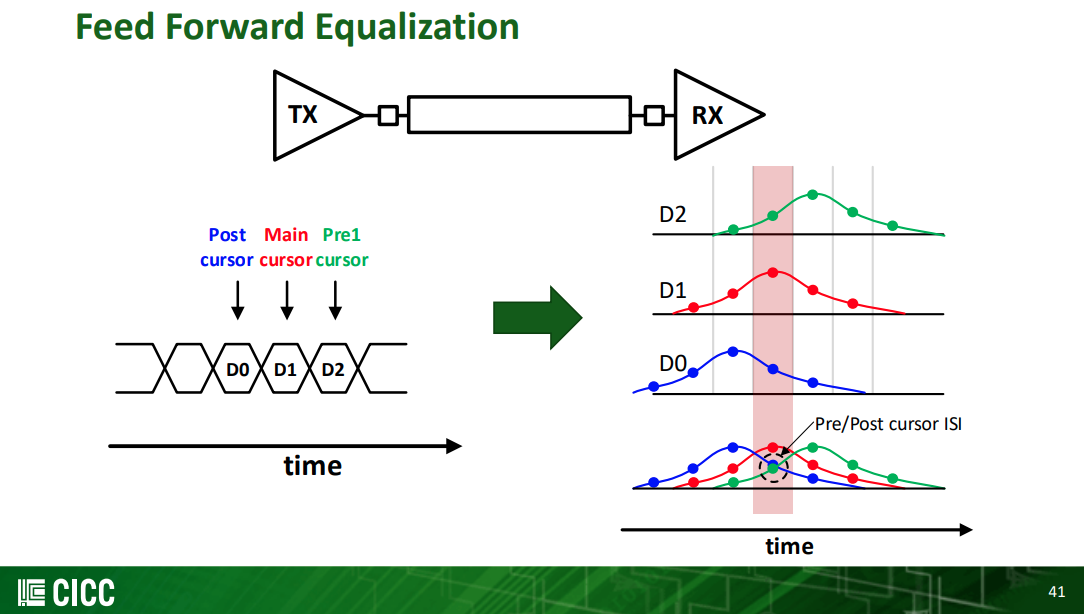
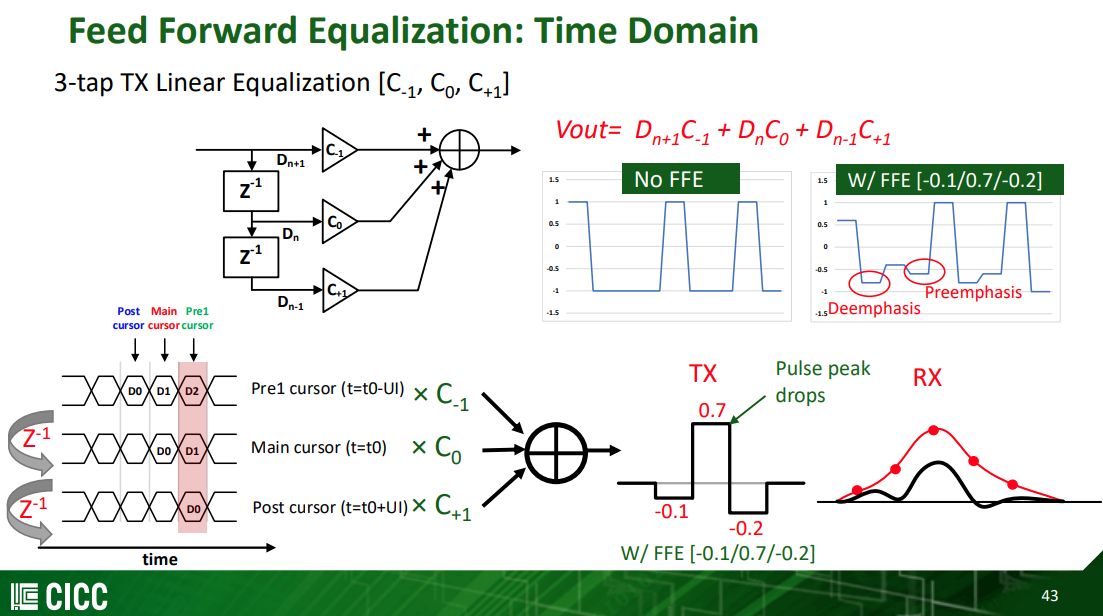
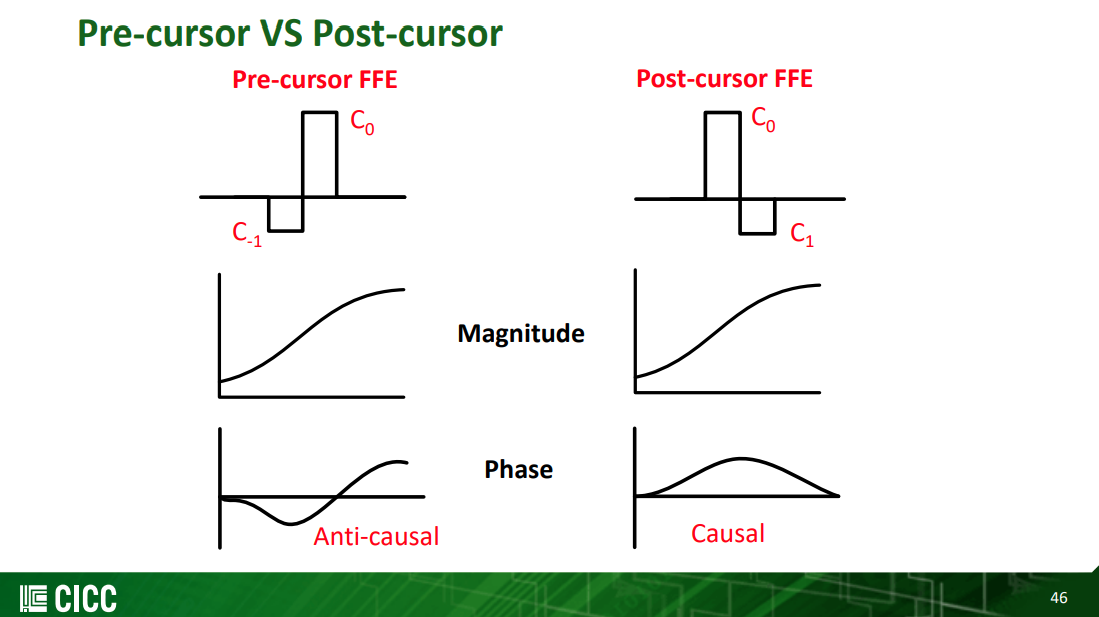
Pre-cursor FFE can compensate phase distortion through the channel
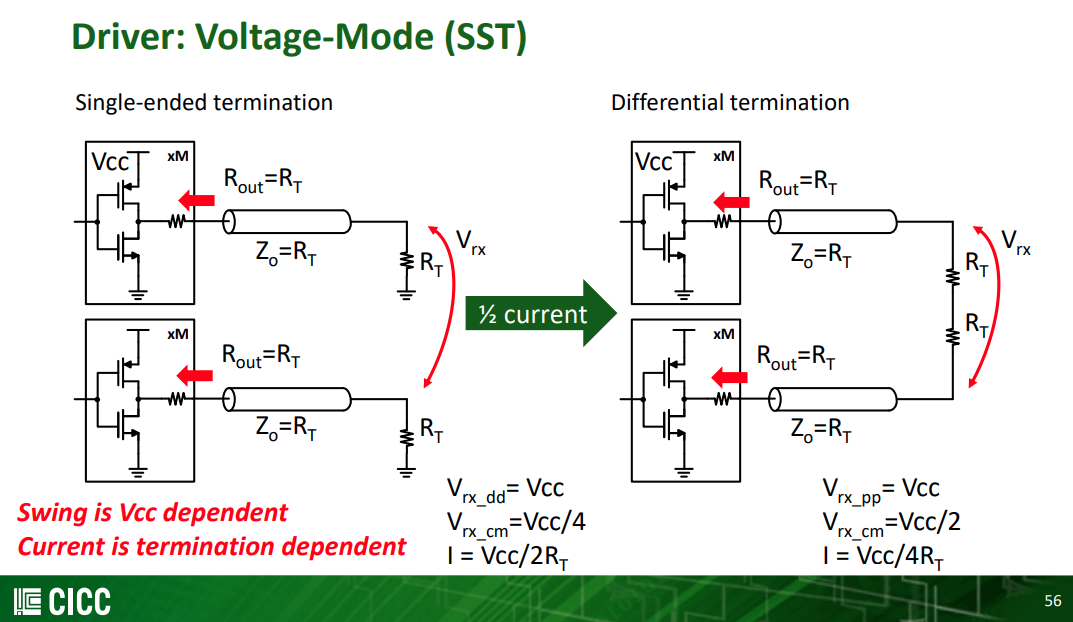
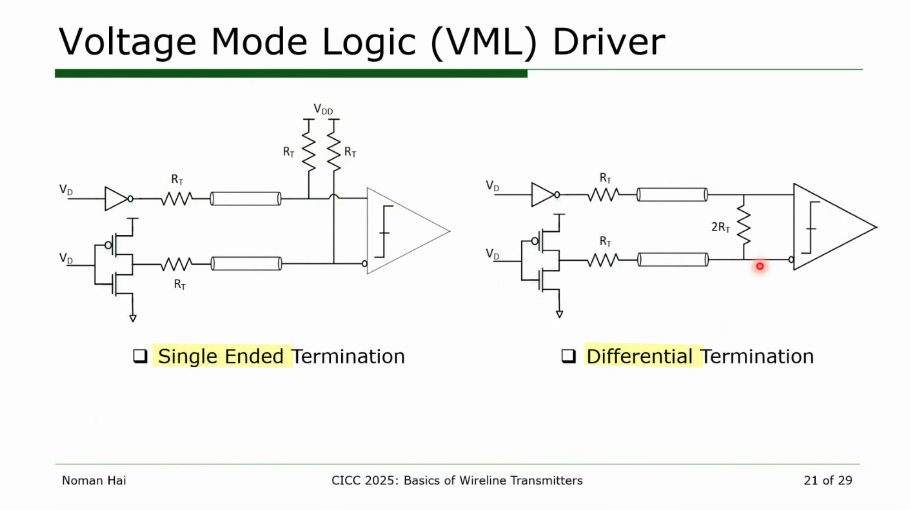
Single-ended termination
Differential termination
TX Serializer
mux timing
divider latch timing
Two latches
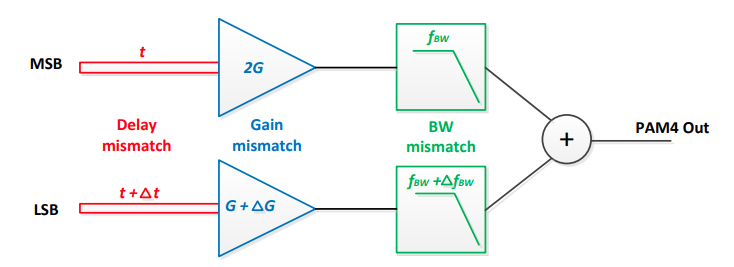
PAM4 TX
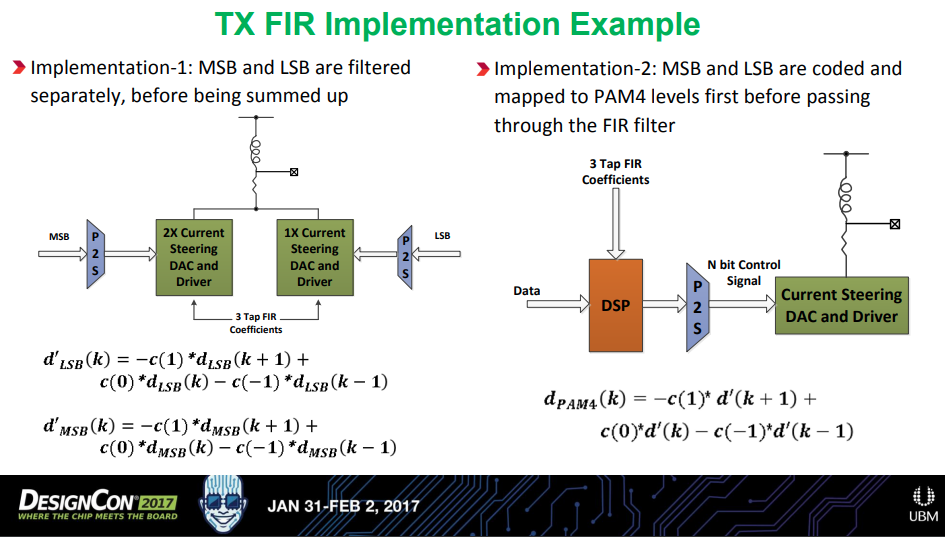
Here, \(d_{\text{LSB}} \in \{-1, 1\}\), \(d_{\text{MSB}} \in \{-2, 2\}\) and \(d' \in \{ -3, -1, 1, 3 \}\)
Implementation-1 could potentially experience performance degradation due to
- Clock skew, \(\Delta t\), could make the eye misaligned horizontally
- Gain mismatch, \(\Delta G\), could cause eye nonlinearity
- Bandwidth mismatch, \(\Delta f_{\text{BW}}\), could make the eye misaligned vertically
Typically, a 3-tap FIR (pre + main + post) TX de-emphasis is used
3-tap FIR results in \(4^3 = 64\) possible distinct signal levels
\[\begin{align} R_U^M \parallel R_D^M &= \frac{3R_T}{2}\\ R_U^L \parallel R_D^L &= 3R_T \end{align}\]
Thevenin Equivalent Circuit is
Which can be simpified as
\[\begin{align}
V_{\text{rx}} &= \frac{1}{2}(V_p - V_m) \\
&= \frac{1}{2}(\frac{2}{3}(2V_{\text{MSB}}+V_{\text{LSB}})-1) \\
&=\frac{1}{3}(2V_{\text{MSB}}+V_{\text{LSB}})-\frac{1}{2}
\end{align}\]
The above eqations demonstrate that the output \(V_{\text{rx}}\) is the linear sum of MSB and LSB; LSB and MSB have relative weight, i.e. 1 for LSB and 2 for MSB.
Assume pre cusor has \(L\) legs, main cursor \(M\) legs and post cursor \(N\) legs, which is same with the convention in "Voltage-Mode Driver Equalization"
The number of legs connected with supply can expressed as \[ n_{up} = (1-d_{n+1})L + d_{n}M + (1-d_{n-1})N \] Where \(d_n \in \{0, 1\}\), or \[ n_{up} = \frac{1}{2}(-D_{n+1}+1)L + \frac{1}{2}(D_{n}+1)M + \frac{1}{2}(-D_{n-1}+1)N \] Where \(D_n \in \{-1, +1\}\)
Then the number of legs connected with ground is \[ n_{dn}=L+M+N-n_{up} \] where \(n_{up}+n_{dn}=L+M+N\)
Voltage resistor divider \[\begin{align} V_o &= \frac{\frac{R_{U}}{n_{dn}}}{\frac{R_U}{n_{dn}}+\frac{R_U}{n_{up}}} \\ &= \frac{1}{2}- \frac{1}{2}D_{n+1}\frac{L}{L+M+N}+ \frac{1}{2}D_{n}\frac{M}{L+M+N}-\frac{1}{2}D_{n-1}\frac{N}{L+M+N} \\ &= \frac{1}{2}-\frac{1}{2}D_{n+1}\cdot l+ \frac{1}{2}D_{n}\cdot m-\frac{1}{2}D_{n-1}\cdot n \end{align}\]
where \(l+m+n=1\)
\(V_{\text{MSB}}\) and \(V_{\text{LSB}}\) can be obtained
\[\begin{align} V_{\text{MSB}} &= \frac{1}{2}-\frac{1}{2}D^{\text{MSB}}_{n+1}\cdot l+ \frac{1}{2}D^{\text{MSB}}_{n}\cdot m-\frac{1}{2}D^{\text{MSB}}_{n-1}\cdot n \\ V_{\text{LSB}} &= \frac{1}{2}-\frac{1}{2}D^{\text{LSB}}_{n+1}\cdot l+ \frac{1}{2}D^{\text{LSB}}_{n}\cdot m-\frac{1}{2}D^{\text{LSB}}_{n-1}\cdot n \end{align}\]
Substitute the above equation into \(V_{\text{rx}}\), we obtain the relationship between driver legs and FFE coefficients
\[\begin{align} V_{\text{rx}} &=\frac{1}{3}(2V_{\text{MSB}}+V_{\text{LSB}})-\frac{1}{2} \\ &= \frac{1}{3} \left\{ 2\left( \frac{1}{2}-\frac{1}{2}D^{\text{MSB}}_{n+1}\cdot l+ \frac{1}{2}D^{\text{MSB}}_{n}\cdot m- \frac{1}{2}D^{\text{MSB}}_{n-1}\cdot n \right) + \left( \frac{1}{2}-\frac{1}{2}D^{\text{LSB}}_{n+1}\cdot l+ \frac{1}{2}D^{\text{LSB}}_{n}\cdot m- \frac{1}{2}D^{\text{LSB}}_{n-1}\cdot n \right) \right\}-\frac{1}{2} \\ &= \left(-\frac{l}{6} \cdot 2 \cdot D^{\text{MSB}}_{n+1}+ \frac{m}{6} \cdot 2 \cdot D^{\text{MSB}}_{n}- \frac{n}{6} \cdot 2 \cdot D^{\text{MSB}}_{n-1}\right) + \left(-\frac{l}{6} \cdot D^{\text{LSB}}_{n+1}+ \frac{m}{6} \cdot D^{\text{LSB}}_{n}- \frac{n}{6} \cdot D^{\text{LSB}}_{n-1}\right) \\ &= -\frac{l}{6}(2 \cdot D^{\text{MSB}}_{n+1}+D^{\text{LSB}}_{n+1})+ \frac{m}{6}(2\cdot D^{\text{MSB}}_{n}+D^{\text{LSB}}_{n}) -\frac{n}{6}(2\cdot D^{\text{MSB}}_{n-1}+D^{\text{LSB}}_{n-1}) \end{align}\]
After scaling, we obtain \[ V_{\text{rx}} = -l\cdot(2 \cdot D^{\text{MSB}}_{n+1}+D^{\text{LSB}}_{n+1})+ m\cdot(2\cdot D^{\text{MSB}}_{n}+D^{\text{LSB}}_{n}) - n \cdot(2\cdot D^{\text{MSB}}_{n-1}+D^{\text{LSB}}_{n-1}) \] Where \(C_{-1} = l\), \(C_0 = m\) and \(C_{1}=n\), which is same with that of NRZ
Test Challenges
PAM4 Transmitter Test Challenges [https://harrisburg.psu.edu/files/pdf/16861/2019/05/06/tektronix_penn_state_si_april_12_2019.pdf]
PAM4 Signaling in High Speed Serial Technology: Test, Analysis, and Debug [https://download.tek.com/document/55W_60273_1_HR_Letter.pdf]
TODO 📅
reference
Noman Hai, Synopsys. CICC 2025 Circuit Insights: Basics of Wireline Transmitter Circuits [https://youtu.be/oofViBGlrjM?si=WZnOqtDVG3iDnBHI]
—, Synopsys. Design Challenges Of High-Speed Wireline Transmitters [https://semiengineering.com/design-challenges-of-high-speed-wireline-transmitters/]
—, Synopsys. CMOS Circuit Techniques for Wireline Transmitters [https://www.synopsys.com/webinars/wireline-transmitters-part-1.html]
Jihwan Kim, CICC 2022, ES4-4: Transmitter Design for High-speed Serial Data Communications
—, ISSCC2019 F5: Design Techniques for a 112Gbs PAM-4 Transmitter
Friedel Gerfers, ISSCC2021 T6: Basics of DAC-based Wireline Transmitters [https://www.nishanchettri.com/isscc-slides/2021%20ISSCC/TUTORIALS/ISSCC2021-T6.pdf]
Tod Dickson, IBM. High-Speed CMOS Serial Transmitters for 56-112Gb/s Electrical Interconnects [https://www.youtube.com/watch?v=g1pcZabsRNc]
B. Razavi, "Design Techniques for High-Speed Wireline Transmitters," in IEEE Open Journal of the Solid-State Circuits Society, vol. 1, pp. 53-66, 2021, [https://www.seas.ucla.edu/brweb/papers/Journals/BROJSSCSep21.pdf]
Yvain Thonnart, CEA-LIST. ISSCC2021 T8: On-Chip Interconnects: Basic Concepts, Designs and Future Opportunities [https://www.nishanchettri.com/isscc-slides/2021%20ISSCC/TUTORIALS/ISSCC2021-T8.pdf]
Mozhgan Mansuri. ISSCC2021 SC3: Clocking, Clock Distribution, and Clock Management in Wireline/Wireless Subsystems [https://www.nishanchettri.com/isscc-slides/2021%20ISSCC/SHORT%20COURSE/ISSCC2021-SC3.pdf]
Sam Palermo. High-Performance SERDES Design" Online Course (2025): Current-Mode DAC TX [https://youtu.be/A2VsvCPDWxk?si=14J7JC_bnejAlHGW]
PCIe® 6.0 Specification: The Interconnect for I/O Needs of the Future PCI-SIG® Educational Webinar Series, [https://pcisig.com/sites/default/files/files/PCIe%206.0%20Webinar_Final_.pdf]
J. F. Bulzacchelli et al., "A 28-Gb/s 4-Tap FFE/15-Tap DFE Serial Link Transceiver in 32-nm SOI CMOS Technology," in IEEE Journal of Solid-State Circuits, vol. 47, no. 12, pp. 3232-3248, Dec. 2012, doi: 10.1109/JSSC.2012.2216414.
C. Menolfi et al., "A 112Gb/S 2.6pJ/b 8-Tap FFE PAM-4 SST TX in 14nm CMOS," 2018 IEEE International Solid - State Circuits Conference - (ISSCC), 2018, pp. 104-106, doi: 10.1109/ISSCC.2018.8310205.
E. Chong et al., "A 112Gb/s PAM-4, 168Gb/s PAM-8 7bit DAC-Based Transmitter in 7nm FinFET," ESSCIRC 2021 - IEEE 47th European Solid State Circuits Conference (ESSCIRC), 2021, pp. 523-526, doi: 10.1109/ESSCIRC53450.2021.9567801.
Wang, Z., Choi, M., Lee, K., Park, K., Liu, Z., Biswas, A., Han, J., Du, S., & Alon, E. (2022). An Output Bandwidth Optimized 200-Gb/s PAM-4 100-Gb/s NRZ Transmitter With 5-Tap FFE in 28-nm CMOS. IEEE Journal of Solid-State Circuits, 57(1), 21-31. https://doi.org/10.1109/JSSC.2021.3109562
J. Kim et al., "A 112Gb/s PAM-4 transmitter with 3-Tap FFE in 10nm CMOS," 2018 IEEE International Solid - State Circuits Conference - (ISSCC), 2018, pp. 102-104, doi: 10.1109/ISSCC.2018.8310204.