ADC in Instrument & Measurement (I&M)

Posted on Edited on In

image-20250612003115259

Dual Slope ADC

image-20250615153045770

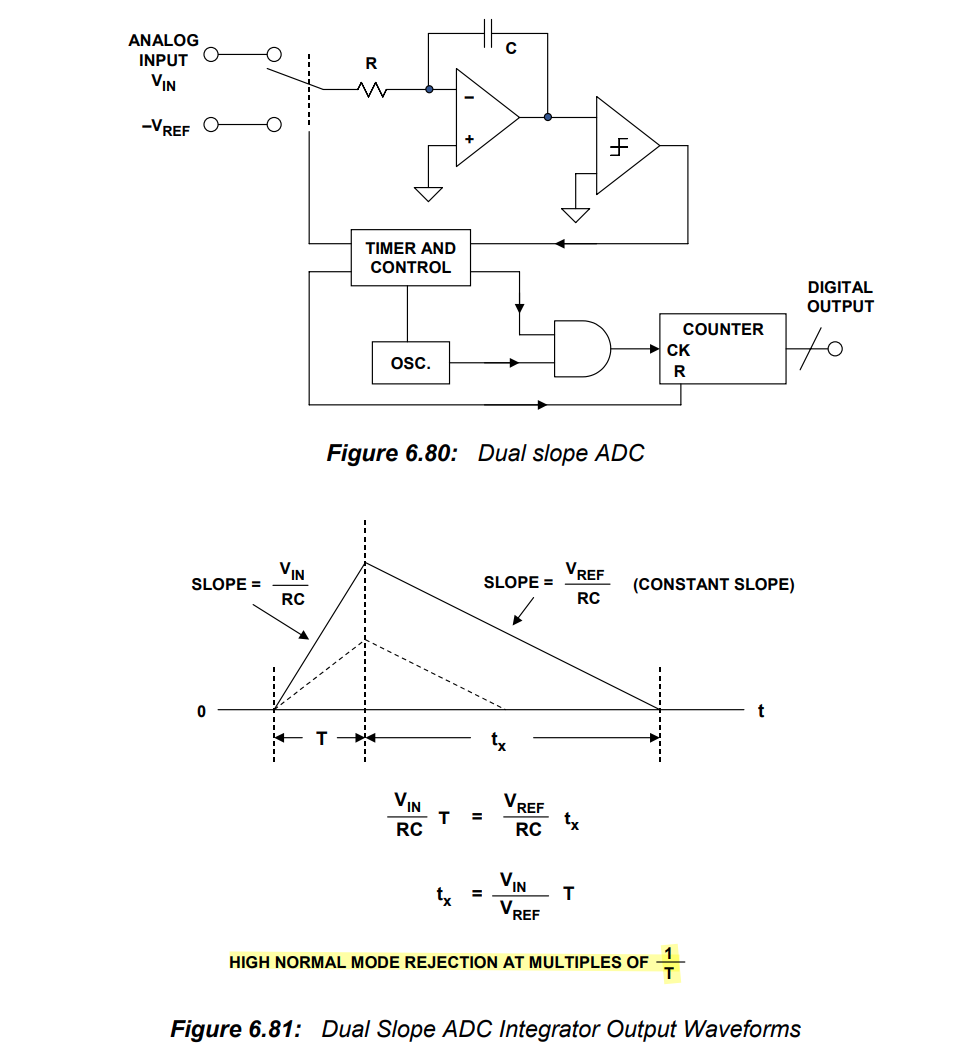
image-20250615152228233

\[ V_{IN} = \frac{V_{REF}}{T}t_\text{x} = \frac{V_{REF}}{2^N}\cdot 2^{N_\text{x}} \]

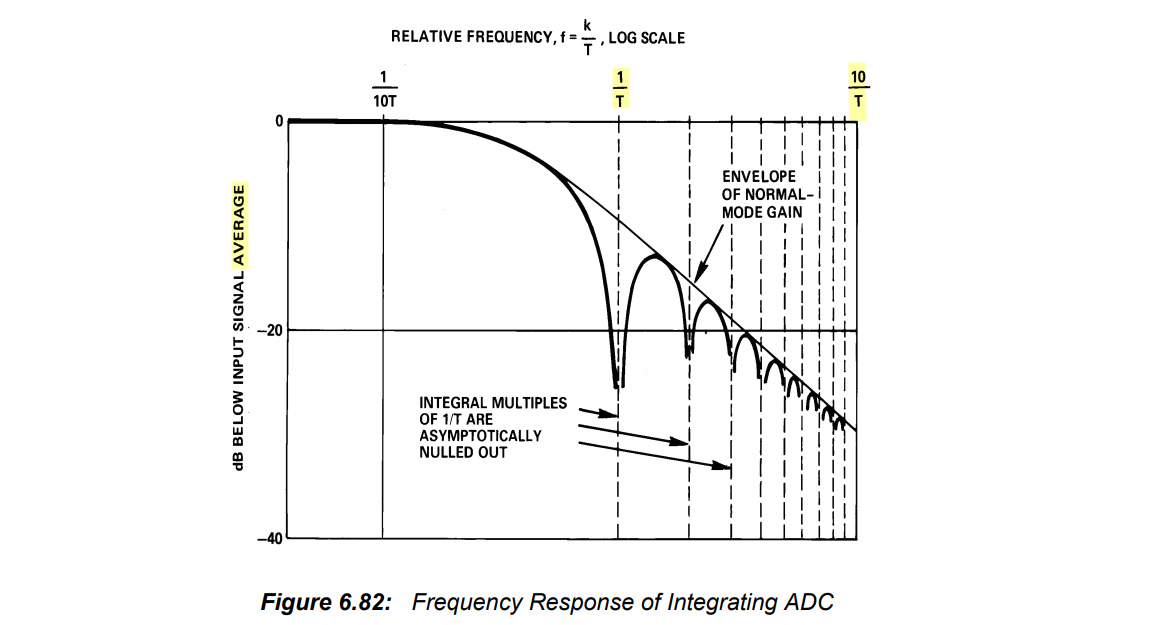
Normal Mode Rejection

a high normal mode rejection ratio (NMRR) for input noise at line frequency

image-20250615160802268

  • Conversion accuracy is independent of both the capacitance and the clock frequency, because they affect both the up-slope and the down-slope by the same ratio

  • The fixed input signal integration period results in rejection of noise frequencies on the analog input that have periods that are equal to or a sub-multiple of the integration time \(T\)

    Interference signals with frequencies at integral multiples of the integration period are, theoretically, completely removed, since the average value of a sine wave of frequency (\(1/T\)) averaged over a period (\(T\)) is zero

image-20250615155921455

Linear Circuit Design Handbook, 2008 [https://www.analog.com/media/en/training-seminars/design-handbooks/Basic-Linear-Design/Chapter6.pdf]

Precision Analog Front Ends with Dual Slope ADC [https://ww1.microchip.com/downloads/aemDocuments/documents/APID/ProductDocuments/DataSheets/21428e.pdf]

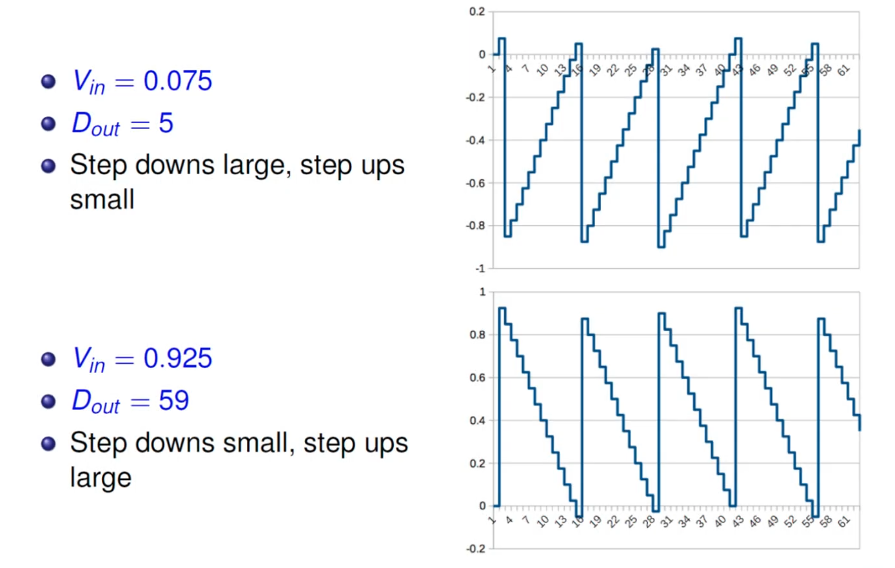
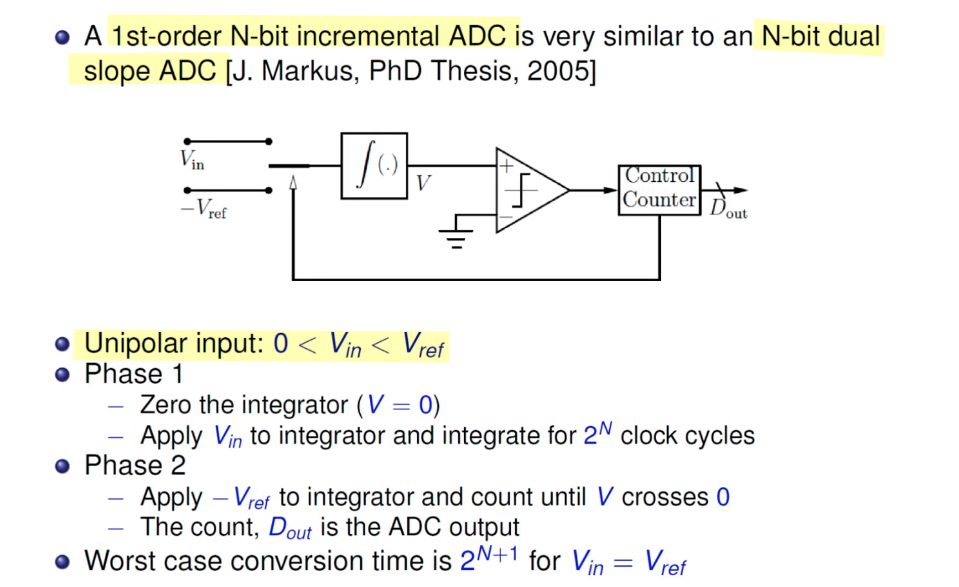
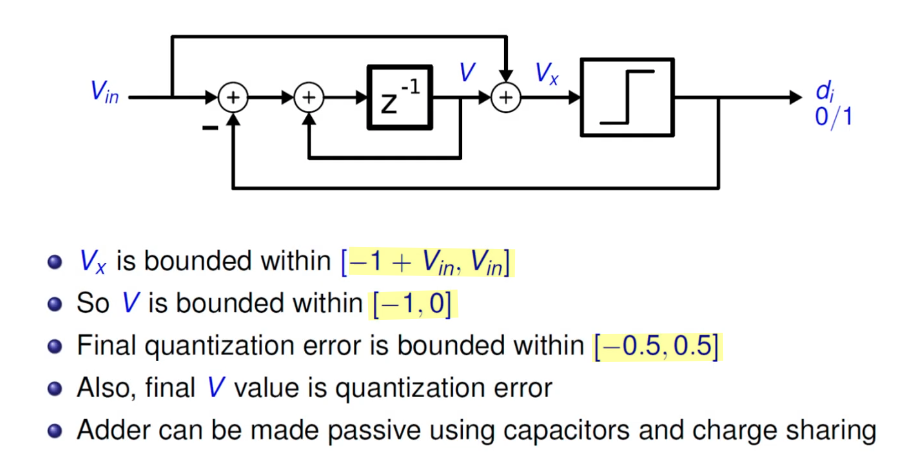
Incremental ADC

image-20250615124340044

image-20250615162024564

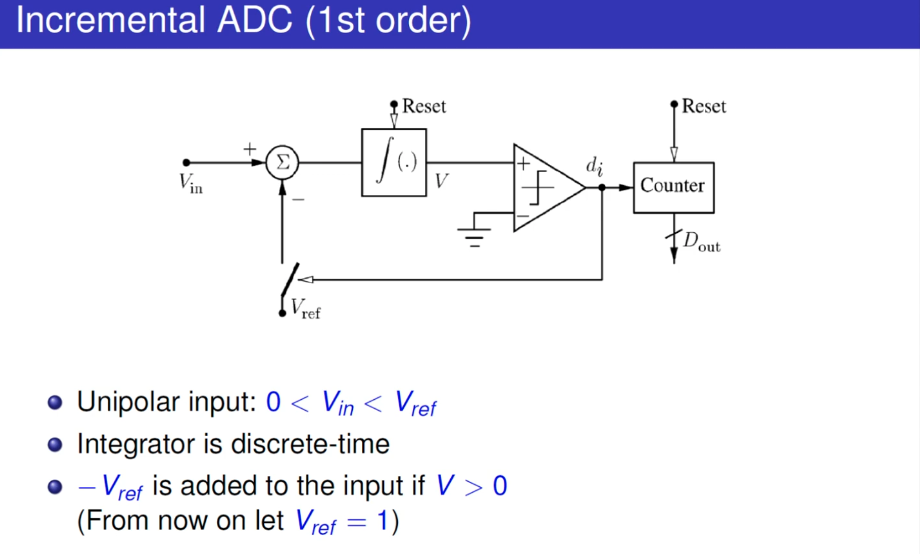
image-20250615162339449

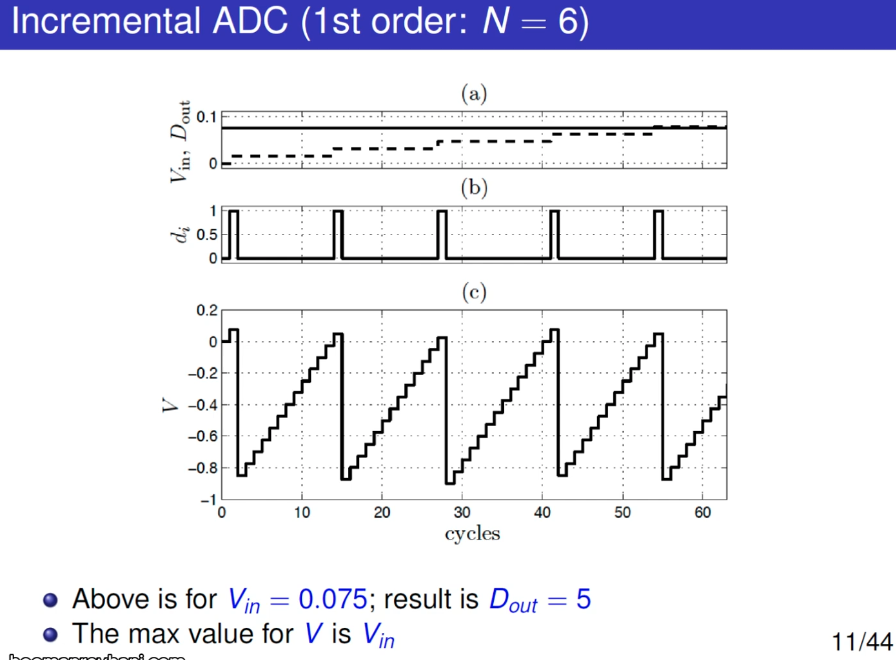
image-20250615162358247

image-20250615170209562

\[\begin{align} V &= 2^N V_\text{in} - D_\text{out}V_\text{ref} \\ D_\text{out} \frac{V_\text{ref}}{2^N} &= V_\text{in} - \frac{V}{2^N} \end{align}\]

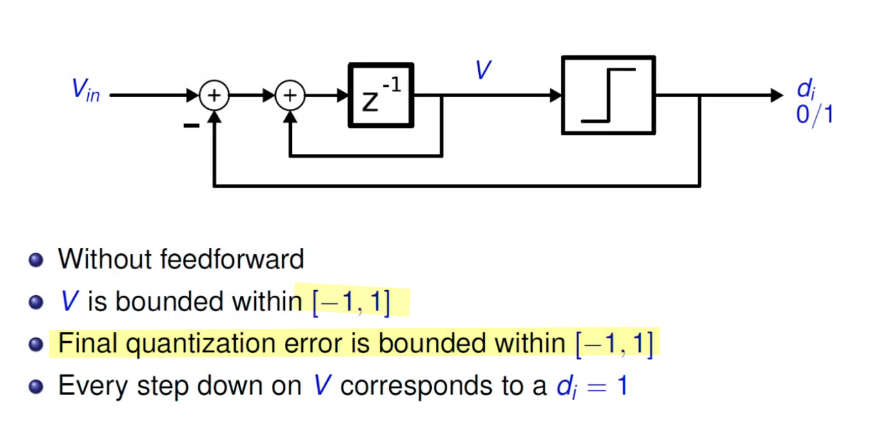
image-20250615164436626

image-20250615192031025

feedforward structure

??? TODO 📅

image-20250615165107485

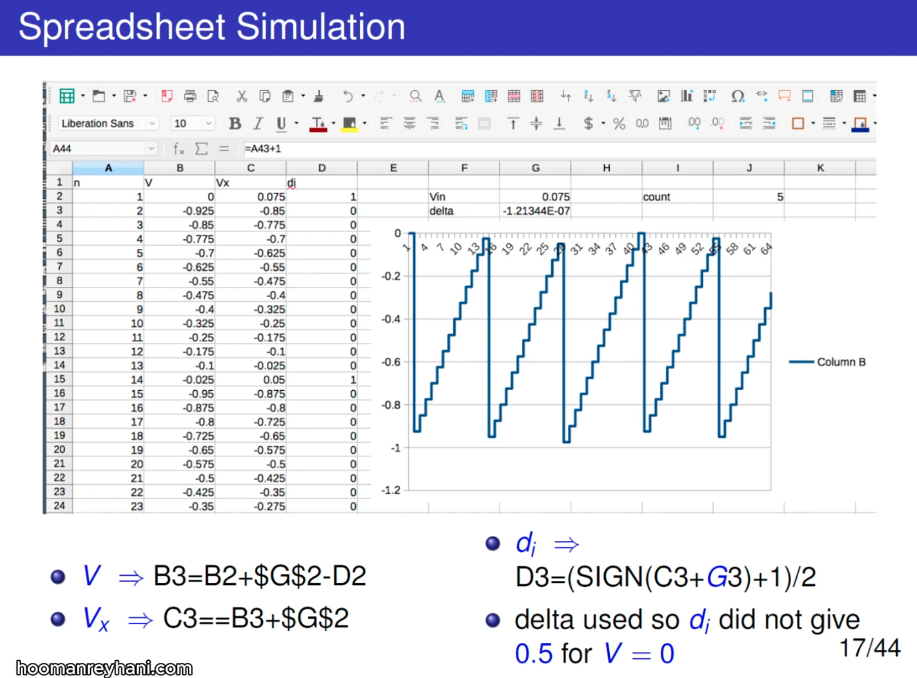
image-20250615175452958

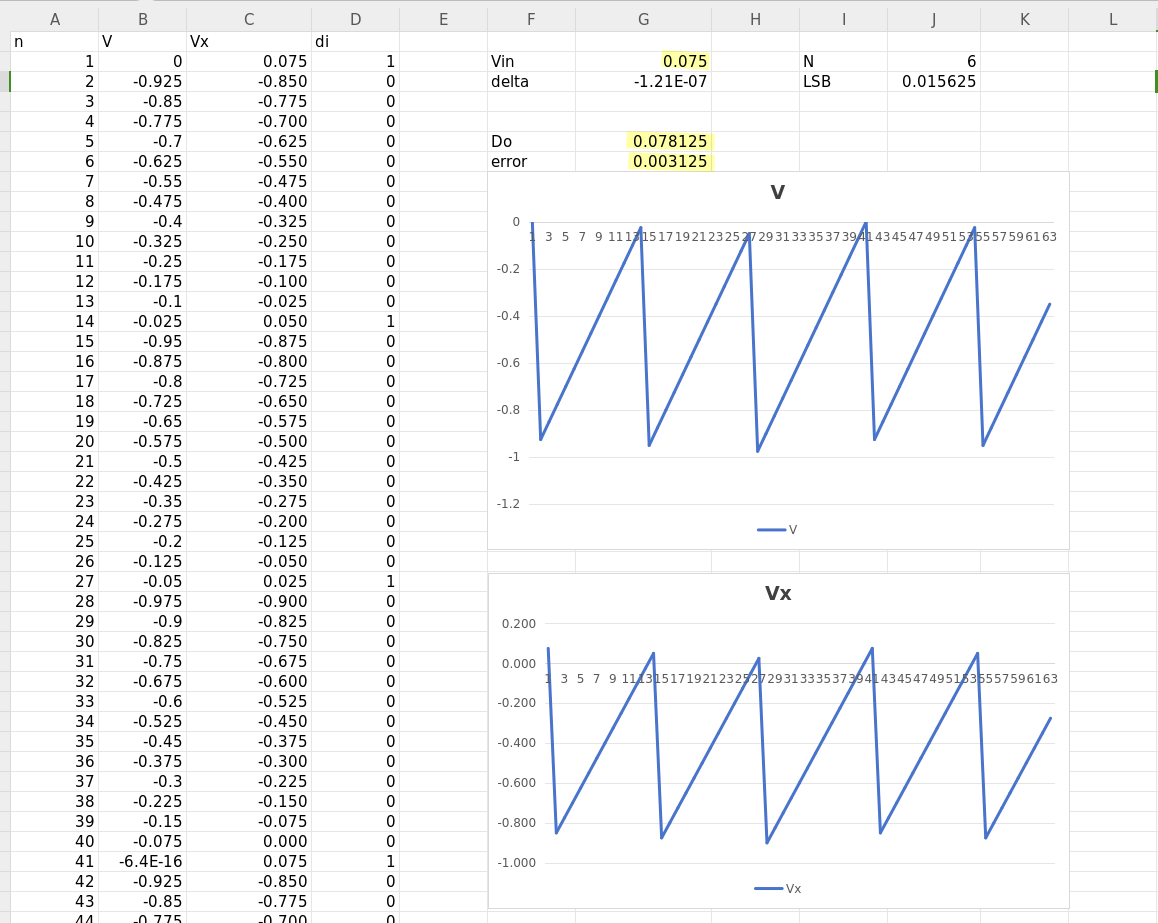
image-20250615194549768

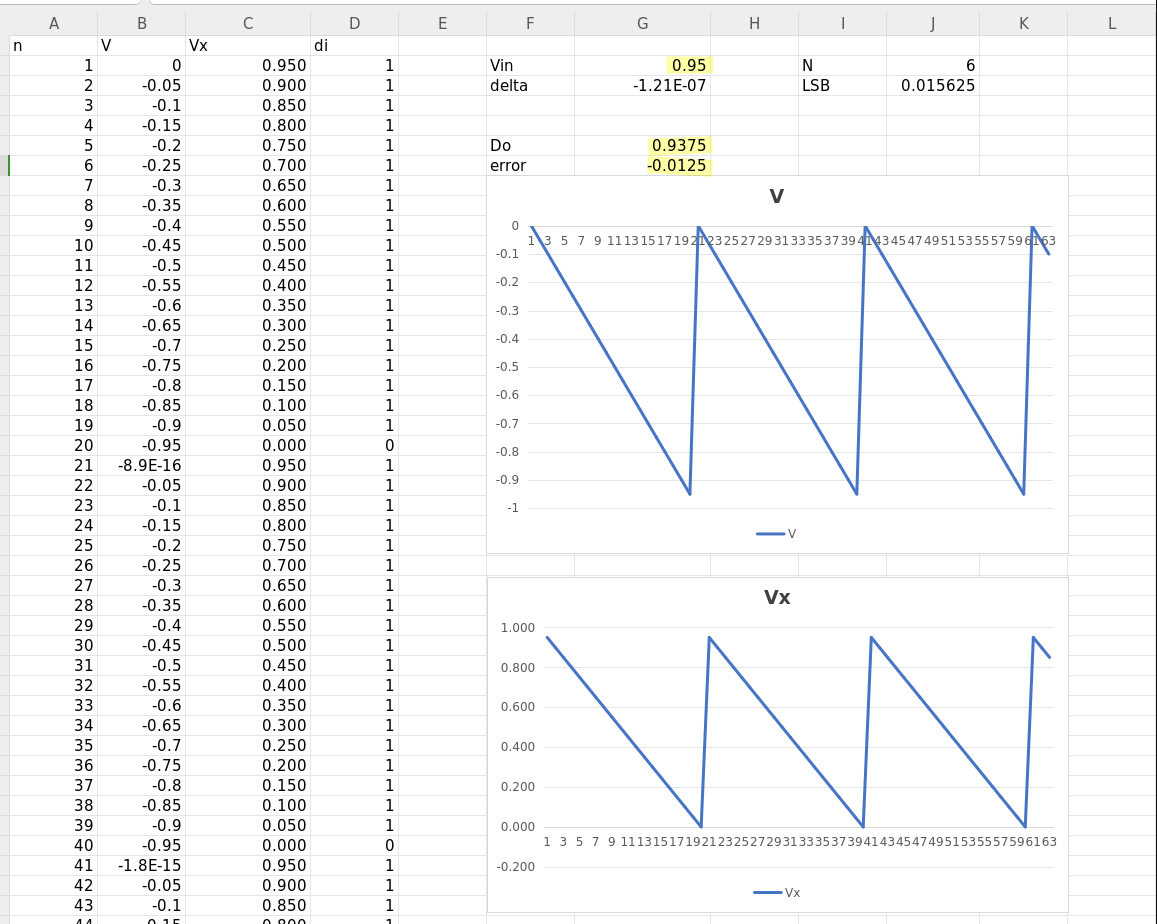
image-20250615194825368

image-20250615195150811

Discrete-Time Integrators

Delaying Integrator

Delay-free Integrator

image-20250615124417691

reference

David Johns (University of Toronto) "Oversampled Data Converters" Course (2019) [https://youtu.be/qIJ2LORYmyA?si=_pGb18rhsMUZ-lAf]