PI-based CDR

Phase Interpolator (PI)

!!! Clock Edges

And for a phase interpolator, you need those reference clocks to be completely the opposite. Ideally they would be triangular shaped

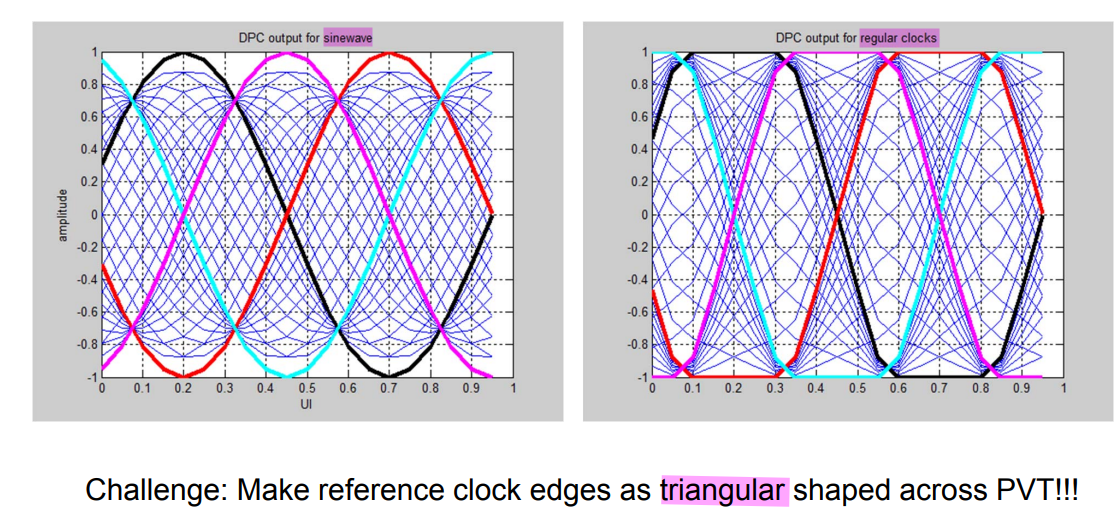
four input clocks given by the cyan, black, magenta, red

John T. Stonick, ISSCC 2011 tutorial. "DPLL Based Clock and Data Recovery" [https://www.nishanchettri.com/isscc-slides/2011%20ISSCC/TUTORIALS/ISSCC2011Visuals-T5.pdf]

kink problem

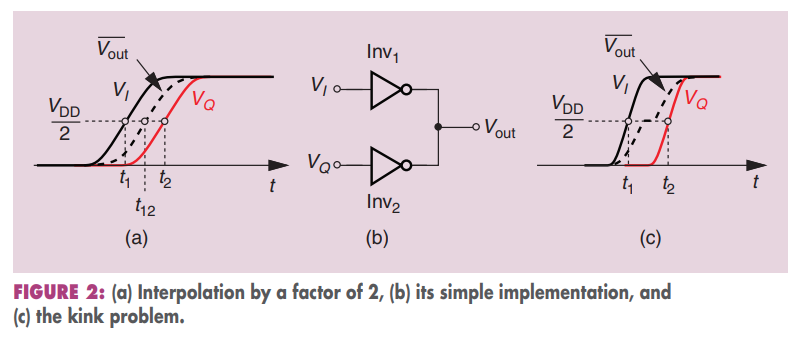
B. Razavi, "The Design of a Phase Interpolator [The Analog Mind]," IEEE Solid-State Circuits Magazine, Volume. 15, Issue. 4, pp. 6-10, Fall 2023.(https://www.seas.ucla.edu/brweb/papers/Journals/BR_SSCM_4_2023.pdf)

Predistortion - sinusoidal

the interpolating inverters near the midscale can be made weaker so as to obtain more uniform phase increments. Alternatively, those at the top and bottom of the array can be made stronger

Single-Quadrant PI

\[ V_o(t) = m \cdot \sin(\omega t + \frac{\pi}{2}) + p\cdot \sin(\omega t) = m\cdot \cos(\omega t) + p\cdot \sin(\omega t) = \sqrt{m^2+p^2} \sin(\omega t + \phi) \]

where \(\tan \phi = \frac{m}{p} = \frac{1-p}{p}\) and \(p = \frac{1}{1+\tan \phi}\)

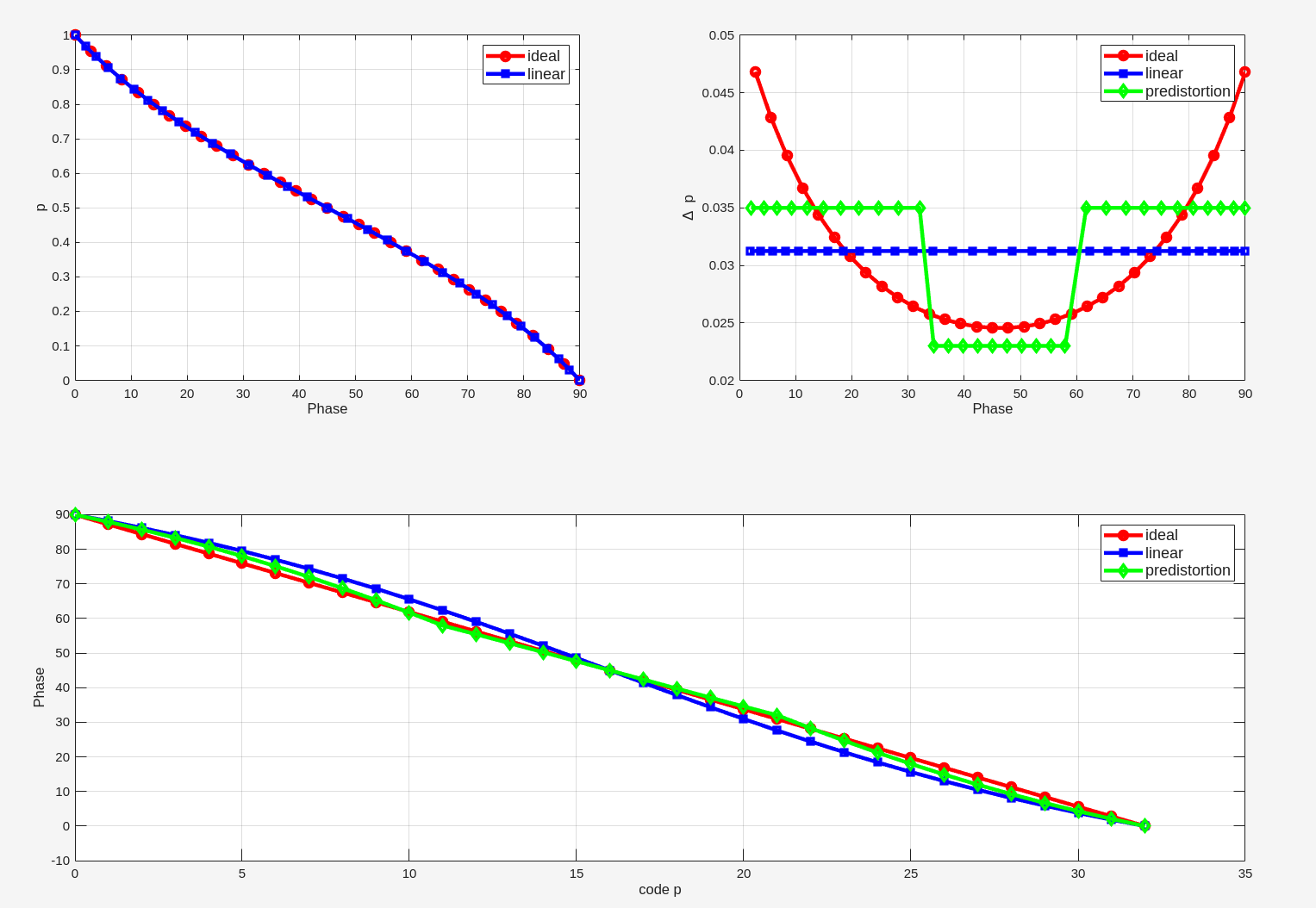
phi = (32:-1:0)./32*pi/2;
p_ideal = 1./(1+tan(phi));
delta_p_ideal = abs(p_ideal(1:end-1) - p_ideal(2:end));
phi_ideal = atan((1-p_ideal)./p_ideal);


p_lin = (0:1:32)/32;
phi_lin = atan((1-p_lin)./p_lin);
delta_p_lin = abs(p_lin(1:end-1) - p_lin(2:end));


delta_plr_predist = ones(1,11)*0.035;
delta_pm_predist = ones(1,10) * (1-2*sum(delta_plr_predist))/10;
delta_p_predist = [delta_plr_predist delta_pm_predist delta_plr_predist];
p_predist = [0 cumsum(delta_p_predist)];
phi_predist = atan((1-p_predist)./p_predist);


subplot(2,2,1)
plot(phi/pi*180, p_ideal, 'ro-', LineWidth=3)
hold on
plot(phi_lin/pi*180, p_lin, 'bs-', LineWidth=3)
grid on; legend('ideal', 'linear', fontsize=12)
xlabel('Phase'); ylabel('p')

subplot(2,2,2)
plot(phi(1:end-1)/pi*180, delta_p_ideal, 'ro-', LineWidth=3)
hold on
plot(phi_lin(1:end-1)/pi*180, delta_p_lin, 'bs-', LineWidth=3)
plot(phi_predist(1:end-1)/pi*180, delta_p_predist, 'gd-', LineWidth=3)
grid on; legend('ideal', 'linear', 'predistortion', fontsize=12)
xlabel('Phase'); ylabel('\Delta p')

subplot(2,2, [3,4])

plot(0:1:32, phi/pi*180, 'ro-', LineWidth=3)
hold on
plot(0:1:32, phi_lin/pi*180, 'bs-', LineWidth=3)
plot(0:1:32, phi_predist/pi*180, 'gd-', LineWidth=3)
grid on; legend('ideal', 'linear', 'predistortion', fontsize=12)
xlabel('code p'); ylabel('Phase')

Eight-Quadrant PI

\[\begin{align} V_o(t) &= m \cdot \sin(\omega t + \frac{\pi}{4}) + p\cdot \sin(\omega t) = \frac{\sqrt{2}}{2}m\cdot \cos(\omega t) + \left( \frac{\sqrt{2}}{2}m + p\right)\cdot \sin(\omega t) \\ &= \sqrt{m^2 + p^2 +\sqrt{2}pm}\cdot \sin(\omega t + \phi) \end{align}\]

where \(\tan\phi = \frac{\sqrt{2}m}{\sqrt{2}m+2p} = \frac{\sqrt{2}-\sqrt{2}p}{\sqrt{2}+(2-\sqrt{2})p}\)

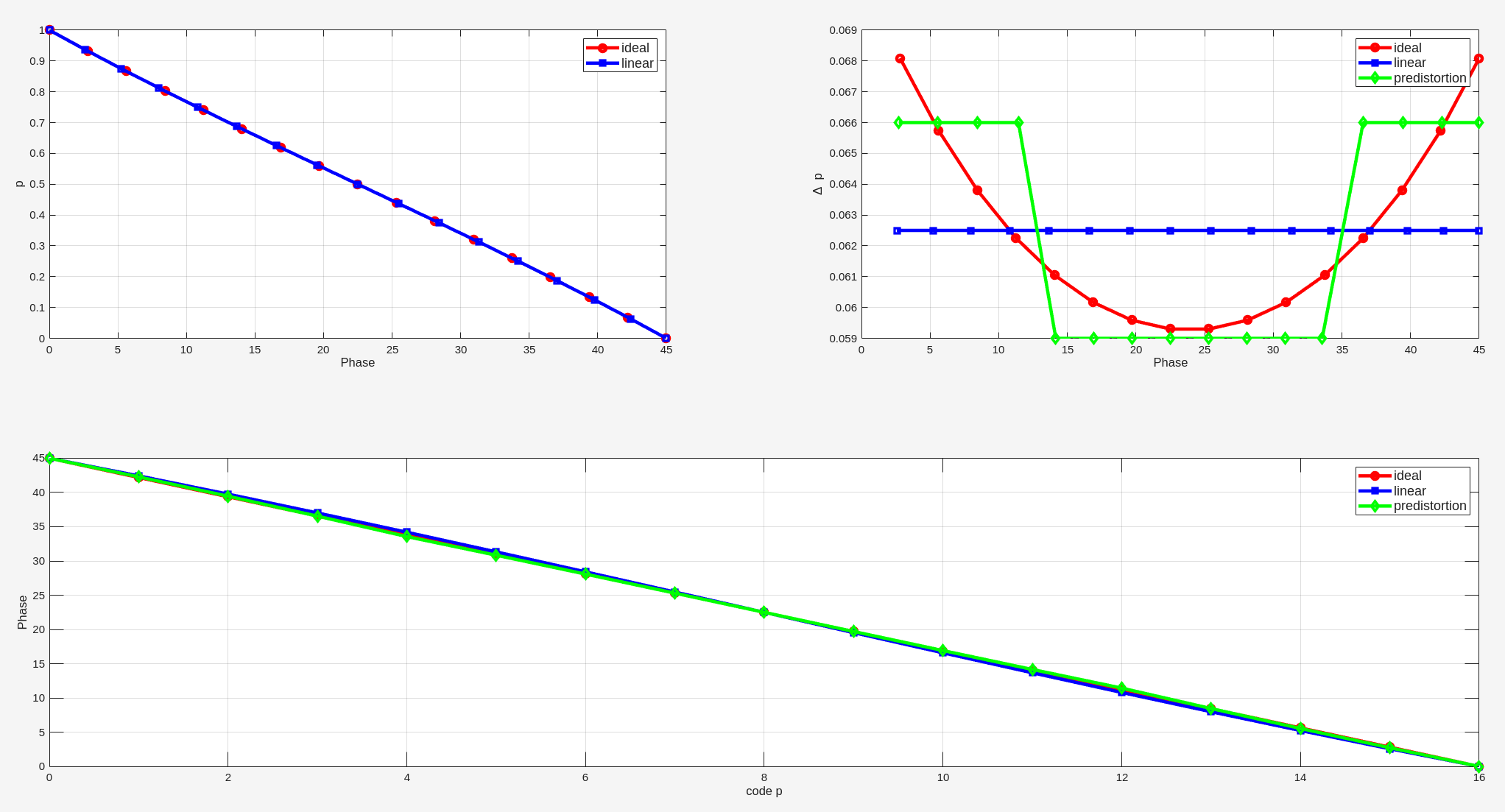
phi = (16:-1:0)./16*pi/4;
p_ideal = 2^0.5*(1-tan(phi))./(2*tan(phi)+2^0.5*(1-tan(phi)));
delta_p_ideal = abs(p_ideal(1:end-1) - p_ideal(2:end));
phi_ideal = atan((2^0.5 - 2^0.5*p_ideal)./(2^0.5 + (2-2^0.5)*p_ideal));


p_lin = (0:1:16)/16;
phi_lin = atan((2^0.5 - 2^0.5*p_lin)./(2^0.5 + (2-2^0.5)*p_lin));
delta_p_lin = abs(p_lin(1:end-1) - p_lin(2:end));


delta_plr_predist = ones(1,4)*0.066;
delta_pm_predist = ones(1,8) * (1-2*sum(delta_plr_predist))/8;
delta_p_predist = [delta_plr_predist delta_pm_predist delta_plr_predist];
p_predist = [0 cumsum(delta_p_predist)];
phi_predist = atan((2^0.5 - 2^0.5*p_predist)./(2^0.5 + (2-2^0.5)*p_predist));


subplot(2,2,1)
plot(phi/pi*180, p_ideal, 'ro-', LineWidth=3)
hold on
plot(phi_lin/pi*180, p_lin, 'bs-', LineWidth=3)
grid on; legend('ideal', 'linear', fontsize=12)
xlabel('Phase'); ylabel('p')

subplot(2,2,2)
plot(phi(1:end-1)/pi*180, delta_p_ideal, 'ro-', LineWidth=3)
hold on
plot(phi_lin(1:end-1)/pi*180, delta_p_lin, 'bs-', LineWidth=3)
plot(phi_predist(1:end-1)/pi*180, delta_p_predist, 'gd-', LineWidth=3)
grid on; legend('ideal', 'linear', 'predistortion', fontsize=12)
xlabel('Phase'); ylabel('\Delta p')

subplot(2,2, [3,4])

plot(0:1:16, phi/pi*180, 'ro-', LineWidth=3)
hold on
plot(0:1:16, phi_lin/pi*180, 'bs-', LineWidth=3)
plot(0:1:16, phi_predist/pi*180, 'gd-', LineWidth=3)
grid on; legend('ideal', 'linear', 'predistortion', fontsize=12)
xlabel('code p'); ylabel('Phase')

Predistortion - square wave

Weinlader, Daniel, Thomas H. Lee and James A. Gasbarro. "Precision CMOS receivers for VLSI testing applications." (2001). [https://www-vlsi.stanford.edu/people/alum/pdf/0111_Weinlader_Precision_CMOS_Receivers_.pdf]

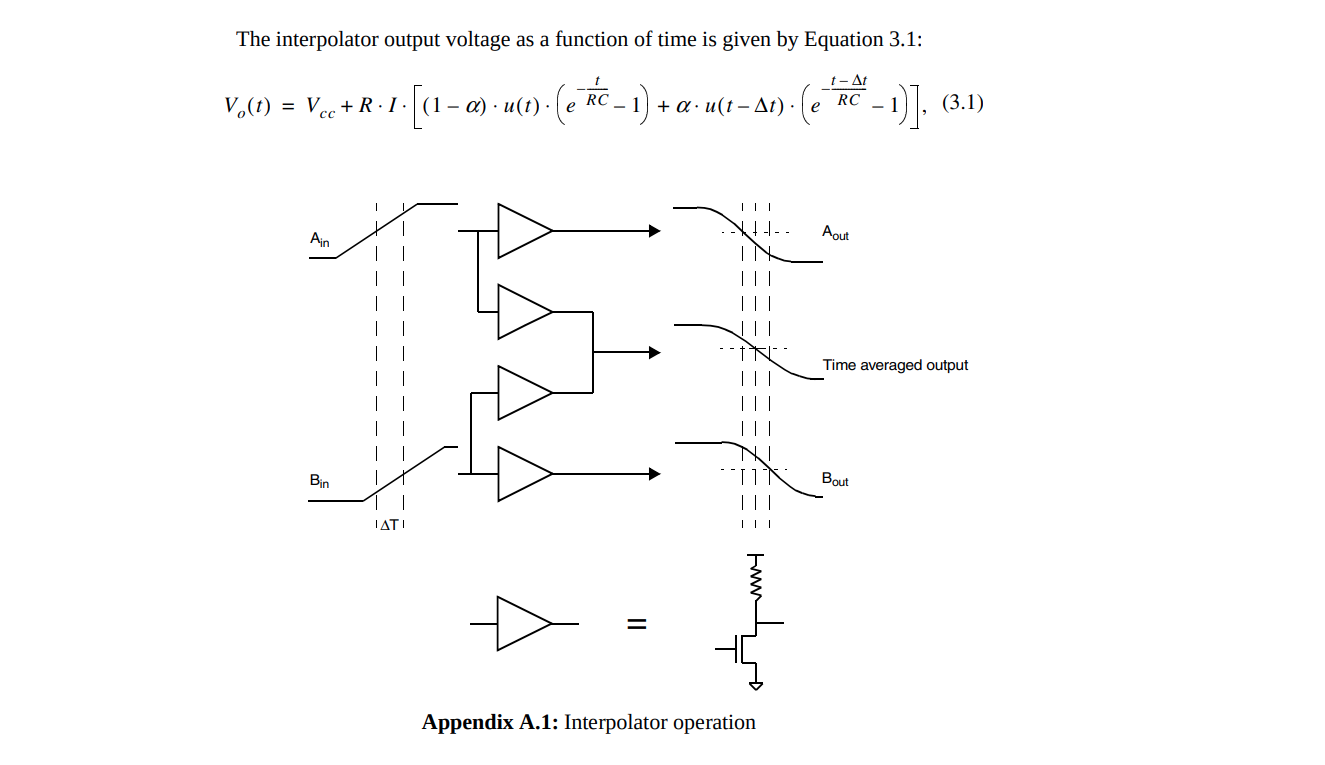
Suppose \(V_i(t) = 1- e^{-\frac{t}{\tau}}\) and \(V_q(t) = 1-e^{-\frac{t-\Delta t}{\tau}}\) with \(t\ge \Delta t\) \[ \frac{1}{2} = (1-\alpha)\cdot V_i(t) + \alpha \cdot V_q(t) \] yield triggering time \[ t = \tau \ln\left[ 1 + \alpha \left(e^{\frac{\Delta t}{\tau}}-1\right)\right] + \tau \ln 2 \] Then \[\begin{align} \frac{\partial t}{\partial \alpha} &= \tau \frac{e^{\frac{\Delta t}{\tau }}-1}{1+\alpha(e^{\frac{\Delta t}{t}}-1)} \gt 0 \\ \frac{\partial^2 t}{\partial \alpha^2} &= -\tau \frac{\left(e^{\frac{\Delta t}{\tau }}-1\right)^2}{\left(1+\alpha(e^{\frac{\Delta t}{t}}-1)\right)^2} \lt 0 \end{align}\]

As a conclusion, heavier weight while \(\alpha\) approaching to 1 in order to improve linearity

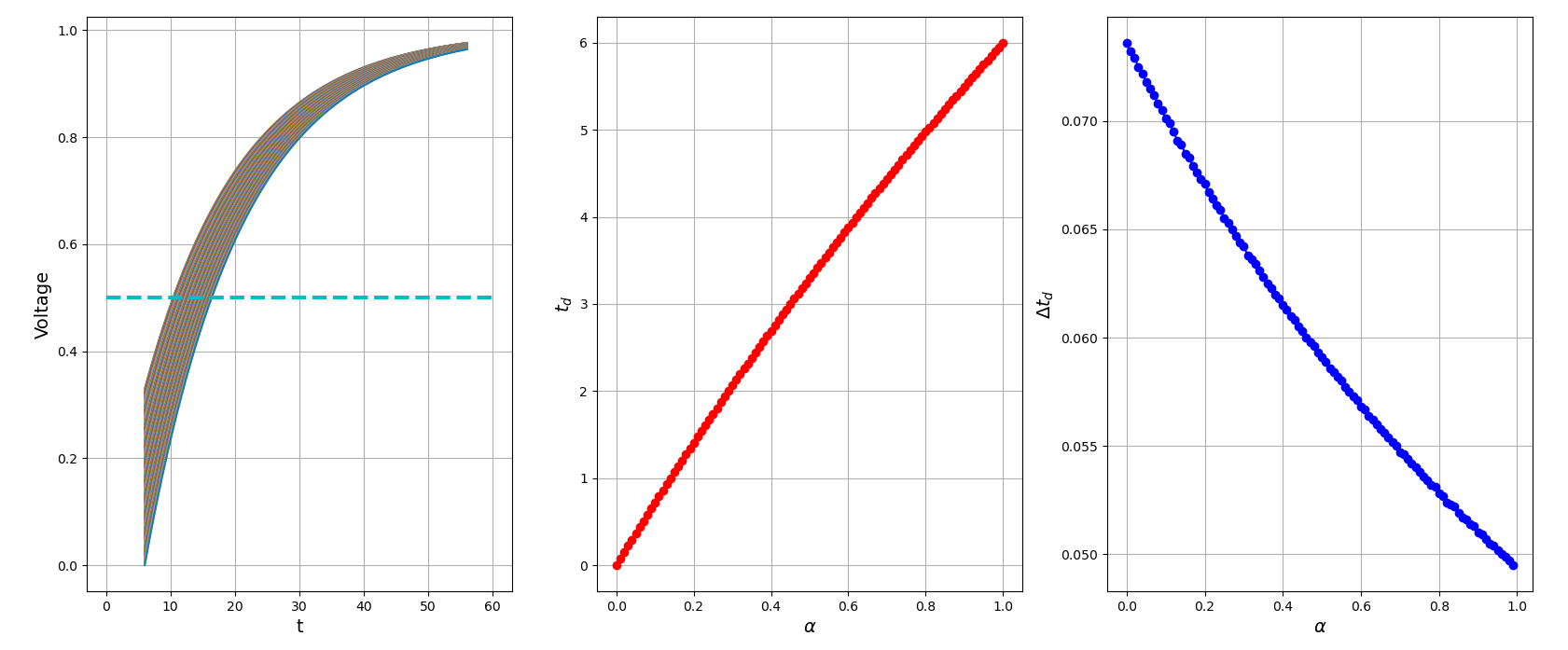
import numpy as np
import matplotlib.pyplot as plt

tau = 15  # ps
t = np.linspace(6, 56, 500001)

vi = 1- np.exp(-t/tau)
vq = 1 - np.exp(-(t-6)/tau)	# \Detla t = 6

td = []
alpha_list = np.linspace(0, 101, 101,  endpoint=False)/100

plt.figure(figsize=(20,8))
plt.subplot(1, 3, 1)
for alpha in alpha_list:
    viq = (1-alpha) * vi + alpha*vq
    differences  = np.abs((viq - 0.5))
    closest_index = np.argmin(differences)
    t_closest = t[closest_index]
    td.append(t_closest)
    plt.plot(t,viq)
plt.plot([0, 60], [0.5,0.5], '--c', linewidth=3); plt.grid()
plt.xlabel('t', fontsize=14); plt.ylabel('Voltage', fontsize=14)

td = np.array(td) - td[0]
d_td = td[1:] - td[:-1]

plt.subplot(1, 3, 2)
plt.plot(alpha_list, td, 'ro-', linewidth=2)
plt.grid(); plt.xlabel(r'$\alpha$', fontsize=14); plt.ylabel(r'$t_d$', fontsize=14)

plt.subplot(1, 3, 3)
plt.plot(alpha_list[:-1], d_td, 'bo-')
plt.grid(); plt.xlabel(r'$\alpha$', fontsize=14); plt.ylabel(r'$\Delta t_d$', fontsize=14)

plt.show()

Input/Output amplitude

A constant Output amplitude is desired because the swing-dependent delay characteristic of the CML-to-CMOS (C2C) circuit results in AM–PM distortion which eventually manifests as phase nonlinearity

Current-Mode Phase Interpolator

Voltage-Mode Phase Interpolator

Integrating-Mode Phase Interpolator

PI vs. PLL based CDR

PCI Express Jitter Modeling Revision 1.0RD July 14, 2004

reference

A. K. Mishra, Y. Li, P. Agarwal and S. Shekhar, "Improving Linearity in CMOS Phase Interpolators," in IEEE Journal of Solid-State Circuits, vol. 58, no. 6, pp. 1623-1635, June 2023 [pdf]

Cortiula A, Menin D, Bandiziol A, Driussi F, Palestri P. Modeling of Phase-Interpolator-Based Clock and Data Recovery for High-Speed PAM-4 Serial Interfaces. Electronics. 2025; [https://www.mdpi.com/2079-9292/14/10/1979]

G. Souliotis, A. Tsimpos and S. Vlassis, "Phase Interpolator-Based Clock and Data Recovery With Jitter Optimization," in IEEE Open Journal of Circuits and Systems, vol. 4, pp. 203-217, 2023 [https://ieeexplore.ieee.org/document/10184121]

B. Razavi, "The Design of a Phase Interpolator [The Analog Mind]," in IEEE Solid-State Circuits Magazine, vol. 15, no. 4, pp. 6-10, Fall 2023 [https://www.seas.ucla.edu/brweb/papers/Journals/BR_SSCM_4_2023.pdf]