Precision Techniques

Posted on Edited on In

Correlated Double Sampling (CDS)

TODO 📅

Dynamic Element Matching (DEM)

TODO 📅

image-20241112214430191

Galton, Ian. (2010). Why dynamic-element-matching DACs work. Circuits and Systems II: Express Briefs, IEEE Transactions on. 57. 69 - 74. 10.1109/TCSII.2010.2042131. [https://sci-hub.se/10.1109/TCSII.2010.2042131]

KHIEM NGUYEN. Analog Devices Inc, "Practical Dynamic Element Matching Techniques for 3-level Unit Elements" [https://picture.iczhiku.com/resource/eetop/shihEDaaoJjFdCVc.pdf]

E. Alvarez-Fontecilla, P. S. Wilkins and S. C. Rose, "Understanding High-Resolution Dynamic Element Matching DACs [Feature]," in IEEE Circuits and Systems Magazine, vol. 23, no. 4, pp. 34-43, Fourthquarter 2023

E. Alvarez-Fontecilla and P. S. Wilkins, "Linearity Through Democracy [Feature]," in IEEE Circuits and Systems Magazine, vol. 25, no. 1, pp. 58-69, Firstquarter 2025

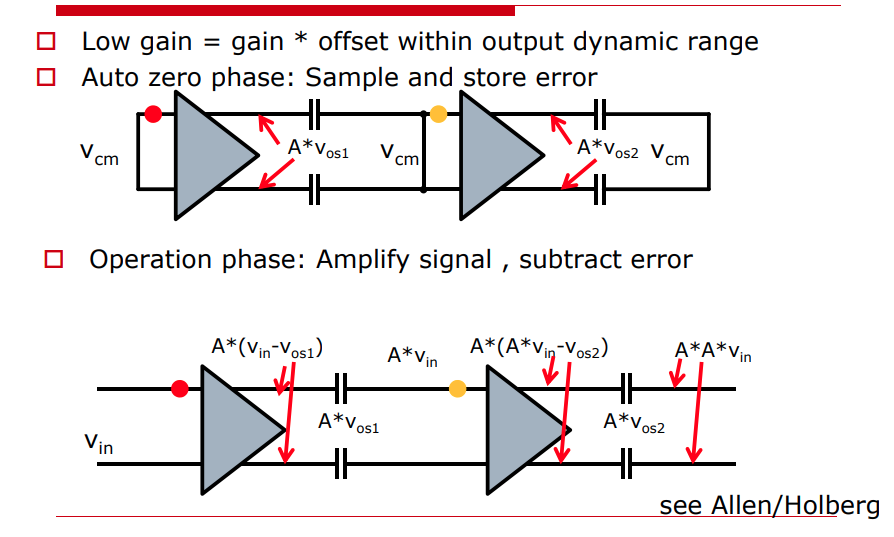
Autozeroing

offset is sampled and then subtracted from the input

Measure the offset somehow and then subtract it from the input signal

low gain comparator

image-20241023224809158

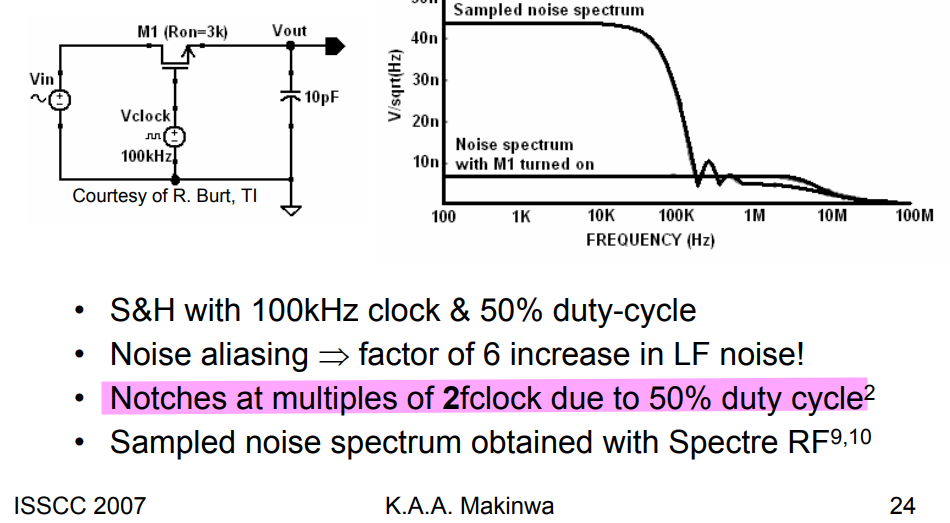
Residual Noise of Auto-zeroing

image-20240826212343905

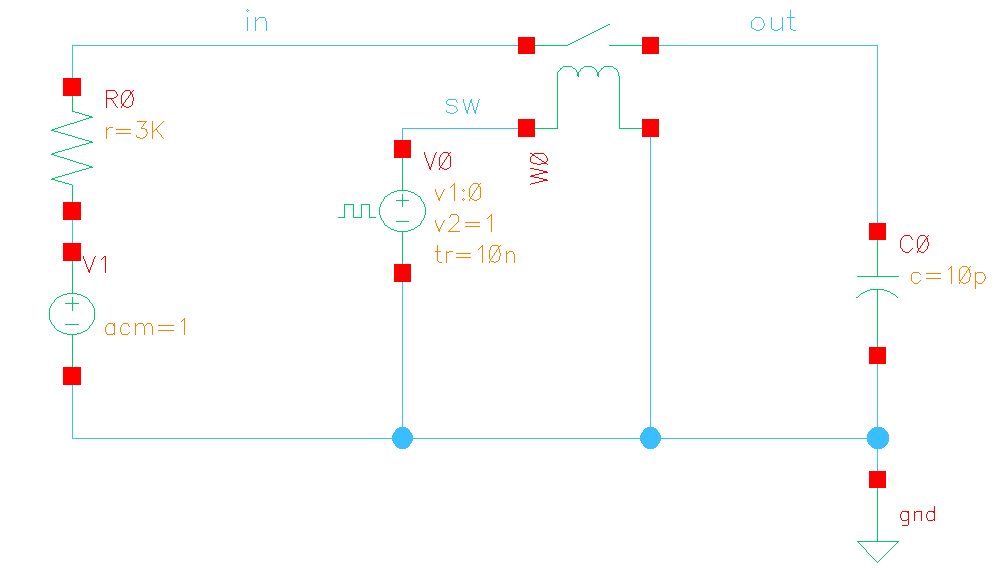
image-20240826213958740

pnosie Noise Type: timeaverage

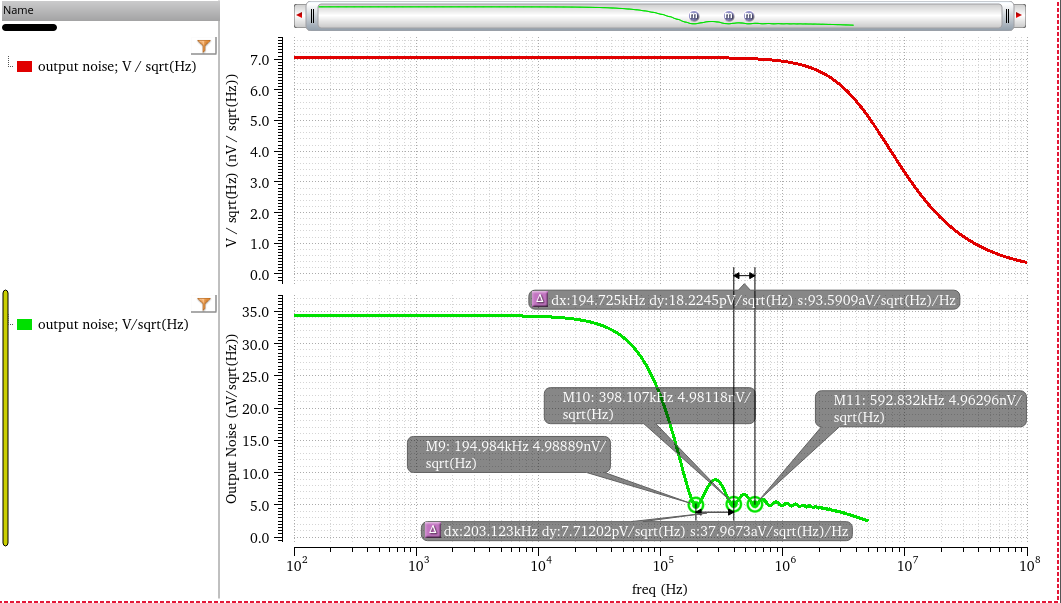
image-20240826214306376

\(\Pi\)-Capacitor

pi_Cap.drawio

\[\begin{align} (V_a-V_{a0})C_0 + (\overline{V_a - V_b} - \overline{V_{a0} - V_{b0}})C_1 &= \Delta Q_a \\ (V_b-V_{b0})C_0 + (\overline{V_b - V_a} - \overline{V_{b0} - V_{a0}})C_1 &= \Delta Q_b \end{align}\]

therefore we obtain \[\begin{align} V_a + V_b &= \frac{\Delta Q_a + \Delta Q_b}{C_0} + V_{a0} + V_{b0} \\ V_a - V_b &= \frac{\Delta Q_a - \Delta Q_b}{C_0+2C_1} + V_{a0} - V_{b0} \end{align}\] Then \[\begin{align} V_a &= \frac{\Delta Q_a(C_0+C_1)+\Delta Q_b C_1}{C_0(C_0+2C_1)} + V_{a0} \\ V_b &= \frac{\Delta Q_aC_1+\Delta Q_b (C_0+C_1)}{C_0(C_0+2C_1)} + V_{b0} \end{align}\]

rearrange the above equation \[\begin{align} V_a &= \frac{\Delta Q_a}{C_0} + \frac{\Delta Q_b-\Delta Q_a}{C_0(\frac{C_0}{C_1}+2)} + V_{a0} \\ V_b &= \frac{\Delta Q_b}{C_0} + \frac{\Delta Q_a-\Delta Q_b}{C_0(\frac{C_0}{C_1}+2)} + V_{b0} \end{align}\]

The difference between \(V_a\) and \(V_b\) \[ V_a - V_b = \frac{I_a-I_b}{C_0+2C_1}t + V_{a0} - V_{b0} \]

\(C_1\) save total capacitor area while retaining the same \(V_a - V_b\) due to \(\Delta I_{a,b}\), in comparison to \(C_0\)

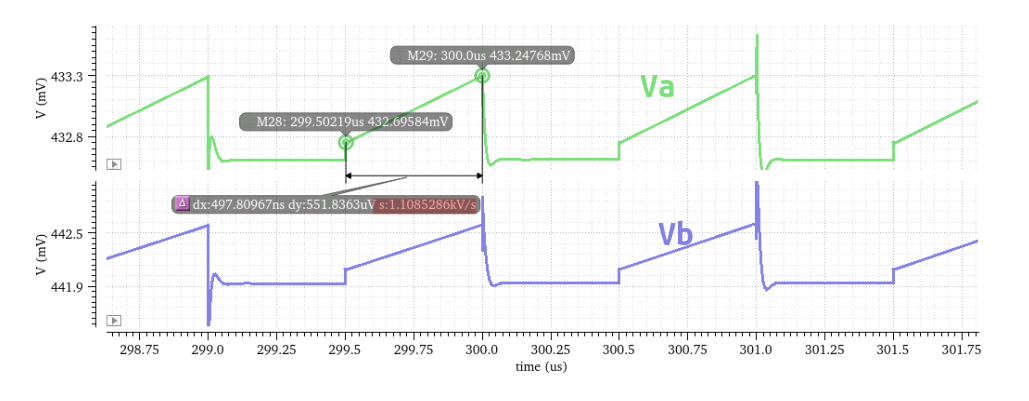
image-20250802170659120

at autozero phase \[\begin{align} I_{a0} &= \frac{1}{2}\mu C_{OX}\frac{W}{L}(V_{a0} - V_{TH})^2 \\ I_{Rb} &= \frac{1}{2}\mu C_{OX}\frac{W}{L}(V_{b0} - V_{TH})^2 \end{align}\]

then \[ \Delta I_0 = \frac{1}{2}(V_{a0} - V_{b0})(g_{m,a0}+g_{m,b0}) \] where \(g_{m,a0}+g_{m,b0} = \mu C_{OX}\frac{W}{L}(V_{a0}+V_{b0} - 2V_{TH})\)

at comparison phase \[\begin{align} I_{a1} &= \frac{1}{2}\mu C_{OX}\frac{W}{L}(V_{a1} - V_{TH})^2 \\ I_{b1} &= \frac{1}{2}\mu C_{OX}\frac{W}{L}(V_{b1} - V_{TH})^2 \end{align}\]

then \[ \Delta I_1 = \frac{1}{2}(V_{a1} - V_{b1})(g_{m,a1}+g_{m,b1}) \] That is, \(g_{m,a1}+g_{m,b1} = \mu C_{OX}\frac{W}{L}(V_{a1}+V_{b1} - 2V_{TH})\)

To minimize the difference between \(\Delta I_1\) and \(\Delta I_0\), the drift of both differential and common mode between \(V_a\) and \(V_b\) shall be alleviated

Chopping

offset is modulated away from the signal band and then filtered out

Modulate the offset away from DC and then filter it out

Good: Magically reduces offset, 1/f noise, drift

Bad: But creates switching spikes, chopper ripple and other artifacts …

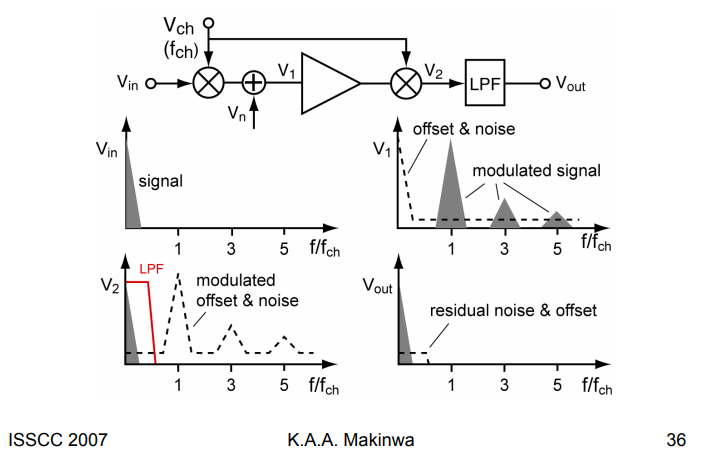
Chopping in the Frequency Domain

Square-wave Modulation

definition of convolution \(y(t) = x(t)*h(t)= \int_{-\infty}^{\infty} x(\tau)h(t-\tau)d\tau\)

for real signal \(H(j\omega)^*=H(-j\omega)\)​

image-20240903222441433

\[ H(j\hat{\omega})*H(j\hat{\omega}) = \int_{-\infty}^{\infty}H(j\omega)H(j(\hat{\omega}-\omega))d\omega \]

sq_mod.drawio

The Fourier Series of squarewave \(x(t)\) with amplitudes \(\pm 1\), period \(T_0\)

\[ C_n = \left\{ \begin{array}{cl} 0 &\space \ n=0 \\ 0 &\space \ n=\text{even} \\ |\frac{2}{n\pi}| &\space n=\pm 1,\pm 5,\pm9, ... \\ -|\frac{2}{n\pi}| &\space n=\pm 3,\pm 7,\pm11, ... \end{array} \right. \]

The Fourier transform of \(s(t)=x(t)x(t)\), and we know \[\begin{align} S(j2n\omega_0) &= \frac{1}{2\pi}\int X(j(2n\omega_0 -\omega))X(j\omega) d\omega\\ &= \frac{1}{2\pi}\int X(j(\omega-2n\omega_0))X(j\omega) d\omega \end{align}\]

Therefore \(n=0\) \[ S(j0) = \frac{1}{2\pi} (2\pi)^2\cdot \frac{4}{\pi ^2}2\sum_{n=0}^{+\infty}\frac{1}{(2n+1)^2} \delta(\omega) = 2\pi \delta(\omega) \]

if \(n=1\)

\[\begin{align} S(j2\omega_0) &= \frac{1}{2\pi} (2\pi)^2\cdot \frac{4}{\pi ^2}\left(1 - 2\sum_{n=0}^{+\infty}\frac{1}{(2n+1)(2n+3)} \right) \\ &= \frac{1}{2\pi} (2\pi)^2\cdot \frac{4}{\pi ^2}\left(1 - 2\sum_{n=0}^{+\infty}\frac{1}{2}\left[\frac{1}{2n+1}- \frac{1}{2n+3}\right] \right) \\ &= 0 \end{align}\]

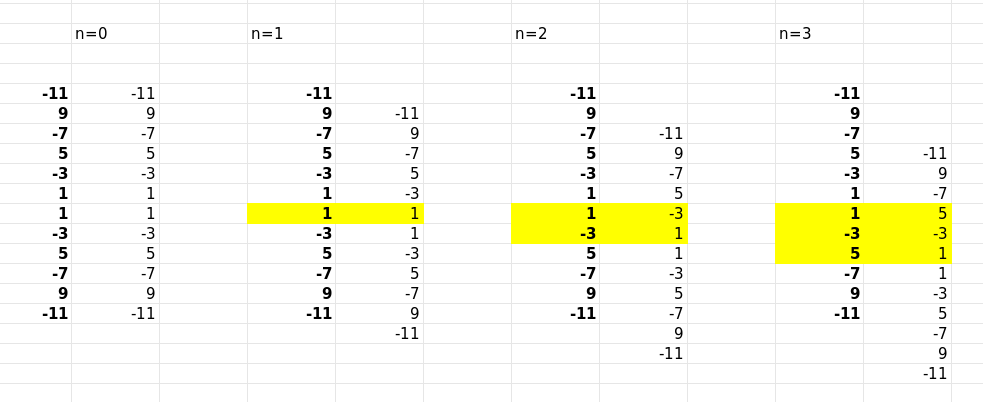
image-20241013125713945

\(n=2\) \[\begin{align} \sum &= -\frac{2}{3} + 2\left(\frac{1}{1\times 5}+ \frac{1}{3\times 7}+ \frac{1}{5\times 9} + \frac{1}{7\times 11}+...\right) \\ &= -\frac{2}{3} + 2\cdot \frac{1}{4}\left(\frac{1}{1}-\frac{1}{5}+ \frac{1}{3}- \frac{1}{7}+ \frac{1}{5} - \frac{1}{9} +\frac{1}{7}-\frac{1}{11}+...\right) \\ &= -\frac{2}{3} + 2\cdot \frac{1}{4}\frac{4}{3} = 0 \end{align}\]

That is, the input signal remains the same after chopping or squarewave up/down modulation

EXAMPLE 2.7 in R. E. Ziemer and W. H. Tranter, Principles of Communications, 7th ed., Wiley, 2013 [pdf]

Prove that \(\pi^2/8 = 1 + 1/3^2 + 1/5^2 + 1/7^2 + \cdots\) [https://math.stackexchange.com/a/2348996]

Bandwidth & Gain Accuracy

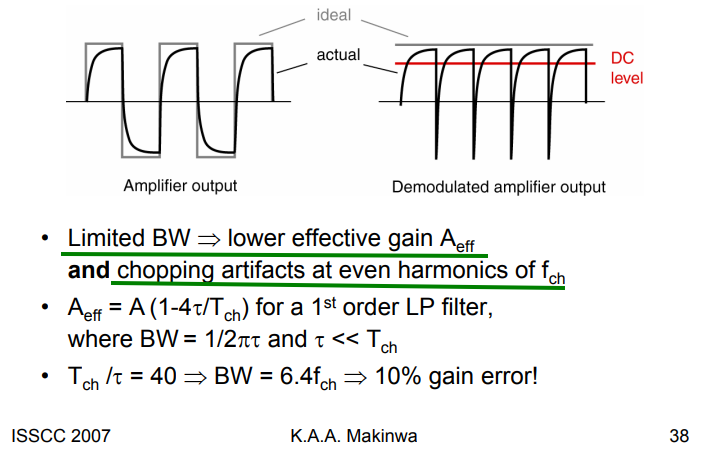
image-20240903225224732

  • lower effective gain: DC level at the output of the amplifiers is a bit less than what it should be

  • chopping artifacts at the even harmonics: frequency of output is \(2f_{ch}\)

Below we justify \(A_\text{eff} = A(1-4\tau/T_\text{ch})\) \[\begin{align} V_o(t) &= A + (V_0-A)e^{-t/\tau} \\ V_o(T/2) &= -V_0 \end{align}\]

then \[ V_0 = -A\frac{1-e^{-T/2\tau}}{1+e^{-T/2\tau}} \] Then DC level is \[ A_\text{eff} = \frac{1}{T/2}\int_0^{T/2} V_o(t)dt = A\left(1-\frac{4\tau}{T}\cdot \frac{1-e^{-T/2\tau}}{1+e^{-T/2\tau}}\right)\approx A\left(1-\frac{4\tau}{T}\right) \]

where assuming \(\tau \ll T\)

REF. [https://raytroop.github.io/2023/01/01/insight/#rc-charge-and-discharge]

chopping_OTA_limitedBW.drawio

Residual Offset of Chopping

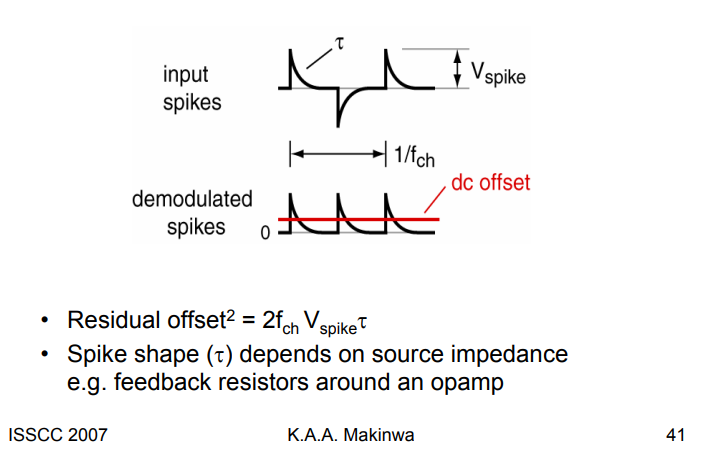
image-20240903222425730

assume input spikes can be expressed as \[ V_\text{spike}(t) = V_o e^{-\frac{t}{\tau}} \]

Then, residual offset is

\[\begin{align} \overline{V_\text{os}} &= \frac{2\int_0^{T_{ch}/2}V_\text{spike}(t)dt}{T_{ch}} \\ &= 2f_{ch}V_o\int_0^{T_{ch}/2} e^{-\frac{t}{\tau}}dt\\ &= 2f_{ch}V_o\tau\int_0^{T_{ch}/2\tau} e^{-\frac{t}{\tau}}d\frac{t}{\tau} \\ &\approx 2f_{ch}V_o\tau \end{align}\]​

Ripple Cancellation after Chopping

On-chip analog filter is not good enough due to limited cutoff frequency

rippleCancel.drawio

at \(\Phi_+\) phase \[ \left\{ \begin{array}{cl} \Delta V_\text{os}[n] &= \frac{I_l[n]-I_r[n-1]}{G_m} \\ \left(I_0+\frac{V_\text{os0}-\Delta V_\text{os}[n]}{R_E}\right)\beta &= I_l[n]+I_r[n-1] \end{array} \right. \] Then \[ \left\{ \begin{array}{cl} I_r[n-1] &= \frac{-G_mR_E-\beta}{2R_E}\cdot \Delta V_\text{os}[n] + \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \\ I_l[n] &= \frac{G_mR_E-\beta}{2R_E}\cdot \Delta V_\text{os}[n] + \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \end{array} \right. \] at \(\Phi_-\) phase \[ \left\{ \begin{array}{cl} \Delta V_\text{os}[n] &= \frac{I_l[n-1]-I_r[n]}{G_m} \\ \left(I_0+\frac{-V_\text{os0}+\Delta V_\text{os}[n]}{R_E}\right)\beta &= I_l[n-1]+I_r[n] \end{array} \right. \] Then \[ \left\{ \begin{array}{cl} I_r[n] &= \frac{-G_mR_E+\beta}{2R_E}\cdot \Delta V_\text{os}[n] - \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \\ I_l[n-1] &= \frac{G_mR_E+\beta}{2R_E}\cdot \Delta V_\text{os}[n] - \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \end{array} \right. \] \(\Phi_+ \to \Phi_-\) state transformation \[ \left\{ \begin{array}{cl} I_r[n-1] &= \frac{-G_mR_E-\beta}{2R_E}\cdot \Delta V_\text{os}[n] + \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \\ I_l[n] &= \frac{G_mR_E-\beta}{2R_E}\cdot \Delta V_\text{os}[n] + \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \end{array} \right. \to \left\{ \begin{array}{cl} I_r[n+1] &= \frac{-G_mR_E+\beta}{2R_E}\cdot \Delta V_\text{os}[n+1] - \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \\ I_l[n] &= \frac{G_mR_E+\beta}{2R_E}\cdot \Delta V_\text{os}[n+1] - \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \end{array} \right. \] Two \(I_l[n]\) shall be equal, that is \[ \frac{G_mR_E-\beta}{2R_E}\cdot \Delta V_\text{os}[n] + \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 = \frac{G_mR_E+\beta}{2R_E}\cdot \Delta V_\text{os}[n+1] - \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \] Rearrange the above equation \[ \Delta V_\text{os}[n+1] = \frac{G_mR_E-\beta}{G_mR_E+\beta}\Delta V_\text{os}[n] + \frac{2\beta}{G_mR_E+\beta}V_\text{os0} \] \(\Phi_- \to \Phi_+\) state transformation \[ \left\{ \begin{array}{cl} I_r[n] &= \frac{-G_mR_E+\beta}{2R_E}\cdot \Delta V_\text{os}[n] - \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \\ I_l[n-1] &= \frac{G_mR_E+\beta}{2R_E}\cdot \Delta V_\text{os}[n] - \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \end{array} \right. \to \left\{ \begin{array}{cl} I_r[n] &= \frac{-G_mR_E-\beta}{2R_E}\cdot \Delta V_\text{os}[n+1] + \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \\ I_l[n+1] &= \frac{G_mR_E-\beta}{2R_E}\cdot \Delta V_\text{os}[n+1] + \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \end{array} \right. \] Two \(I_r[n]\) shall be equal, that is \[ \frac{-G_mR_E+\beta}{2R_E}\cdot \Delta V_\text{os}[n] - \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 = \frac{-G_mR_E-\beta}{2R_E}\cdot \Delta V_\text{os}[n+1] + \frac{\beta}{2R_E}V_\text{os0}+\frac{\beta}{2}I_0 \] Rearrange the above equation \[ \Delta V_\text{os}[n+1] = \frac{G_mR_E-\beta}{G_mR_E+\beta}\Delta V_\text{os}[n] + \frac{2\beta}{G_mR_E+\beta}V_\text{os0} \]

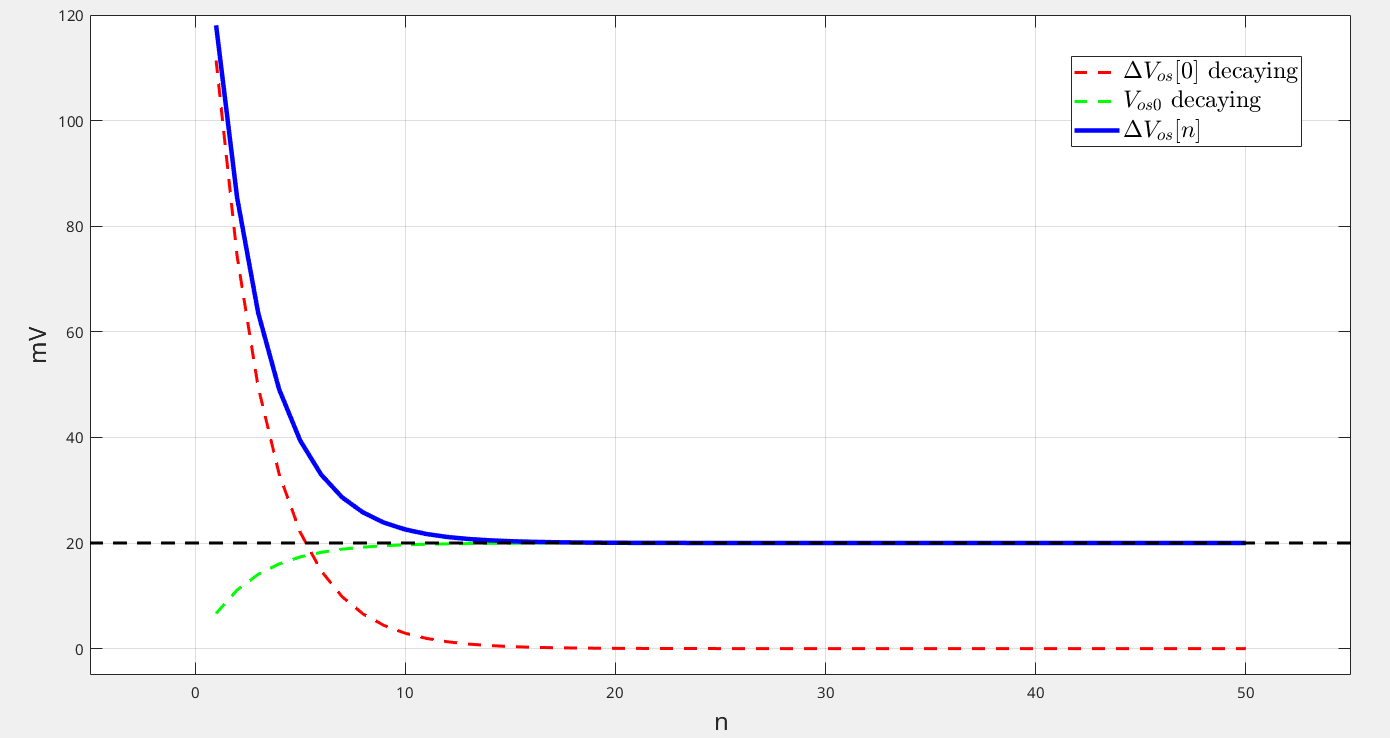
Both State-transition equations are same \[ \Delta V_\text{os}[n+1] = \frac{G_mR_E-\beta}{G_mR_E+\beta}\Delta V_\text{os}[n] + \frac{2\beta}{G_mR_E+\beta}V_\text{os0} \] With geometric progression sum formula \[ \Delta V_\text{os}[n] = \left(\frac{G_mR_E-\beta}{G_mR_E+\beta}\right)^n\cdot \Delta V_\text{os}[0] + \left[1-\left(\frac{G_mR_E-\beta}{G_mR_E+\beta}\right)^n\right]\cdot V_\text{os0} \] during \(n \to \infty\) \[ \lim_{n\to \infty} \Delta V_\text{os}[n] = V_\text{os0} \] As expected \[ \lim_{n\to \infty} V_\text{os}[n] =\lim_{n\to \infty} V_\text{os0}-\Delta V_\text{os}[n] = 0 \]

Assuming that begainning from \(\Phi_+\) phase \[ \left\{ \begin{array}{cl} \Delta V_\text{os}[0] &= \frac{I_l[0]-I_r[-1]}{G_m} \\ \left(I_0+\frac{V_\text{os0}-\Delta V_\text{os}[0]}{R_E}\right)\beta &= I_l[0]+I_r[-1] \end{array} \right. \overset{\mathcal{I_r[-1]=0}}{\Longrightarrow} \Delta V_\text{os}[0]=\frac{(I_0R_E+V_\text{os0})\beta}{G_mR_E+\beta} \] With \(I_0=10\mu A\), \(R_E=5k \Omega\), \(V_\text{os0}=20mV\), \(G_m=500\mu S\), \(\beta=0.5\) \[ \left\{ \begin{array}{cl} \Delta V_\text{os}[0] &= 167mV \\ \frac{G_mR_E-\beta}{G_mR_E+\beta} &= 0.667 \end{array} \right. \]

image-20250803231213438

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
DVos0 = 167;  % mV
Vos0 = 20; % mV
Rr = 0.667;

n = 1:1:50;
DVosn_DVos0 = Rr.^n*DVos0;
DVosn_Vos0 = (1-Rr.^n)*Vos0;
DVosn = DVosn_DVos0 + DVosn_Vos0;

plot(n, DVosn_DVos0,'--r', LineWidth=2);
hold on
plot(n, DVosn_Vos0, '--g', LineWidth=2);
plot(n, DVosn, 'b', LineWidth=3);
plot(-5:1:55, ones(1,61)*Vos0, '--k', LineWidth=2)

grid on;
xlim([-5, 55]);ylim([-5, 120]);
xlabel('n', FontSize=16); ylabel('mV', FontSize=16);
legend('$\Delta V_{os}[0]$ decaying','$V_{os0}$ decaying','$\Delta V_{os}[n]$', '$V_{os0}$', 'Interpreter','latex', fontsize=16)

reference

C. C. Enz and G. C. Temes, "Circuit techniques for reducing the effects of op-amp imperfections: autozeroing, correlated double sampling, and chopper stabilization," in Proceedings of the IEEE, vol. 84, no. 11, pp. 1584-1614, Nov. 1996, doi: 10.1109/5.542410. [http://www2.ing.unipi.it/~a008309/mat_stud/MIXED/archive/2019/Articles/Offset_canc_Enz_Temes_96.pdf]

Kofi Makinwa. Precision Analog Circuit Design: Coping with Variability, [https://youtu.be/nA_DZtRqrTQ?si=6uyOpJhdnYm3iG9d] [https://youtu.be/uwRpP20Lprc?si=SGPta86jRCdECSob]

Chung-chun Chen, Why Design Challenge in Chopping Offset & Flicker Noise? [https://youtu.be/ydjca2KrXgc?si=2raCIB99vXriMPsq]

—, Why Needs A Low Ripple after Chopping Amplifier for A Very Low DC Offset & Flicker Noise? [https://youtu.be/y7TzJtHE7IA?si=kUeP_ESofVxp3IT_]

Qinwen Fan, Evolution of precision amplifiers

Kofi Makinwa, ISSCC 2007 Dynamic-Offset Cancellation Techniques in CMOS [https://picture.iczhiku.com/resource/eetop/sYkywlkpwIQEKcxb.pdf]

Axel Thomsen, Silicon Laboratories ISSCC2012 T8: "Managing Offset and Flicker Noise" [slides,transcript]

CC Chen. Why Dynamic Offset or Mismatch Cancellation with Auto-zeroing Technique? [https://youtu.be/PQJwzd1tyO0]

—. Why Dynamic Offset or Mismatch Cancellation with Chopping Technique? [https://youtu.be/x5FS8jEKu_g]

—. Why Design Challenge in Chopping Offset & Flicker Noise? [https://youtu.be/ydjca2KrXgc]

—. Why Needs A Low Ripple after Chopping Amplifier for A Very Low DC Offset & Flicker Noise? [https://youtu.be/y7TzJtHE7IA]