Delta-Sigma Modulator

Posted on Edited on In

Classification

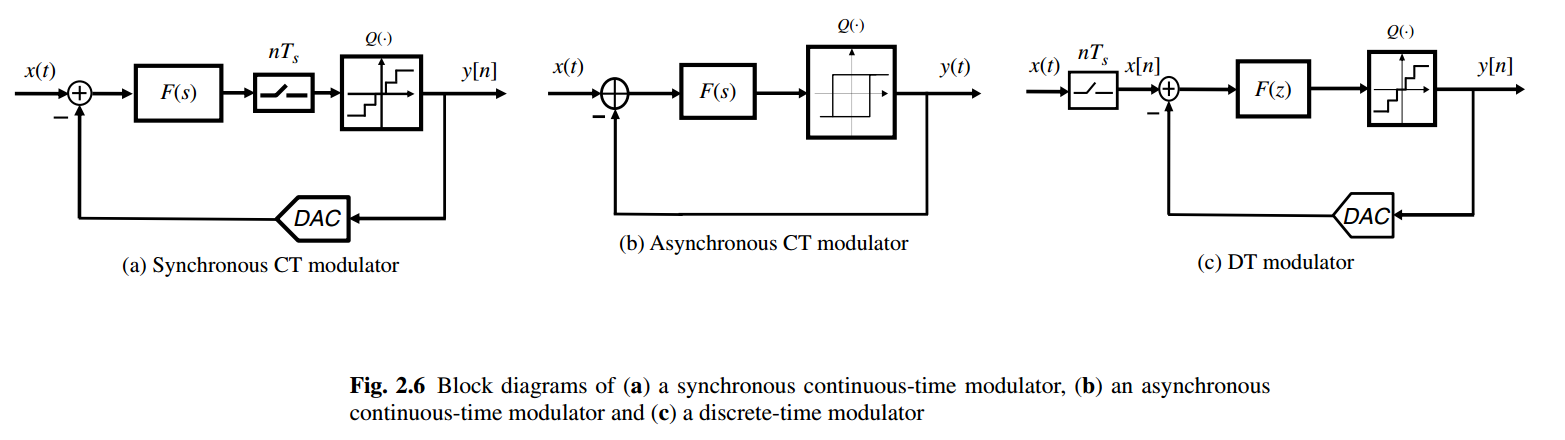
  • Continuous-Time (CT) Analog Modulator
    • Sampled Quantizer: Synchronous Modulator
    • Unsampled Quantizer: Asynchronous Modulator
  • Discrete-Time (DT) Analog Modulator
    • The main application is in \(\Delta\Sigma\) ADCs
  • Discrete-Time Digital Modulators (DDSM)
    • Single Quantizer DDSMs - output feedback
    • Error feedback modulators (EFM) - error feedback
    • Multi stAge noise SHaping (MASH)

image-20250903210531360

image-20250611074830238

"Quantizers" and "truncators", and "integrators" and "accumulators" are used in delta-sigma ADCs and DACs, respectively

P. Kiss, J. Arias and Dandan Li, "Stable high-order delta-sigma DACS," 2003 IEEE International Symposium on Circuits and Systems (ISCAS), Bangkok, 2003 [https://www.ele.uva.es/~jesus/analog/tcasi2003.pdf]

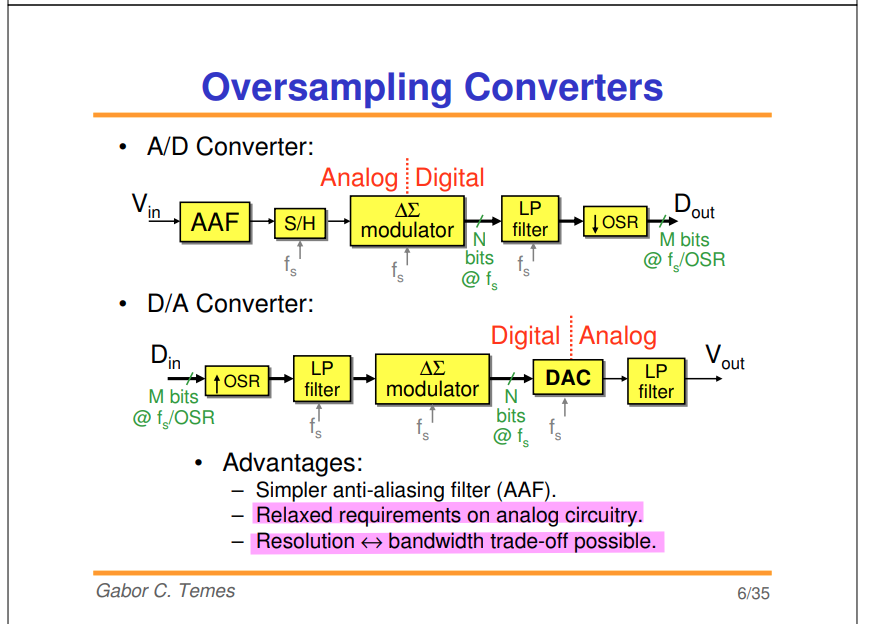
Oversampling

image-20250611232612319

David Johns and Ken Martin. Oversampling Converters [https://www.eecg.toronto.edu/~johns/ece1371/slides/14_oversampling.pdf]

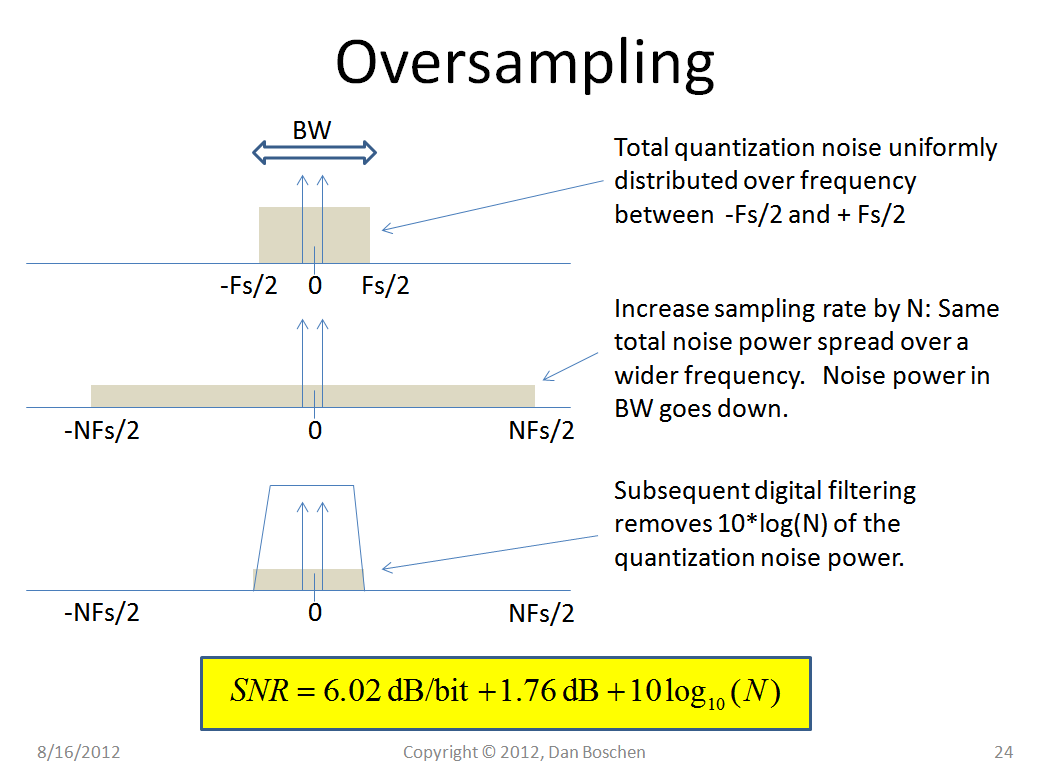
Over Sampling

Nyquist sampling theorem @signal: no aliasing, signal remain the same

noise folding @noise: same total noise power spread over a wider frequency

[https://dsp.stackexchange.com/a/40261/59253]

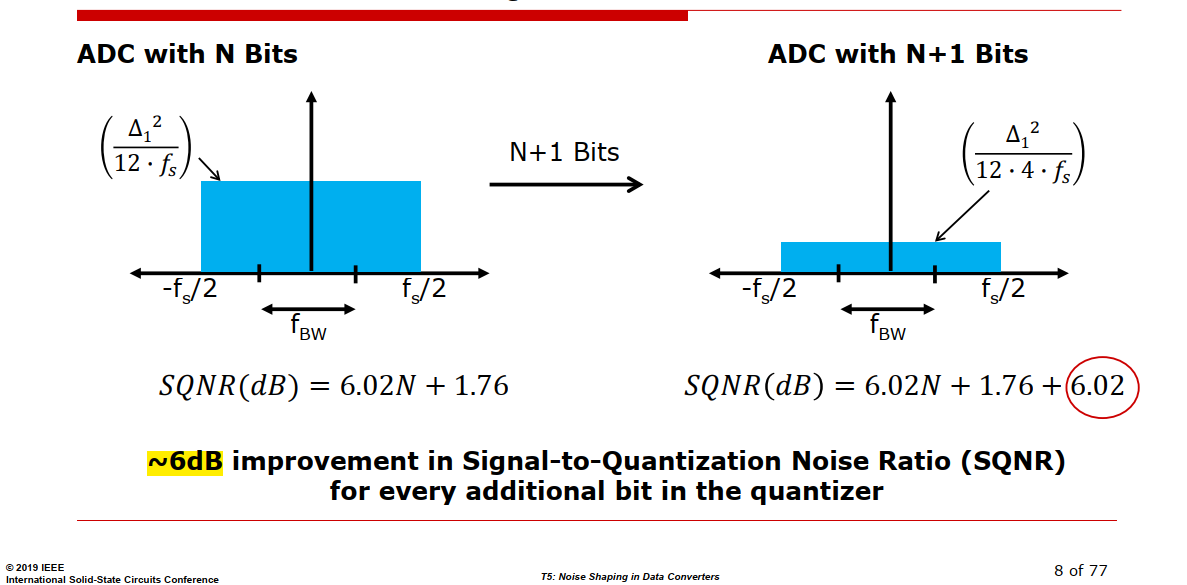
image-20250629215715378

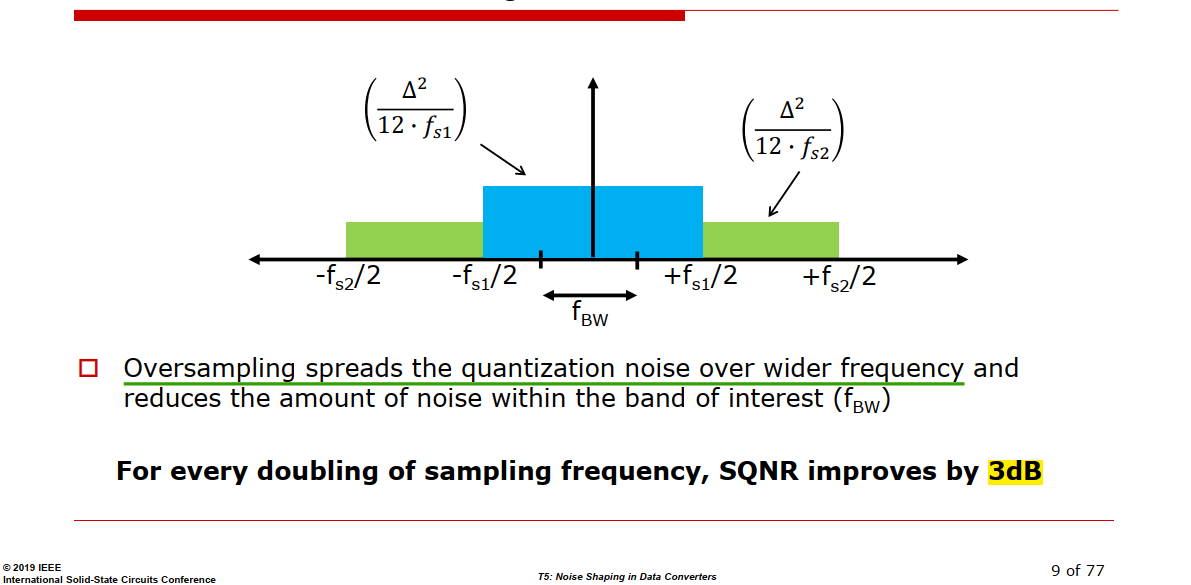
image-20250629215830077

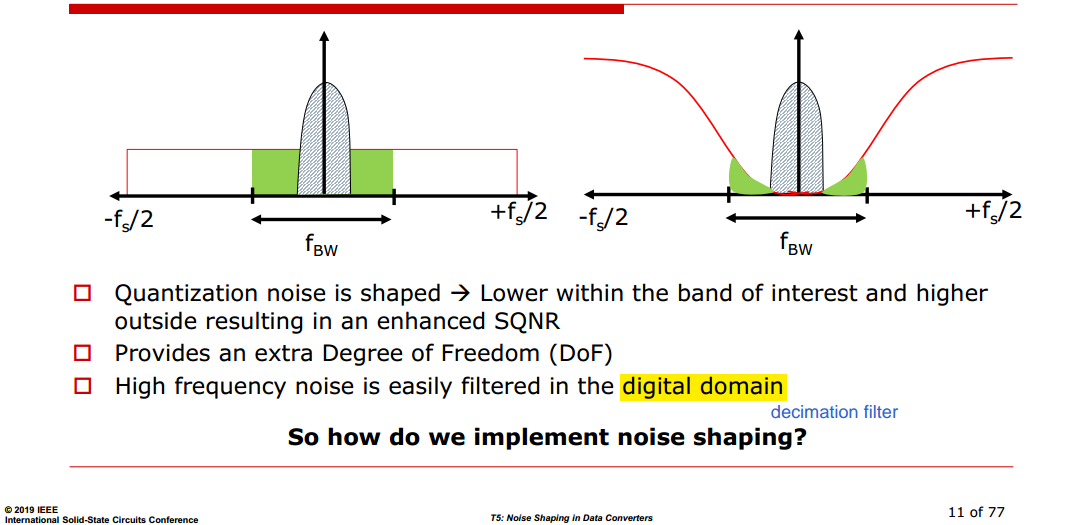
Noise Shaping

image-20250629232343017

image-20250629232453811

1
2
3
4
5
6
7
8
9
10
11
[h1, w1] = freqz([1 -1], 1);
[h2, w2] = freqz([1 -2 1], 1);

plot(w1/2/pi, abs(h1), LineWidth=3)
hold on
plot(w2/2/pi, abs(h2), LineWidth=3)
grid on
legend('MOD1', 'MOD2')
xlabel('fs')
ylabel('mag')
title('NTF of MOD1 & MOD2')

image-20250824151828263

SQNR improvement

In general, for an \(l\)th order modulator with \(\text{NTF}(z) = (1 − z^{−1})^l\), the SQNR increases by \((6l + 3)\) dB for every doubling of the OSR, which provides \(l+0.5\) extra bits resolution

without the delta-sigma loop

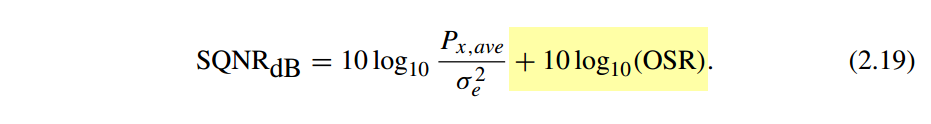
image-20250823220900699

\(10\log (2) \approx 3\)dB

first order delta-sigma modulator

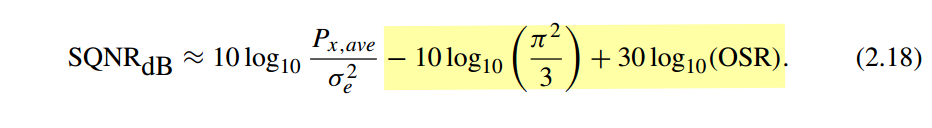
image-20250823220842529

\(30\log (2) \approx 9\)dB

second order delta-sigma modulator

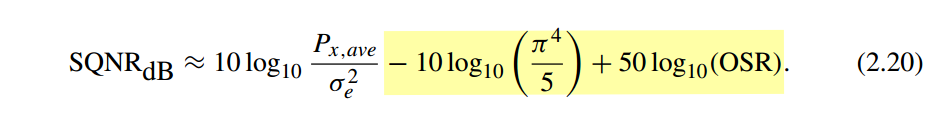
image-20250823220922480

\(50\log (2) \approx 15\)dB

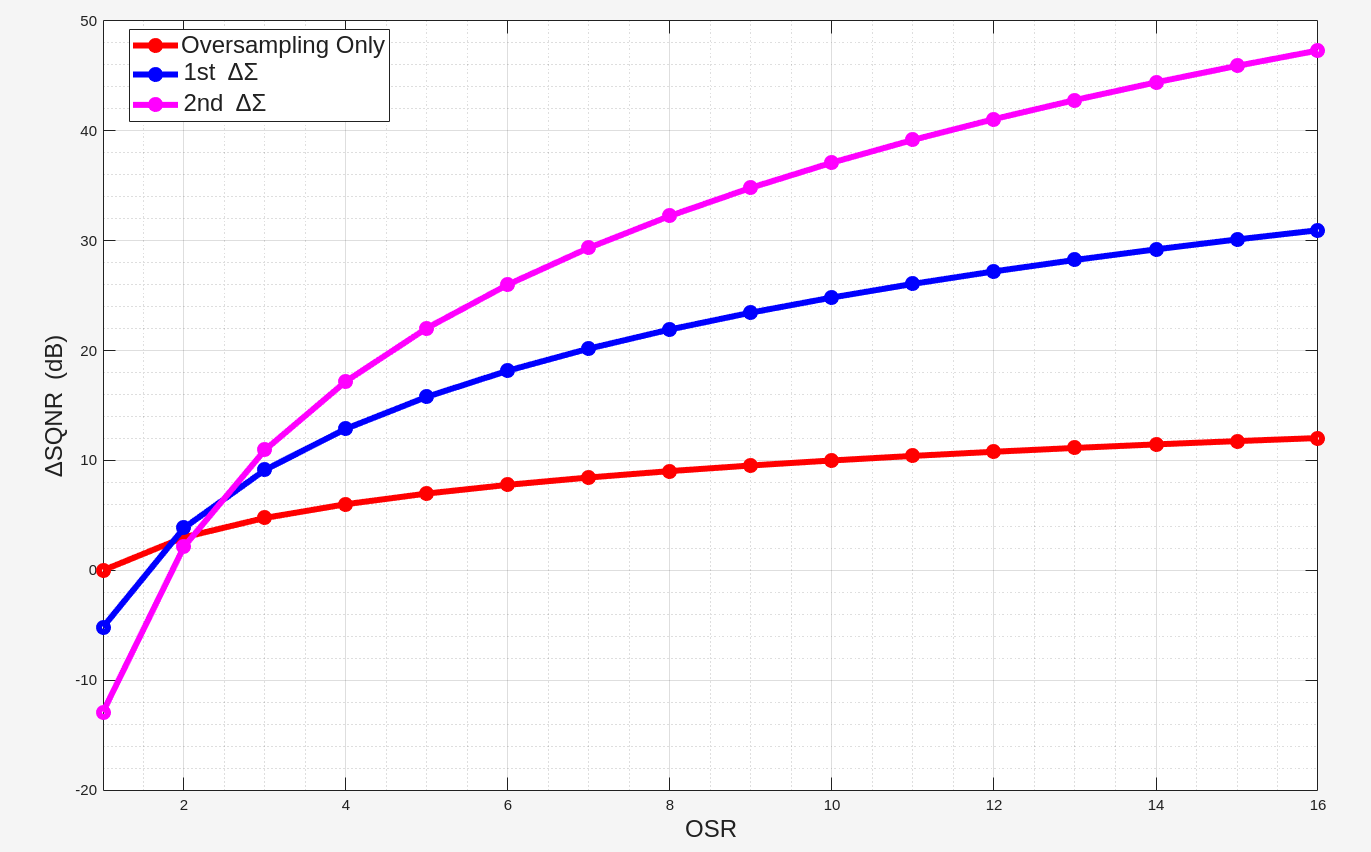
image-20250823224500839

1
2
3
4
5
6
7
8
9
10
11
12
13
14
OSR= linspace(1,16,16);

SQNR_ovonly_delta = 10*log10(OSR);
SQNR_1st_delta = -10*log10(pi^2/3) + 30*log10(OSR);
SQNR_2st_delta = -10*log10(pi^4/5) + 50*log10(OSR);

plot(OSR, SQNR_ovonly_delta,'ro-', LineWidth=4);
hold on
plot(OSR, SQNR_1st_delta,'bo-', LineWidth=4);
plot(OSR, SQNR_2st_delta,'mo-', LineWidth=4);
grid on; grid minor;
xlim([1 16]); ylim([-20 50]);
xlabel('OSR', FontSize=16); ylabel('\DeltaSQNR (dB)', FontSize=16);
legend('Oversampling Only', '1st \Delta\Sigma', '2nd \Delta\Sigma', fontsize=16)

TI. ADC12EU050 Continuous-Time Sigma-Delta ADCs [https://www.ti.com/lit/an/snaa098/snaa098.pdf]

image-20250906192735041

where \(N\) is the number of bits in the output, \(M\) is known as the over-sampling ratio, \(L\) is loop orders

Quantizer Bits & ENOB

without the delta-sigma loop

image-20250921132712308

image-20250921102250022

image-20250921124756085

High-Order \(\Delta\Sigma\) Modulators

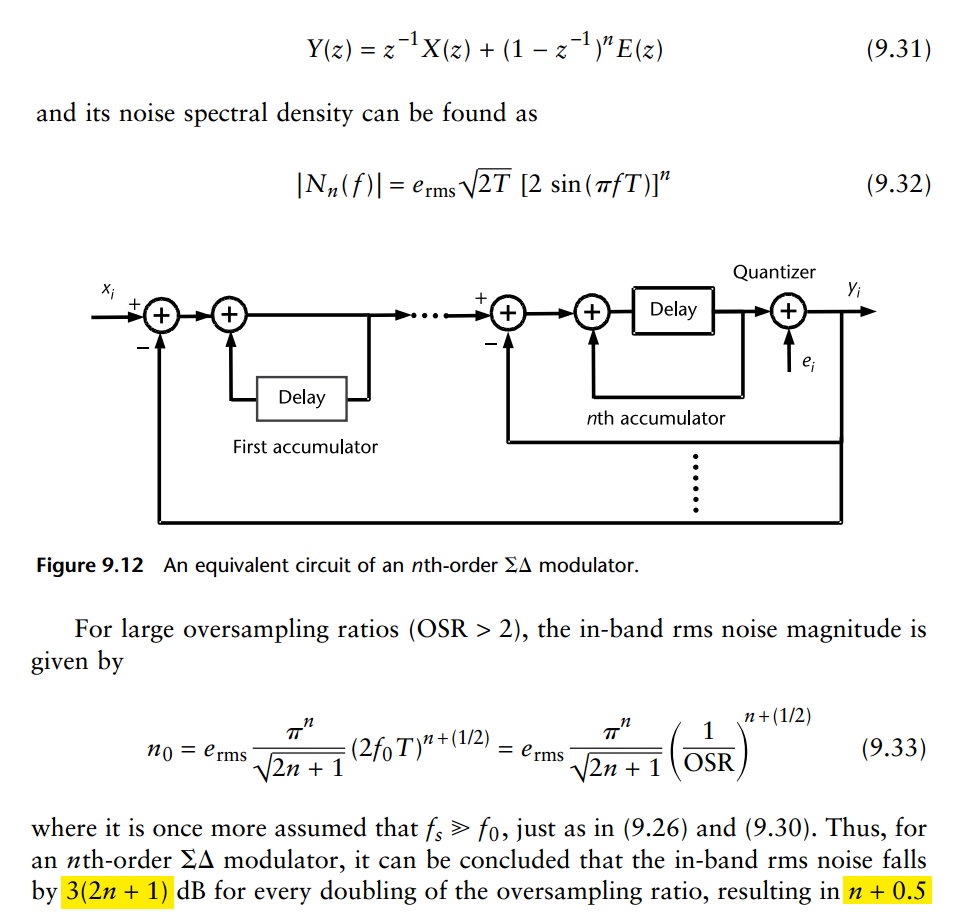
image-20250921133840404

image-20250921134001793

image-20250921134051906

image-20250921134312753

The greater the number of quantizer levels, the smaller quantization error

image-20250824081318669

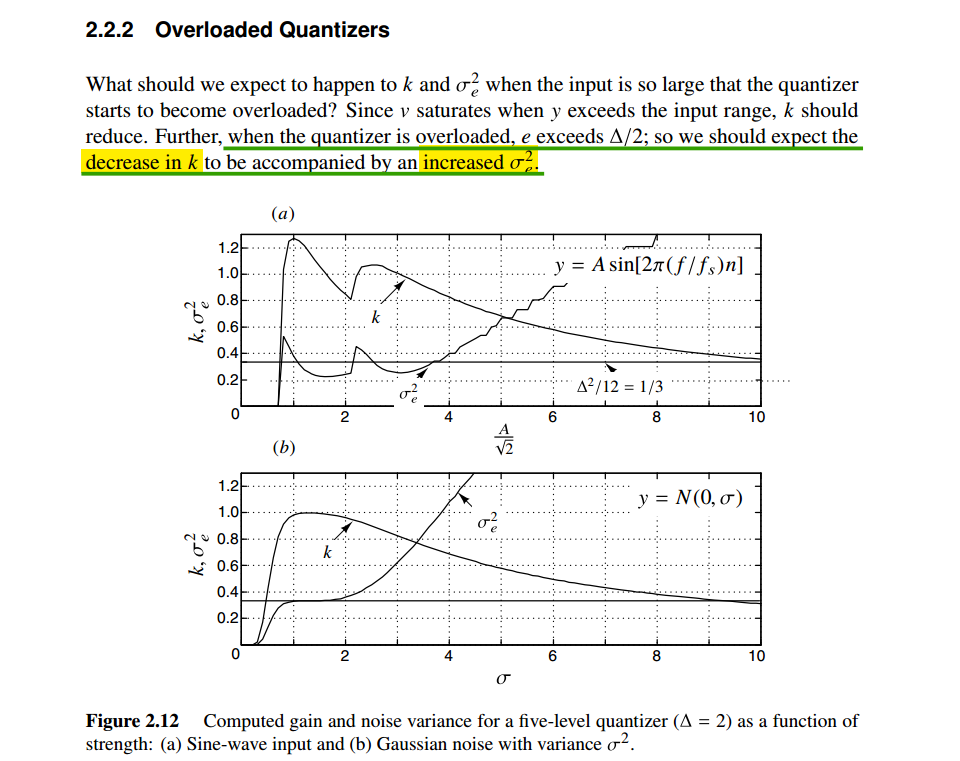
Quantizer overload

image-20250905062939783

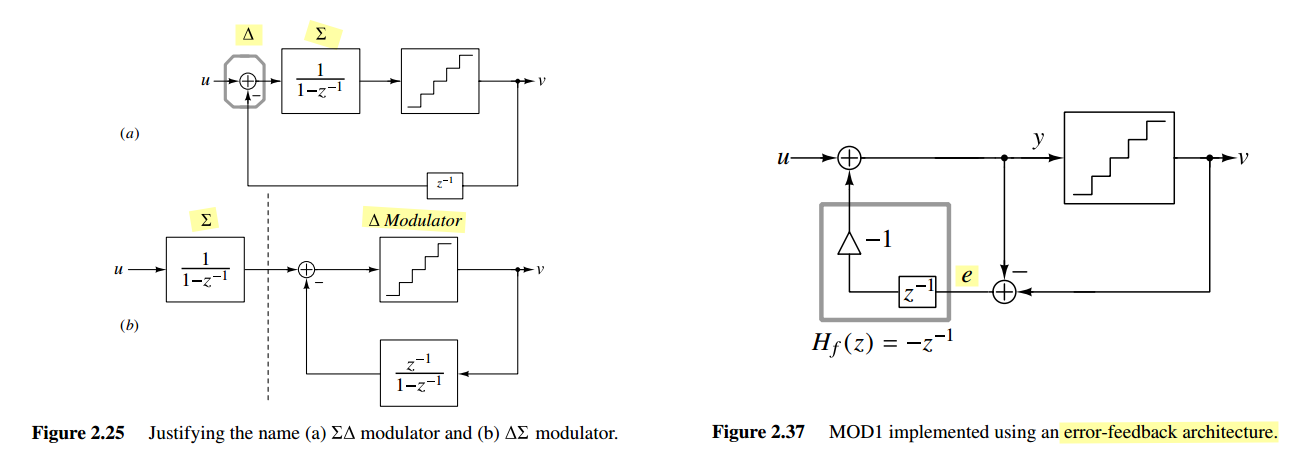
\(\Delta \Sigma\) vs. \(\Delta\) modulation

  • \(\Delta \Sigma\) modulators, and other noise-shaping modulators, change the spectrum of the noise but leave the signal unchanged

  • \(\Delta\) modulators and other signal-predicting modulators shape the spectrum of the modulated signal but leave the quantization noise unchanged at the receiver

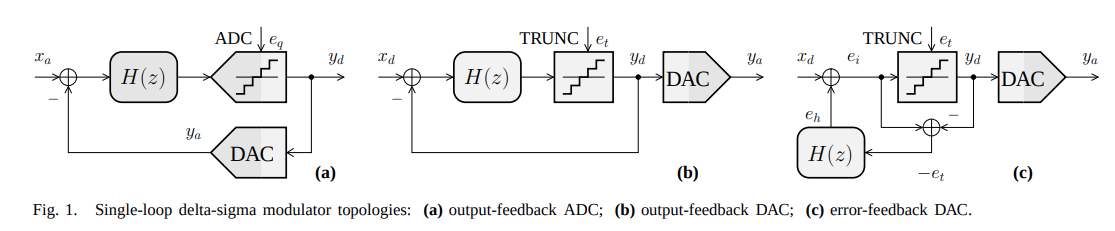
output vs. error-feedback

The error-feedback architecture is problematic for analog implementation, since it is sensitive to variations of its parameters (subtractor realization)

  • The error-feedback structure is thus of limited utility in \(\Delta \Sigma\) ADCs
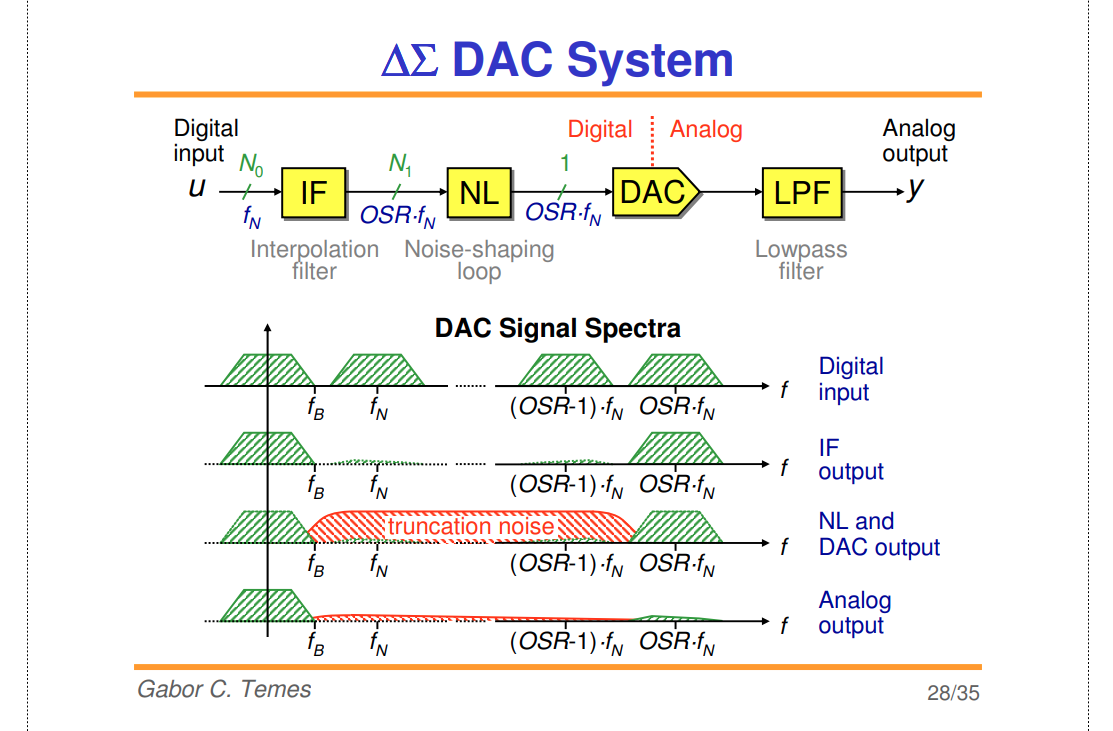
  • The error-feedback structure is very useful and applied in digital loops required in \(\Delta \Sigma\) DACs

ADC

image-20250618203604863

image-20250618203636417

DAC

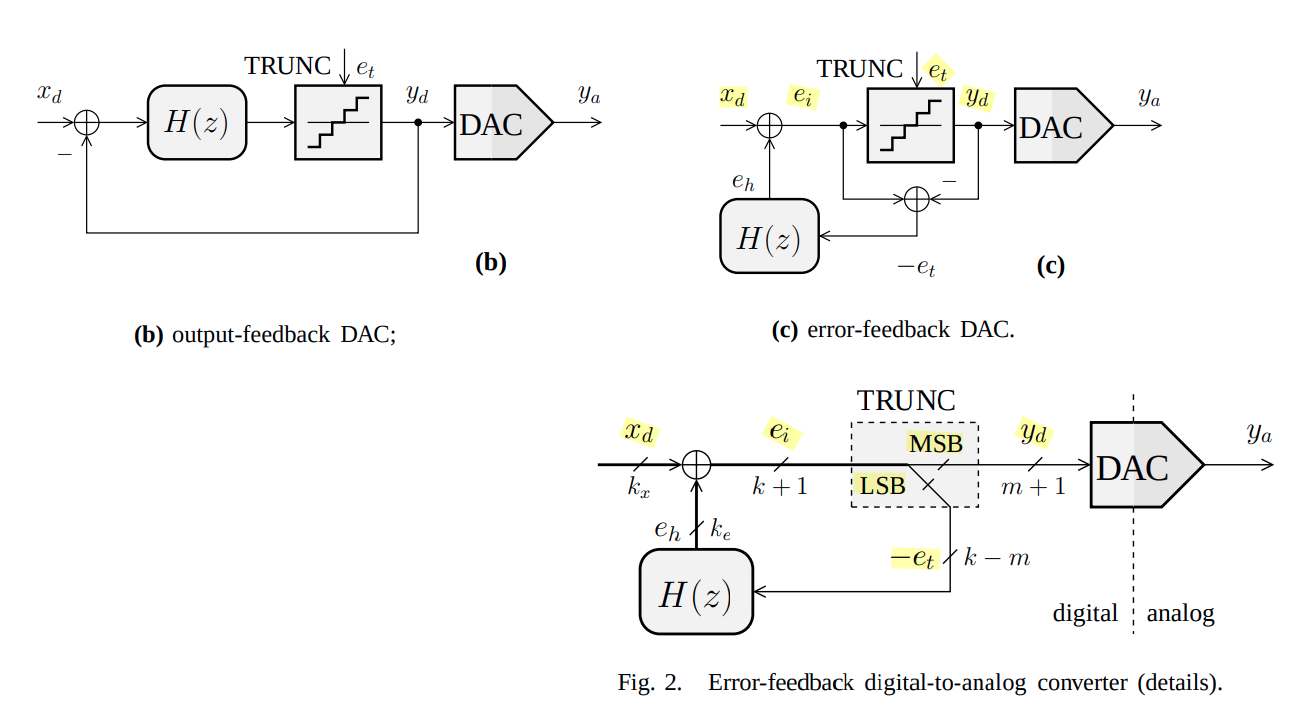
image-20250617223537672

P. Kiss, J. Arias and Dandan Li, "Stable high-order delta-sigma DACS," 2003 IEEE International Symposium on Circuits and Systems (ISCAS), Bangkok, 2003 [https://www.ele.uva.es/~jesus/analog/tcasi2003.pdf]

output-feedback

img

[https://www.linkedin.com/posts/danboschen_signalprocessing-dsp-pythonforengineers-activity-7345777588746788866-SprG?utm_source=share&utm_medium=member_desktop&rcm=ACoAAD-cuiIBDJ62eh9q3qTSSdslYXr-XMd8TGw]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
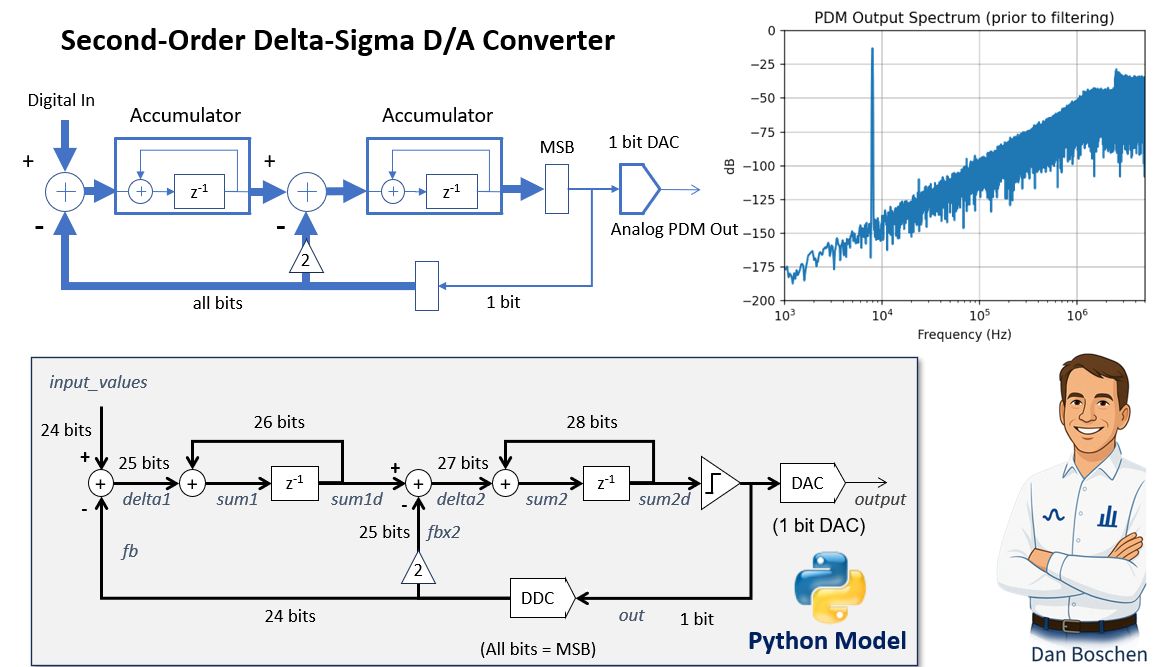
// https://github.com/hamsternz/second_order_sigma_delta_DAC

`timescale 1ns / 1ps
module second_order_dac(
  input wire i_clk,
  input wire i_res,
  input wire i_ce,
  input wire [15:0] i_func, 
  output wire o_DAC
);

  reg this_bit;
 
  reg [19:0] DAC_acc_1st;
  reg [19:0] DAC_acc_2nd;
  reg [19:0] i_func_extended;
   
  assign o_DAC = this_bit;

  always @(*)
     i_func_extended = {i_func[15],i_func[15],i_func[15],i_func[15],i_func};
    
  always @(posedge i_clk or negedge i_res)
    begin
      if (i_res==0)
        begin
          DAC_acc_1st<=16'd0;
          DAC_acc_2nd<=16'd0;
          this_bit = 1'b0;
        end
      else if(i_ce == 1'b1) 
        begin
          if(this_bit == 1'b1)
            begin
              DAC_acc_1st = DAC_acc_1st + i_func_extended - (2**15);
              DAC_acc_2nd = DAC_acc_2nd + DAC_acc_1st     - (2**15);
            end
          else
            begin
              DAC_acc_1st = DAC_acc_1st + i_func_extended + (2**15);
              DAC_acc_2nd = DAC_acc_2nd + DAC_acc_1st + (2**15);
            end
          // When the high bit is set (a negative value) we need to output a 0 and when it is clear we need to output a 1.
          this_bit = ~DAC_acc_2nd[19];
        end
    end
endmodule

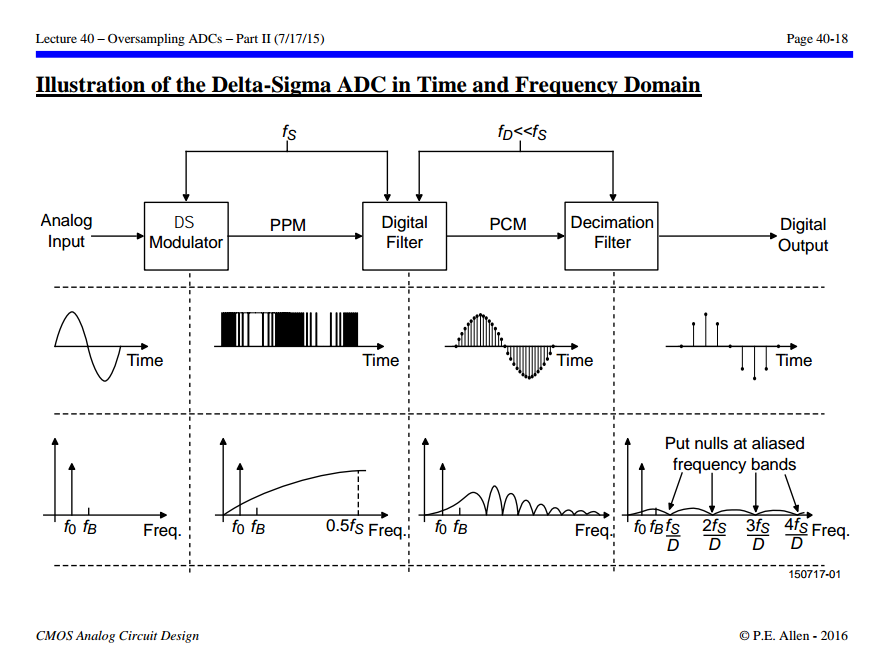
Time and Frequency Domain

image-20250627193435726

\(M \gt N\)

[https://web.engr.oregonstate.edu/~temes/ece627/Lecture_Notes/Intro_to_Delta_Sigma_Data_Converters.pdf]

Chun-Hsien Su ( 蘇純賢). Fundamentals of Sigma-Delta Data Converters,July, 2006 [pdf]

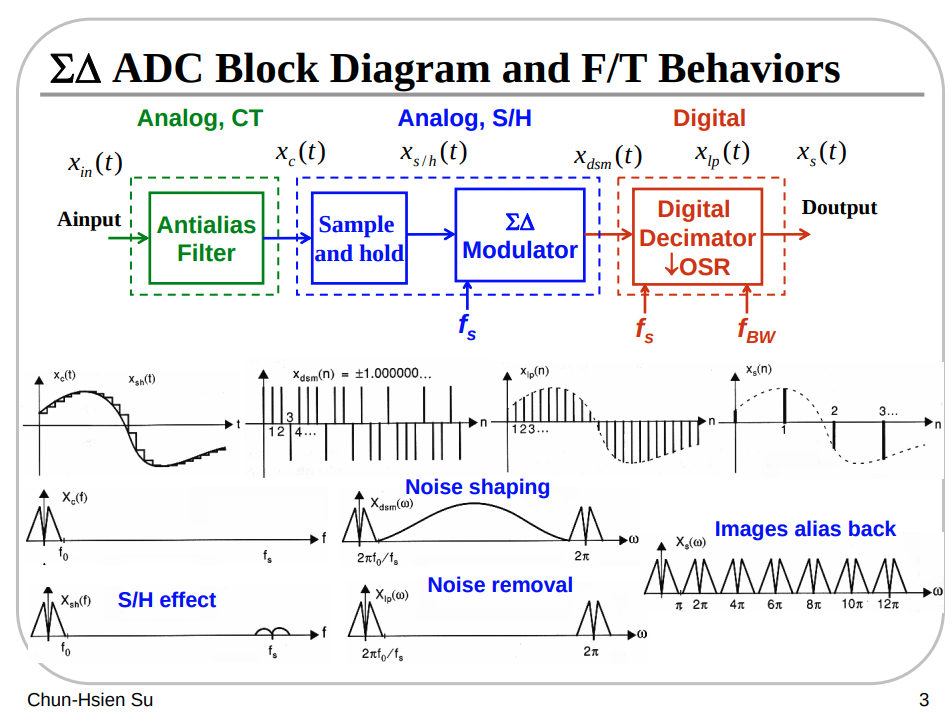
image-20250809235244362

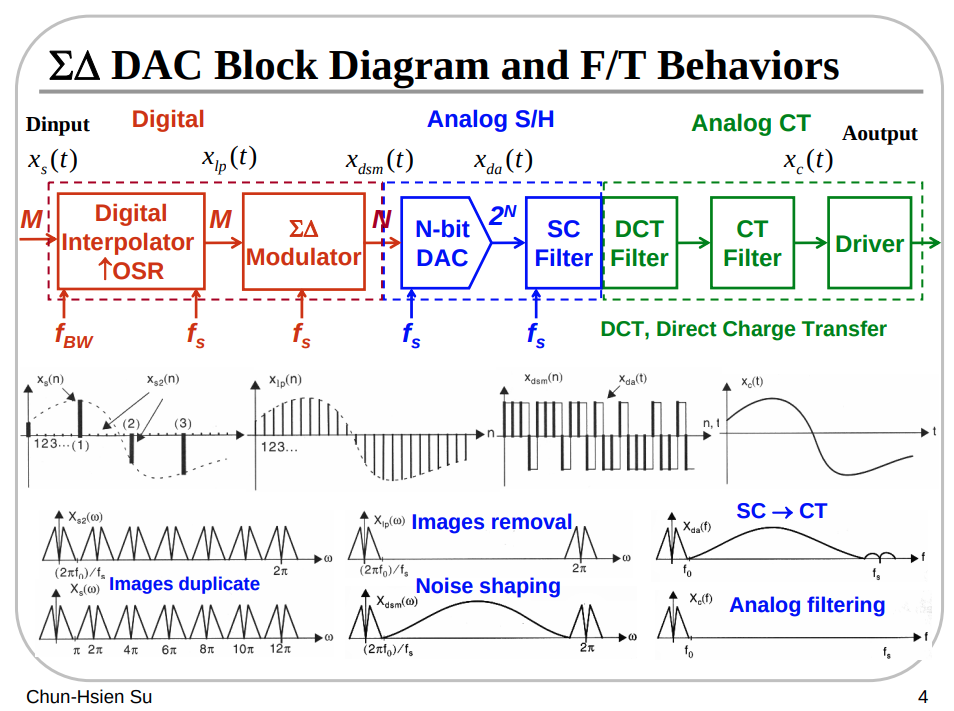
image-20250809235311542

ADC

image-20250611234653738

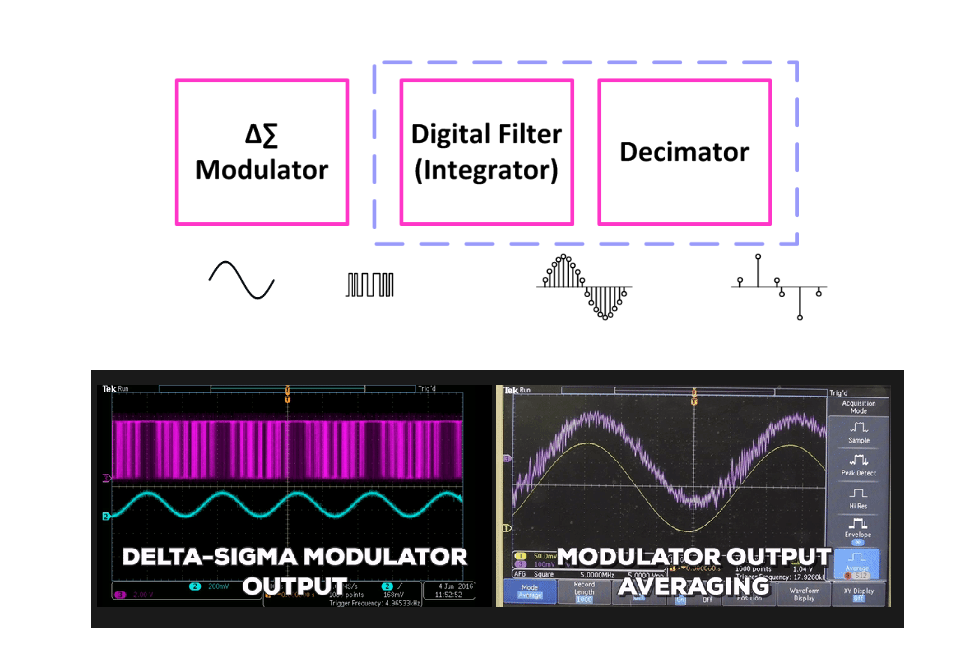
image-20250612000925089

hackaday. Tearing Into Delta Sigma ADC’s [https://hackaday.com/2016/07/07/tearing-into-delta-sigma-adcs-part-1/]

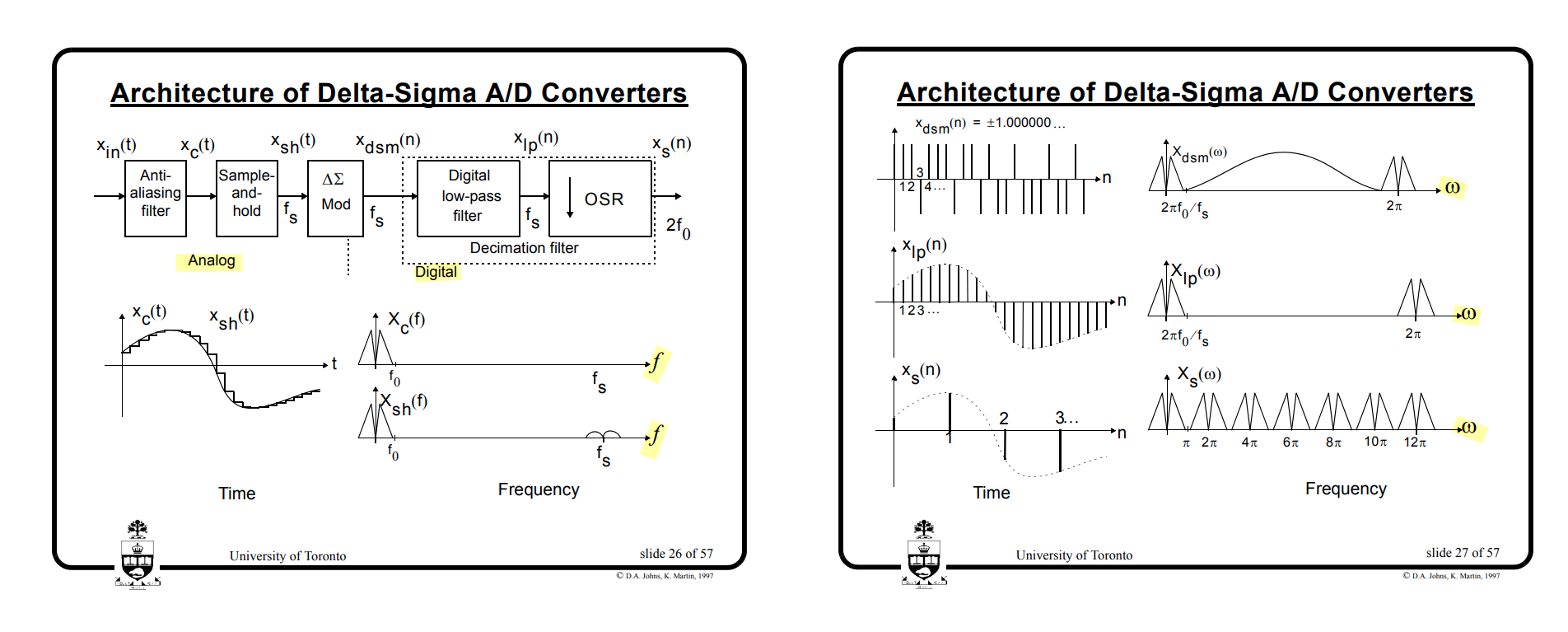
image-20250617234727838

DAC

an interpolation filter effectively up-samples its low-rate input and lowpass-filters the resulting high-rate data to produce a high-rate output devoid of images

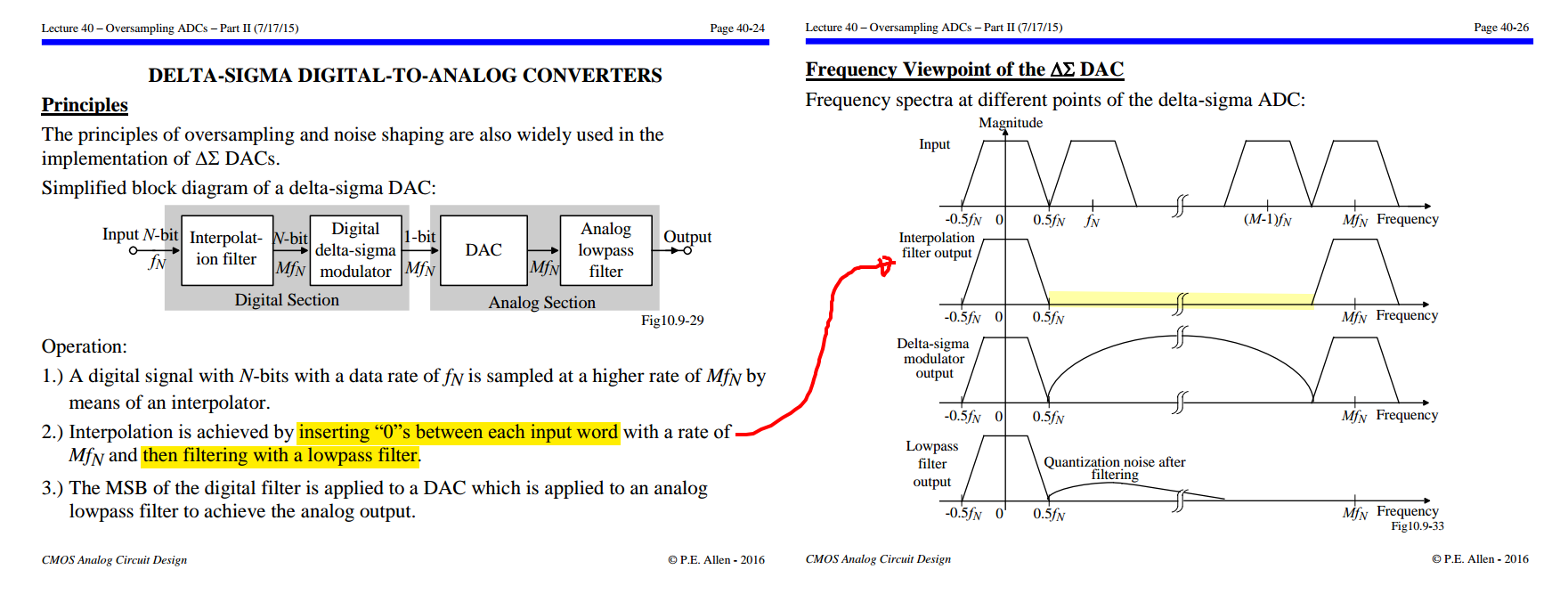
image-20250612000423191

P.E. Allen -CMOS Analog Circuit Design: Lecture 39 – Oversampling ADCs – Part I (6/26/14) [https://aicdesign.org/wp-content/uploads/2018/08/lecture39-140626.pdf]

P.E. Allen -CMOS Analog Circuit Design: Lecture 40 – Oversampling ADCs – Part II (7/17/15) [https://aicdesign.org/wp-content/uploads/2018/08/lecture40-150717.pdf]

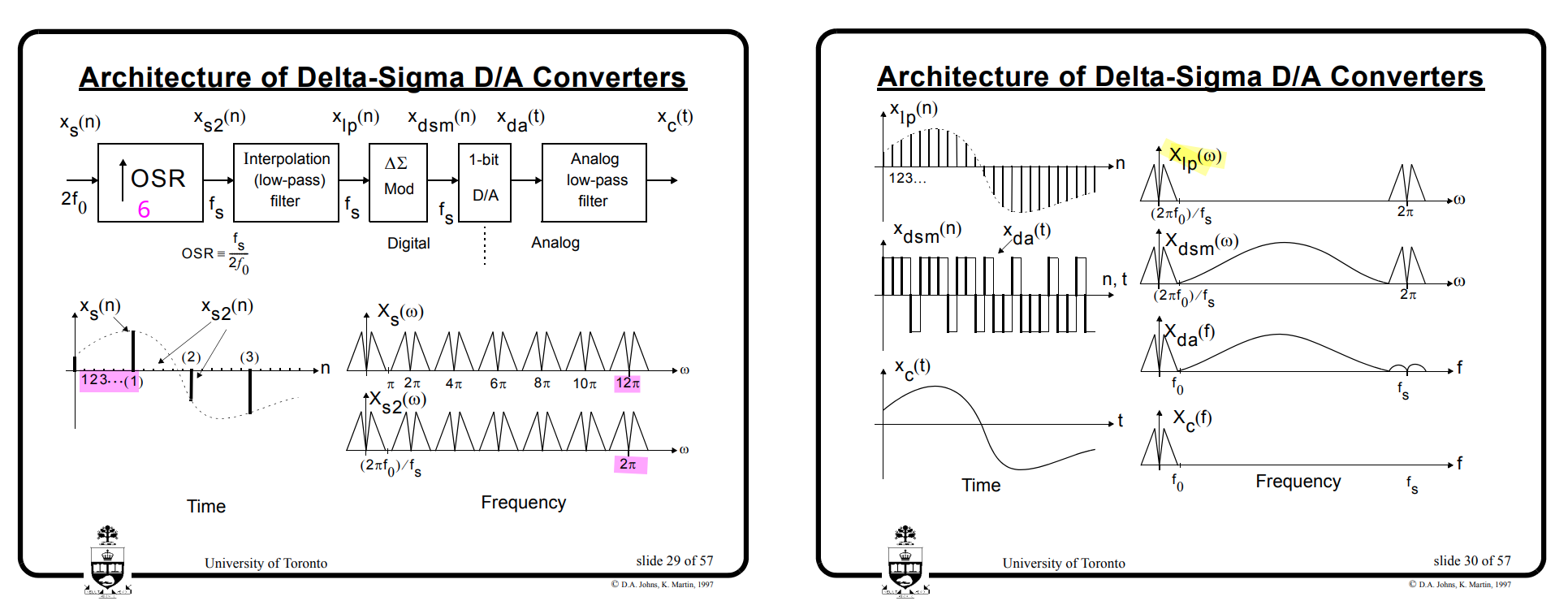
image-20250720201944707

David Johns and Ken Martin. Oversampling Converters [https://www.eecg.toronto.edu/~johns/ece1371/slides/14_oversampling.pdf]

image-20250627194351778

[https://web.engr.oregonstate.edu/~temes/ece627/Lecture_Notes/Intro_to_Delta_Sigma_Data_Converters.pdf]

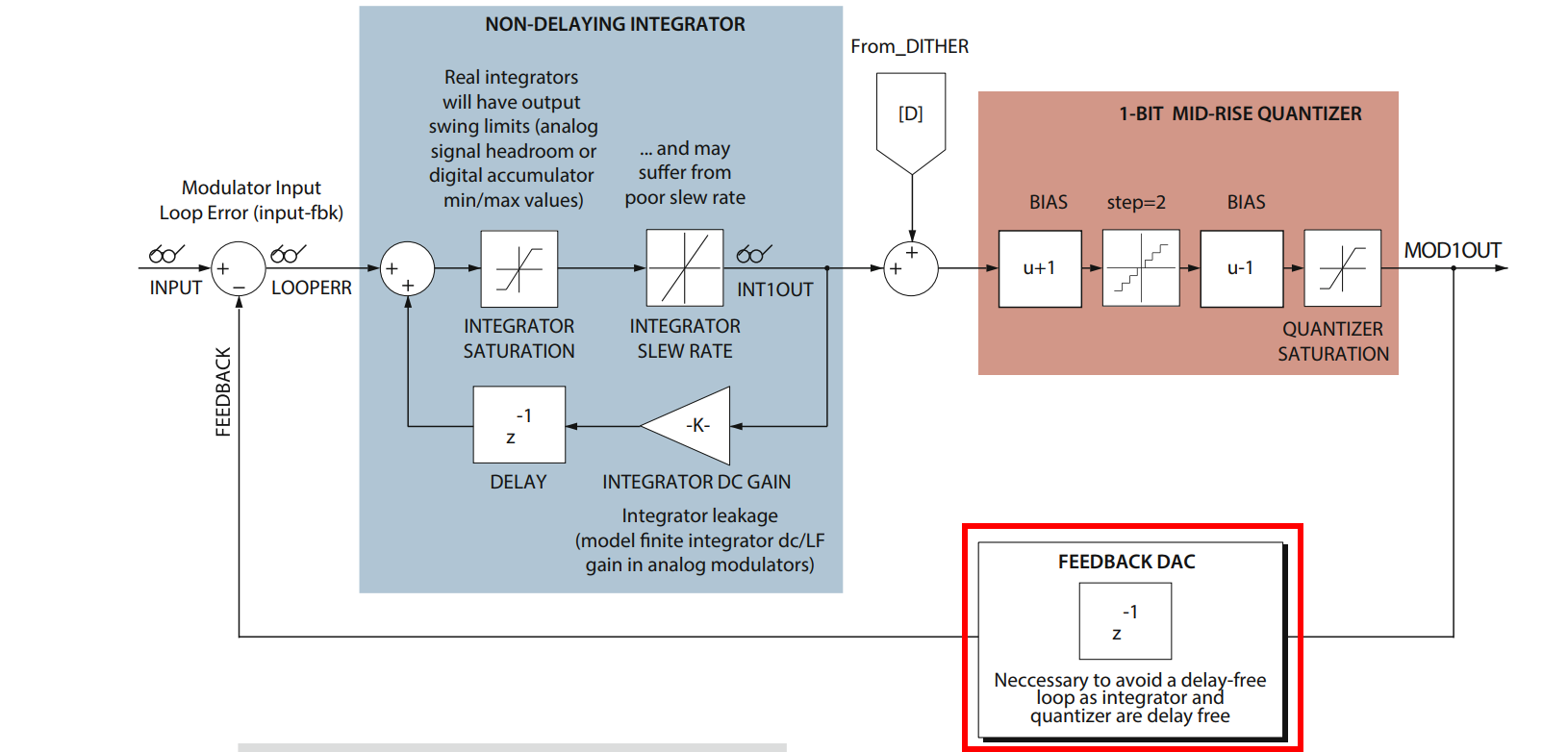
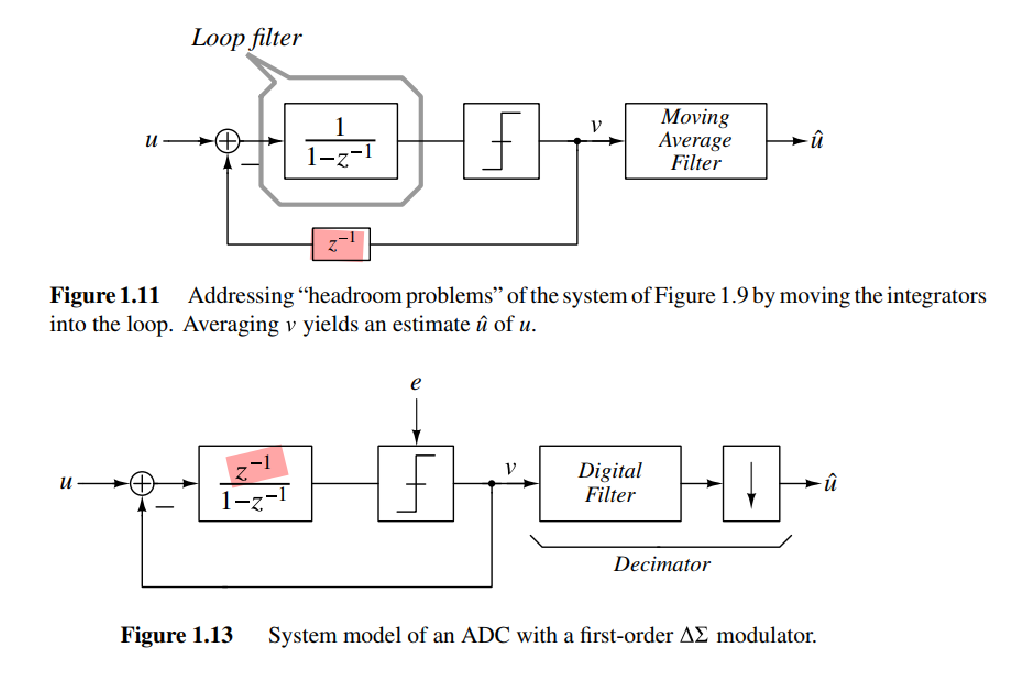
No delay-free loops

Any such physically feasible device will take a finite time to operate – in other words, the quantized output will only be available a small time after the quantizer has "looked" at the input - insert a one-sample delay

image-20250617231014547

there cannot be a "delay free loop" is a common idea in sequential digital state machine design

image-20241128232040924

Both integrator and quantizer are delay free

NTF realizability criterion: No delay-free loops in the modulator

image-20241128233022231

linear settling & GBW of amplifier

TODO 📅

Switched capacitor has been the common realization technique of discrete-time (DT) modulators, and in order to achieve a linear settling, the sampling frequency used in these converters needs to be significantly lower than the gain bandwidth product (GBW) of the amplifiers.

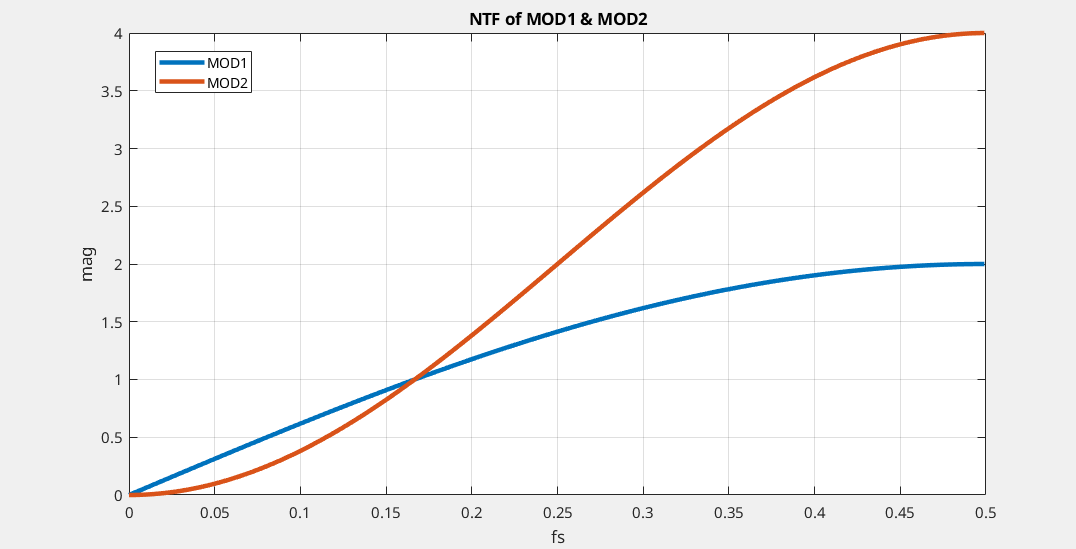
MOD1 & MOD2

MOD1: first-order noise-shaped converter (\(\Delta\Sigma\) modulator)

MOD2: second-order noise-shaped converter (\(\Delta\Sigma\) modulator)

MOD1

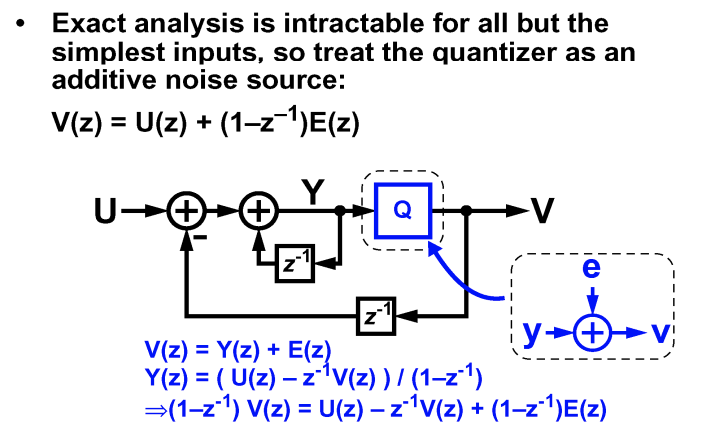image-20241005120659945 \[ V(z) = U(z) +(1-z^{-1})E(z) \]

  • A binary DAC (and hence a binary modulator) is inherently linear
  • With a CT loop filter, MOD1 has inherent anti-alising

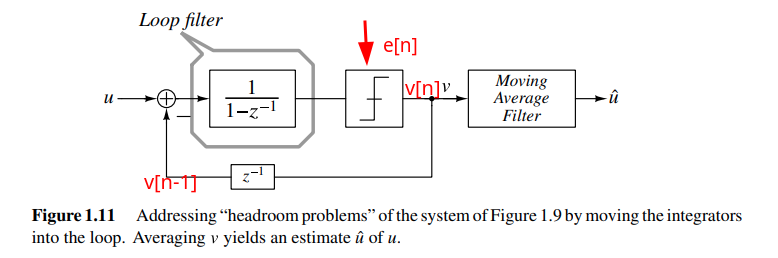image-20241005202024498 \[\begin{align} v[1] &= u - (0) + e[1] \\ v[2] &= 2u - (v[1]) + e[2] \\ v[3] &= 3u - (v[1]+v[2]) + e[3] \\ v[4] &= 4u - (v[1]+v[2]+v[3]) + e[4] \end{align}\]

That is \[ v[n] = nu - \sum_{k=1}^{n-1}v[k] + e[n] \] Therefore, we have \(v[n-1] = (n-1)u - \sum_{k=1}^{n-2}v[k] + e[n-1]\), then \[\begin{align} v[n] &= nu - \sum_{k=1}^{n-1}v[k] + e[n] \\ &= u + \left((n-1)u - \sum_{k=1}^{n-2}v[k]\right) - v[n-1] + e[n] \\ &= u + v[n-1] - e[n-1] -v[n-1] + e[n] \\ &= u + e[n] - e[n-1] \end{align}\]

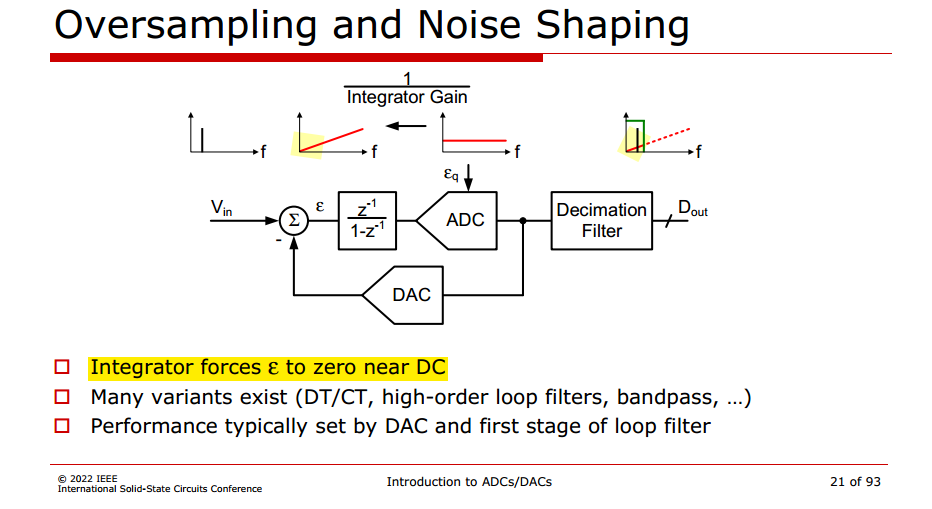
image-20250524215712688

Dout, the low frequency component of ADC out is same with Vin

MOD2

[https://web.engr.oregonstate.edu/~temes/ece627/Lecture_Notes/2nd_Higher_Order.pdf]

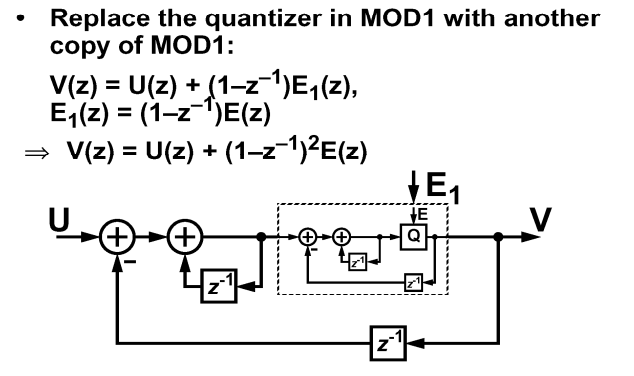
image-20241005160203074

MOD1 with DC Excitation

TODO 📅

Mismatch Shaping

image-20241112220458335

Data-Weighted Averaging (DWA)

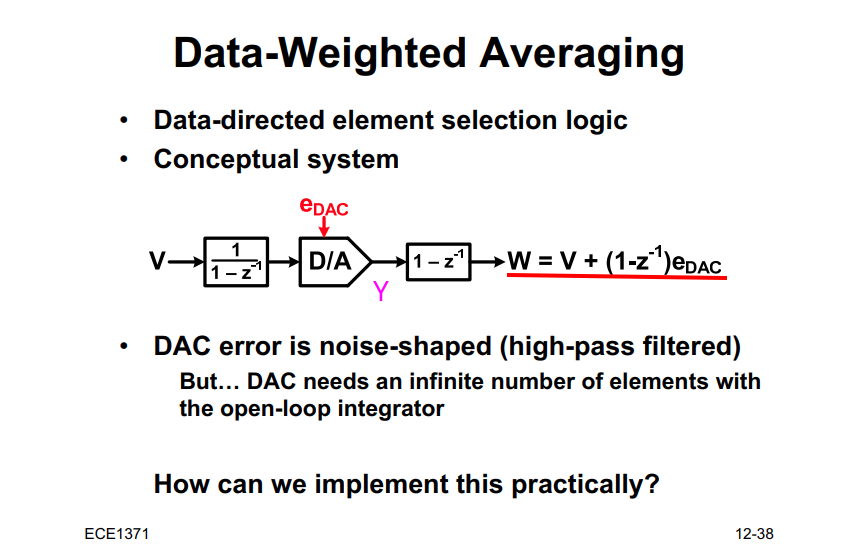image-20241113000942025 \[\begin{align} \sum_{i=0}^{n}v[i] + e_\text{DAC}[n] &= y[n] \\ \sum_{i=0}^{n-1}v[i] + e_\text{DAC}[n-1] &= y[n-1] \end{align}\]

and we have \(w[n] = y[n] - y[n-1]\), then \[ w[n] = v[n] + e_\text{DAC}[n] - e_\text{DAC}[n-1] \] i.e. \[ W = V + (1-z^{-1})e_\text{DAC} \]

Element Rotation:

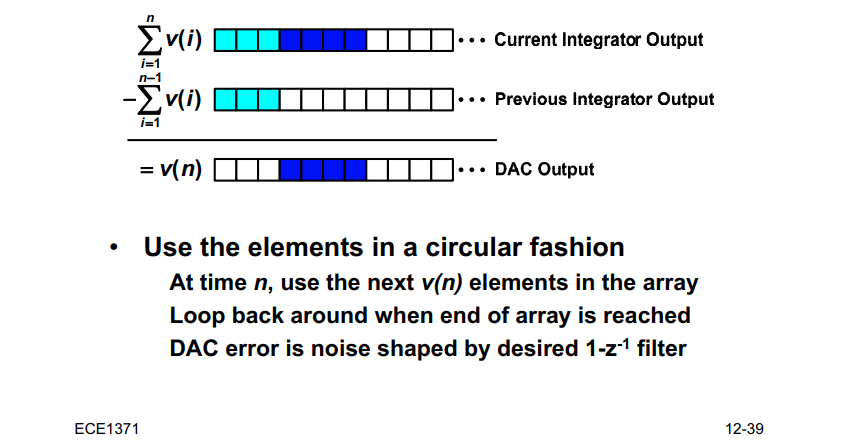
image-20241112233059745

[http://individual.utoronto.ca/schreier/lectures/12-2.pdf], [http://individual.utoronto.ca/trevorcaldwell/course/Mismatch.pdf]

integrator leakage

When the integrator includes leakage (\(\alpha\))

\[ x[n-1] + \alpha y[n-1] = y[n] \]

then, \[ \frac{Y}{X} = \frac{z^{_1}}{1-\alpha z^{-1}} \]

reference

Pavan, Shanthi, Richard Schreier, and Gabor Temes. (2016). Understanding Delta-Sigma Data Converters. 2nd ed. Wiley.

Norsworthy, Steven R., Richard Schreier, Gábor C. Temes and Ieee Circuits. “Delta-sigma data converters : theory, design, and simulation.” (1997).

Horowitz, P., & Hill, W. (2015). The art of electronics (3rd ed.). Cambridge University Press. [pdf]

John Rogers, Calvin Plett, and Foster Dai. 2006. Integrated Circuit Design for High-Speed Frequency Synthesis (Artech House Microwave Library). Artech House, Inc., USA. [pdf]

R. Schreier, ISSCC2006 tutorial: Understanding Delta-Sigma Data Converters

Shanthi Pavan, ISSCC2013 T5: Simulation Techniques in Data Converter Design [https://www.nishanchettri.com/isscc-slides/2013%20ISSCC/TUTORIALS/ISSCC2013Visuals-T5.pdf]

Bruce A. Wooley , 2012, "The Evolution of Oversampling Analog-to-Digital Converters" [https://r6.ieee.org/scv-sscs/wp-content/uploads/sites/80/2012/06/Oversampling-Wooley_SCV-ver2.pdf]

Venkatesh Srinivasan, ISSCC 2019 T5: Noise Shaping in Data Converters

B. Razavi, "The Delta-Sigma Modulator [A Circuit for All Seasons]," IEEE Solid-State Circuits Magazine, Volume. 8, Issue. 20, pp. 10-15, Spring 2016. [http://www.seas.ucla.edu/brweb/papers/Journals/BRSpring16DeltaSigma.pdf]

P. M. Aziz, H. V. Sorensen and J. vn der Spiegel, "An overview of sigma-delta converters," in IEEE Signal Processing Magazine, vol. 13, no. 1, pp. 61-84, Jan. 1996 [https://sci-hub.st/10.1109/79.482138]

Richard E. Schreier, ECE 1371 Advanced Analog Circuits - 2015 [http://individual.utoronto.ca/schreier/ece1371-2015.html]

Gabor C. Temes. ECE 627-Oversampled Delta-Sigma Data Converters [https://classes.engr.oregonstate.edu/eecs/spring2017/ece627/lecturenotes.html]

Joshua Reiss. Understanding sigma delta modulation: the solved and unsolved issues

[https://www.eecs.qmul.ac.uk/~josh/documents/2008/Reiss-JAES-UnderstandingSigmaDeltaModulation-SolvedandUnsolvedIssues.pdf]

V. Medina, P. Rombouts and L. Hernandez-Corporales, "A Different View of Sigma-Delta Modulators Under the Lens of Pulse Frequency Modulation [Feature]," in IEEE Circuits and Systems Magazine, vol. 24, no. 2, pp. 80-97, Secondquarter 2024