KNOW-HOW

White noise

David Murray. Topic 6: Random Processes and Signals [slides notes]

Mathuranathan. White Noise : Simulation and Analysis using Matlab [https://www.gaussianwaves.com/2013/11/simulation-and-analysis-of-white-noise-in-matlab/]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

clear all; clc; close all;
L=2^20; %Sample length for the random signal
mu=0;
sigma=2;
X=sigma*randn(L,1)+mu;

figure();
subplot(5,1,1)
plot(X);
title(['White noise : \mu_x=',num2str(mu),' \sigma^2=',num2str(sigma^2)])
xlabel('Samples')
ylabel('Sample Values')
grid on

subplot(5,1,2)
n=100; %number of Histrogram bins
[f,x]=hist(X,n);
bar(x,f/trapz(x,f)); hold on;
%Theoretical PDF of Gaussian Random Variable
g=(1/(sqrt(2*pi)*sigma))*exp(-((x-mu).^2)/(2*sigma^2));
plot(x,g, LineWidth=3);hold off; grid on;
title('Theoretical PDF and Simulated Histogram of White Gaussian Noise');
legend('Histogram','Theoretical PDF');
xlabel('Bins');
ylabel('PDF f_x(x)');


subplot(5,1,3)
Rxx=1/L*conv(flipud(X),X);
lags=(-L+1):1:(L-1);

%Alternative method
%[Rxx,lags] =xcorr(X,'biased');
%The argument 'biased' is used for proper scaling by 1/L
%Normalize auto-correlation with sample length for proper scaling

plot(lags,Rxx, LineWidth=4);
title('Auto-correlation Function of white noise');
xlabel('Lags')
ylabel('Correlation')
grid on; hold on;

ss = X.^2;
ssm = sum(ss)/L; % 4.0
stem([0], [ssm], '--o', LineWidth=2)


subplot(5,1,4)
[pxx_norm, f] = pwelch(X, 1024,[],[],1, 'centered');
plot(f, 10*log10(pxx_norm))
axis([-0.5 0.5 0 10]); grid on;
ylabel('PSD (dB/Hz)');
xlabel('Normalized Frequency');
title('Power spectral density of white noise with inbuilt pwelch');

subplot(5,1,5)
%Verifying the constant PSD of White Gaussian Noise Process
%with arbitrary mean and standard deviation sigma

mu=0; %Mean of each realization of Noise Process
sigma=2; %Sigma of each realization of Noise Process

L = 1000; %Number of Random Signal realizations to average
N = 1024; %Sample length for each realization set as power of 2 for FFT

%Generating the Random Process - White Gaussian Noise process
MU=mu*ones(1,N); %Vector of mean for all realizations
Cxx=(sigma^2)*diag(ones(N,1)); %Covariance Matrix for the Random Process
R = chol(Cxx); %Cholesky of Covariance Matrix
%Generating a Multivariate Gaussian Distribution with given mean vector and
%Covariance Matrix Cxx
z = repmat(MU,L,1) + randn(L,N)*R;
%By default, FFT is done across each column - Normal command fft(z)
%Finding the FFT of the Multivariate Distribution across each row
%Command - fft(z,[],2)
Z = 1/sqrt(N)*fft(z,[],2);  % Scaling by sqrt(N);
Pzavg = mean(Z.*conj(Z));   % Computing the **mean power** from fft

normFreq= [-N/2:N/2-1]/N;
Pzavg=fftshift(Pzavg); %Shift zero-frequency component to center of spectrum
plot(normFreq,10*log10(Pzavg),'r');
axis([-0.5 0.5 0 10]); grid on;
ylabel('PSD (dB/Hz)');
xlabel('Normalized Frequency');
title('Power spectral density of white noise');

Julius Orion Smith III. Why an Impulse is Not White [https://www.dsprelated.com/freebooks/sasp/Why_Impulse_Not_White.html]

I.I.D. Noise

Independent and Identically Distributed

Kevin Zheng. The Frequency Domain Trap – Beware of Your AC Analysis [https://circuit-artists.com/the-frequency-domain-trap-beware-of-your-ac-analysis/]

Mathuranathan. White Noise : Simulation and Analysis using Matlab [https://www.gaussianwaves.com/2013/11/simulation-and-analysis-of-white-noise-in-matlab/]

white noise doesn't mean it has a Gaussian/normal distribution

The only criteria for a (discrete) signal to be "white" is for each sample to be independently taken from the same probability distribution

By understanding input signal's statistical nature, we can gather more insights about certain requirements for our circuits than just from frequency domain

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

fs = 1;
N = 2^20;
Nhist = 100;
segmentLength = 512;

x_norm = randn(1, N,1); % Generate random data (e.g., Gaussian white noise)
[pxx_norm, f] = pwelch(x_norm, segmentLength, [], [], fs);

x_uniform = 2*rand(N,1) - 1; % uniform random -1 ~ 1;
[pxx_uniform, ~] = pwelch(x_uniform, segmentLength, [], [], fs);

x_sin = sin(2*pi*(rand(N,1) - 0.5)); % sinusoidal-like
[pxx_sin, ~] = pwelch(x_sin, segmentLength, [], [], fs);

x_bin = 2*randi(2,N,1) -3; % binomial distribution, -1, 1
[pxx_bin, ~] = pwelch(x_bin, segmentLength, [], [], fs);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

val = randn(1, 2^20,1);
val_abs = abs(val);
val_abs_avg = mean(val_abs);
subplot(2,2,1)
histogram(val);
title('x_{norm} distribution'); grid on

subplot(2,2,2)
histogram(val_abs);
title('|x_{norm}| distribution')

subplot(2,2,[3 4])
[pxx, f] = pwelch(val_abs - val_abs_avg, 512, [], [], 1);
plot(f, 10*log10(pxx), LineWidth=4); grid on
title('psd (dB)')

Additive White Gaussian Noise (AWGN)

Qasim Chaudhari. Additive White Gaussian Noise (AWGN) [https://wirelesspi.com/additive-white-gaussian-noise-awgn/]

Mathuranathan. Simulate additive white Gaussian noise (AWGN) channel [https://www.gaussianwaves.com/2015/06/how-to-generate-awgn-noise-in-matlaboctave-without-using-in-built-awgn-function/]

Does PSD (dBm/Hz) of white noise depend on sampling rate?. Does PSD (dBm/Hz) of white noise depend on sampling rate? [https://dsp.stackexchange.com/a/87654/59253]

Matthew Schubert. Colouring Noise - Generating coloured noise to simulate physical processes [https://blog.ioces.com/matt/posts/colouring-noise/]

\[ \text{PSD}_s = \frac{\sigma^2}{f_s} \space\space \text{for two-sided PSD} \space\space\space \text{or}\space\space\space =\frac{\sigma^2}{f_s/2}\space\space \text{for one-sided PSD} \]

that total power will always be the same for any sampling rate used (as long as the histogram of those samples is still \(\sigma_x\)). Thus the power spectral density will be \(\sigma_x^2/f_s\).

How to generate white noise signal from a given PSD? [https://www.mathworks.com/matlabcentral/answers/1968-how-to-generate-white-noise-signal-from-a-given-psd#answer_1498849]

White noise in continuous-time blocks

MathWorks Support Team. [https://www.mathworks.com/matlabcentral/answers/100763-why-have-a-band-limited-white-noise-generator-block-instead-of-just-a-white-noise-generator-block#answer_110112]

Transient Noise and VerilogA Modeling

Integrated Analog Systems D - Lecture 15S CAD (Transient Noise and VerilogA Modeling) [https://youtu.be/YW2nnI3DD_c]

fs=2*noisefmax guarantee zero aliasing within FFT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

`include "disciplines.vams"
`include "constants.vams"

module noise_src(p, n);
    inout p, n;
    electrical p, n;

    parameter real nd = 4e-9 from (0:inf);   // noise density [V/sqrt(Hz)]
    parameter real bw = 1e9   from (0:inf);  // noise bandwidth [Hz]
    parameter integer seed = 271;

    integer iseed;
    real nv;

    analog begin
        @(initial_step) iseed = seed;
        @(timer(0, 0.5/bw)) nv = nd * $rdist_normal(iseed, 0.0, sqrt(bw));
        V(p,n) <+ transition(nv, 0, 0.5/bw);
    end
endmodule

[Gist link]

Colored Noise Generation

Allen B. Downey. Think DSP - Digital Signal Processing in Python [book repo]

Chembian Thambidurai, "Comparison Of Noise Power At Lowpass Filter Output" [link]

—, "On Noise Power At The Bandpass Filter Output" [link]

Steve Smith. An Interesting Fourier Transform - 1/f Noise [https://www.dsprelated.com/showarticle/40.php]

Mathuranathan. Generate correlated Gaussian sequence (colored noise) [https://www.gaussianwaves.com/2019/10/generating-correlated-gaussian-sequences/]

Jeruchim et., al, Simulation of communication systems – modeling, methodology, and techniques, second edition, Kluwer academic publishers, 2002

Two methods to generate colored Gaussian noise for given mean and PSD shape

• Spectral Factorization Method
• Auto-Regressive (AR) Model

Filtering in Time domain

Alessandro Cudazzo. noise generator developed in C99 (white, brown) [https://github.com/alessandrocuda/noise_generator]

Julius Orion Smith III. Spectral Audio Signal Processing [https://www.dsprelated.com/freebooks/sasp/Filtered_White_Noise.html]

with Derivatives approximation, \(H_p(s) = \frac{1}{s\tau + 1} \to H_p(z)=\frac{\alpha}{1 +(\alpha -1)z^{-1}}\), where \(\alpha = \frac{T}{\tau+T}\)

1
2
3
4
5

get_bnoise(){
    RawData = (randq64_double()*2.0 -1.0)/VOLUME_BN;
	SmoothData = SmoothData - (LPF_Beta * (SmoothData - RawData)); // RC Filter
    return SmoothData;
}

Viswanathan, M. (2020). Simulation of Digital Communication Systems Using Matlab (2nd ed.). GaussianWaves

[Github gist]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

%Generation of colored noise in Matlab
a=0.9; %low pass filter parameter

Fs=1000; %sampling rate
Fc=10; % carrier frequency for the dummy signal
recordDuration=120; % seconds; a longer record reduces PSD estimation variance
numSamples=round(recordDuration*Fs);
t=(0:numSamples-1)/Fs; %time base
variance = 1; %variance of white noise

% Generate Gaussian White Noise with zero mean and unit variance
whiteNoise=sqrt(variance)*randn(1,length(t));

% Welch PSD estimate: 50%-overlapped Hann windows average about 116
% segments for this record, reducing the variation of a raw periodogram.
welchSegmentLength = 2048;
welchOverlap = welchSegmentLength/2;
NFFT = 4096;
welchWindow = hann(welchSegmentLength,'periodic');
[whiteNoiseSpectrum,f] = pwelch(whiteNoise,welchWindow,welchOverlap, ...
    NFFT,Fs,'onesided');

% Analytical one-sided white-noise PSD for comparison. DC and Nyquist are
% not doubled in a one-sided PSD.
whiteNoiseTheory = 2*variance/Fs*ones(size(f));
whiteNoiseTheory([1 end]) = variance/Fs;

%Colored Noise Generation
x=whiteNoise;
%First Order Low pass filter y(n)=a*y(n-1)+(1-a)*x(n)
%Filter Trasfer function Y(Z) = X(Z)*(1-a)/(1-aZ^-1)
[y zf]=filter(1-a,[1 -a],x);
coloredNoise = y;
[coloredNoiseSpectrum,f] = pwelch(coloredNoise,welchWindow,welchOverlap, ...
    NFFT,Fs,'onesided');

% Theoretical colored-noise PSD: S_y(f) = S_x(f)*|H(f)|^2.
filterResponse = (1-a)./(1-a*exp(-1j*2*pi*f/Fs));
coloredNoiseTheory = whiteNoiseTheory.*abs(filterResponse).^2;

The input sequence \(x[n]\) is zero-mean discrete-time white Gaussian noise with variance \(\sigma_x^2\). Its one-sided power spectral density is

\[ S_x^{(1)}(f)= \begin{cases} \dfrac{\sigma_x^2}{F_s}, & f=0 \ \text{or}\ f=\dfrac{F_s}{2}, \\[6pt] \dfrac{2\sigma_x^2}{F_s}, & 0<f<\dfrac{F_s}{2}. \end{cases} \label{eq:white_noise_psd} \]

The colored-noise sequence is generated using the first-order digital low-pass filter

\[ y[n]=a\,y[n-1]+(1-a)x[n], \label{eq:colored_noise_filter} \]

whose transfer function is \[ H(z)=\frac{Y(z)}{X(z)} =\frac{1-a}{1-a z^{-1}}. \label{eq:digital_filter_transfer} \]

1
2

[y zf]=filter(1-a,[1 -a],x);
coloredNoise = y;

Evaluating the transfer function on the unit circle gives \[ H\!\left(e^{j2\pi f/F_s}\right) = \frac{1-a} {1-ae^{-j2\pi f/F_s}}, \]

and therefore

\[ \left|H\!\left(e^{j2\pi f/F_s}\right)\right|^2 = \frac{(1-a)^2} {1+a^2-2a\cos\!\left(2\pi f/F_s\right)}. \label{eq:digital_filter_magnitude} \]

Consequently, the theoretical one-sided colored-noise PSD is \[ S_y^{(1)}(f) = S_x^{(1)}(f) \frac{(1-a)^2} {1+a^2-2a\cos\!\left(2\pi f/F_s\right)}. \label{eq:colored_noise_psd} \]

specifically, it is the backward-Euler approximation of a continuous first-order low-pass filter: \[ \tau\frac{dy}{dt}+y=x,\qquad \frac{dy}{dt}\approx F_s(y[n]-y[n-1]) \] This produces: \[ y[n]=a\,y[n-1]+(1-a)x[n],\qquad a=\frac{\tau F_s}{1+\tau F_s} \] Therefore the corresponding continuous-time cutoff is: \[ \boxed{\omega_c=\frac{1-a}{a}F_s\ \text{rad/s}} \]

However, this is not the exact −3 dB frequency of the resulting digital filter. Its exact digital cutoff is: \[ \boxed{\omega_{3\text{dB,digital}} =F_s\cos^{-1}\!\left(1-\frac{(1-a)^2}{2a}\right)\ \text{rad/s}} \]

For a = 0.9 and Fs = 1000:

• Backward-Euler continuous cutoff: 111.11 rad/s (17.68 Hz)
• Exact digital −3 dB cutoff: 105.46 rad/s (16.78 Hz)

Now we derive \(\omega_{3\text{dB,digital}}\), Start with the digital transfer function: \(H(z)=\frac{1-a}{1-az^{-1}}\)

Evaluate it on the unit circle, \(z=e^{j\Omega}\), where \(Omega\) is digital frequency in rad/sample: \(H(e^{j\Omega})=\frac{1-a}{1-ae^{-j\Omega}}\)

Its magnitude squared is \(|H(e^{j\Omega})|^2 =\frac{(1-a)^2}{|1-ae^{-j\Omega}|^2}\)

Expanding the denominator: \[ \begin{aligned} |1-ae^{-j\Omega}|^2 &=(1-a\cos\Omega)^2+(a\sin\Omega)^2\\ &=1+a^2-2a\cos\Omega\\ &=(1-a)^2+2a(1-\cos\Omega). \end{aligned} \]

The DC gain is one: \(|H(e^{j0})|^2=1\)

At the −3 dB frequency, power is half its DC value: \(|H(e^{j\Omega_{3\mathrm{dB}}})|^2=\frac{1}{2}\)

Therefore, \(\frac{(1-a)^2} {(1-a)^2+2a(1-\cos\Omega_{3\mathrm{dB}})} =\frac12\)

and hence \[ \boxed{ \Omega_{3\mathrm{dB}} =\cos^{-1}\!\left(1-\frac{(1-a)^2}{2a}\right) } \quad\text{rad/sample} \] Since (=F_s), \[ \boxed{ \omega_{3\mathrm{dB}} =F_s\cos^{-1}\!\left(1-\frac{(1-a)^2}{2a}\right) } \quad\text{rad/s} \]

For (a=0.9) and (F_s=1000):

\(\Omega_{3\mathrm{dB}}\approx0.10546\ \text{rad/sample}\), \(\omega_{3\mathrm{dB}}\approx105.46\ \text{rad/s} \approx16.78\ \text{Hz}\)

Filtering in Frequency domain

Matthew Schubert. Colouring Noise - Generating coloured noise to simulate physical processes [https://blog.ioces.com/matt/posts/colouring-noise/] [https://gist.github.com/m-schubert/45c562146c6607b8990f1e8f34ff87b0]

White, Pink \(1/f\), Brownian \(1/f^2\), Blue \(f\), Violet \(f^2\)

The process of generating coloured noise is relatively simple:

1. Start with a representation of white noise signal in the frequency domain
2. Shape the signal in the frequency domain according to the PSD you'd like to achieve
3. Take the inverse Fourier transform of the shaped signal

Sampling shaping transfer function (not scaled by \(1/T_s\)) make sense in time domain convolution between sampled noise and sampled impulse response of filter

AR(N) Model Method

Generate color noise using Auto-Regressive (AR) model [https://www.gaussianwaves.com/2019/12/color-noise-generation-using-auto-regressive-ar-model-power-law-noises/]

Konstantinos Chatzilygeroudis. Lecture 9 & 10: Noise Models & Linear Filters [notes, slides]

Autoregressive (AR) modeling in signal processing represents a signal as a linear combination of its own previous values plus a white noise error term, effectively acting as an all-pole IIR filter

Google AI Mode [https://share.google/aimode/QAuvWdwJFng54cYZo]

1
2
3
4
5
6
7
8
9
10
11
12
13

% https://github.com/vineel49/colored_noise/blob/master/RUN_ME.m


% IIR FILTER PARAMETERS (USED TO GENERATE COLOURED NOISE)
a = 0.99;
B = sqrt(1-a^2); % INPUT COEFFICIENTS IN THE DIFFERENCE EQUATION
A = [1 -a]; % OUTPUT COEFFICIENTS IN THE DIFFERENCE EQUATION

% ADDITIVE COLOURED GAUSSIAN NOISE
% AWGN
AWGN = normrnd(0,NOISE_STD_DEV,1,1000+FRAME_SIZE)+1i*normrnd(0,NOISE_STD_DEV,1,1000+FRAME_SIZE);
ACGN = filter(B,A,AWGN);
ACGN(1:1000) = []; % DISCARDING TRANSIENT SAMPLES

impulse sampling noise

Chembian Thambidurai, "Noise, Sampling and Zeta Functions" [link]

A random signal \(v_n(t)\) is sampled using an ideal impulse sampler

Sampling coloured noise

converging PSD

integrated power of the sampled signal in the Nyquist band

sampling bandlimited white noise

Kundert, Ken. (2006). Simulating Switched-Capacitor Filters with SpectreRF [https://designers-guide.org/analysis/sc-filters.pdf]

Pavan, Schreier and Temes, "Understanding Delta-Sigma Data Converters, Second Edition" ISBN 978-1-119-25827-8

Tania Khanna, ESE568 Fall 2019, Mixed Signal Circuit Design and Modeling URL: https://www.seas.upenn.edu/~ese568/fall2019/

Matt Pharr, Wenzel Jakob, and Greg Humphreys. 2016. Physically Based Rendering: From Theory to Implementation (3rd. ed.). Morgan Kaufmann Publishers Inc., San Francisco, CA, USA.

R. Gregorian and G. C. Temes. Analog MOS Integrated Circuits for Signal Processing. Wiley-Interscience, 1986

Trevor Caldwell, Lecture 9 Noise in Switched-Capacitor Circuits [http://individual.utoronto.ca/trevorcaldwell/course/NoiseSC.pdf]

Christian-Charles Enz. High precision CMOS micropower amplifiers [pdf]

The aliasing of the noise, or noise folding, plays an important role in switched-capacitor as it does in all switched-capacitor filters

Assume for the moment that the switch is always closed (that there is no hold phase), the single-sided noise density would be

\(v_s[n]\) is the sampled version of \(v_{RC}(t)\), i.e. \(v_s[n]= v_{RC}(nT_C)\) \[ S_s(e^{j\omega}) = \frac{1}{T_C} \sum_{k=-\infty}^{\infty}S_{RC}(j(\frac{\omega}{T_C}-\frac{2\pi k}{T_C})) \cdot \mathrm{d}\omega \] where \(\omega \in [-\pi, \pi]\), furthermore \(\frac{\mathrm{d}\omega}{T_C}= \mathrm{d}\Omega\) \[ S_s(j\Omega) = \sum_{k=-\infty}^{\infty}S_{RC}(j(\Omega-k\Omega_s)) \cdot \mathrm{d}\Omega \]

To implement a zero-order hold involves convolving the sequence \(v_s\) with a pulse of unit height with a width of \((1-m)T_c\) and the highlighting \(T_c\) bridge sequence to impulse

where \(m\) is the duty cycle

\[ \boxed{\color{purple}\overline{v_c^2} = \overline{v_s^2} = \frac{kT}{C}} \]

Below analysis focusing on sampled noise \(v_s\)

Boris Murmann. Noise Analysis in Switched-Capacitor Circuits, ISSCC 2011 / tutorials [slides, transcript]

—. EE315A VLSI Signal Conditioning Circuits [pdf]

—. EE315B VLSI Data Conversion Circuits, Autumn 2013 [pdf]

• Calculate autocorrelation function of noise at the output of the RC filter
• Calculate the spectrum by taking the discrete time Fourier transform of the autocorrelation function

Bernhard E. Boser . Advanced Analog Integrated Circuits Switched Capacitor Gain Stages [https://people.eecs.berkeley.edu/~boser/courses/240B/lectures/M05%20SC%20Gain%20Stages.pdf]

P. Bruschi, Microelectronic System Design, [https://docenti.ing.unipi.it/~a008309/mat_stud/MIXED/2023/Slides_pdf/05_Switches_and_caps.pdf]

Cyclostationary Noise (Modulated Noise)

[https://ece-research.unm.edu/bsanthan/ece541/cyclo.pdf]

Chembian Thambidurai, "Power Spectral Density of Pulsed Noise Signals" [link]

White Noise Modulation

Noisy Resistor & Clocked Switch

\[ v_t (t) = v_i(t)\cdot m_t(t) \]

where \(v_i(t)\) is input white noise, whose autocorrelation is \(A\delta(\tau)\), and \(m_t(t)\) is periodically operating switch, then autocorrelation of \(v_t(t)\) \[ R_t (t_1, t_2) = E[v_t(t_1)\cdot v_t(t_2)] = R_i(t_1, t_2)\cdot m_t(t_1)m_t(t_2) \]

Then \[ R_t(t, t-\tau) = R_i(\tau)\cdot m_t(t)m_t(t-\tau) = A\delta(\tau) \cdot m_t(t)m_t(t-\tau) = A\delta(\tau) \cdot m_t(t) \] Because \(m_t(t)=m_t(t+T)\), \(R_t(t, t-\tau)\) is is periodic in the variable \(t\) with period \(T\)

The time-averaged ACF is denoted as \(\tilde{R_t}(\tau)\)

\[ \tilde{R}_{t}(\tau) = m\cdot A\delta(\tau) \] That is, \[ \boxed{S_t(f) = m\cdot S_{A}(f)} \]

alternative method, inspired by Claude

\[ \boxed{S_O=H^2*S_I=S_I\sum_{m=-\infty}^{\infty}|c_m|^2} \] with CTFS's Parseval's Relation — \(\frac{1}{T} \int_{0}^{T} \vert{}f(x)\vert{}^2 \, dx = \sum_{n=-\infty}^{\infty} \vert{}c_n\vert{}^2\) \[ \sum_{m=-\infty}^{\infty}|c_m|^2 = \mathcal{D}\cdot \mathcal{h}^2 \] where \(\mathcal{D}\) is duty cycle and \(\mathcal{h}\) is height of periodic pulse

Then, Two-sided PSD is \[ \boxed{S_O=S_I\cdot \mathcal{D}\cdot \textcolor{blue}{\mathcal{h}^2}} \]

Colored Noise Modulation

\[ \tilde{R_t}(\tau) = R_i(\tau)\cdot m_{tac}(\tau) \]

where \(m_t(t)m_t(t-\tau)\) averaged on \(t\) is denoted as \(m_{tac}(\tau)\) or \(\overline{m_t(t)m_t(t-\tau)}\)

The DC value of \(m_{tac}(\tau)\) can be calculated as below

1. for \(m\le 0.5\), the DC value of \(m_{tac}(\tau)\) \[ \frac{m\cdot mT}{T} = m^2 \]

2. for \(m\gt 0.5\), the DC value of \(m_{tac}(\tau)\) \[ \frac{(m+2m-1)(1-m)T + (2m-1)\{mT -(1-m)T\}}{T} = m^2 \]

Therefore, time-average power spectral density and total power are scaled by \(m^2\) in fundamental frequency sideband

\[ \boxed{S_t(f) = m^2\cdot S_{A}(f)} \]

Track signal in Switched-Capacitor

\[ \color{blue}\boxed{\text{switch thermal noise is modulated by the clock first, then shaped by the RC low-pass}} \]

track signal pnoise (sc)

zoom in first harmonic by linear step of pnoise

decreasing the rising/falling time of clock, the harmonics still retain

equivalent circuit for pnoise (eq)

1. thermal noise of R is modulated at first
2. then filtered by ideal filter

sc vs eq

• sc: harmonic distortion
• eq: no harmonic distortion

Non-Stationary Processes (Comparator)

T. Sepke, P. Holloway, C. G. Sodini and H. -S. Lee, "Noise Analysis for Comparator-Based Circuits," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 56, no. 3, pp. 541-553, March 2009 [https://dspace.mit.edu/bitstream/handle/1721.1/61660/Speke-2009-Noise%20Analysis%20for%20Comparator-Based%20Circuits.pdf]

—. "Comparator design and analysis for comparator-based switched-capacitor circuits." (2006). [https://dspace.mit.edu/handle/1721.1/38925]

WSS white noise input
white noise step input

Wide-Sense-Stationary Noise

Much like sinusoidal-steady-state signal analysis, steady-state noise analysis methods assume an input \(x(t)\) of infinite duration, which is a Wide-Sense Stationary (WSS) random process

Frequency-domain Analysis

Time-domain Analysis

The output \(y(t)\) of a linear time-invariant (LTI) system \(h(t)\) \[\begin{align} R_{yy}(\tau) &= R_{xx}(\tau)*[h(\tau)*h(-\tau)] \\ &= S_{xx}(0)\delta(\tau) * [h(\tau)*h(-\tau)] \\ &= S_{xx}(0)[h(\tau)*h(-\tau)] \\ &= S_{xx}(0) \int_\alpha h(\alpha)h(\alpha-\tau)d\alpha \end{align}\]

with WSS white noise input \(x(t)\), \(R_{xx}(\tau)=S_{xx}(0)\delta(\tau)\), therefore

\[ V_o(s) = \frac{1}{C}\frac{RC}{1+sRC}\cdot I_n(s) \overset{\mathcal{L}} {\longrightarrow} \frac{1}{C}e^{-t/\tau_0} \]

where \(\tau_0 = RC\)

Non-stationary Noise

Assuming the noise applied duration is much less than the time constant, the output voltage does not reach steady-state and WSS noise analysis does not apply

Time-domain Analysis

The step noise input \(x(t) = \nu(t)u(t)\) where an underlying WSS process \(\nu(t)\) \[ R_{xx}(t_1,t_2) = E[x(t_1)x(t_2)] = R_{\nu\nu}(t_1, t_2)u(t_1)u(t_2)=R_{\nu\nu}(t_1, t_2) \tag{3.28} \]

\[ R_{xy}(t_1, t_2) = E[x(t_1)y(t_2)] = E[x(t_1)(x(t_2)*h(t_2))] = E(x(t_1)x(t_2))*h(t_2) = R_{xx}(t_1,t_2)*h(t_2) \]

\[ R_{yy}(t_1,t_2) = E[y(t_1)y(t_2)] = E[(x(t_1)*h(t_1))y(t_2)] = E[x(t_1)y(t_2)]*h(t_1)=R_{xy}(t_1,t_2)*h(t_1) \]

the absolute value of each time index is important for a non-stationary signal, and only the time difference was important for WSS signals

\[\begin{align} R_{yy}(t_1,t_2) &= h(t_1)*R_{\nu\nu}(t_1, t_2)*h(t_2) \\ &= h(t_1)*S_{xx}(0)\delta(t_2-t_1)*h(t_2) \\ &=S_{xx}(0) h(t_1)*(\delta(t_2-t_1)*h(t_2)) \\ &= S_{xx}(0)h(t_1)*h(t_2-t_1) \\ &= S_{xx}(0)\int_\tau h(\tau)h(t_2-t_1+\tau))d\tau \end{align}\]

That is \[ \sigma^2_y (t)= R_{yy}(t_1,t_2)|_{t_1=t_2=t}=S_{xx}(0)\int_{-\infty}^t |h(\tau)|^2d\tau \tag{3.33} \]

\(t\), the upper limit of integration is just intuitive, which lacks strict derivation

Because stable systems have impulse responses that decay to zero as time goes to infinity, the output noise variance approaches the WSS result as time approaches infinity

Richard Schreier. ECE1371 Advanced Analog Circuits Lecture 8 - COMPARATOR & FLASH ADC DESIGN [http://individual.utoronto.ca/schreier/lectures/2015/8-6.pdf]

\[ R_{yy}(0) = \frac{1}{2\pi}\int_{-\infty}^{\infty}|H(\omega)|^2S_{xx}(\omega)\mathrm{d}\omega = S \cdot \frac{1}{2\pi}\int_{-\infty}^{\infty}|H(\omega)|^2\mathrm{d}\omega \overset{\text{Parseval's Relation}}{=} S\cdot \int_{-\infty}^{\infty}|h(t)|^2\mathrm{d}t \]

Frequency-domain Analysis

Because the definition of the PSD assumes that the variance of the noise process is independent of time, the PSD of a non-stationary process is not very meaningful

Input Referred Noise

Noise Voltage to Timing Jitter Conversion & noise gain

\[\begin{align} \overline{v_n^2}(t_i) &= \frac{\overline{v_{on}^2}}{|A_N|^2} \\ &= \frac{G_n}{G_m}\frac{kT}{C}\frac{1}{A_0}\frac{1+e^{-t_i/\tau_o}}{1-e^{-t_i/\tau_o}} \\ &=4kT\frac{G_n}{G_m^2}\frac{1}{4R_oC} \coth(\frac{t_i}{2\tau_o}) \\ &= 4kTR_n\frac{1}{4\tau_o} \coth(\frac{t_i}{2\tau_o}) \end{align}\]

where \(R_n = \frac{G_n}{G_m^2}\), the equivalent thermal noise resistance

Suppose \(t_i \ll \tau_0\) \[ \overline{v_n^2}(t_i) = 4kTR_n\frac{1}{4\tau_o} \coth(\frac{t_i}{2\tau_o}) \approx 4kTR_n\frac{1}{4\tau_o} \frac{1 + (1-\frac{t_i}{\tau_0})}{1 - (1-\frac{t_i}{\tau_0})} =4kTR_n \cdot \frac{1}{2t_i} \]

Suppose \(t_i \gg \tau_0\) \[ \overline{v_n^2}(t_i) = 4kTR_n\frac{1}{4\tau_o} \coth(\frac{t_i}{2\tau_o}) \approx 4kTR_n\frac{1}{4\tau_o} = \frac{G_n}{G_m}\frac{kT}{C}\frac{1}{A_0} \] As expected, the input referred noise voltage is \(kT/C\) noise

Windowed Integrals of Noise

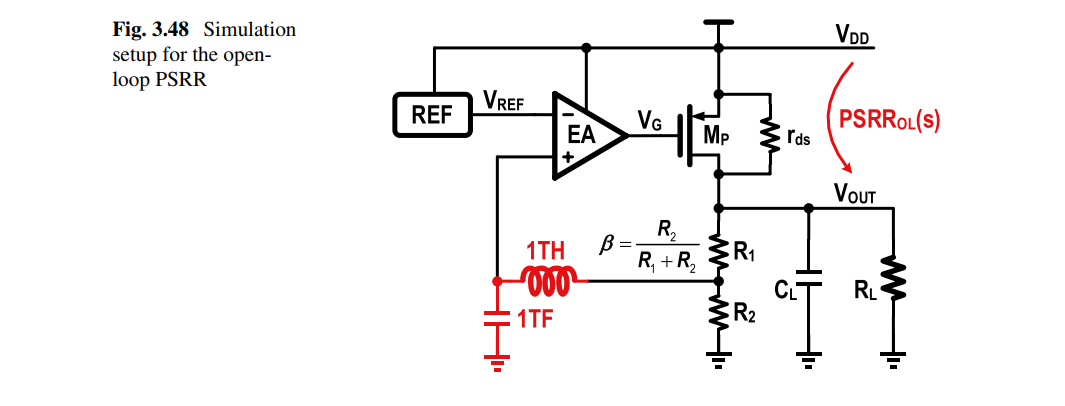
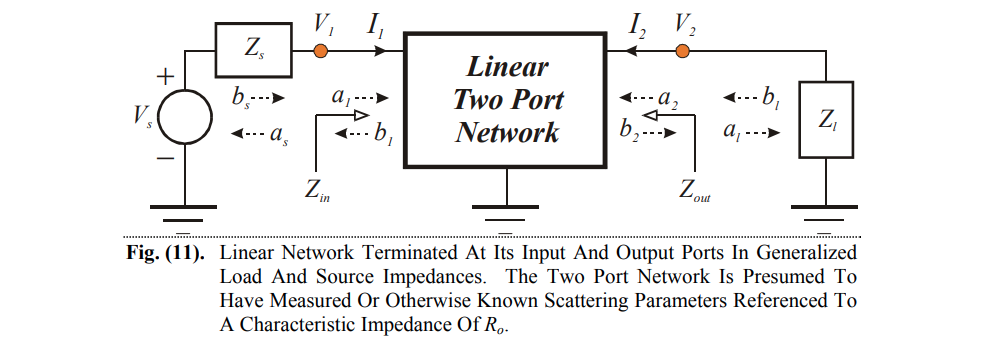
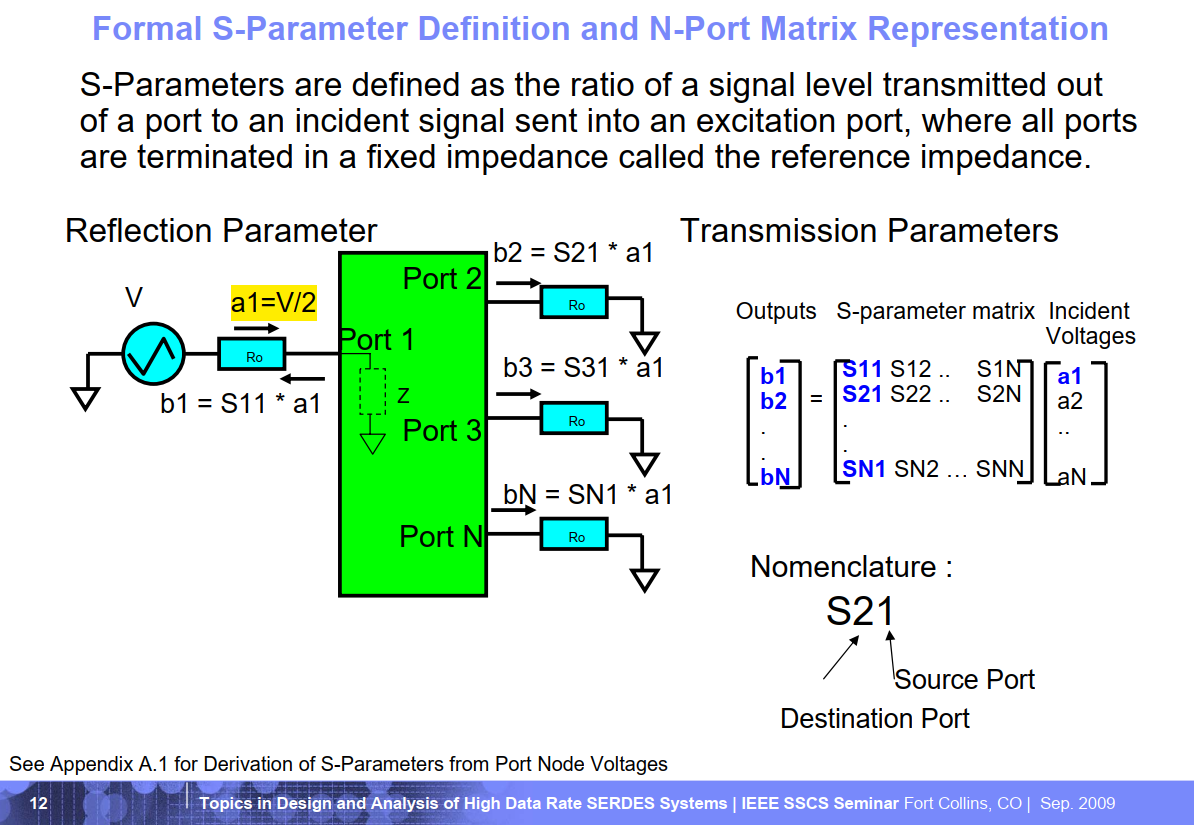
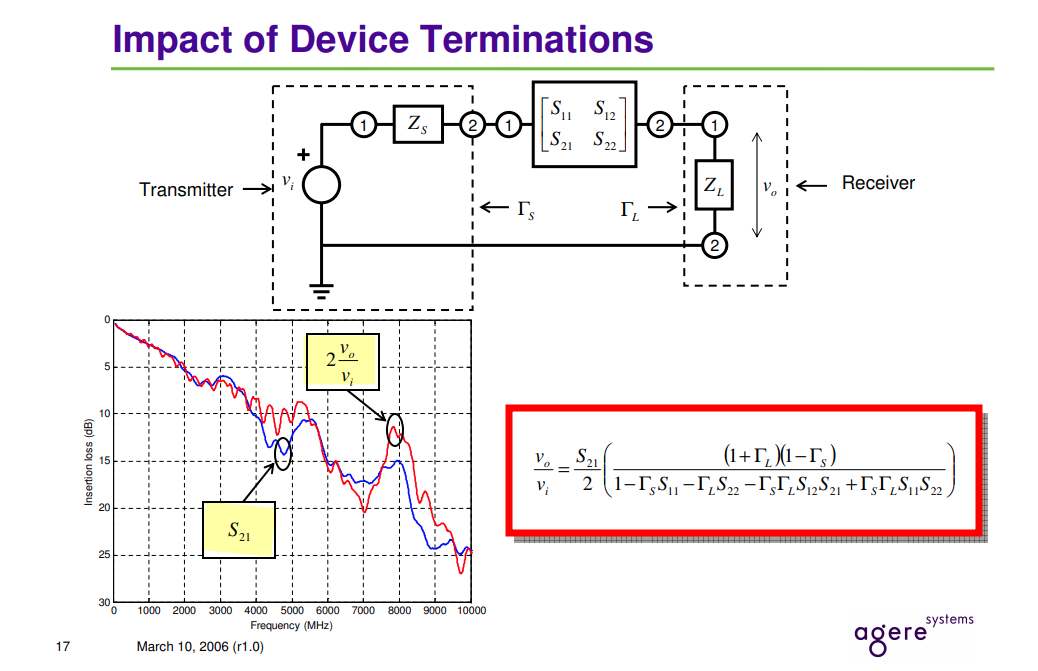
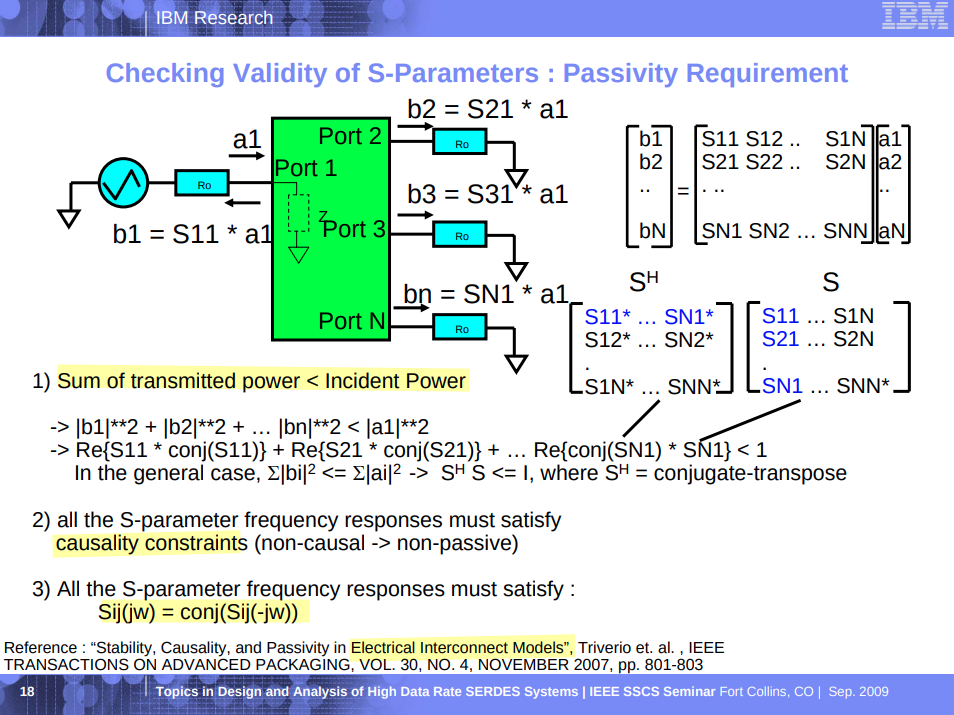
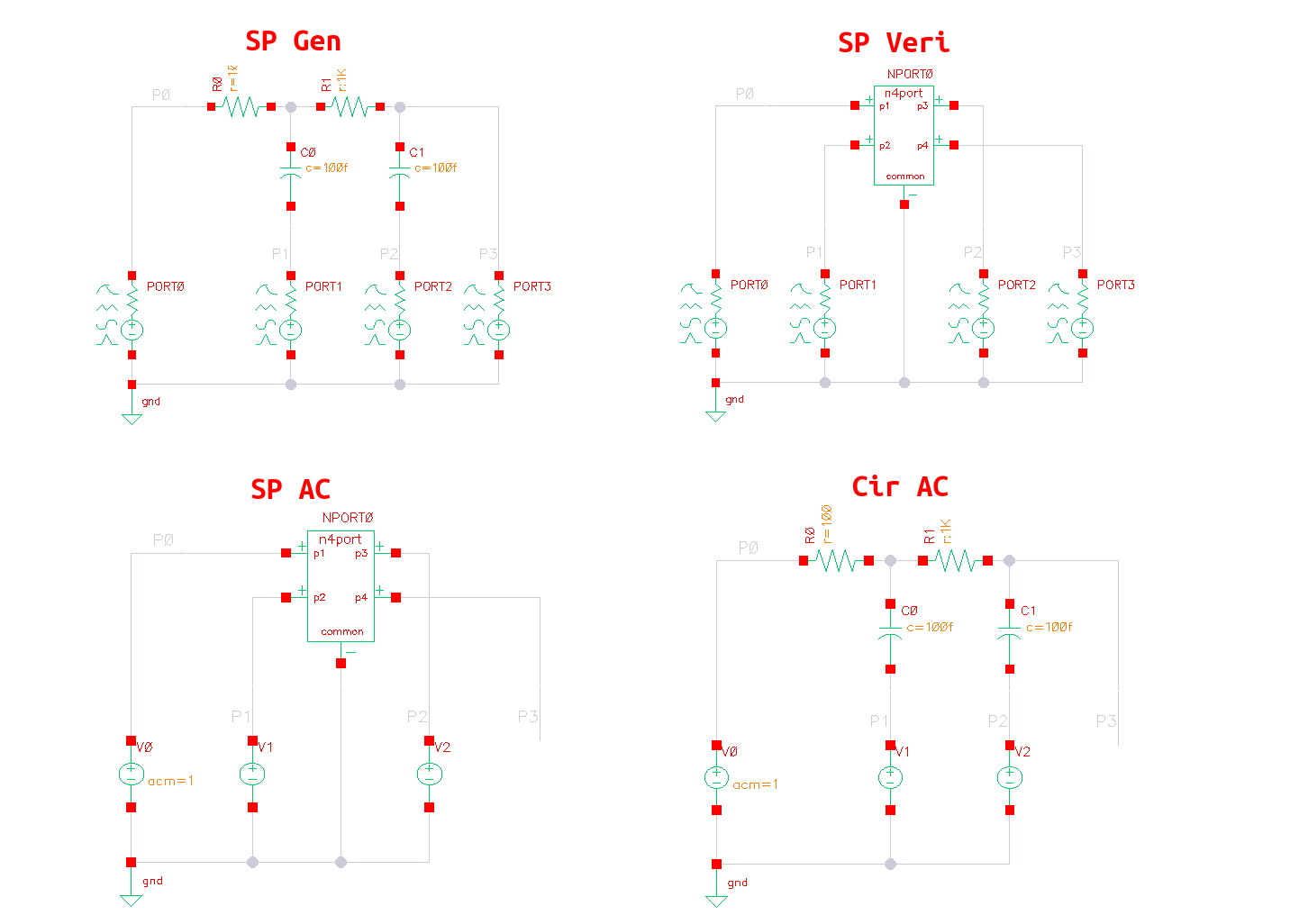
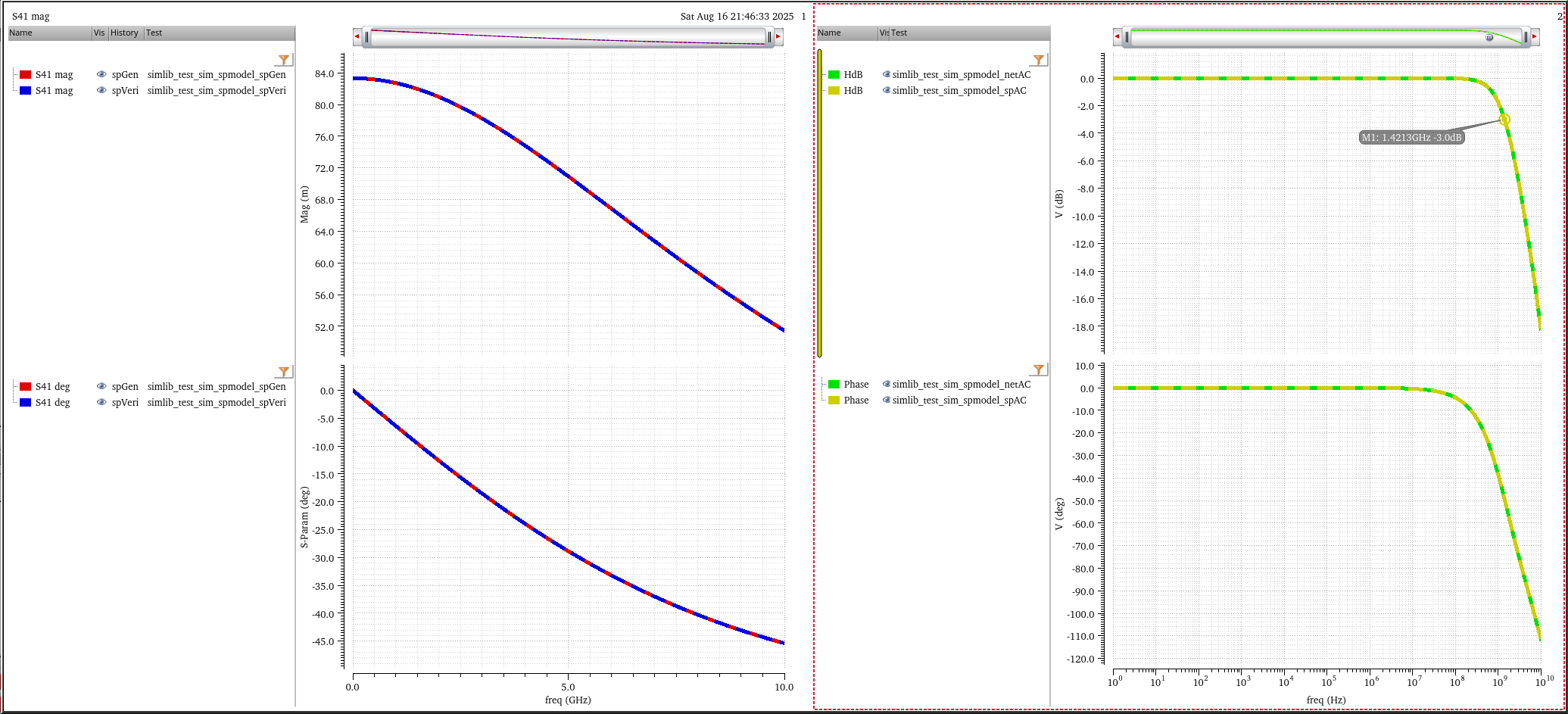
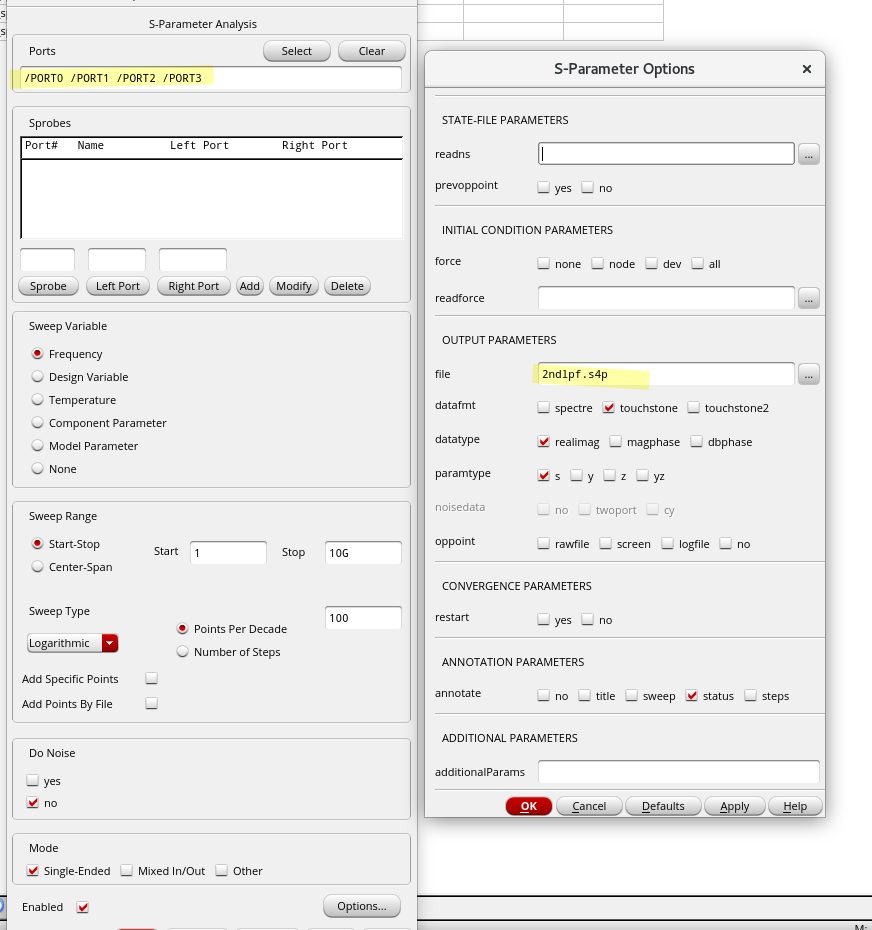
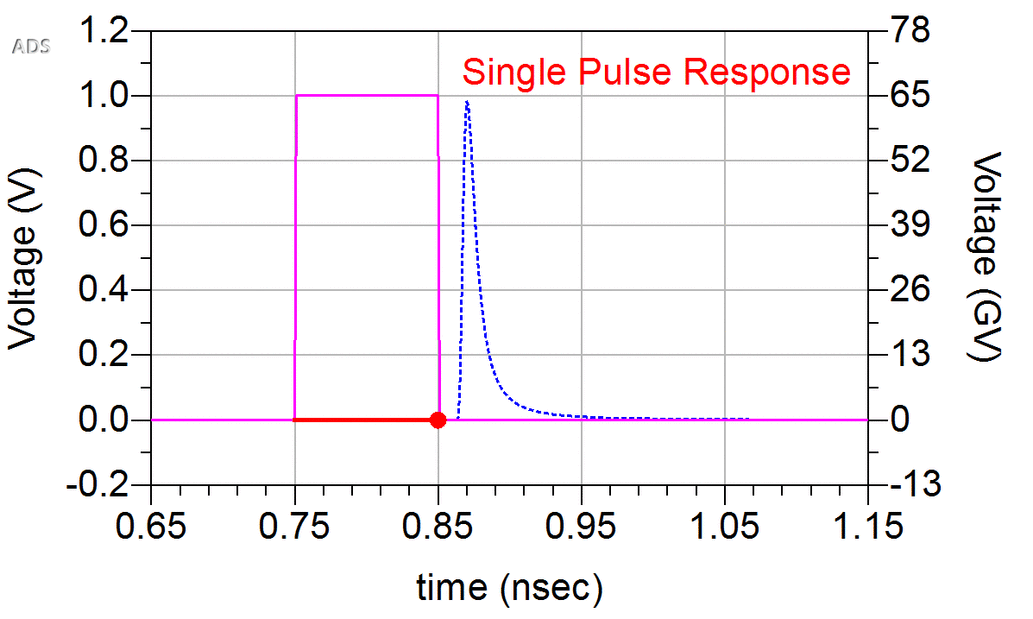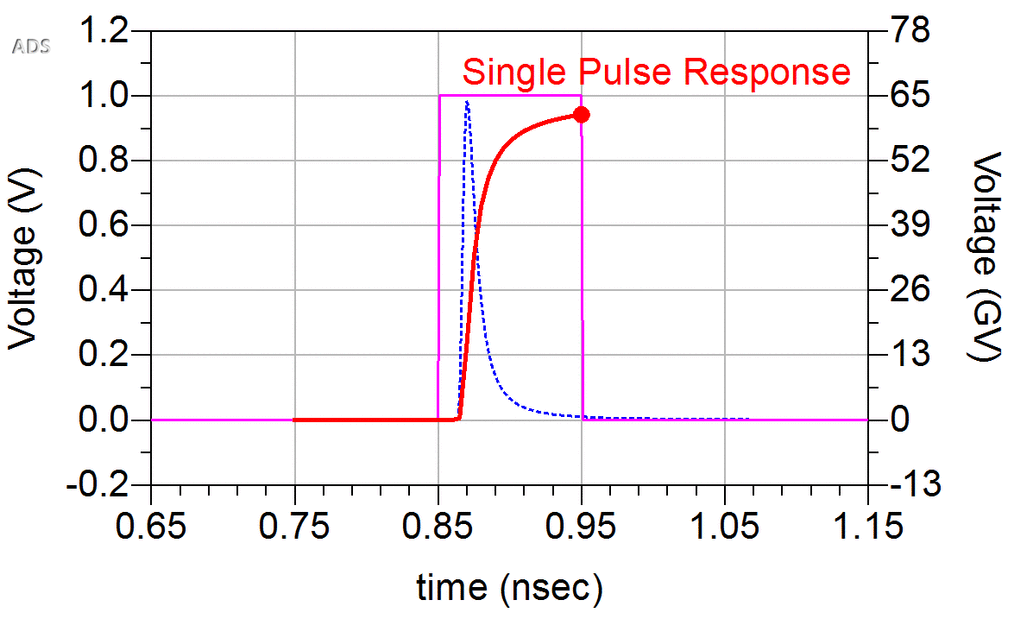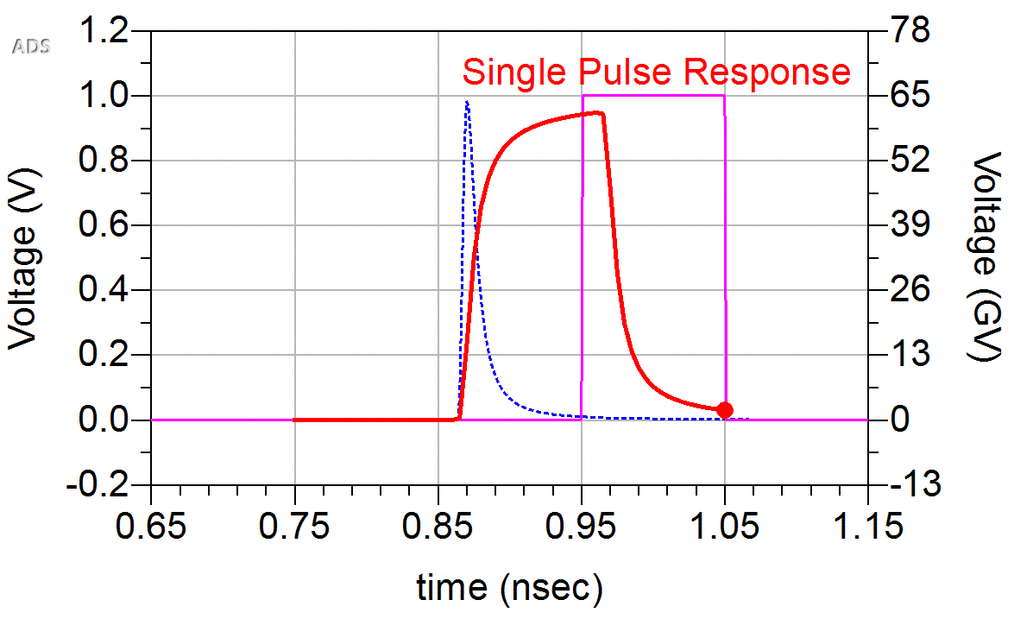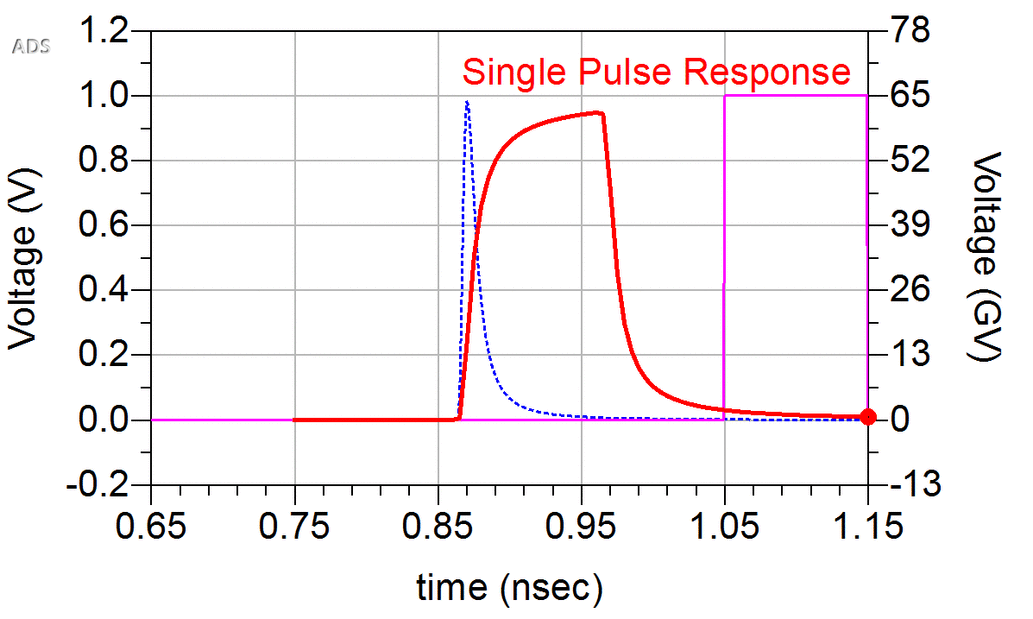
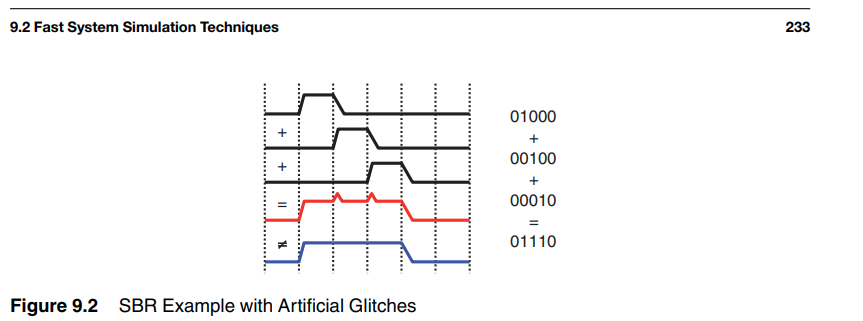
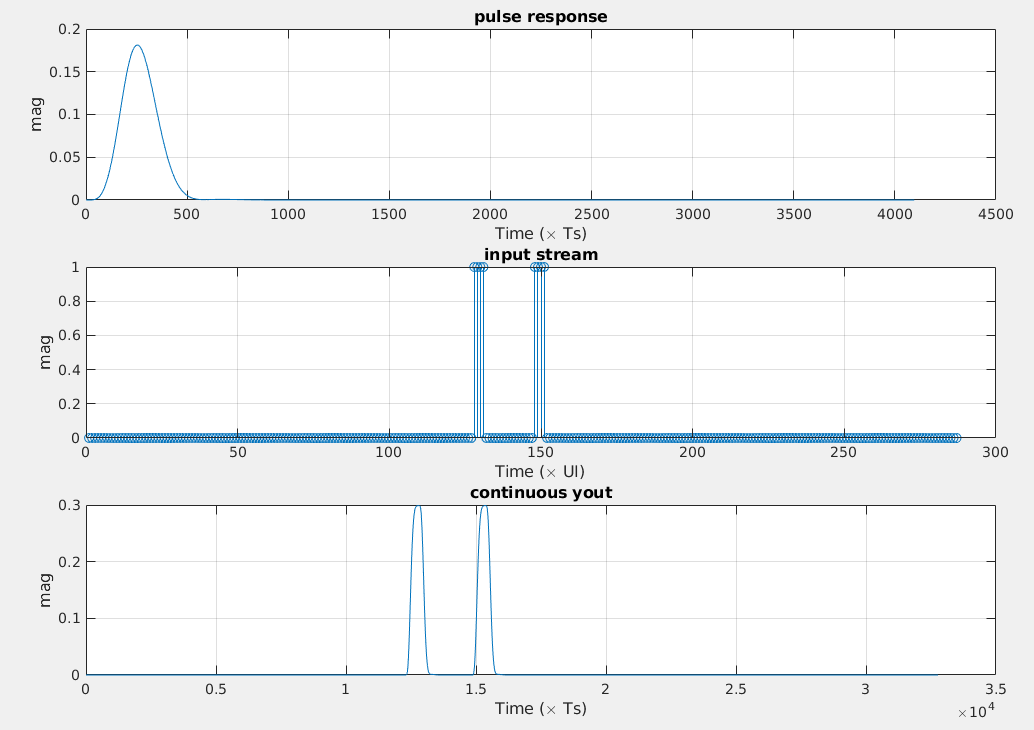
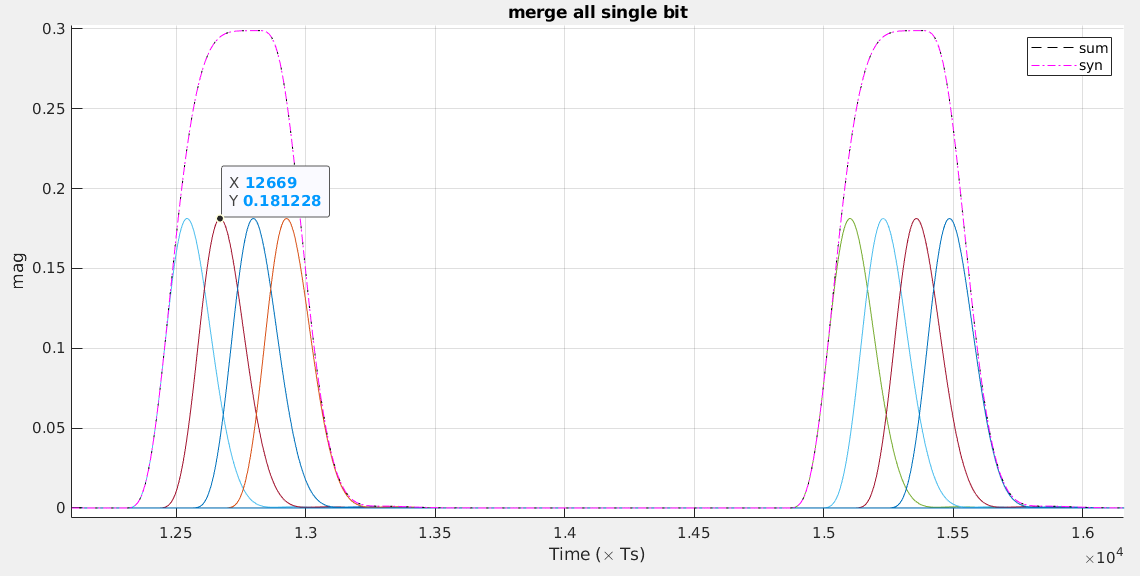
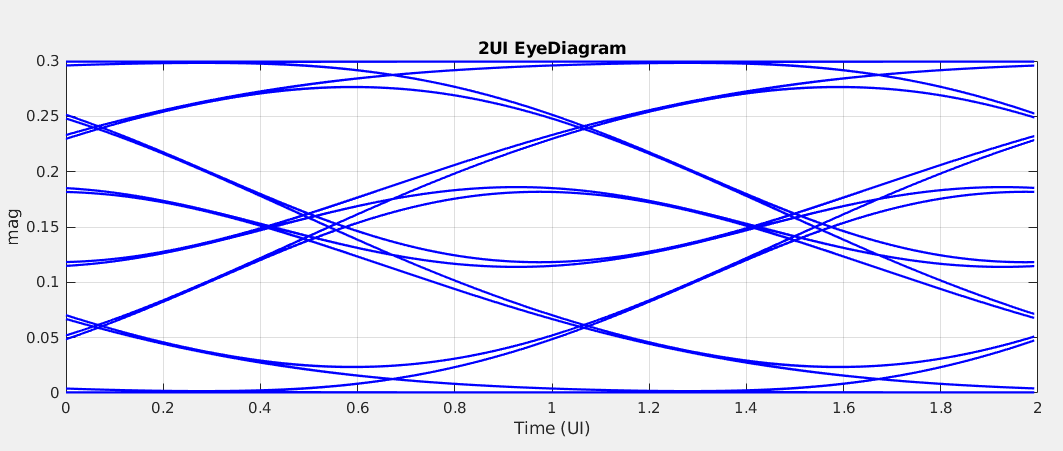
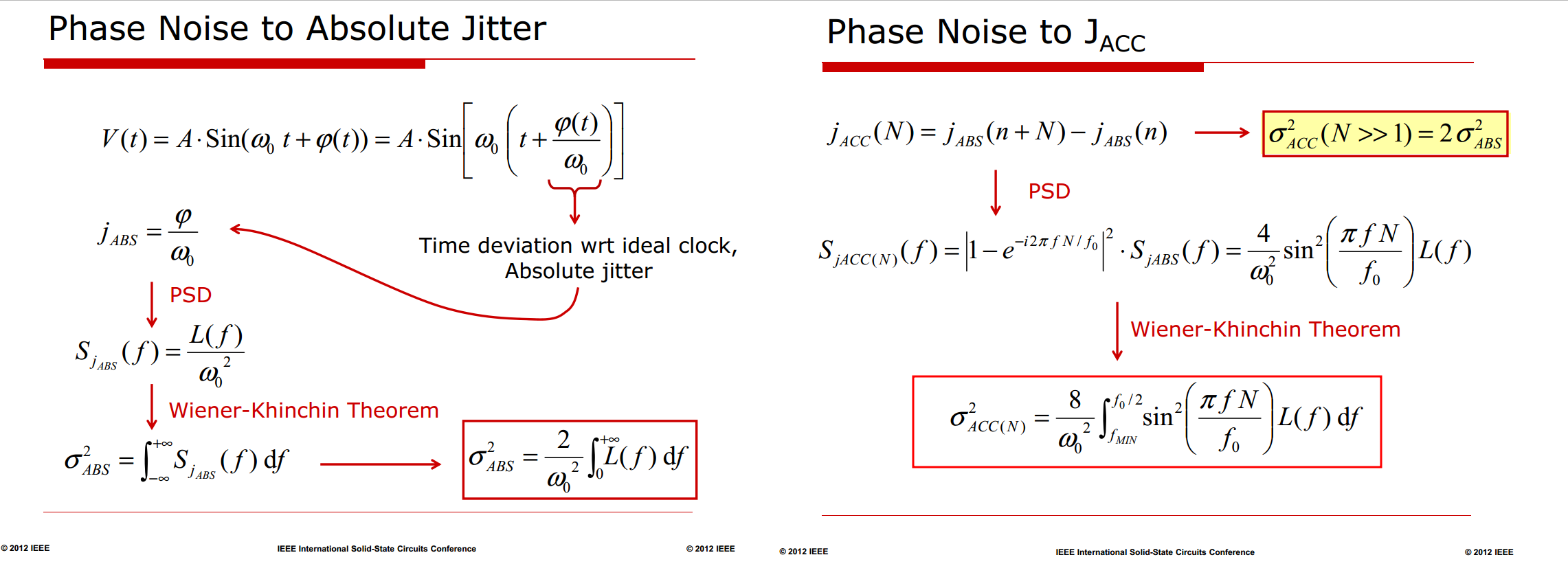
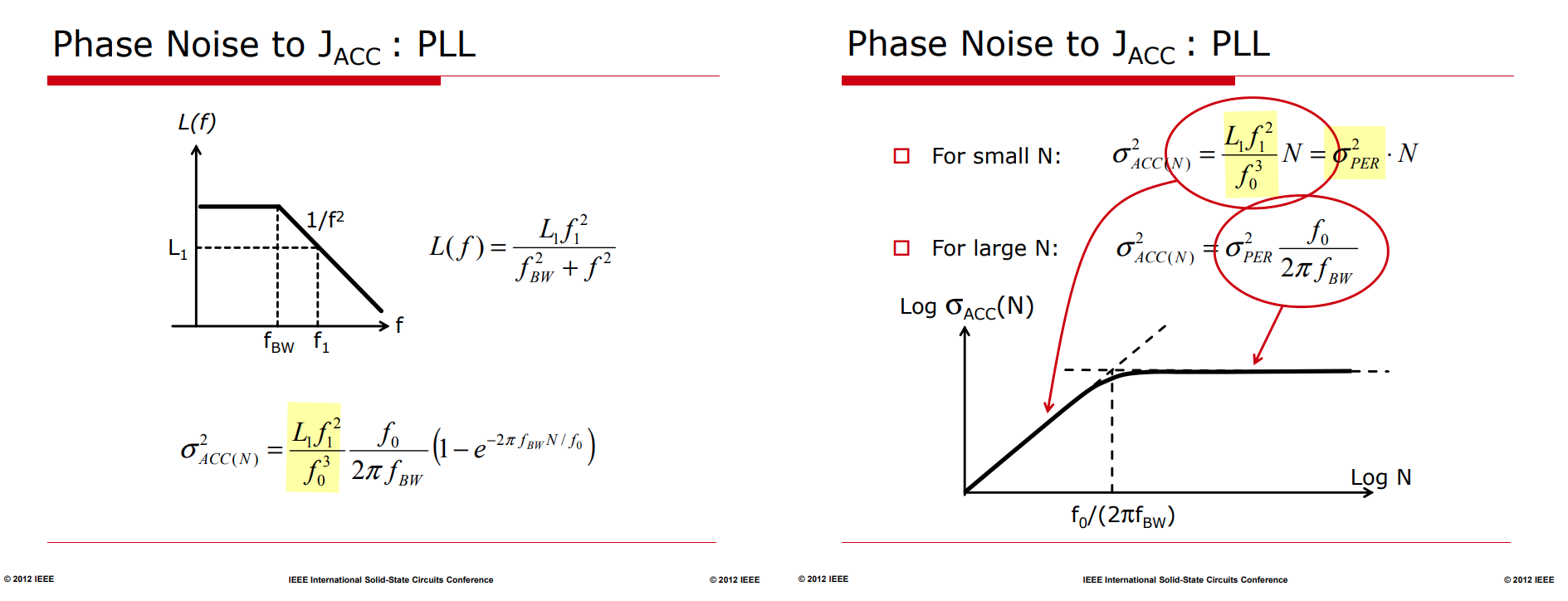
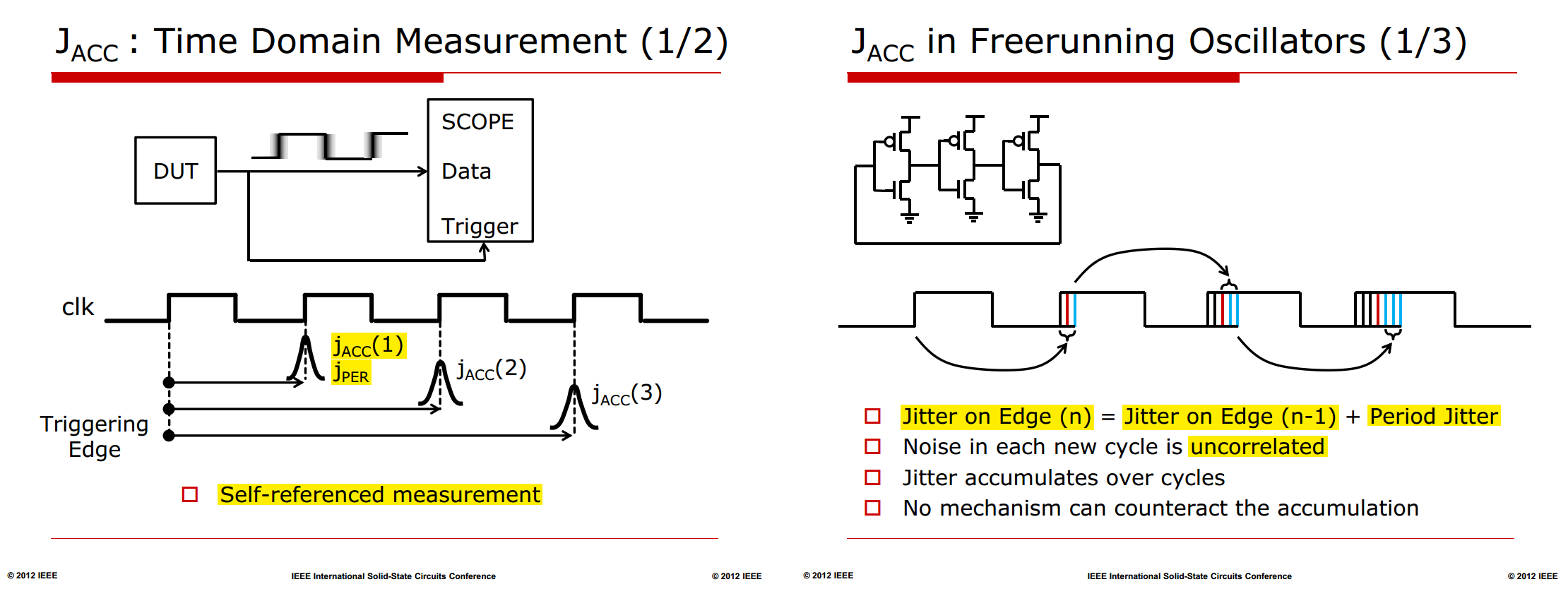
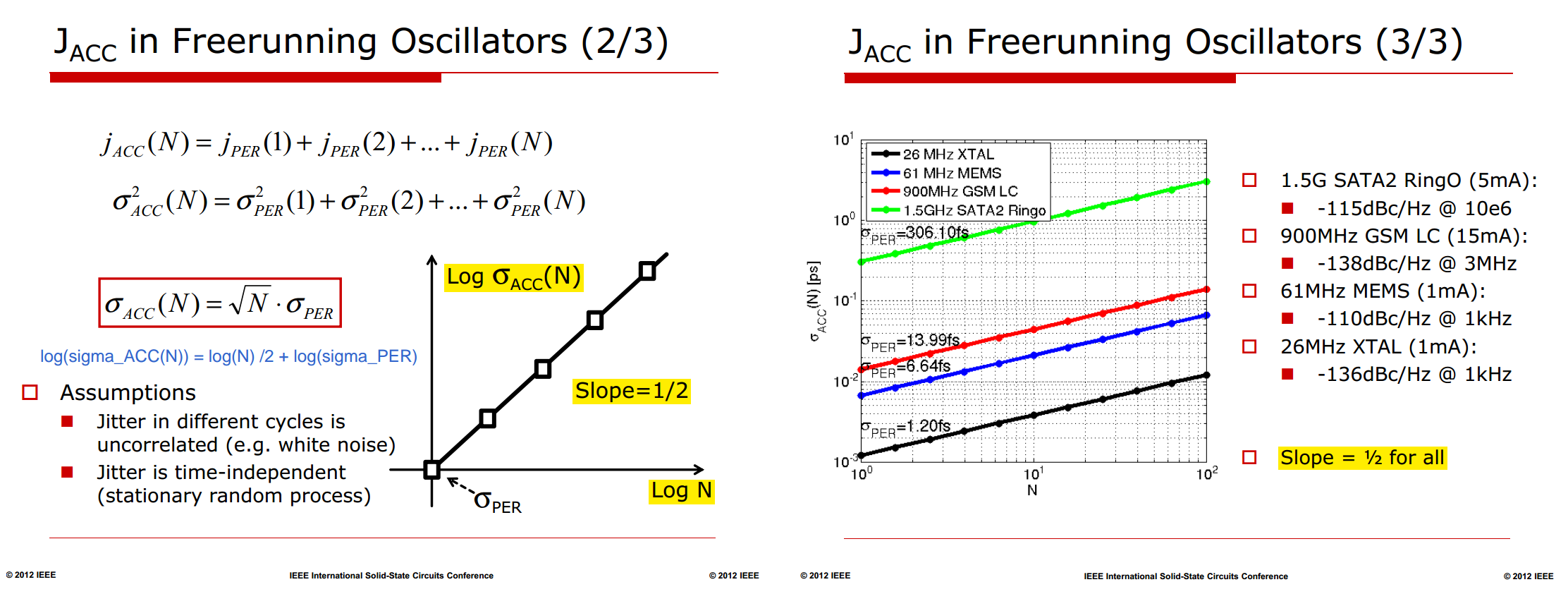
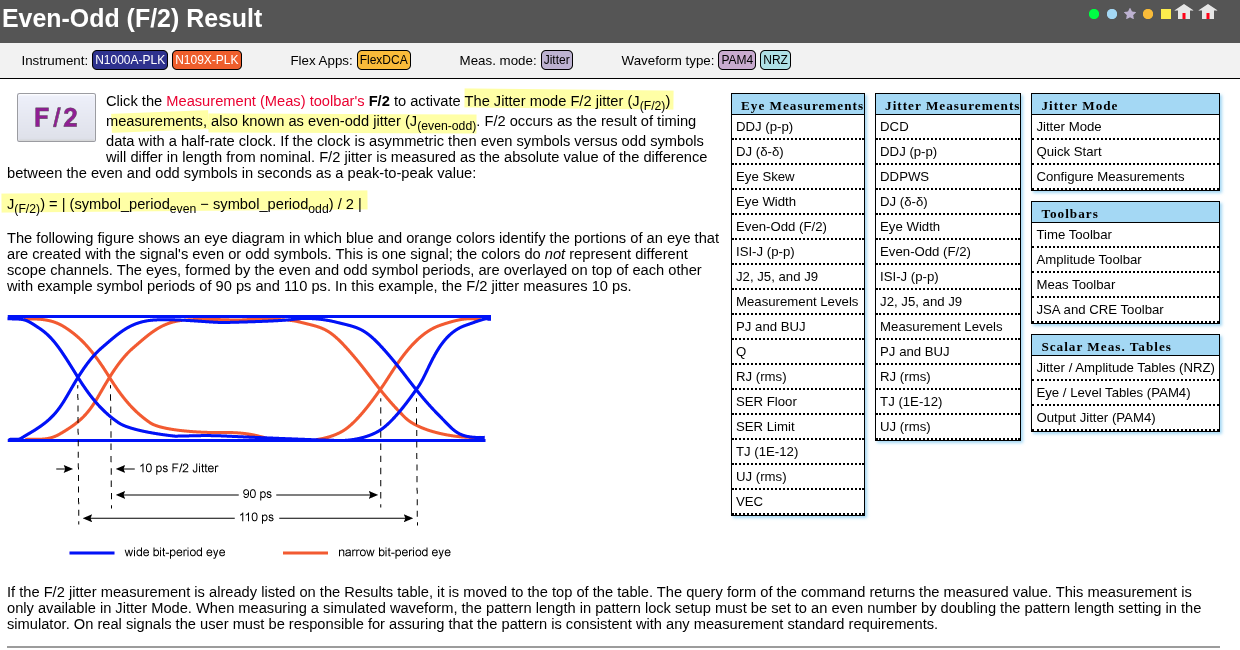
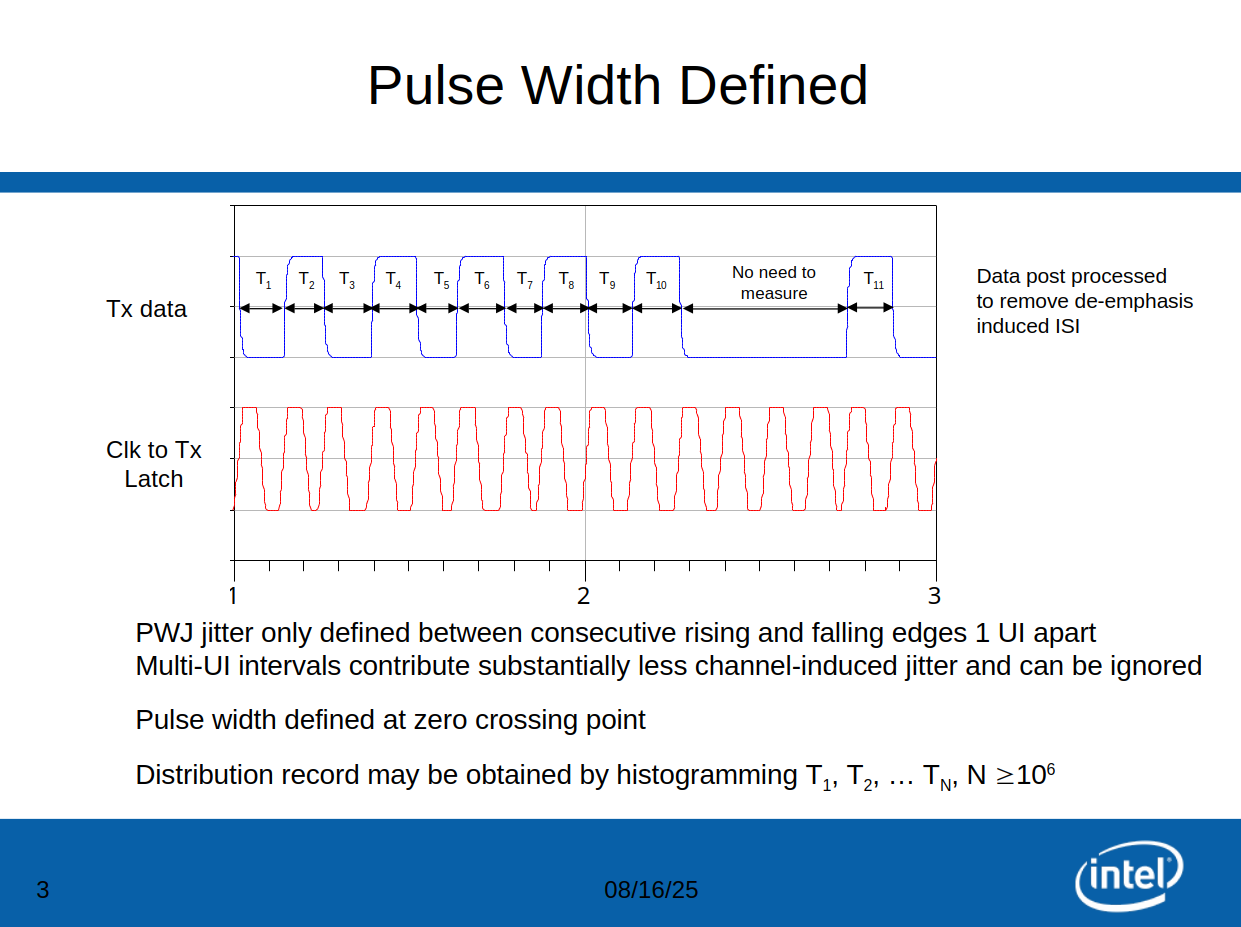
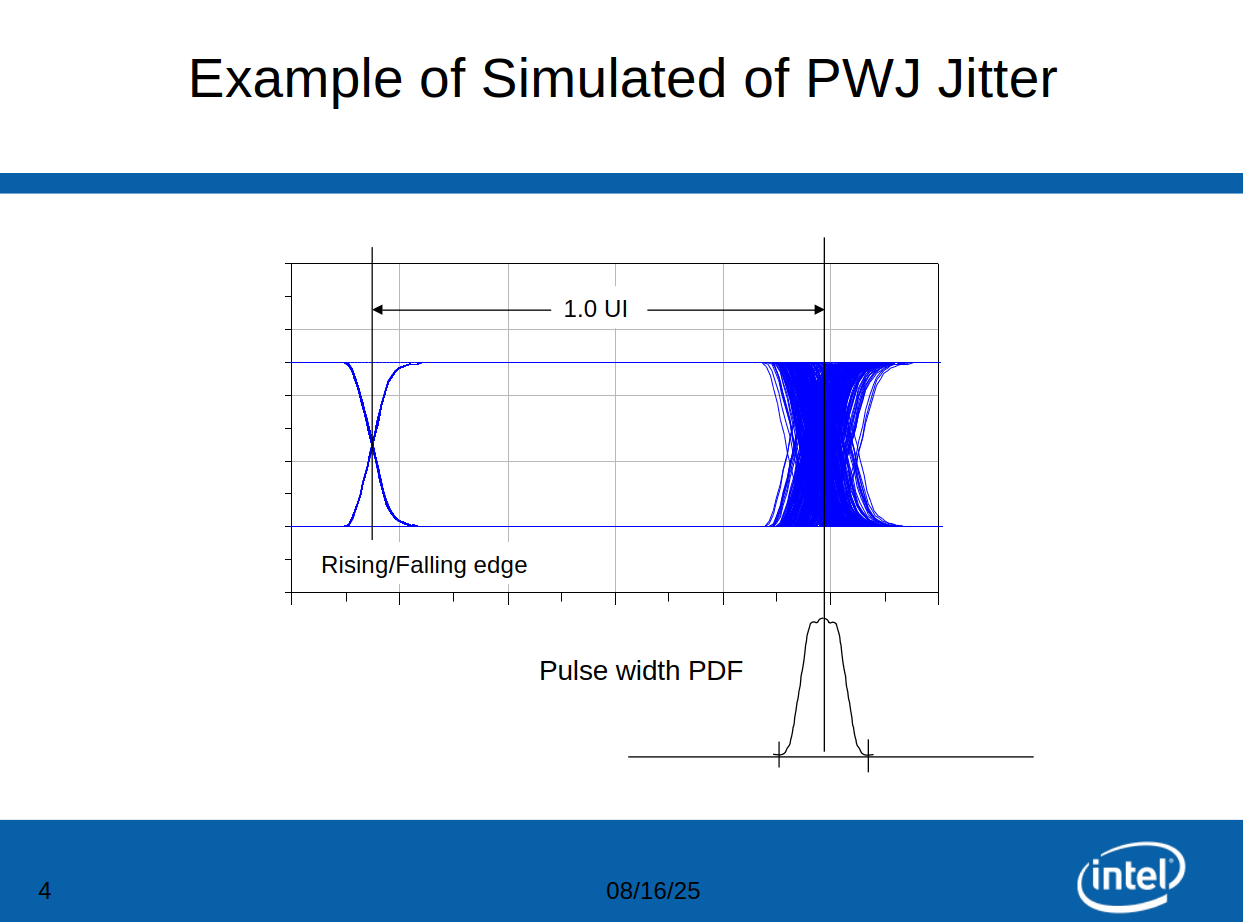
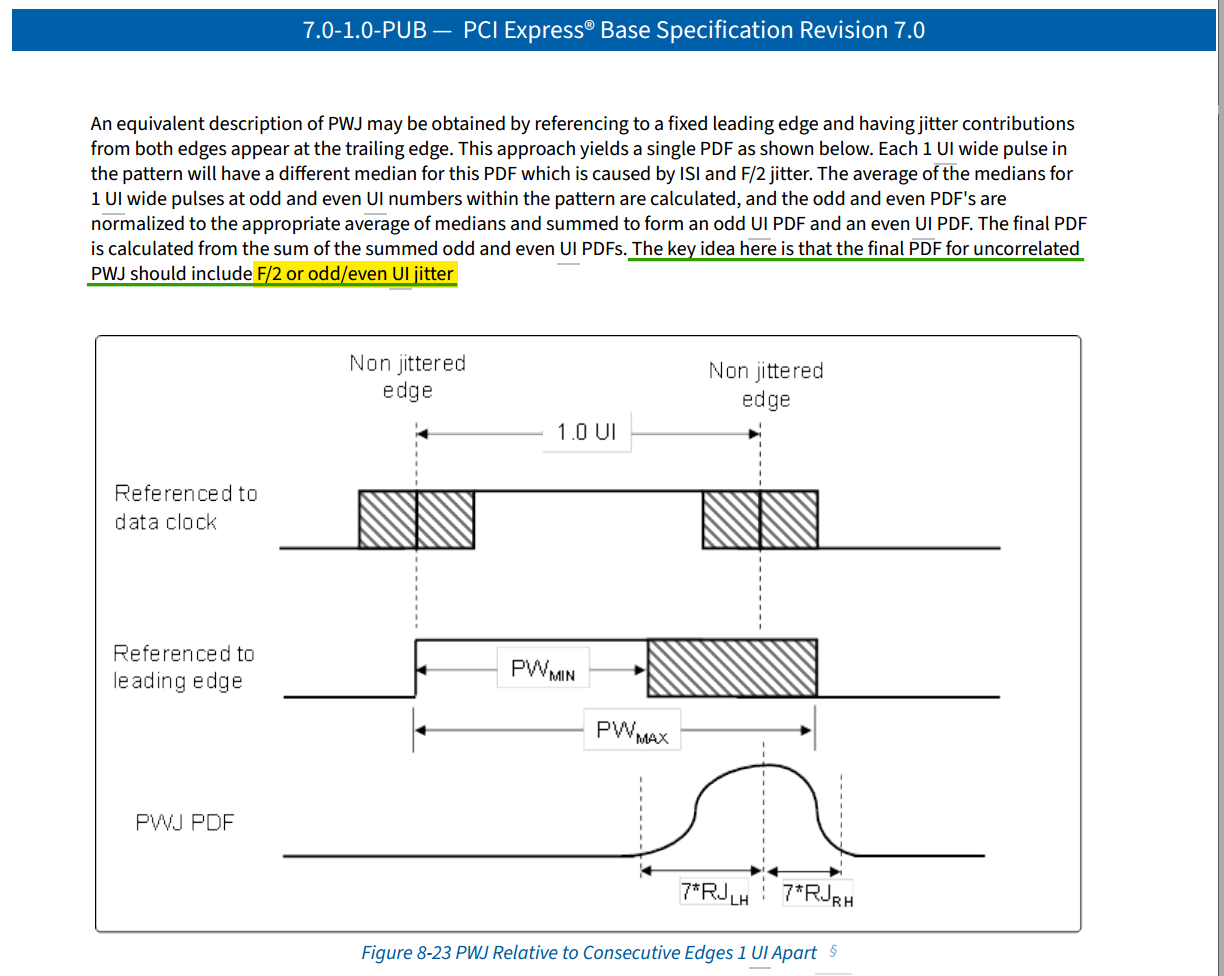
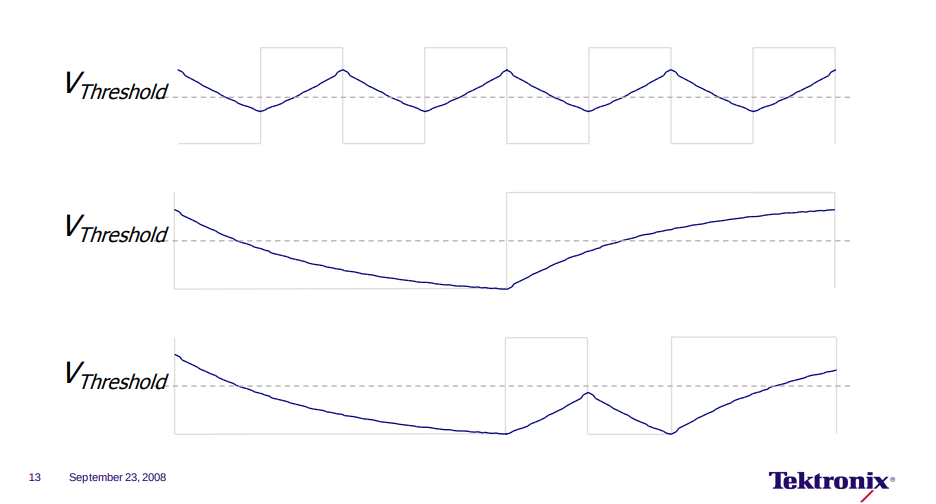
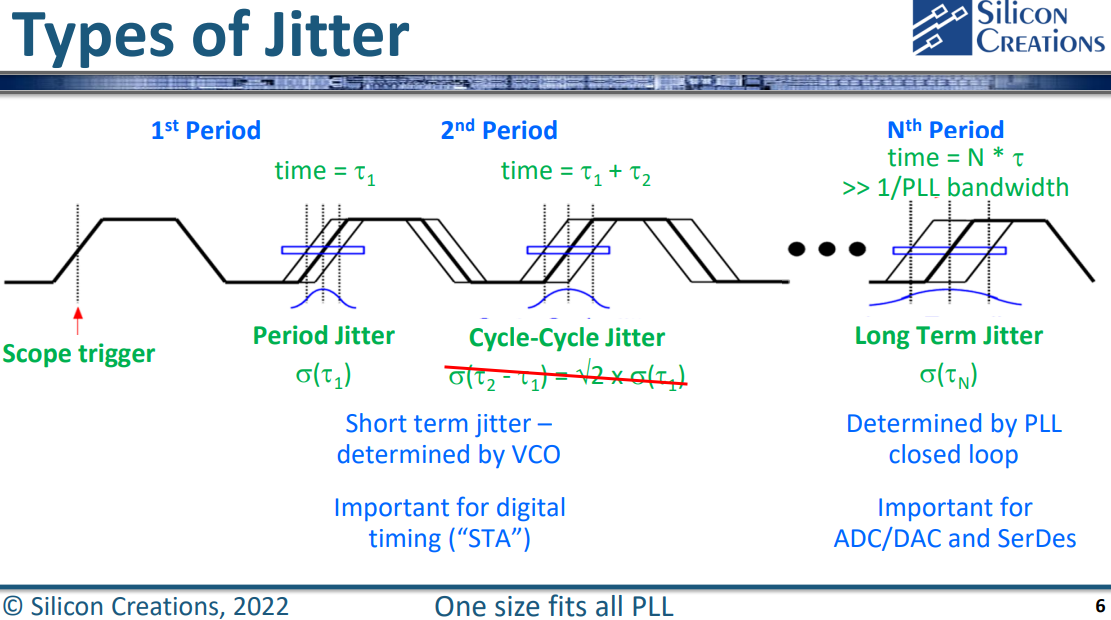
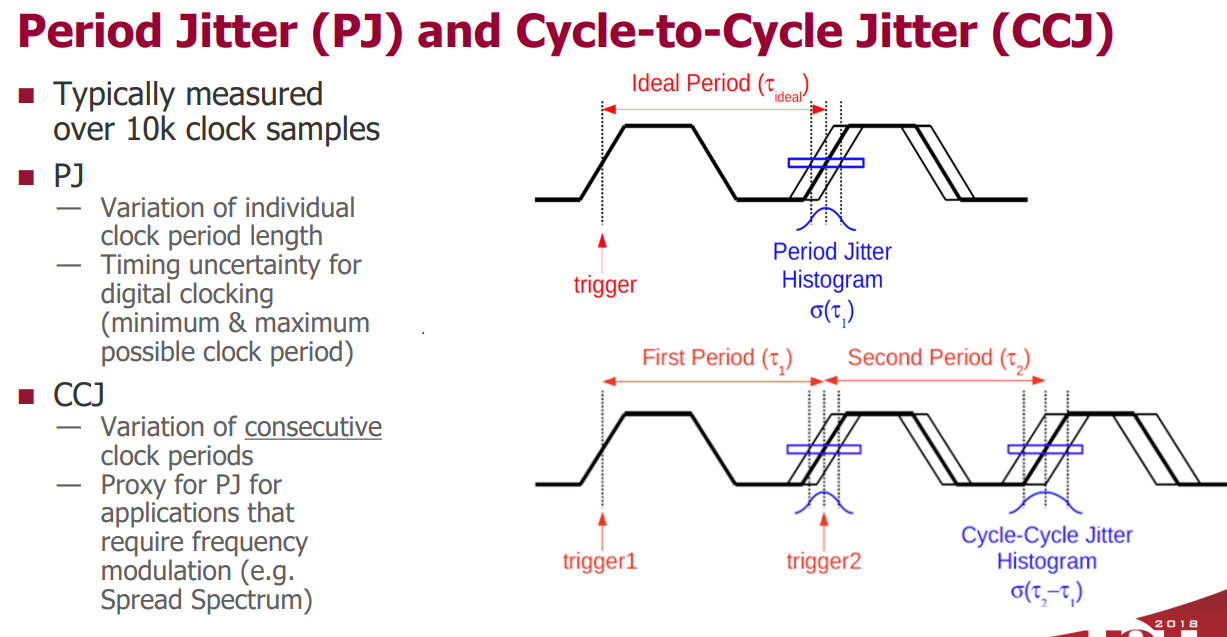
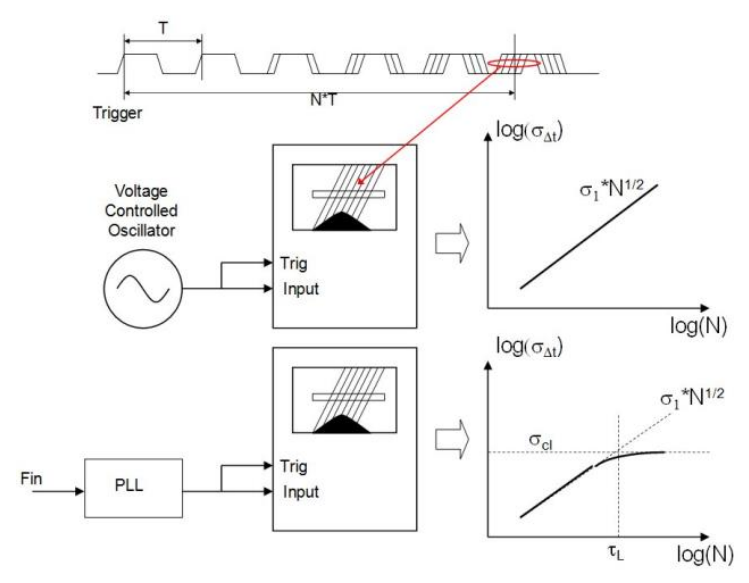
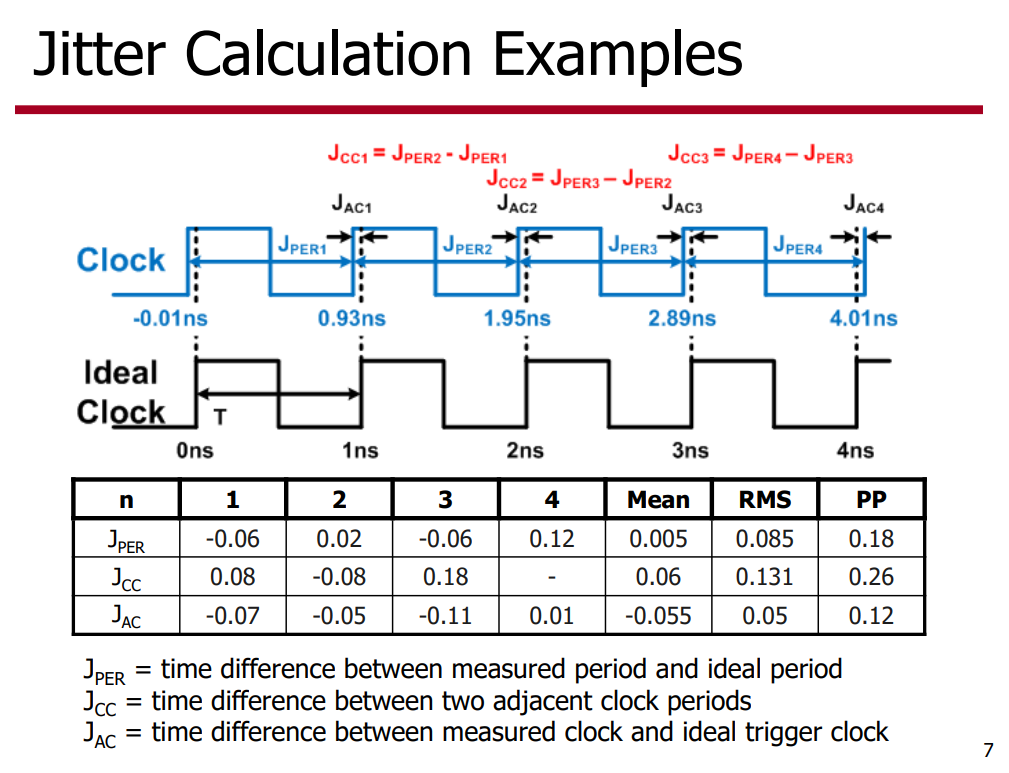
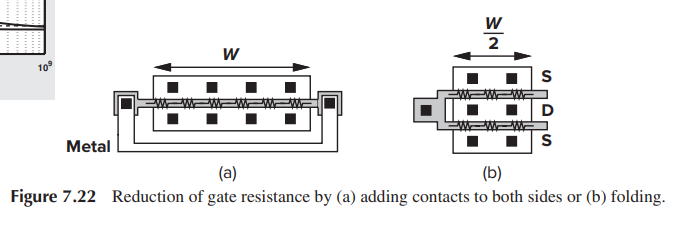
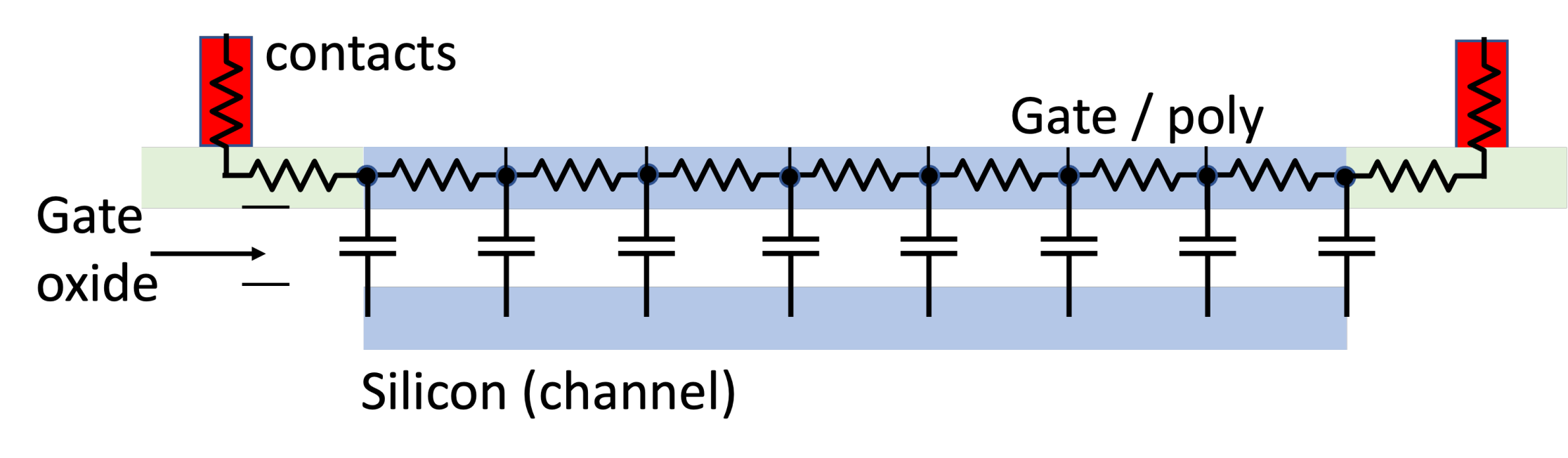
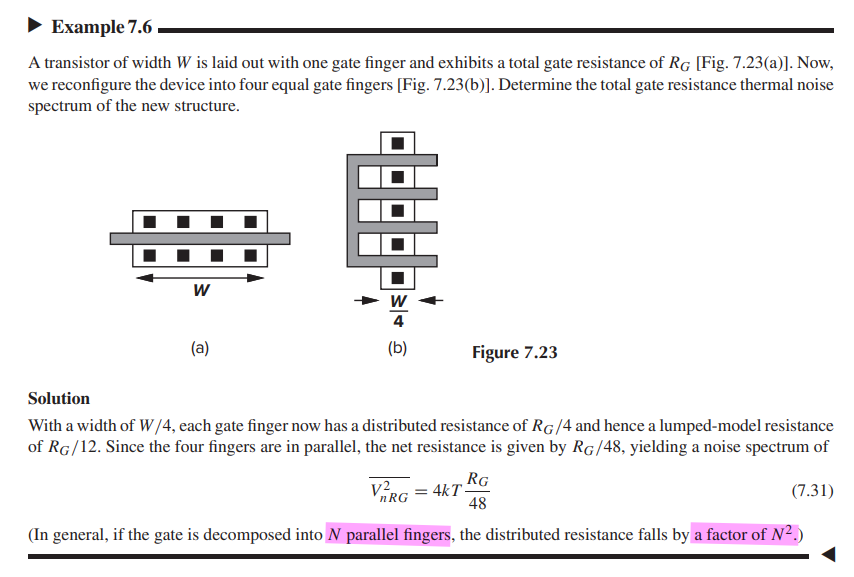
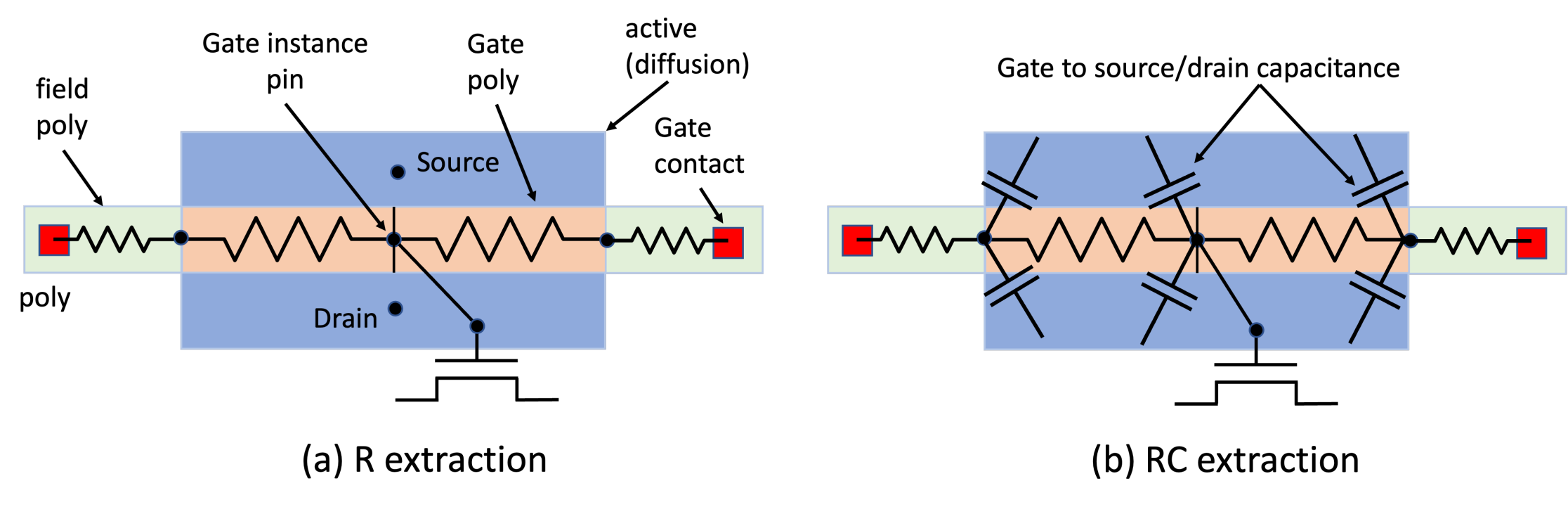
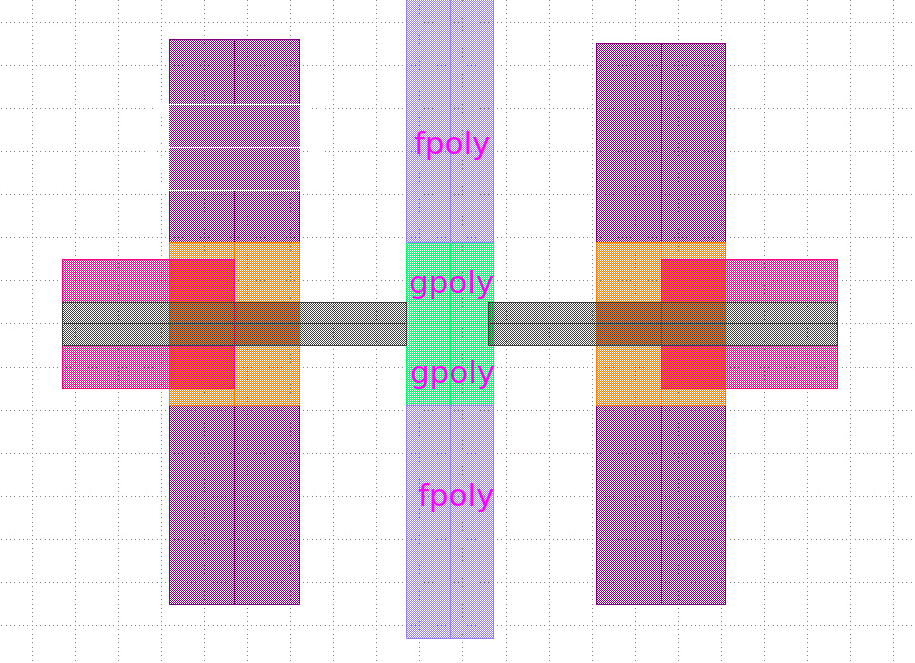
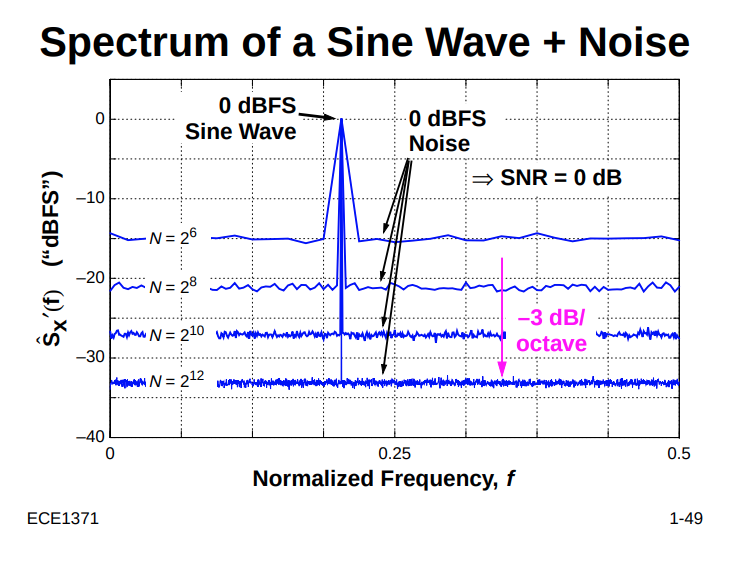
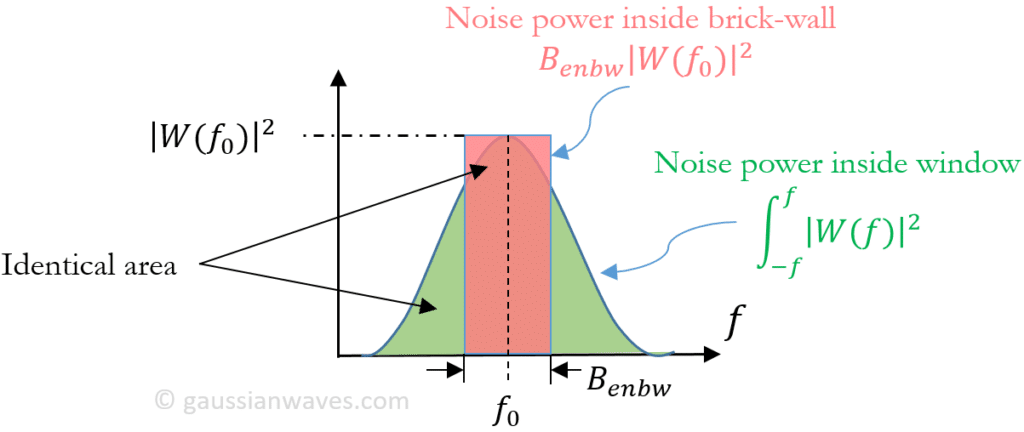
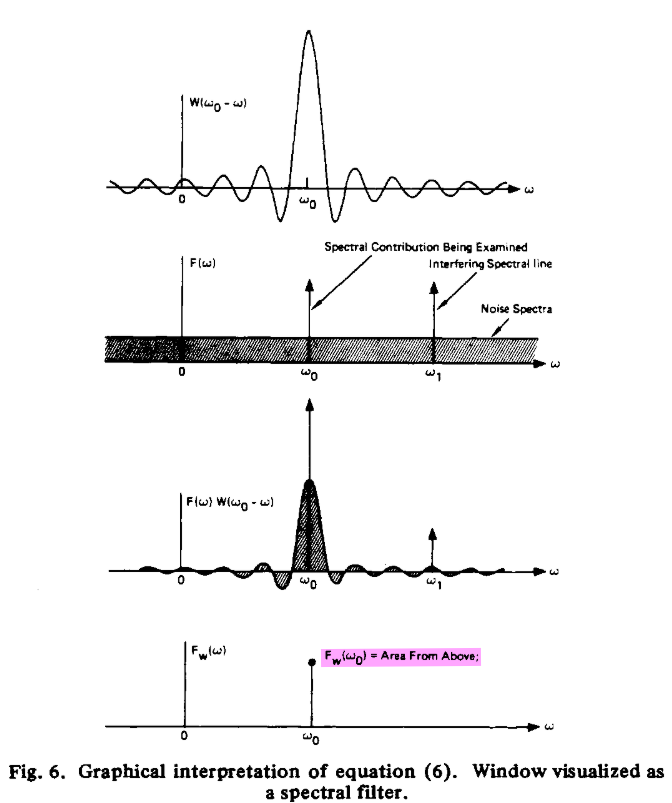
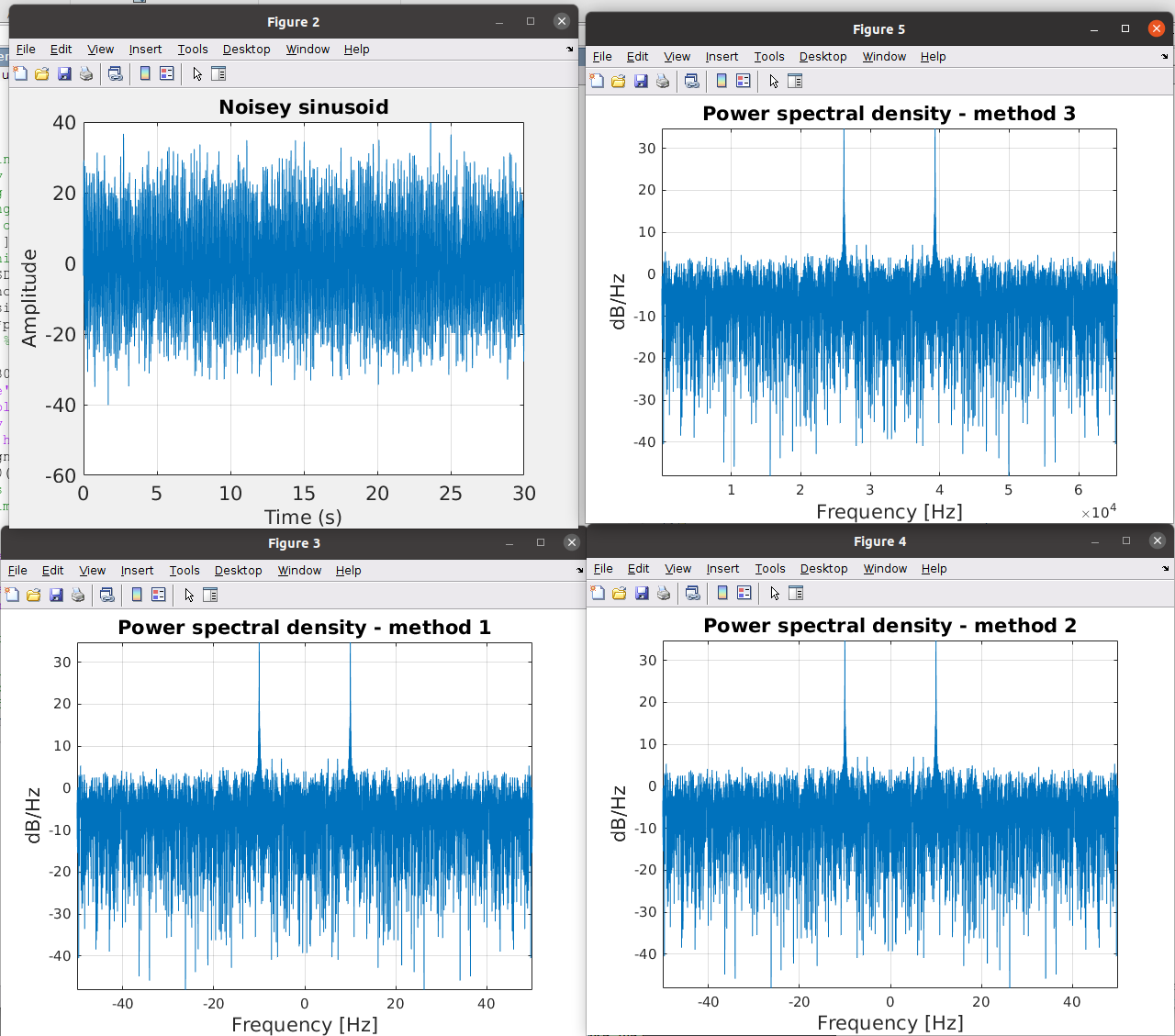
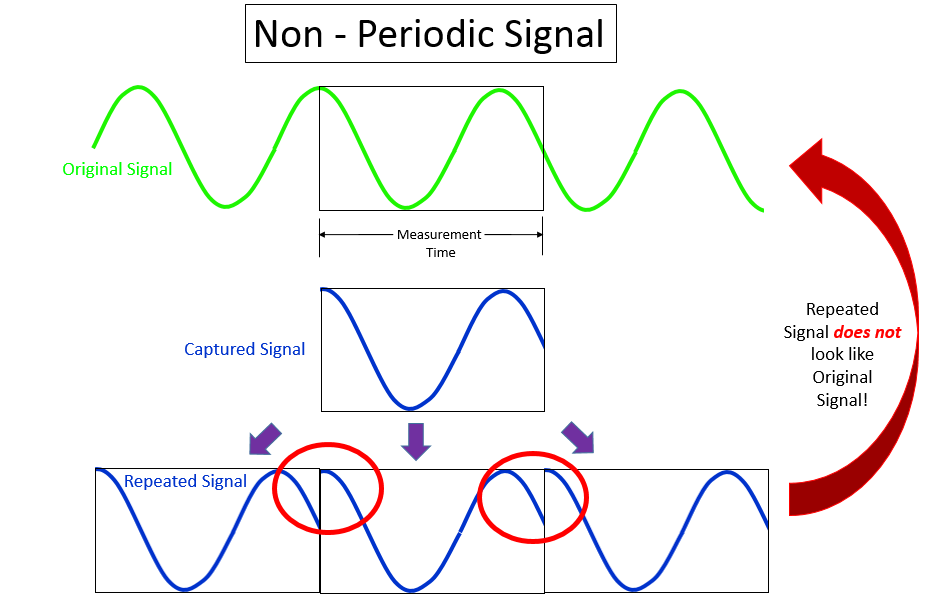
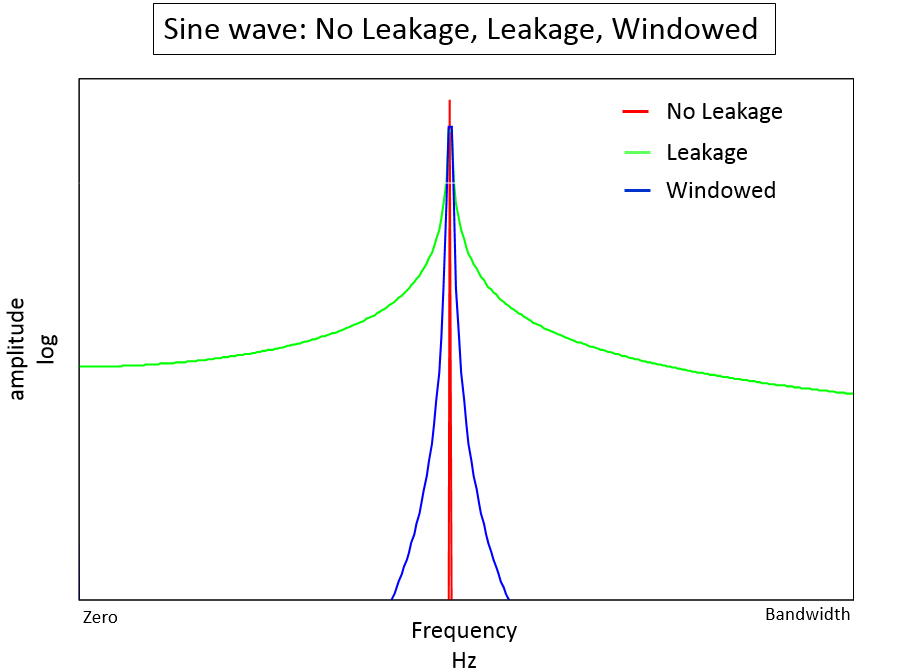
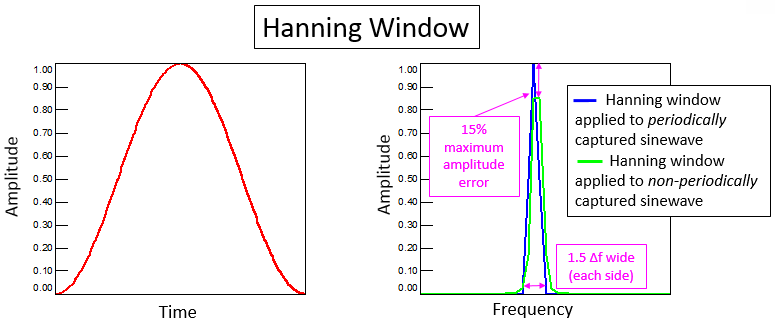
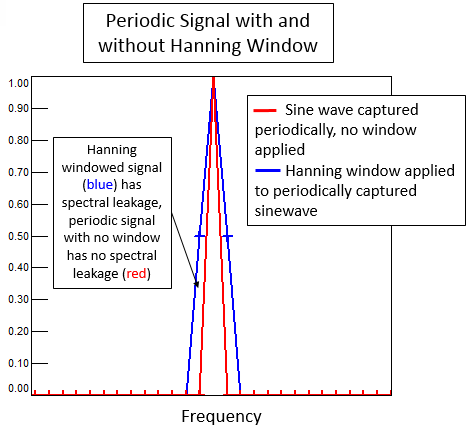
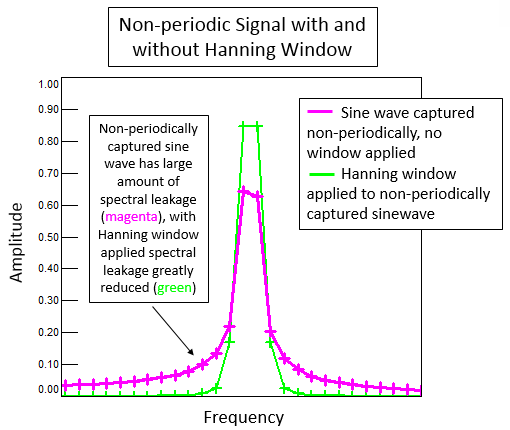
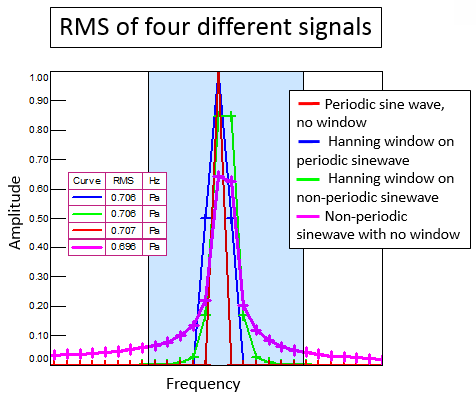
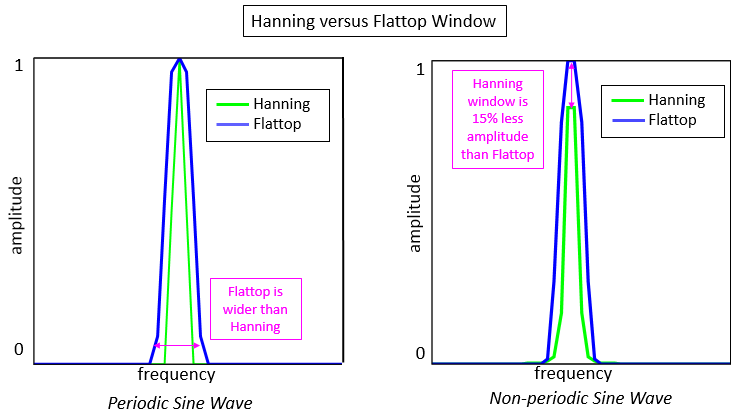
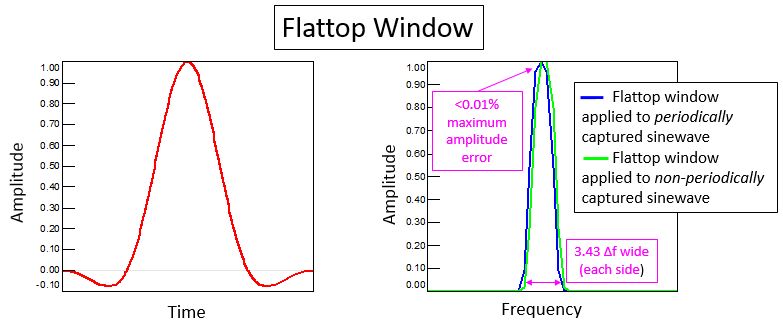
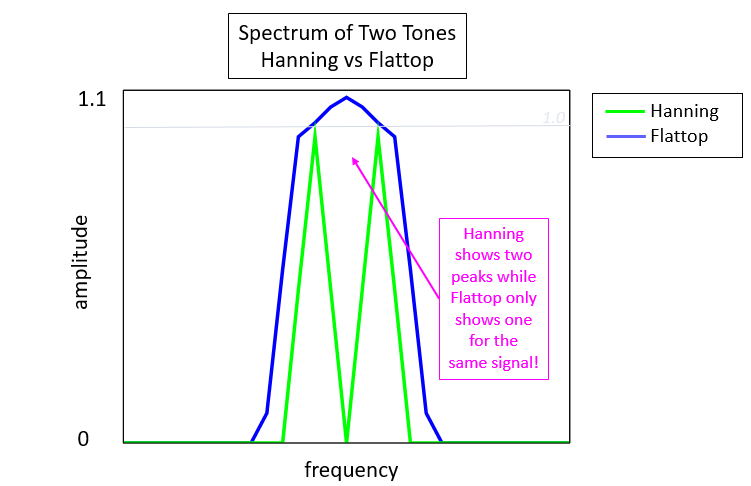
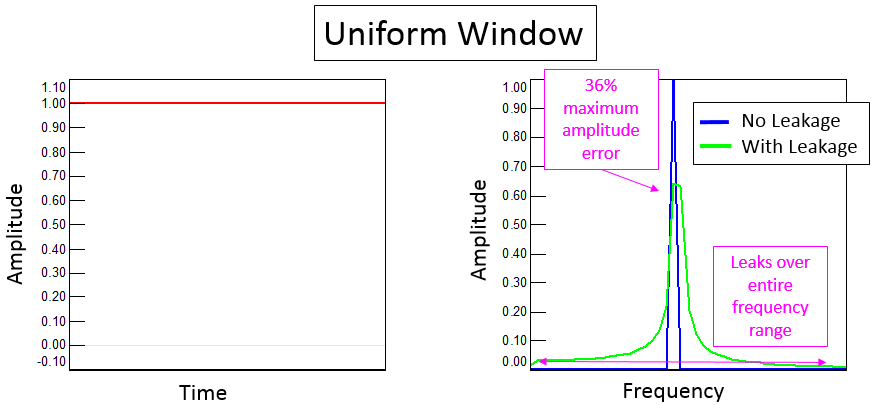
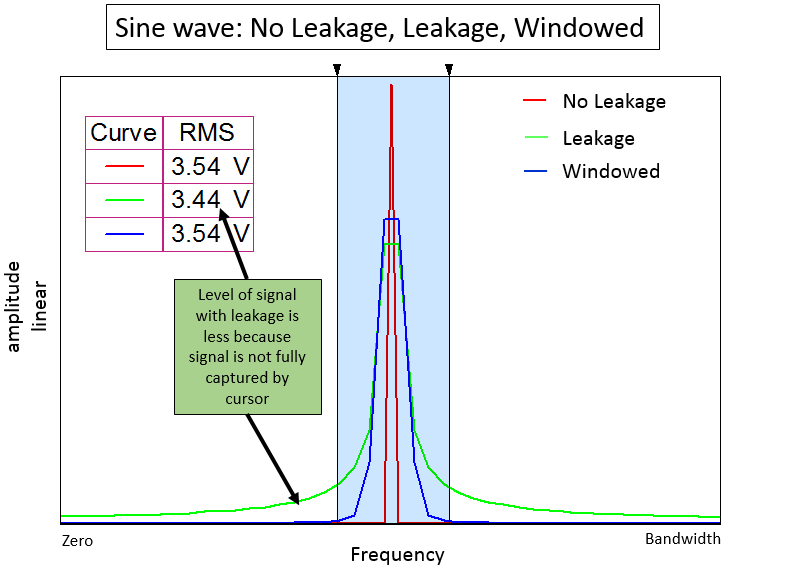
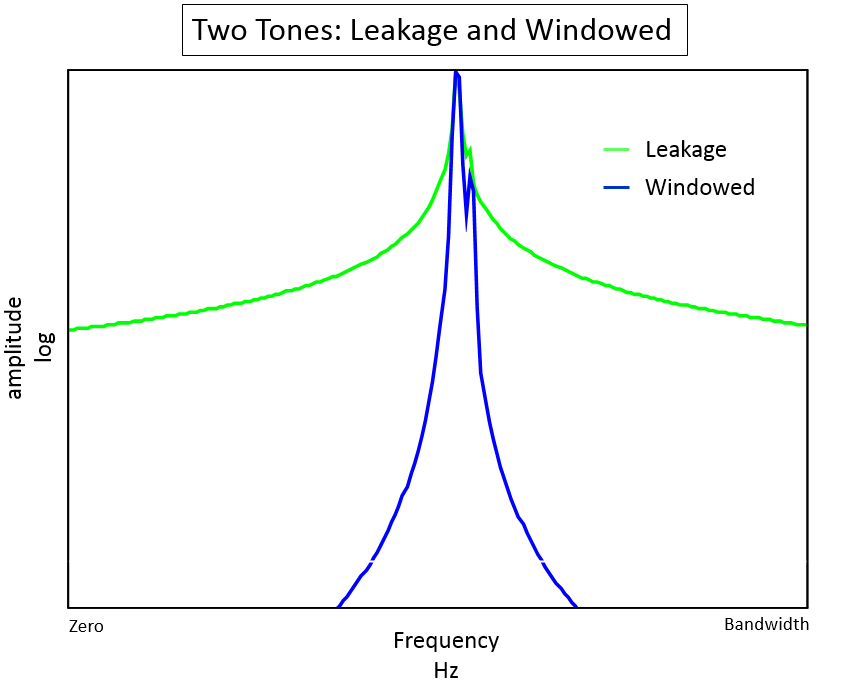
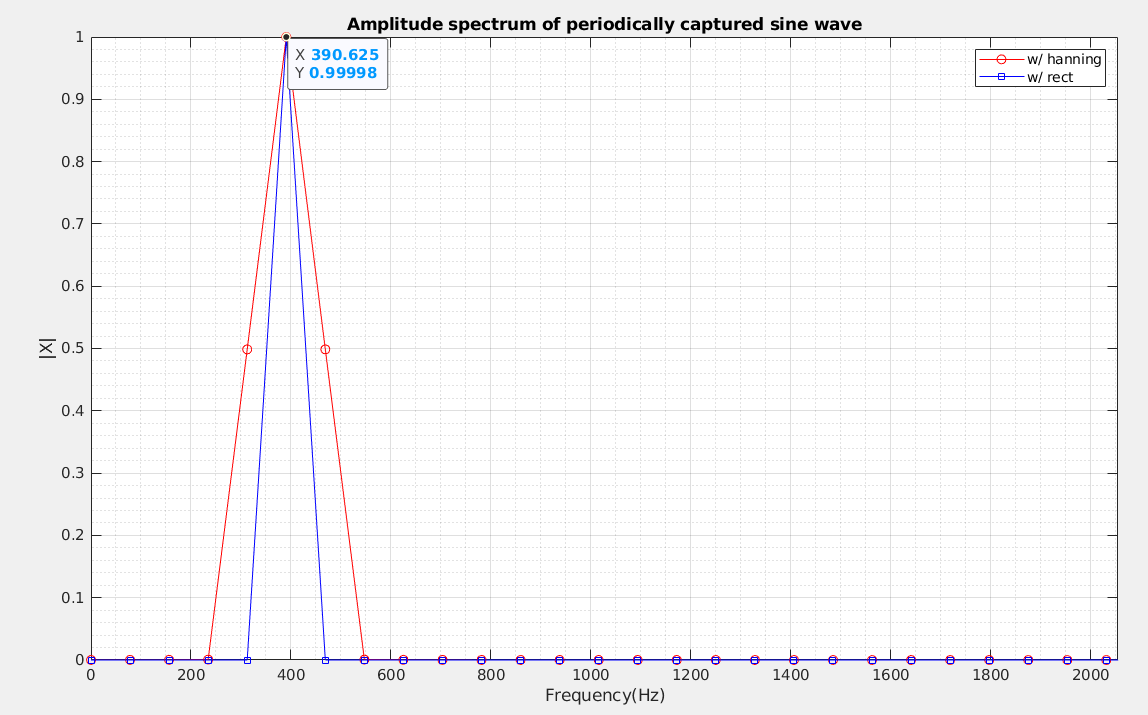
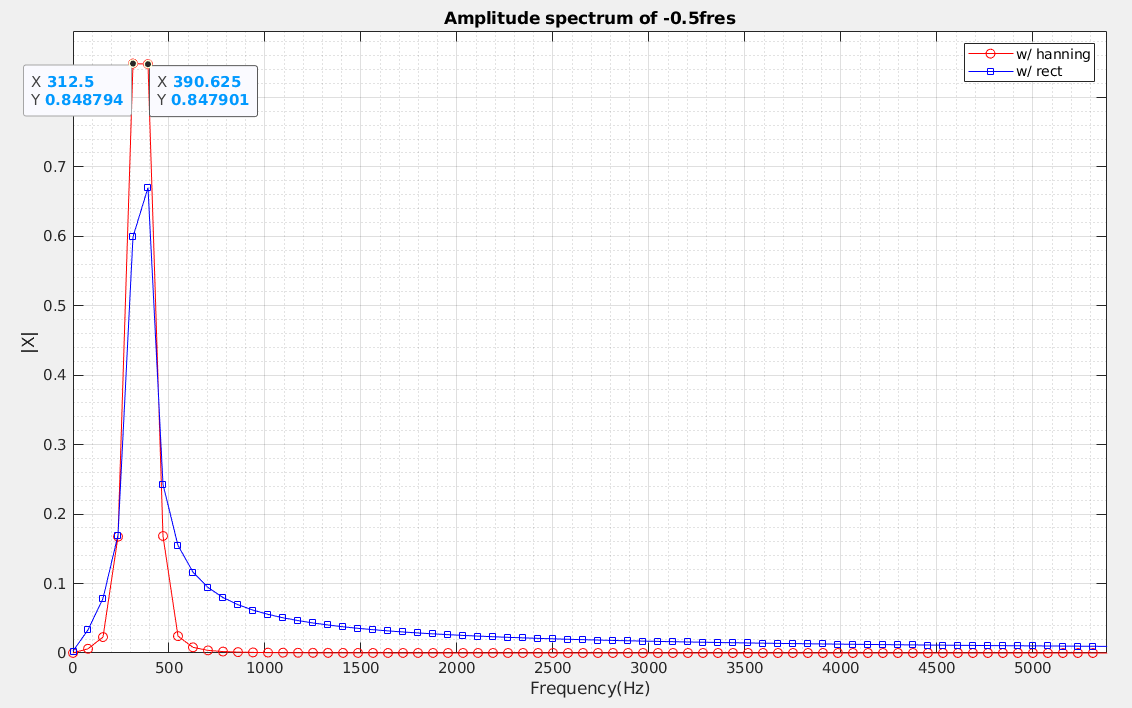
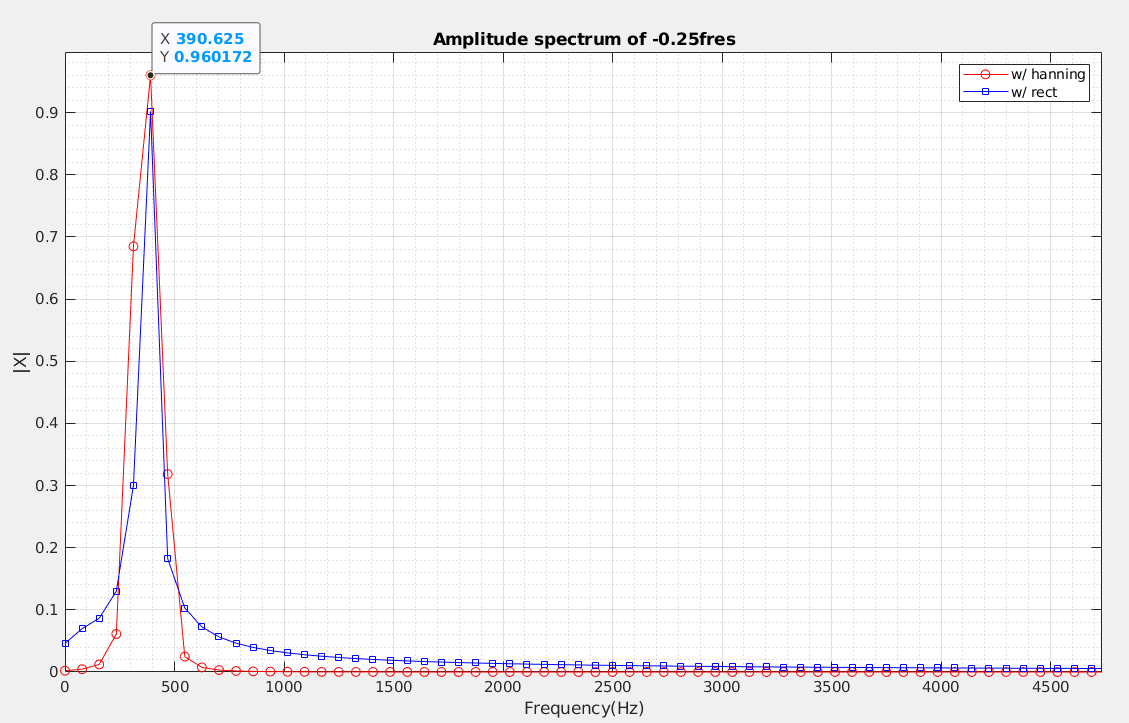
A. A. Abidi, "Phase Noise and Jitter in CMOS Ring Oscillators," in IEEE Journal of Solid-State Circuits, vol. 41, no. 8, pp. 1803-1816, Aug. 2006 [pdf]

Lossless Integral

a noise current integrates onto a capacitor only

With white Gaussian noise at the input, the output spectrum is no longer white although its distribution remains Gaussian

Lossy Integral

a noise current integrates onto a capacitor which is shunted by a finite loss resistance

\[ \frac{V}{I}(s) = \frac{1}{C}\frac{RC}{1+sRC} \overset{\mathcal{L}^{-1}}{\longrightarrow}\frac{1}{C}\cdot e^{-\frac{t}{RC}} \]

Laplace transform of Truncated Impulse Response \(0 \to t_d\) \[ \int_{0}^{t_d}\frac{1}{C}\cdot e^{-\frac{t}{RC}} \cdot e^{-st}dt = \frac{1}{C}\cdot \frac{1}{s+\frac{1}{RC}}\left(1-e^{-(st_d+\theta)}\right)=\frac{1}{C}\cdot \color{red}\frac{t_d}{st_d+\theta}\left(1-e^{-(st_d+\theta)}\right) \]

Google AI Mode [https://share.google/aimode/O6rjWM1YWel0NudI7]

reference

David Herres, The difference between signal under-sampling, aliasing, and folding URL: https://www.testandmeasurementtips.com/the-difference-between-signal-under-sampling-aliasing-and-folding-faq/

Pharr, Matt; Humphreys, Greg. (28 June 2010). Physically Based Rendering: From Theory to Implementation. Morgan Kaufmann. ISBN 978-0-12-375079-2. Chapter 7 (Sampling and reconstruction)

Alan V Oppenheim, Ronald W. Schafer. Discrete-Time Signal Processing, 3rd edition

Mathuranathan Viswanathan. Digital Modulations using Matlab: Build Simulation Models from Scratch

Miller's approximation

Right-Half-Plane Zero

\[ \left[(v_i - v_o)sC_c - g_m v_i\right]R_o = v_o \] Then \[ \frac{v_o}{v_i} = -g_mR_o\frac{1-s\frac{C_c}{g_m}}{1+sR_oC_c} \] right-half-plane Zero \(\omega _z = \frac{g_m}{C_c}\)

Equivalent cap

The amplifier gain magnitude \(A_v = g_m R_o\) \[ I_\text{c,in} = (v_i - v_o)sC_c \] Then \[\begin{align} I_\text{c,in} &= (v_i + A_v v_i)sC_c \\ & = v_i s (1+A_v)C_c \end{align}\]

we get \(C_\text{in,eq}= (1+A_v)C_c\simeq A_vC_c\)

Similarly \[\begin{align} I_\text{c,out} &= (v_o - v_i)sC_c \\ & = v_o s (1+\frac{1}{A_v})C_c \end{align}\]

we get \(C_\text{out,eq}= (1+\frac{1}{A_v})C_c\approx C_c\)

Pole Splitting

Generic circuit in textbook

In addition to lowering the required capacitor value, Miller compensation entails a very important property: it moves the output pole away from the origin. This effect is called pole splitting

The 1st stage is replaced with Thevenin equivalent circuit , \(V_i \approx V_i \cdot g_{m1}R_{o1}\)

\[\begin{align} \frac{V_i-V_{o1}}{R_{o1}} &= V_{o1}\cdot sC_{o1}+(V_{o1}-V_o)\cdot sC_c \\ V_{o1} &= \frac{V_i+sR_{o1}C_cV_o}{1+sR_{o1}(C_{o1}+C_c)} \end{align}\] \[ (V_{o1}-V_o)sC_c=g_{m2}V_{o1}+V_o(\frac{1}{R_{o2}+sC_L}) \] substitute \(V_{o1}\), we get

\[\begin{align} \frac{V_o}{V_i} &= \frac{(sC_c-g_{m2})R_{o2}}{s^2R_{o1}R_{o2}(C_cC_{o1}+C_LC_{o1}+C_LC_c)+s\left\{ R_{o1}C_c\cdot g_{m2}R_{o2}+R_{o2}(C_c+C_L)+R_{o1}(C_{o1}+C_c) \right\} +1} \\ &= \frac{g_{m2}R_{o2}(s\frac{C_c}{g_{m2}}-1)}{s^2R_{o1}R_{o2}(C_cC_{o1}+C_LC_{o1}+C_LC_c)+s\left\{ R_{o1}C_c\cdot g_{m2}R_{o2}+R_{o2}(C_c+C_L)+R_{o1}(C_{o1}+C_c) \right\} +1} \end{align}\]

left hand plane poles

\[\begin{align} \omega_1 &= \frac{1}{R_{o1}C_c\cdot g_{m2}R_{o2}+R_{o2}(C_c+C_L)+R_{o1}(C_{o1}+C_c)} \\ \omega_2 &= \frac{R_{o1}C_c\cdot g_{m2}R_{o2}+R_{o2}(C_c+C_L)+R_{o1}(C_{o1}+C_c)}{R_{o1}R_{o2}(C_cC_{o1}+C_LC_{o1}+C_LC_c)} \end{align}\]

and RHP (right-hand plane) zero \[ \omega_z=\frac{g_{m2}}{C_c} \]

with series switch

replace \(sC_L\) with \(1/(R_{sw}+\frac{1}{sC_L})\) \[\begin{align} \frac{V_{o2}}{V_i} &= \frac{g_{m2}R_{o2}(s\frac{C_c}{g_{m2}}-1)(1+sR_{sw}C_L)}{s^3R_{o1}R_{o2}R_{sw}C_{o1}C_cC_L+s^2\left\{R_{o1}R_{o2}(C_cC_{o1}+C_LC_{o1}+C_LC_c)+ \left[ R_{o1}C_c\cdot g_{m2}R_{o2}+R_{o2}(C_c+0)+R_{o1}(C_{o1}+C_c)\right]R_{sw}C_L \right\}+s\left\{ R_{o1}C_c\cdot g_{m2}R_{o2}+R_{o2}(C_c+C_L)+R_{o1}(C_{o1}+C_c) +R_{sw}C_L\right\} +1} \end{align}\] Due to \[ \frac{V_o}{V_{o2}} = \frac{\frac{1}{sC_L}}{R_{sw}+\frac{1}{sC_L}}=\frac{1}{1+sR_{sw}C_L} \] Then \[\begin{align} \frac{V_o}{V_i} &= \frac{V_{o2}}{V_i} \cdot \frac{V_o}{V_{o2}} \\ &= \frac{g_{m2}R_{o2}(s\frac{C_c}{g_{m2}}-1)}{s^3R_{o1}R_{o2}R_{sw}C_{o1}C_cC_L+s^2\left\{R_{o1}R_{o2}(C_cC_{o1}+C_LC_{o1}+C_LC_c)+ \left[ R_{o1}C_c\cdot g_{m2}R_{o2}+R_{o2}(C_c+0)+R_{o1}(C_{o1}+C_c)\right]R_{sw}C_L \right\}+s\left\{ R_{o1}C_c\cdot g_{m2}R_{o2}+R_{o2}(C_c+C_L)+R_{o1}(C_{o1}+C_c) +R_{sw}C_L\right\} +1} \end{align}\]

\(R_{sw}\) & \(R_c\)

\[\begin{align} \frac{V_{o2}}{V_i} &=-g_{m2}R_{o2}\frac{sC_c(R_c-1/g_{m2})+1}{(1+sR_{o1}C_{o1})sR_{o2}C_c+sR_{o1}\cdot g_{m2}R_{o2}C_c+\frac{s(R_{o2}+R_{sw})C_L+1}{sR_{sw}C_L+1}\left[(1+sR_{o1}C_{o1})(1+sR_cC_c)+sR_{o1}C_c \right]} \\ &=-g_{m2}R_{o2}\frac{sC_c(R_c-1/g_{m2})+1}{s^2R_{o1}R_{o2}C_{o1}C_c+sR_{o2}C_c+sR_{o1}\cdot g_{m2}R_{o2}C_c+\frac{s(R_{o2}+R_{sw})C_L+1}{sR_{sw}C_L+1}\left[(1+sR_{o1}C_{o1})(1+sR_cC_c)+sR_{o1}C_c \right]} \\ &=-g_{m2}R_{o2}\frac{\left[ sC_c(R_c-1/g_{m2})+1 \right](sR_{sw}C_L+1)}{s^2R_{o1}R_{o2}C_{o1}C_c(sR_{sw}C_L+1)+sR_{o2}C_c(sR_{sw}C_L+1)+sR_{o1}\cdot g_{m2}R_{o2}C_c(sR_{sw}C_L+1)+\left[s(R_{o2}+R_{sw})C_L+1\right]\left[(1+sR_{o1}C_{o1})(1+sR_cC_c)+sR_{o1}C_c \right]} \end{align}\]

\(s^3\) terms in denominator \[ H_3 = s^3\cdot(R_{o1}R_{o2}R_c+R_{o1}R_{o2}R_{sw} +R_{o1}R_cR_{sw})\cdot C_{o1}C_cC_L \] \(s^2\) terms in denominator \[\begin{align} H_2 &=s^2\cdot(R_{o1}R_{o2}C_{o1}C_c+R_{o1}R_{o2}C_{o1}C_L+R_{o2}R_cC_cC_L+R_{o1}R_{o2}C_cC_L+R_{o1}R_cC_{o1}C_c\\ &+R_{o2}R_{sw}C_cC_L+R_{o1}R_{sw}C_cC_L\cdot g_{m2}R_{o2}+R_{o1}R_{sw}C_{o1}C_L+R_{sw}R_cC_cC_L+R_{o1}R_{sw}C_cC_L) \end{align}\]

\(s^1\) term in denominator \[ H_1=s(R_{o1}\cdot g_{m2}R_{o2}C_c+R_{o1}C_{o1}+R_cC_c+R_{o1}C_c+R_{o2}C_c+R_{o2}C_L+R_{sw}C_L) \] \(s^0\) term in denominator \[ H_0=1 \] set \(R_c=0\) and \(R_{sw}=0\), the \(H_*\) reduced to \[\begin{align} H_3 &= 0 \\ H_2 &=s^2R_{o1}R_{o2}(C_{o1}C_c+C_{o1}C_L+C_cC_L) \\ H_1&=s(R_{o1}\cdot g_{m2}R_{o2}C_c+R_{o1}C_{o1}+R_{o1}C_c+R_{o2}C_c+R_{o2}C_L) \\ H_0&=1 \end{align}\] That is \[ H=s^2R_{o1}R_{o2}(C_{o1}C_c+C_{o1}C_L+C_cC_L)+s(R_{o1}\cdot g_{m2}R_{o2}C_c+R_{o1}C_{o1}+R_{o1}C_c+R_{o2}C_c+R_{o2}C_L)+1 \]

which is same with our previous analysis of Generic circuit in textbook

And we know \[ \frac{V_o}{V_{o2}}=\frac{1}{1+sR_{sw}C_L} \] Finally, we get \(\frac{V_o}{V_i}\) \[\begin{align} \frac{V_o}{V_i} &= \frac{V_{o2}}{V_i} \cdot \frac{V_o}{V_{o2}} \\ &= -g_{m2}R_{o2}\frac{\left[ sC_c(R_c-1/g_{m2})+1 \right](sR_{sw}C_L+1)}{H_3+H_2+H_1+1} \cdot \frac{1}{1+sR_{sw}C_L} \\ &= -g_{m2}R_{o2}\frac{ sC_c(R_c-1/g_{m2})+1}{H_3+H_2+H_1+1} \end{align}\]

The loop transfer function is \[ \frac{V_o}{V_i} =-g_{m1}R_{o1}g_{m2}R_{o2}\frac{ sC_c(R_c-1/g_{m2})+1}{H_3+H_2+H_1+1} \]

vccs model

simplify the transfer function

1. omit \(C_{o1}\)

We omit \(C_{o1}\) in frequency range of interest

\[\begin{align} H_3 &= 0 \\ H_2 &=s^2(R_{o2}R_c+R_{o1}R_{o2}+R_{o2}R_{sw}+R_{o1}R_{sw}\cdot g_{m2}R_{o2}+R_{sw}R_c+R_{o1}R_{sw})\cdot C_cC_L \\ H_1 &=s(R_{o1}\cdot g_{m2}R_{o2}C_c+R_cC_c+R_{o1}C_c+R_{o2}C_c+R_{o2}C_L+R_{sw}C_L) \\ H_0 &= 1 \end{align}\]

two poles and 1 zero

2. more simplification

Then, some terms can be omitted

\[\begin{align} H_2 &=s^2R_{o1}R_{o2}(1+g_{m2}R_{sw})\cdot C_cC_L \\ H_1 &=sR_{o1}\cdot g_{m2}R_{o2}C_c \\ H_0 &= 1 \end{align}\]

The poles can be deduced \[\begin{align} \omega_1 &= \frac{1}{R_{o1}\cdot g_{m2}R_{o2}C_c} \\ \omega_2 &= \frac{1}{1+g_{m2}R_{sw}}\cdot \frac{g_{m2}}{C_L} \\ &= \frac{1}{(g_{m2}^{-1}+R_{sw})C_L} \end{align}\]

The pole \(\omega_2=\frac{1}{g_{m2}^{-1}C_L}\) is changed to \(\omega_2=\frac{1}{(g_{m2}^{-1}+R_{sw})C_L}\)

In order to cancel \(\omega_2\) with \(\omega_z\), \(R_c\) shall be increased

\[ R_{eq}=g_{m2}^{-1}+R_{sw} \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

gm1 = 400e-6;
gm2 = 3.2e-3;
Ro1 = 800e3;
Ro2 = 100e3;
Co1 = 100e-15;
CL = 7e-12;
Rc = 15e3;
Cc = 2e-12;
Rsw = 6e3;


s = tf('s');

%%%%%%%%%%%%%%%%%%%%%%%%%%
% org equation
H3 = s^3*(Ro1*Ro2*Rc + Ro1*Ro2*Rsw+Ro1*Rc*Rsw)*Co1*Cc*CL;
H2 = s^2*(Ro1*Ro2*Co1*Cc+Ro1*Ro2*Co1*CL+Ro2*Rc*Cc*CL+Ro1*Ro2*Cc*CL+Ro1*Rc*Co1*Cc+ ...
    Ro2*Rsw*Cc*CL+Ro1*Rsw*Cc*CL*gm2*Ro2+Ro1*Rsw*Co1*CL+Rsw*Rc*Cc*CL+Ro1*Rsw*Cc*CL);
H1 = s*(Ro1*gm2*Ro2*Cc+Ro1*Co1+Rc*Cc+Ro1*Cc+Ro2*Cc+Ro2*CL+Rsw*CL);
Nmt = s*Cc*(Rc-1/gm2)+1;
TF = -gm1*Ro1*gm2*Ro2*Nmt/(H3+H2+H1+1);
[mag, phase, wout] = bode(TF, {100*2*pi, 100*1e9*2*pi});


%%%%%%%%%%%%%%%%%%%%%%%%%%
% omit Co1
H3 = 0;
H2 = s^2*(Ro2*Rc+Ro1*Ro2+Ro2*Rsw+Ro1*Rsw*gm2*Ro2+Rsw*Rc+Ro1*Rsw)*Cc*CL;
H1 = s*(Ro1*gm2*Ro2*Cc+Rc*Cc+Ro1*Cc+Ro2*Cc+Ro2*CL+Rsw*CL);
Nmt = s*Cc*(Rc-1/gm2)+1;
TF = -gm1*Ro1*gm2*Ro2*Nmt/(H3+H2+H1+1);
[mag2, phase2, wout2] = bode(TF, {100*2*pi, 100e9*2*pi});


%%%%%%%%%%%%%%%%%%%%%%%%%%
% more simplification
H3 = 0;
H2 = s^2*Ro1*Ro2*(1+gm2*Rsw)*Cc*CL;
H1 = s*Ro1*gm2*Ro2*Cc;
Nmt = s*Cc*(Rc-1/gm2)+1;
TF = -gm1*Ro1*gm2*Ro2*Nmt/(H3+H2+H1+1);
[mag3, phase3, wout3] = bode(TF, {100*2*pi, 100e9*2*pi});

subplot(2,1,1)
semilogx(wout(:)/2/pi, 20*log10(mag(:)), 'k', 'linewidth', 2);
hold on;
semilogx(wout2(:)/2/pi, 20*log10(mag2(:)), 'ro--', 'linewidth', 2)
semilogx(wout3(:)/2/pi, 20*log10(mag3(:)), 'bs--', 'linewidth', 2)
grid on; title("loop gain (dB)"); xlabel("frequency (Hz)"); legend("original", "Omit C_{o1}", "more simp");

subplot(2,1,2)
semilogx(wout(:)/2/pi, phase(:), 'k', 'linewidth', 2);
hold on;
semilogx(wout2(:)/2/pi, phase2(:), 'ro--', 'linewidth', 2);
semilogx(wout3(:)/2/pi, phase3(:), 'bs--', 'linewidth', 2);
grid on; title("loop phase (Ao)"); xlabel("frequency (Hz)"); legend("original", "Omit C_{o1}", "more simp");

non-dominant pole in Sansen's book

Following demonstrate how derive \(f_{nd}\) from Razavi's equation. We copy \(\omega_2\) here \[ \omega_2 = \frac{R_{o1}C_c\cdot g_{m2}R_{o2}+R_{o2}(C_c+C_L)+R_{o1}(C_{o1}+C_c)}{R_{o1}R_{o2}(C_cC_{o1}+C_LC_{o1}+C_LC_c)} \] which can be reduced as below

\[\begin{align} \omega_2 &= \frac{R_{o1}C_c\cdot g_{m2}R_{o2}+R_{o2}(C_c+C_L)+R_{o1}(C_{o1}+C_c)}{R_{o1}R_{o2}(C_cC_{o1}+C_LC_{o1}+C_LC_c)} \\ &= \frac{R_{o1}C_c\cdot g_{m2}R_{o2}}{R_{o1}R_{o2}(C_cC_{o1}+C_LC_{o1}+C_LC_c)} = \frac{C_c\cdot g_{m2}}{C_cC_{o1}+C_LC_{o1}+C_LC_c} \\ &= \frac{g_{m2}}{C_{o1}+C_L\frac{C_{o1}}{C_c}+C_L} = \frac{g_{m2}}{C_L\frac{C_{o1}}{C_c}+C_L} = \frac{g_{m2}}{C_L} \cdot \frac{1}{1+\frac{C_{o1}}{C_c}} \end{align}\]

Exercise of 2-stage opamp

\(R_{o1}\) and \(R_{o2}\) don't affect stability, if \(f_{nd}>3\text{GBW}\)

DC gain: \(g_{m1}g_{m2}R_{o1}R_{o2}\)

dominant pole: \(\omega_d=\frac{1}{R_{o1}\cdot g_{m2}R_{o2}C_c}\)

\(20log_{10}(1.414^2)=6\text{dB}\)

Ahuja Compensation

This Ahuja compensation topology is popularly known as cascode compensation

The cause of the positive zero is the feedforward current through \(C_m\).

To abolish this zero, we have to cut the feedforward path and create a unidirectional feedback through \(C_m\).

1. Adding a resistor(nulling resistor) is one way to mitigate the effect of the feedforward current.

2. Another approach uses a current buffer cascode to pass the small-signal feedback current but cut the feedforward current

[https://people.eecs.berkeley.edu/~boser/courses/240B/lectures/M07%20OTA%20II.pdf]

王小桃带你读文献. Cascode补偿前传—Ahuja补偿 Ahuja Compensation [https://zhuanlan.zhihu.com/p/1904126782900245880]

—. 两级运放的米勒补偿与Cascode米勒补偿 [https://zhuanlan.zhihu.com/p/10217022358]

The benefits of Ahuja compensation over Miller compensation are severa

• better PSRR

• higher unity-gain bandwidth using smaller compensation capacitor

• ability to cope better with heavy capacitive and resistive loads

Of course, , if the capacitance at the gate of \(M_1\) is taken into account, pole splitting is less pronounced.

including \(r_\text{o2}\)

\[ \frac{V_{out}}{I_{in}} \approx \frac{-g_{m1}R_SR_L(g_{m2}+C_Cs)}{\frac{R_S+r_\text{o2}}{r_\text{o2}}R_LC_LC_Cs^2+g_{m1}g_{m2}R_LR_SC_Cs+g_{m2}} \] The poles as

\[\begin{align} \omega_{p1} &\approx \frac{1}{g_{m1}R_LR_SC_c} \\ \omega_{p2} &\approx \frac{g_{m2}R_Sg_{m1}}{C_L}\frac{r_\text{o2}}{R_S+r_\text{o2}} \end{align}\]

and zero is not affected, which is \(\omega_z =\frac{g_{m2}}{C_C}\)

the above model simulation result is shown below

the zero is located between two poles

take into the capacitance at the gate of \(M_1\) and all other second-order effect

intuitive analysis of zero

miller compensation

• zero in the right half plane \[ g_\text{m1}V_P = sC_c V_P \]

cascode compensation

• zero in the left half plane \[ g_\text{m2}V_X = - sC_c V_X \]

Mitigate Impact of Zero

dominant pole \[ \omega_\text{p,d} = \frac {1} {R_\text{eq}g_\text{m9}R_{L}C_{c}} \] first nondominant pole \[ \omega_\text{p,nd} = \frac {g_\text{m4}R_\text{eq}g_\text{m9}} {C_L} \] zero \[ \omega_\text{z} = (g_\text{m4}R_\text{eq})(\frac {g_\text{m9}} {C_c}) \] a much greater magnitude than \(g_\text{m9}/C_C\)

ahuja variations

Pole-Zero Compensation

Pole-Zero Compensation is also known as Lead Compensation, Parallel Compensation

Note: The dominant pole is at output of the first stage, i.e. \(\frac{1}{R_{EQ}C_{EQ}}\).

Pole & Zero in transfer function

Design with operational amplifiers and analog integrated circuits / Sergio Franco, San Francisco State University. – Fourth edition

\[ Y = \frac{1}{R_1} + sC_1+\frac{1}{R_c+1/SC_c} \]

\[\begin{align} Z &= \frac{1}{\frac{1}{R_1} + sC_1+\frac{1}{R_c+1/SC_c}} \\ &= \frac{R_1(1+sR_cC_c)}{s^2R_1C_1R_cC_c+s(R_1C_c+R_1C_1+R_cC_c)+1} \end{align}\] If \(p_{1c} \ll p_{3c}\), two real roots can be found \[\begin{align} p_{1c} &= \frac{1}{R_1C_c+R_1C_1+R_cC_c} \\ p_{3c} &= \frac{R_1C_c+R_1C_1+R_cC_c}{R_1C_1R_cC_c} \end{align}\]

The additional zero is \[ z_c = \frac{1}{R_cC_c} \] Given \(R_c \ll R\) and \(C_c \gg C\) \[\begin{align} p_{1c} &\simeq \frac{1}{R_1(C_c+C_1)} \simeq \frac{1}{R_1C_c}\\ p_{3c} &= \frac{1}{R_cC_1}+\frac{1}{R_cC_c}+\frac{1}{R_1C_1} \simeq \frac{1}{R_cC_1} \end{align}\]

The output pole is unchanged, which is \[ p_2 = \frac{1}{R_LC_L} \] We usually cancel \(p_2\) with \(z_c\), i.e. \[ R_cC_c=R_LC_L \]

Phase margin

unity-gain frequency \(\omega_t\) \[ \omega_t = A_\text{DC}\cdot P_{1c} =\frac{g_{m1}g_{m2}R_L}{C_c} \]

1. PM=45\(^o\) \[ p_{3c} = \omega_t \] Then, \(C_c\) and \(R_c\) can be obtained

   \[\begin{align} R_c &= \sqrt{\frac{R_1}{C_1\cdot A_{DC}\cdot p_2}}=\sqrt{\frac{R_1\cdot R_LC_L}{C_1\cdot A_{DC}}} \\ C_c &= \sqrt{\frac{A_{DC}\cdot C_1}{R_1\cdot p_2}}=\sqrt{\frac{A_{DC}\cdot C_1 \cdot R_LC_L}{R_1}} \end{align}\]

2. PM=60\(^o\) \[ p_{3c} = 2\cdot\omega_t \] Then, \(C_c\) and \(R_c\) can be obtained \[\begin{align} R_c &= \sqrt{\frac{R_1}{C_1\cdot 2A_{DC}\cdot p_2}} = \sqrt{\frac{R_1\cdot R_LC_L}{C_1\cdot 2A_{DC}}} \\ &= \sqrt{\frac{C_L}{2g_{m1}g_{m2}C_1}}\\ C_c &= \sqrt{\frac{2A_{DC}\cdot C_1}{R_1\cdot p_2}} = \sqrt{\frac{2A_{DC}\cdot C_1 \cdot R_LC_L}{R_1}} \\ &= R_L\sqrt{2g_{m1}g_{m2}C_1C_L} \end{align}\]

   for the unity-gain frequency \(\omega_t\) we find \[ \omega_t = \sqrt{\frac{1}{2}\cdot \frac{g_{m1}g_{m2}}{C_1C_L}} \] The parallel compensation shows a remarkably good result. The new 0 dB frequency lies only a factor \(\sqrt{2}\) lower than the theoretical maximum

To increase \(\phi_m\), we need to raise \(C_c\) a bit while lowering \(R_c\) in proportion in order to maintain pole-zero cancellation. This causes \(p_{1c}\) and \(p_{3c}\) to split a bit further apart.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

clc;
clear;

fd = 84*1e3;	% dominant freq, unit: Hz
fnd = 3.25*1e6;	% unit: Hz
C = 478*1e-15;
R = 1/fd/(2*pi)/C;
Adc = 10^(80/20);

ri = 2; % PM=45: 1;  PM=60: 2
Rc = (R/C/fnd/2/pi/ri/Adc)^0.5; % compensation resistor
Cc = (ri*Adc*C/fnd/2/pi/R)^0.5; % compensation capacitor

wzc = 1/2/pi/Rc/Cc; % zero frequency

ECEN 457 (ESS). Op-Amps Stability and Frequency Compensation Techniques [https://people.engr.tamu.edu/s-sanchez/457%20Stability%20Final.pdf]

Pole-Zero Doublet

The denominator part of \(H_{closed}(s)\) is \[ D(s) = \frac{s^2}{(A_0+1)\omega_{p1}\omega_{p2}}+\frac{\frac{1}{\omega_{p1}} + \frac{1}{\omega_{p2}}+\frac{A_0}{\omega_{z}}}{A_0+1}s+1 \]

suppose \(\omega_{pA} \ll\omega_{pB}\), then \[ D(s) = \left( 1+ \frac{s}{\omega_{pA}}\right)\left( 1+ \frac{s}{\omega_{pB}}\right)\approx \frac{s^2}{\omega_{pA}\omega_{pB}}+\frac{s}{\omega_{pA}} + 1 \]

Thus, the two poles of the closed-loop transfer function of system are \[\begin{align} \omega_{pA} &= \frac{A_0+1}{\frac{1}{\omega_{p1}} + \frac{1}{\omega_{p2}}+\frac{A_0}{\omega_{z}}} = \frac{(A_0+1)\omega_{p1} \omega_{p2}}{\omega_{p1} + \omega_{p2} + \frac{A_0}{\omega_z}\omega_{p1} \omega_{p2}}\\ \omega_{pB} &= \omega_{p1} + \omega_{p2} + \frac{A_0}{\omega_z}\omega_{p1} \omega_{p2} \end{align}\]

non-dominant pole \(\omega_{p2}\) and zero \(\omega_z\) are in UGB

\[\begin{align} \omega_{pA} &\approx \omega_{p2}\\ \omega_{pB} &\approx (1+A_0)\omega_{p1} \end{align}\] Then, closed-loop transfer function is \[ H_{closed}(s) \approx \frac{\frac{A_0}{A_0+1}\left(1+\frac{s}{\omega_z}\right)}{\left(1+\frac{s}{(1+A_0)\omega_{p1}}\right)\left( 1+\frac{s}{\omega_{p2}} \right)} \]

Consider the Laplace transform function of step response, \(X(s)=\frac{1}{s}\) \[ Y(s)=\frac{1}{s}\times H_{closed}(s) \] Thus, the small-signal step response of the closed-loop amplifier is \[ y(t)=\frac{A_0}{A_0+1}\left[1-e^{-(A_0+1)\omega_{p1}t}-\left(1-\frac{\omega_{p2}}{\omega_z}\right)e^{-\omega_{p2}t} \right]u(t) \] Since, \(\omega_{p2}\ll (1+A_0)\omega_{p1}\). rewrite the \(y(t)\) \[ y(t)\approx \frac{A_0}{A_0+1}\left[1-\left(1-\frac{\omega_{p2}}{\omega_z}\right)e^{-\omega_{p2}t} \right]u(t) \]

perfect pole-zero cancellation with \(\omega_{p2}=\omega_z\) \[ y(t) \approx \frac{A_0}{A_0+1}\left[1-e^{-(A_0+1)\omega_{p1}t}\right]u(t) \approx \frac{A_0}{A_0+1}u(t) \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

clear
clc

A0 = 1e6;
wp1= 2*pi*1;   % 1Hz
wpz = 2*pi*2e4; % 20KHz

s=tf('s');

wp2 =0.5*wpz;
wz =2*wpz;
Ho = A0*(1+s/wz)/(1+s/wp1)/(1+s/wp2);
Hc = Ho/(1+Ho);


wi = logspace(-3, 7, 100000)*2*pi;
ti = linspace(0, 100,100000)*1e-6;

[mag_0p1, phase_0p1, wout_0p1] = bode(Ho, wi);
[vo_0p1, to_0p1] = step(Hc, ti);


wp2 =1*wpz;
wz =1*wpz;
Ho = A0*(1+s/wz)/(1+s/wp1)/(1+s/wp2);
Hc = Ho/(1+Ho);
[mag_1p0, phase_1p0, wout_1p0] = bode(Ho, wi);
[vo_1p0, to_1p0] = step(Hc, ti);


wp2 =2*wpz;
wz =0.5*wpz;
Ho = A0*(1+s/wz)/(1+s/wp1)/(1+s/wp2);
Hc = Ho/(1+Ho);
[mag_10p0, phase_10p0, wout_10p0] = bode(Ho, wi);
[vo_10p0, to_10p0] = step(Hc, ti);

subplot(2,2,1)
semilogx(wout_0p1(:)/2/pi, 20*log10(mag_0p1(:)),'b-',LineWidth=2);
hold on
semilogx(wout_1p0(:)/2/pi, 20*log10(mag_1p0(:)),'r-',LineWidth=2);
semilogx(wout_10p0(:)/2/pi, 20*log10(mag_10p0(:)),'g-',LineWidth=2);
grid on; xlabel('Hz'); ylabel('Mag (dB)');
legend('\omega_{p2}<\omega_{z}', '\omega_{p2}=\omega_{z}', '\omega_{p2}>\omega_{z}')

subplot(2,2,3)
semilogx(wout_0p1(:)/2/pi, phase_0p1(:),'b-',LineWidth=2);
hold on
semilogx(wout_1p0(:)/2/pi, phase_1p0(:),'r-',LineWidth=2);
semilogx(wout_10p0(:)/2/pi, phase_10p0(:),'g-',LineWidth=2);
grid on; xlabel('Hz'); ylabel('Phase')
legend('\omega_{p2}<\omega_{z}', '\omega_{p2}=\omega_{z}', '\omega_{p2}>\omega_{z}')

subplot(2,2,[2 4])
plot(to_0p1(:), vo_0p1(:),'b-',LineWidth=2);
hold on
plot(to_1p0(:), vo_1p0(:),'r-',LineWidth=2);
plot(to_10p0(:), vo_10p0(:),'g-',LineWidth=2);
grid on; xlabel('time'); ylabel('V')
legend('\omega_{p2}<\omega_{z}', '\omega_{p2}=\omega_{z}', '\omega_{p2}>\omega_{z}')

The zero comes from the mirror node

Thanks to unity gain buffer, zero is alleviated for \(C_c\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

A0 = 1e6;
wp1= 2*pi*1;   % 1Hz
wpz = 2*pi*2e4; % 20KHz
wp2 = 5*A0*wp1;

s=tf('s');

rio = 0.8;
wpx =rio*wpz;
wzx =wpz/rio;
wp1x = 1.5*wp1;   % keep UGB constant by changing dominant pole wp1x
Ho = A0*(1+s/wzx)/(1+s/wp1x)/(1+s/wp2)/(1+s/wpx);  % 2 poles + pole-zero doublet pair
Hc = Ho/(1+Ho);


wi = logspace(-3, 7, 100000)*2*pi;
ti = linspace(0, 100,100000)*1e-6;

[mag_0p1, phase_0p1, wout_0p1] = bode(Ho, wi);
[vo_0p1, to_0p1] = step(Hc, ti);


rio = 1;
wpx =rio*wpz;
wzx =wpz/rio;
wp1x = 1*wp1;
Ho = A0*(1+s/wzx)/(1+s/wp1x)/(1+s/wp2)/(1+s/wpx);
Hc = Ho/(1+Ho);
[mag_1p0, phase_1p0, wout_1p0] = bode(Ho, wi);
[vo_1p0, to_1p0] = step(Hc, ti);


rio = 1.25;
wpx =rio*wpz;
wzx =wpz/rio;
wp1x = 0.65*wp1;
Ho = A0*(1+s/wzx)/(1+s/wp1x)/(1+s/wp2)/(1+s/wpx);
Hc = Ho/(1+Ho);
[mag_10p0, phase_10p0, wout_10p0] = bode(Ho, wi);
[vo_10p0, to_10p0] = step(Hc, ti);

subplot(2,2,1)
semilogx(wout_0p1(:)/2/pi, 20*log10(mag_0p1(:)),'b-',LineWidth=2);
hold on
semilogx(wout_1p0(:)/2/pi, 20*log10(mag_1p0(:)),'r-',LineWidth=2);
semilogx(wout_10p0(:)/2/pi, 20*log10(mag_10p0(:)),'g-',LineWidth=2);
grid on; xlabel('Hz'); ylabel('Mag (dB)');
legend('\omega_{p2}<\omega_{z}', '\omega_{p2}=\omega_{z}', '\omega_{p2}>\omega_{z}')

subplot(2,2,3)
semilogx(wout_0p1(:)/2/pi, phase_0p1(:),'b-',LineWidth=2);
hold on
semilogx(wout_1p0(:)/2/pi, phase_1p0(:),'r-',LineWidth=2);
semilogx(wout_10p0(:)/2/pi, phase_10p0(:),'g-',LineWidth=2);
grid on; xlabel('Hz'); ylabel('Phase')
legend('\omega_{p2}<\omega_{z}', '\omega_{p2}=\omega_{z}', '\omega_{p2}>\omega_{z}')

subplot(2,2,[2 4])
plot(to_0p1(:), vo_0p1(:),'b-',LineWidth=2);
hold on
plot(to_1p0(:), vo_1p0(:),'r-',LineWidth=2);
plot(to_10p0(:), vo_10p0(:),'g-',LineWidth=2);
grid on; xlabel('time'); ylabel('V')
legend('\omega_{p2}<\omega_{z}', '\omega_{p2}=\omega_{z}', '\omega_{p2}>\omega_{z}')

divider doublet

Fundamentals of passive probe operation Active vs. passive probes [https://www.rohde-schwarz.com/us/products/test-and-measurement/essentials-test-equipment/rs-essentials-digital-oscilloscopes/understanding-passive-oscilloscope-probes_254518.html]

Secrets of the 10x Passive Probe Explained Understanding the internal design of a 10x passive probe reveals the trade-offs that affect signal accuracy, bandwidth, and noise performance. [https://www.teledynelecroy.com/oscilloscope/blog/secrets-of-the-10x-passive-probe-explained/]

TODO 📅

reference

Viola Schaffer, ISSCC 2021 Tutorials Designing Amplifiers for Stability [pdf]

J. H. Huijsing, "Operational Amplifiers, Theory and Design, 3rd ed. New York: Springer, 2017"

Razavi, Behzad. Design of Analog CMOS Integrated Circuits. India: McGraw-Hill, 2017. [pdf]

Sansen, Willy M. Analog Design Essentials. Germany: Springer US, 2006.

Gray, P. R., Hurst, P. J., Lewis, S. H., & Meyer, R. G. (2024). Analysis and design of analog integrated circuits (Sixth edition.). John Wiley & Sons, Inc..

Ahuja Compensation

B. K. Ahuja, "An Improved Frequency Compensation Technique for CMOS Operational Amplifiers," IEEE 1. Solid-State Circuits, vol. 18, no. 6, pp. 629-633, Dec. 1983. [https://sci-hub.se/10.1109/JSSC.1983.1052012]

U. Dasgupta, "Issues in "Ahuja" frequency compensation technique", IEEE International Symposium on Radio-Frequency Integration Technology, 2009. [https://sci-hub.se/10.1109/RFIT.2009.5383679]

R. J. Reay and G. T. A. Kovacs, "An unconditionally stable two-stage CMOS amplifier," in IEEE Journal of Solid-State Circuits, vol. 30, no. 5, pp. 591-594, May 1995 [https://sci-hub.se/10.1109/4.384174]

A. Garimella and P. M. Furth, "Frequency compensation techniques for op-amps and LDOs: A tutorial overview," 2011 IEEE 54th International Midwest Symposium on Circuits and Systems (MWSCAS), 2011 [https://sci-hub.se/10.1109/MWSCAS.2011.6026315]

H. Aminzadeh, R. Lotfi and S. Rahimian, "Design Guidelines for Two-Stage Cascode-Compensated Operational Amplifiers," 2006 13th IEEE International Conference on Electronics, Circuits and Systems, 2006 [https://sci-hub.se/10.1109/ICECS.2006.379776]

H. Aminzadeh and K. Mafinezhad, "On the power efficiency of cascode compensation over Miller compensation in two-stage operational amplifiers," Proceeding of the 13th international symposium on Low power electronics and design (ISLPED '08), Bangalore, India, 2008 [https://sci-hub.se/10.1145/1393921.1393995]

Stabilizing a 2-Stage Amplifier URL:https://a2d2ic.wordpress.com/2016/11/10/stabilizing-a-2-stage-amplifier/

EE 240B: Advanced Analog Circuit Design, Prof. Bernhard E. Boser [OTA II, Multi-Stage]

Parallel Compensation

R.Eschauzier "Wide Bandwidth Low Power Operational Amplifiers", Delft University Press, 1994.

Gene F. Franklin, J. David Powell, and Abbas Emami-Naeini. 2018. Feedback Control of Dynamic Systems (8th Edition) (8th. ed.). Pearson. 6.7 Compensation

Application Note AN-1286 Compensation for the LM3478 Boost Controller

ECEN 607 Advanced Analog Circuit Design Techniques Spring 2017 [Lect 1D Op-Amps Stability and Frequency Compensation Techniques]

Sergio Franco, San Francisco State University, Design with Operational Amplifiers and Analog Integrated Circuits, 4/e [pdf]

Pole-Zero Doublet

C. Mangelsdorf, "Don’t Fear the Doublet [Shop Talk: What You Didn’t Learn in School]," in IEEE Solid-State Circuits Magazine, vol. 18, no. 3, pp. 16-21, Summer 2026, doi: 10.1109/MSSC.2026.3707281.

Elad Alon, Lecture 10: Settling-Limited Amplifier Design Methodology, EE 240B – Spring 2018, Advanced Analog Integrated Circuits [https://inst.eecs.berkeley.edu/~ee240b/sp18/lectures/Lecture10_Settling_Design_2up.pdf]

Eric Chang, Prof. Elad Alon EE240B HW3 [https://inst.eecs.berkeley.edu/~ee240b/sp18/homeworks/hw3.pdf and https://inst.eecs.berkeley.edu/~ee240b/sp18/homeworks/hw3_soln.pdf]

Prof. Tai-Haur Kuo, Analog IC Design ( 類比積體電路設計 ), Operational Amplifiers http://msic.ee.ncku.edu.tw/course/aic/201809/chapter5.pdf

SERGIO FRANCO, Demystifying pole-zero doublets [https://www.edn.com/demystifying-pole-zero-doublets/]

B. Y. T. Kamath, R. G. Meyer and P. R. Gray, "Relationship between frequency response and settling time of operational amplifiers," in IEEE Journal of Solid-State Circuits, vol. 9, no. 6, pp. 347-352, Dec. 1974, [https://sci-hub.se/10.1109/JSSC.1974.1050527]

P. R. Gray and R. G. Meyer, "MOS operational amplifier design-a tutorial overview," in IEEE Journal of Solid-State Circuits, vol. 17, no. 6, pp. 969-982, Dec. 1982, [https://sci-hub.se/10.1109/JSSC.1982.1051851]

show qualitatively how changing pole locations in the s-plane affect impulse responses

natural frequency (\(\omega_n\), \(\omega_d\))

\(\omega_d\) called damped natural frequency \[ \omega_n^2 = \sigma^2 + \omega_d^2 \]

Underdamped step response (\(0<\zeta < 1\))

Critically damped step response (\(\zeta =1\))

Overdamped step response (\(\zeta >1\))

Complex-Conjugate Poles/Zeros

Section 6 Frequency Response Analysis [https://web.engr.oregonstate.edu/~webbky/ENGR203_files/Section%206%20Frequency%20Response%20Analysis.pdf]

maximally-flat or Butterworth response

Phase Margin & Damping Factor

• Phase Margin is defined for open loop system

• Damping Factor (\(\zeta\)) is defined for close loop system

We can analyze open loop system in a better perspective because it is simpler. So, we always use the loop gain analysis to find the phase margin and see whether the system is stable or not.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

zta = 0:.001:1;
PM = atan(2*zta ./ sqrt(sqrt(1+4*zta.^4) - 2*zta.^2))/pi*180;

[~, idx45] = min(abs(PM - 45));
[~, idx60] = min(abs(PM - 60));
[~, idx70] = min(abs(PM - 70));

plot(PM, zta, 'b',  LineWidth=3);
hold on
plot(PM(idx45), zta(idx45), 'ro', MarkerFaceColor='r', LineWidth=3, MarkerSize=8)
text(PM(idx45)+2, zta(idx45), ['\zeta=' num2str(zta(idx45)) ' @PM=45^o'])
plot(PM(idx60), zta(idx60), 'ro', MarkerFaceColor='r', LineWidth=3, MarkerSize=8)
text(PM(idx60)+2, zta(idx60), ['\zeta=' num2str(zta(idx60)) ' @PM=60^o'])
plot(PM(idx70), zta(idx70), 'ro', MarkerFaceColor='r', LineWidth=3, MarkerSize=8)
text(PM(idx70)-10, zta(idx70), ['\zeta=' num2str(zta(idx70)) ' @PM=70^o'])
grid on; xlabel('Phase Margin, ^o'); ylabel('Damping ratio, \zeta')

Zeros & Non-Minimum Phase Zeros

Influence of Zeros and Non-Minimum Phase Zeros of Transfer Functions on Dynamical System Behavior [https://aleksandarhaber.com/effect-of-zeros-of-transfer-functions-on-dynamical-system-behavior/]

The zeros in the right half of the complex plane are called nonminimum phase zeros. Systems with nonminimum phase zeros are called nonminimum phase systems

Zero close to the real pole attenuates the effect of that pole on the system response

Zeros Tend to Increase the Overshoot of the System

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

zeta=0.4
omega_n=3
k=1
s=tf('s')

W1=1/(s^2+2*zeta*s+1)
W2=(1/(k*zeta))*s*W1
W3=W1+W2

figure(1)
hold on
step(W1,'r')
step(W2,'k')
step(W3,'b')
grid

Nonminimum Phase Zeros – Effect on the Transient Response

1
2
3
4
5
6
7
8
9
10
11
12
13

zeta=0.4
omega_n=3
k=1
s=tf('s')
S1=1/(s^2+2*zeta*s+1)
S2=(1/(k*zeta))*s*S1
S=S1-S2
figure(1)
hold on
step(S1,'r')
step(-S2,'k')
step(S,'b')
grid

\[\begin{align} TF &= \frac{s +\omega_z}{s^2+2\zeta \omega_ns+\omega_n^2} \\ &= \frac{\omega _z}{\omega _n^2}\cdot \frac{1+s/\omega _z}{1+s^2/\omega_n^2+2\zeta s/\omega_n} \end{align}\]

Let \(s=j\omega\) and omit factor, \[ A_\text{dB}(\omega) = 10\log[1+(\frac{\omega}{\omega _z})^2] - 10\log[1+\frac{\omega^4}{\omega_n^4}+\frac{2\omega^2(2\zeta ^2 -1)}{\omega_n^2}] \] peaking frequency \(\omega_\text{peak}\) can be obtained via \(\frac{\mathrm{d} A_\text{dB}(\omega)}{\mathrm{d}\omega} = 0\) \[ \omega_\text{peak} = \omega_z \sqrt{\sqrt{(\frac{\omega_n}{\omega_z})^4 - 2(\frac{\omega_n}{\omega_z})^2(2\zeta ^2-1)+1} - 1} \]

minimum-phase system vs Non-minimum phase system

• a linear, time-invariant system is said to be minimum-phase if the system and its inverse are causal and stable

• Systems that are causal and stable whose inverses are causal and unstable are known as non-minimum-phase systems

Settling Time

One Pole

we have \[ \tau \approx \left(1 + \frac{R_1}{R_2}\right)\frac{1}{A_0\omega_0}= \frac{1}{\beta \omega_\text{ugb}} \]

Two Poles

with open-loop transfer function \(A_{OL}=\frac{A_0}{(1+s/\omega_1)(1+s/\omega_2)}\) and assuming \(\omega_1\) is dominant pole, then yield closed-loop transfer function

\[\begin{align} A_{CL}(s) &= \frac{\frac{A_0}{(1+s/\omega_1)(1+s/\omega_2)}}{1+\beta \frac{A_0} {(1+s/\omega_1)(1+s/\omega_2)}} \\ &= \frac{A_0}{1+A_0 \beta}\frac{1}{\frac{s^2}{\omega_1\omega_2(1+A_0\beta)}+\frac{1/\omega_1+1/\omega_2}{1+A_0\beta}s+1} \\ &\approx \frac{A_0}{1+A_0 \beta}\frac{1}{\frac{s^2}{\omega_u\omega_2}+\frac{1}{\omega_u}s+1} \\ &= \frac{A_0}{1+A_0 \beta}\frac{\omega_u\omega_2}{s^2+\omega_2s+\omega_u\omega_2} \end{align}\]

That is \(\omega_n = \sqrt{\omega_u\omega_2}\), \(\zeta = \frac{1}{2}\sqrt{\frac{\omega_2}{\omega_u}}\) , where \(\omega_u\approx \beta A_0 \omega_1\) is the unity gain bandwidth

Rise Time (0% to 100% )

\[ t_r = \frac{\pi - \beta}{\omega_d}=\frac{\pi - \arctan\frac{\omega_n\sqrt{1-\zeta^2}}{\zeta\omega_n}}{\omega_n\sqrt{1-\zeta^2}}\approx\frac{\pi - \arctan\frac{\sqrt{1-\zeta^2}}{\zeta}}{\sqrt{\omega_u\omega_2}\sqrt{1-\zeta^2}}=\frac{\pi - \arctan\frac{\sqrt{1-\zeta^2}}{\zeta}}{\omega_u\sqrt{k(1-\zeta^2)}} \] where \(k = \frac{\omega_2}{\omega_u}\), is the function of PM

1
2
3
4

PM = 70;
ztap = 0.80;
k = 1/tan((90-PM)/180*pi)
tr = (pi - atan(sqrt(1-ztap^2)/ztap))/sqrt(k*(1-ztap^2))

Settling Time

Gene F. Franklin, Feedback Control of Dynamic Systems, 8th Edition

As we know \[ \zeta \omega_n=\frac{1}{2}\sqrt{\frac{\omega_2}{\omega_u}}\cdot \sqrt{\omega_u\omega_2}=\frac{1}{2}\omega_2 \]

Then \[ t_s = \frac{9.2}{\omega_2} \]

For \(\text{PM}=70^o\), \(\omega_2 = 2.75\omega_u\), that is \[ t_s \approx \frac{3.35}{\omega_u} \]

For \(\text{PM}=45^o\), \(\omega_2 = \omega_u\), that is \[ t_s \approx \frac{9.2}{\omega_u} \]

Above equation is valid only for underdamped, \(\zeta=\frac{1}{2}\sqrt{\frac{\omega_2}{\omega_u}}\lt 1\), that is \(\omega_2\lt 4\omega_u\)

2 Stage RC filter

High Pass Filter

Since \(1/sC_1+R_1 \gg R_0\) \[ \frac{V_m}{V_i}(s) \approx \frac{R_0}{R_0 + 1/sC_0} = \frac{sR_0C_0}{1+sR_0C_0} \] step response of \(V_m\) \[ V_m(t) = e^{-t/R_0C_0} \] where \(\tau = R_0C_0\)

And \(V_o(s)\) can be expressed as \[\begin{align} \frac{V_o}{V_i}(s) & \approx \frac{sR_0C_0}{1+sR_0C_0} \cdot \frac{sR_1C_1}{1+sR_1C_1} \\ &= \frac{sR_0C_0R_1C_1}{R_0C_0-R_1C_1}\left(\frac{1}{1+sR_1C_1} - \frac{1}{1+sR_0C_0}\right) \end{align}\]

Then step response of \(Vo\) \[\begin{align} Vo(t) &= \frac{R_0C_0R_1C_1}{R_0C_0-R_1C_1} \left(\frac{1}{R_1C_1}e^{-t/R_1C_1} - \frac{1}{R_0C_0}e^{-t/R_0C_0}\right) \\ &= \frac{1}{R_0C_0-R_1C_1}\left(R_0C_0e^{-t/R_1C_1} - R_1C_1e^{-t/R_0C_0}\right) \\ &\approx \frac{1}{R_0C_0-R_1C_1}\left(R_0C_0e^{-t/R_1C_1} - R_1C_1\right) \end{align}\]

where \(\tau=R_1C_1\)

Partial-fraction Expansion

1
2
3
4
5
6
7
8
9
10

syms C0
syms R0
syms C1
syms R1
syms s

Z0 = 1/s/C1 + R1;
Z1 = R0*Z0/(R0+Z0);
vm = Z1 / (Z1 + 1/s/C0);
vo = R1/Z0 * vm;

1
2
3
4
5
6
7
8
9
10
11

>> partfrac(vm, s)

ans =

1 - (s*(C1*R0 + C1*R1) + 1)/(C0*C1*R0*R1*s^2 + (C0*R0 + C1*R0 + C1*R1)*s + 1)

>> partfrac(vo, s)

ans =

1 - (s*(C0*R0 + C1*R0 + C1*R1) + 1)/(C0*C1*R0*R1*s^2 + (C0*R0 + C1*R0 + C1*R1)*s + 1)

\[\begin{align} V_m(s) &= 1 - \frac{s(C_1R_0+C_1R_1)+1}{C_0C_1R_0R_1s^2+(C_0R_0+C_1R_0+C_1R_1)s+1} \\ V_o(s) &= 1 - \frac{s(C_0R_0+C_1R_0+C_1R_1)+1}{C_0C_1R_0R_1s^2+(C_0R_0+C_1R_0+C_1R_1)s+1} \end{align}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

C0 = 200e-9;
R0 = 50;
C1 = 400e-15;
R1 = 200e3;

s = tf("s");

Z0 = 1/s/C1 + R1;
Z1 = R0*Z0/(R0+Z0);
vm = Z1 / (Z1 + 1/s/C0);
vo = R1/Z0 * vm;

vm_exp = 1 - (s*(C1*R0 + C1*R1) + 1)/(C0*C1*R0*R1*s^2 + (C0*R0 + C1*R0 + C1*R1)*s + 1);
vo_exp = 1 - (s*(C0*R0 + C1*R0 + C1*R1) + 1)/(C0*C1*R0*R1*s^2 + (C0*R0 + C1*R0 + C1*R1)*s + 1);

figure(1)
subplot(1,2,1)
step(vm, 500e-9, 'k-o');
hold on;
step(vm_exp, 500e-9, 'r-^')
title('vm step response')
grid on;
legend()


subplot(1,2,2)
step(vo, 500e-9, 'k-o');
hold on;
step(vo_exp, 500e-9, 'r-^')
title('vo step response')
grid on;
legend()


% with approximation
figure(2)
vm_exp2 = s*R0*C0/(1+s*R0*C0);
vo_exp2 = s*R0*C0/(1+s*R0*C0) * s*R1*C1/(1+s*R1*C1);

subplot(1,2,1)
step(vm, 500e-9, 'k-o');
hold on;
step(vm_exp2, 500e-9, 'r-^')
title('vm step response')
grid on;
legend()

subplot(1,2,2)
step(vo, 500e-9, 'k-o');
hold on;
step(vo_exp2, 500e-9, 'r-^')
title('vo step response')
grid on;
legend()

spectre vs matlab

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

C0 = 200e-9;
R0 = 50;
C1 = 400e-15;
R1 = 200e3;

s = tf("s");

Z0 = 1/s/C1 + R1;
Z1 = R0*Z0/(R0+Z0);
vm = Z1 / (Z1 + 1/s/C0);
vo = R1/Z0 * vm;

step(vm, 500e-9);
hold on;
step(vo, 500e-9);

grid on

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

>> vm

vm =

          1.024e-44 s^5 + 2.56e-37 s^4 + 1.6e-30 s^3
  -----------------------------------------------------------
  1.024e-44 s^5 + 2.571e-37 s^4 + 1.626e-30 s^3 + 1.6e-25 s^2

Continuous-time transfer function.

>> vo

vo =

                 8.194e-52 s^6 + 2.048e-44 s^5 + 1.28e-37 s^4
  ---------------------------------------------------------------------------
  8.194e-52 s^6 + 3.081e-44 s^5 + 3.871e-37 s^4 + 1.638e-30 s^3 + 1.6e-25 s^2

Continuous-time transfer function.

Low Pass Filter

\[ \left\{ \begin{array}{cl} \frac{V_i - V_m}{R_0} &= C_0\frac{\mathrm{d}V_m}{\mathrm{d}t} + C_1\frac{\mathrm{d}V_o}{\mathrm{d}t} \\ \frac{V_m - V_o}{R_1} &= C_1\frac{\mathrm{d}V_o}{\mathrm{d}t} \\ V_m(t=0) &= 1 \\ V_o(t=0) &= 0 \end{array} \right. \]

Take into initial condition account \[ \frac{\mathrm{d}V_m}{\mathrm{d}t} \overset{\mathcal{L}}{\longrightarrow} sV_M-V_{m0} \] where \(V_{m0} = 1\)

\[\begin{align} V_O(s) &= \frac{V_I}{s^2R_0C_0R_1C_1+s(R_0C_0+R_1C_1+R_0C_1)+1} + \frac{V_{m0}R_0C_0}{s^2R_0C_0R_1C_1+s(R_0C_0+R_1C_1+R_0C_1)+1} \\ &\approx \frac{V_I}{s^2R_0C_0R_1C_1+sR_0(C_0+C_1)+1} + \frac{V_{m0}R_0C_0}{s^2R_0C_0R_1C_1+sR_0(C_0+C_1)+1} \\ &= \frac{V_I}{R_0(C_0+C_1)}\left(\frac{R_0(C_0+C_1)}{sR_0(C_0+C_1)+1} - \frac{R_1\frac{C_0C_1}{C_0+C_1}}{sR_1\frac{C_0C_1}{C_0+C_1}+1}\right) \\ &+ \frac{C_0}{C_0+C_1}\left(\frac{R_0(C_0+C_1)}{sR_0(C_0+C_1)+1} - \frac{R_1\frac{C_0C_1}{C_0+C_1}}{sR_1\frac{C_0C_1}{C_0+C_1}+1}\right) \end{align}\]

with \(V_I = \frac{1}{s}\), using inverse Laplace transform \[\begin{align} V_o(t) &= 1 - \frac{C_1}{C_0+C_1}e^{-t/\tau_0}-\frac{C_0}{C_0+C_1}e^{-t/\tau_1} - \frac{R_1C_0C_1}{R_0(C_0+C_1)^2} \tag{Eq.0} \\ &= 1 - \frac{C_1}{C_0+C_1}e^{-t/\tau_0}-\frac{C_0}{C_0+C_1}e^{-t/\tau_1} \tag{Eq.1} \end{align}\]

where

\[\begin{align} \tau_0 &= R_0(C_0+C_1) \\ \tau_1 &= R_1C_1\cdot \frac{C_0}{C_0+C_1} \end{align}\]

and \(\tau_0 \gg \tau_1\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

R0 = 100e3;
C0 = 200e-15;
R1 = 10e3;
C1 = 100e-15;

s = tf('s');

VI = 1/s;
Vm0 = 1;

deno = (s^2*R0*C0*R1*C1 + s*(R0*C0 + R1*C1 + R0*C1) + 1);
VO = VI/deno + (Vm0*R0*C0)/deno;
VM = (1+s*R1*C1)*VO;

t = linspace(0,40,1e3);  % ns
[vot, ~] = impulse(VO, t*1e-9);
[vmt, ~] = impulse(VM, t*1e-9);

tau0 = R0*(C0+C1)*1e9; %ns
tau1 = R1*C0*C1/(C0+C1)*1e9; %ns
y0 = 1 - C1/(C0+C1)*exp(-t/tau0) - C0/(C0+C1)*exp(-t/tau1) - R1*C0*C1/R0/(C0+C1)^2;  % Eq.0
y1 = 1 - C1/(C0+C1)*exp(-t/tau0) - C0/(C0+C1)*exp(-t/tau1);  % Eq.1

plot(t, vot, t, vmt,LineWidth=2);
hold on
plot(t,y0, t,y1, LineWidth=2, LineStyle="--" );
xlim([-10, 40])
legend('V_o(t)', 'V_m(t)','y_0(t)', 'y_1(t)', fontsize=12)
xlabel('t (ns)')
ylabel('mag (V)')
grid on;

reference

Gene F. Franklin, J. David Powell, and Abbas Emami-Naeini. 2018. Feedback Control of Dynamic Systems (8th Edition) (8th. ed.). Pearson. [pdf]

Katsuhiko Ogata, Modern Control Engineering, 5th edition [pdf]

C. T. Chuang, "Analysis of the settling behavior of an operational amplifier," in IEEE Journal of Solid-State Circuits, vol. 17, no. 1, pp. 74-80, Feb. 1982 [https://sci-hub.se/10.1109/JSSC.1982.1051689]

Jason Sachs, Second-Order Systems, Part I: Boing!! [https://www.embeddedrelated.com/showarticle/671.php]

Are AC-Driven Circuits Linear?

\[ f(x_1 + x_2)= f(x_1)+ f(x_2) \]

Often, AC-driven circuits can be mistaken as non-linear as the basis that determines the linearity of a circuit is the relationship between the voltage and current.

While an AC signal varies with time, it still exhibits a linear relationship across elements like resistors, capacitors, and inductors. Therefore, AC driven circuits are linear.

Phasor

Phasor concept has no real physical significance. It is just a convenient mathematical tool.

Phasor analysis determines the steady-state response to a linear circuit driven by sinusoidal sources with frequency \(f\)

If your circuit includes transistors or other nonlinear components, all is not lost. There is an extension of phasor analysis to nonlinear circuits called small-signal analysis in which you linearize the components before performing phasor analysis - AC analyses of SPICE

A sinusoid is characterized by 3 numbers, its amplitude, its phase, and its frequency. For example \[ v(t) = A\cos(\omega t + \phi) \tag{1} \] In a circuit there will be many signals but in the case of phasor analysis they will all have the same frequency. For this reason, the signals are characterized using only their amplitude and phase.

The combination of an amplitude and phase to describe a signal is the phasor for that signal.

Thus, the phasor for the signal in \((1)\) is \(A\angle \phi\)

In general, phasors are functions of frequency

Often it is preferable to represent a phasor using complex numbers rather than using amplitude and phase. In this case we represent the signal as: \[ v(t) = \Re\{Ve^{j\omega t} \} \tag{2} \] where \(V=Ae^{j\phi}\) is the phasor.

\((1)\) and \((2)\) are the same

Phasor Model of a Resistor

A linear resistor is defined by the equation \(v = Ri\)

Now, assume that the resistor current is described with the phasor \(I\). Then \[ i(t) = \Re\{Ie^{j\omega t}\} \] \(R\) is a real constant, and so the voltage can be computed to be \[ v(t) = R\Re\{Ie^{j\omega t}\} = \Re\{RIe^{j\omega t}\} = \Re\{Ve^{j\omega t}\} \] where \(V\) is the phasor representation for \(v\), i.e. \[ V = RI \]

1. Thus, given the phasor for the current we can directly compute the phasor for the voltage across the resistor.

2. Similarly, given the phasor for the voltage across a resistor we can compute the phasor for the current through the resistor using \(I = \frac{V}{R}\)

Phasor Model of a Capacitor

A linear capacitor is defined by the equation \(i=C\frac{\mathrm{d}v}{\mathrm{d}t}\)

Now, assume that the voltage across the capacitor is described with the phasor \(V\). Then \[ v(t) = \Re\{ V e^{j\omega t}\} \] \(C\) is a real constant \[ i(t) = C\Re\{\frac{\mathrm{d}}{\mathrm{d}t}V e^{j\omega t}\} = \Re\{j\omega C V e^{j\omega t}\} \] The phasor representation for \(i\) is \(i(t) = \Re\{Ie^{j\omega t}\}\), that is \(I = j\omega C V\)

1. Thus, given the phasor for the voltage across a capacitor we can directly compute the phasor for the current through the capacitor.

2. Similarly, given the phasor for the current through a capacitor we can compute the phasor for the voltage across the capacitor using \(V=\frac{I}{j\omega C}\)

Phasor Model of an Inductor

A linear inductor is defined by the equation \(v=L\frac{\mathrm{d}i}{\mathrm{d}t}\)

Now, assume that the inductor current is described with the phasor \(I\). Then \[ i(t) = \Re\{ I e^{j\omega t}\} \] \(L\) is a real constant, and so the voltage can be computed to be \[ v(t) = L\Re\{\frac{\mathrm{d}}{\mathrm{d}t}I e^{j\omega t}\} = \Re\{j\omega L I e^{j\omega t}\} \] The phasor representation for \(v\) is \(v(t) = \Re\{Ve^{j\omega t}\}\), that is \(V = j\omega L I\)

1. Thus, given the phasor for the current we can directly compute the phasor for the voltage across the inductor.

2. Similarly, given the phasor for the voltage across an inductor we can compute the phasor for the current through the inductor using \(I=\frac{V}{j\omega L}\)

Impedance and Admittance

Impedance and admittance are generalizations of resistance and conductance.

They differ from resistance and conductance in that they are complex and they vary with frequency.

Impedance is defined to be the ratio of the phasor for the voltage across the component and the current through the component: \[ Z = \frac{V}{I} \]

Impedance is a complex value. The real part of the impedance is referred to as the resistance and the imaginary part is referred to as the reactance

For a linear component, admittance is defined to be the ratio of the phasor for the current through the component and the voltage across the component: \[ Y = \frac{I}{V} \]

Admittance is a complex value. The real part of the admittance is referred to as the conductance and the imaginary part is referred to as the susceptance.

Response to Complex Exponentials

The response of an LTI system to a complex exponential input is the same complex exponential with only a change in amplitude

\[\begin{align} y(t) &= H(s)e^{st} \\ H(s) &= \int_{-\infty}^{+\infty}h(\tau)e^{-s\tau}d\tau \end{align}\]

where \(h(t)\) is the impulse response of a continuous-time LTI system

convolution integral is used here

\[\begin{align} y[n] &= H(z)z^n \\ H(z) &= \sum_{k=-\infty}^{+\infty}h[k]z^{-k} \end{align}\]

where \(h(n)\) is the impulse response of a discrete-time LTI system

convolution sum is used here

The signals of the form \(e^{st}\) in continuous time and \(z^{n}\) in discrete time, where \(s\) and \(z\) are complex numbers are referred to as an eigenfunction of the system, and the amplitude factor \(H(s)\), \(H(z)\) is referred to as the system's eigenvalue

Laplace transform

One of the important applications of the Laplace transform is in the analysis and characterization of LTI systems, which stems directly from the convolution property \[ Y(s) = H(s)X(s) \] where \(X(s)\), \(Y(s)\), and \(H(s)\) are the Laplace transforms of the input, output, and impulse response of the system, respectively

From the response of LTI systems to complex exponentials, if the input to an LTI system is \(x(t) = e^{st}\), with \(s\) the ROC of \(H(s)\), then the output will be \(y(t)=H(s)e^{st}\); i.e., \(e^{st}\) is an eigenfunction of the system with eigenvalue equal to the Laplace transform of the impulse response.

s-Domain Element Models

Sinusoidal Steady-State Analysis

Here Sinusoidal means that source excitations have the form \(V_s\cos(\omega t +\theta)\) or \(V_s\sin(\omega t+\theta)\)

Steady state mean that all transient behavior of the stable circuit has died out, i.e., decayed to zero

\(s\)-domain and phasor-domain

Phasor analysis is a technique to find the steady-state response when the system input is a sinusoid. That is, phasor analysis is sinusoidal analysis.

• Phasor analysis is a powerful technique with which to find the steady-state portion of the complete response.
• Phasor analysis does not find the transient response.
• Phasor analysis does not find the complete response.

The beauty of the phasor-domain circuit is that it is described by algebraic KVL and KCL equations with time-invariant sources, not differential equations of time

The difference here is that Laplace analysis can also give us the transient response

General Response Classifications

• zero-input response, zero-state response & complete response

  

  The zero-state response is given by \(\mathscr{L^1}[H(s)F(s)]\), for the arbitrary \(s\)-domain input \(F(s)\)

  where \(Z_L(s) = sL\), the inductor with zero initial current \(i_L(0)=0\) and \(Z_C(s)=1/sC\) with zero initial voltage \(v_C(0)=0\)

• transient response & steady-state response

  

• natural response & forced response

  

Transfer Functions and Frequency Response

transfer function

The transfer function \(H(s)\) is the ratio of the Laplace transform of the output of the system to its input assuming all zero initial conditions.

frequency response

An immediate consequence of convolution is that an input of the form \(e^{st}\) results in an output \[ y(t) = H(s)e^{st} \] where the specific constant \(s\) may be complex, expressed as \(s = \sigma + j\omega\)

A very common way to use the exponential response of LTIs is in finding the frequency response i.e. response to a sinusoid

First, we express the sinusoid as a sum of two exponential expressions (Euler’s relation): \[ \cos(\omega t) = \frac{1}{2}(e^{j\omega t}+e^{-j\omega t}) \] If we let \(s=j\omega\), then \(H(-j\omega)=H^*(j\omega)\), in polar form \(H(j\omega)=Me^{j\phi}\) and \(H(-j\omega)=Me^{-j\phi}\). \[\begin{align} y_+(t) & = H(s)e^{st}|_{s=j\omega} = H(j\omega)e^{j\omega t} = M e^{j(\omega t + \phi)} \\ y_-(t) & = H(s)e^{st}|_{s=-j\omega} = H(-j\omega)e^{-j\omega t} = M e^{-j(\omega t + \phi)} \end{align}\]

By superposition, the response to the sum of these two exponentials, which make up the cosine signal, is the sum of the responses \[\begin{align} y(t) &= \frac{1}{2}[H(j\omega)e^{j\omega t} + H(-j\omega)e^{-j\omega t}] \\ &= \frac{M}{2}[e^{j(\omega t + \phi)} + e^{-j(\omega t + \phi)}] \\ &= M\cos(\omega t + \phi) \end{align}\]

where \(M = |H(j\omega|\) and \(\phi = \angle H(j\omega)\)

This means if a system represented by the transfer function \(H(s)\) has a sinusoidal input, the output will be sinusoidal at the same frequency with magnitude \(M\) and will be shifted in phase by the angle \(\phi\)

Laplace transform vs. Fourier transform

• Laplace transforms such as \(Y(s)=H(s)U(s)\) can be used to study the complete response characteristics of systems, including the transient response—that is, the time response to an initial condition or suddenly applied signal
• This is in contrast to the use of Fourier transforms, which only take into account the steady-state response

Given a general linear system with transfer function \(H(s)\) and an input signal \(u(t)\), the procedure for determining \(y(t)\) using the Laplace transform is given by the following steps:

Laplace derivative formula at \(t = 0\)

S. Boyd EE102 Table of Laplace Transforms. [https://web.stanford.edu/~boyd/ee102/laplace-table.pdf]

One-Sided (unilateral) and Two-Sided (bilateral) Laplace Transforms

[https://sps.ewi.tudelft.nl/Education/courses/ee2s11/slides/3_laplace_P.pdf]

reference

Ken Kundert. Introduction to Phasors. Designer’s Guide Community. September 2011.

How to Perform Linearity Circuit Analysis [https://resources.pcb.cadence.com/blog/2021-how-to-perform-linearity-circuit-analysis]

Stephen P. Boyd. EE102 Lecture 7 Circuit analysis via Laplace transform [https://web.stanford.edu/~boyd/ee102/laplace_ckts.pdf]

Cheng-Kok Koh, EE695K VLSI Interconnect, S-Domain Analysis [https://engineering.purdue.edu/~chengkok/ee695K/lec3c.pdf]

Kenneth R. Demarest, Circuit Analysis using Phasors, Laplace Transforms, and Network Functions [https://people.eecs.ku.edu/~demarest/212/Phasor%20and%20Laplace%20review.pdf]

DeCarlo, R. A., & Lin, P.-M. (2009). Linear circuit analysis : time domain, phasor, and Laplace transform approaches (3rd ed).

Davis, Artice M.. "Linear Circuit Analysis." The Electrical Engineering Handbook - Six Volume Set (1998)

Duane Marcy, Fundamentals of Linear Systems [http://lcs-vc-marcy.syr.edu:8080/Chapter22.html]

Gene F. Franklin, J. David Powell, and Abbas Emami-Naeini. 2018. Feedback Control of Dynamic Systems (8th Edition) (8th. ed.). Pearson.

Data Register, DR:

• Bypass Register, BR
• Boundary Scan Register, BSR

Instruction Register, IR

TAP Controller

• FSM and Shift Register of DR and IR works at the posedge of the clock
• TMS, TDI, TDO and Hold Register of DR and IR changes value at the negedge of the clock

capture IR 01, the fixed is for easier fault detection

After power-up, they may not be in sync, but there is a trick. Look at the state machine and notice that no matter what state you are, if TMS stays at "1" for five clocks, a TAP controller goes back to the state "Test-Logic Reset". That's used to synchronize the TAP controllers.

It is important to note that in a typical Boundary-Scan test, the time between launching a signal from driver (at the falling edge of test clock (TCK) in the Update-DR or Update-IR TAP Controller state) and capturing that signal (at the rising edge of TCK in the Caputre-DR TAP Controller state) is no less tha 2.5 TCK cycles

Further, the time between successive launches on a driver is governed - not only by the TCk rate - but by the amount of serial data shifting needed to load the next pattern data in the concatenated Boundary-Scan Registers of the Boundary-Scan chain

Thus the effective test data rate of a driver could be thousands of the times lower than the TCK rate

1. For DC-coupled interconnect, this time is of no concern
2. For AC-coupled interconnect, the signal may easily decay partially or completely before it can be captured
3. If only partial decay occurs before capture, that decay will very likely be completed before the driver produces the next edge

AC-coupling

In general, AC-coupling can distort a signal transmitted across a channel depending on its frequency.

Figure 5

• The high frequency signal is relatively unaffected by the coupling
• The low frequency signal is severely impacted
  1. it decays to \(V_T\) after a few time constants
  2. its amplitude is double the input amplitude > transient response, before AC-coupling capacitor: \(-A_p \to A_p\); after AC-coupling capacitor \(V_T \to V_T+2A_p\) > A key item to note is that the transitions in the original signal are preserved, although their start and end points are offset > > compared to where they were in the high frequency

Test signal implementation

The test data is either the content of the Boundary-Scan Register Update latch (U) when executing the (DC) EXTEST instruction, or an "AC Signal" when an AC testing instruction is loaded into the device.

The AC signal is a test waveform suited for transmission through AC-coupling

Test signal reception

• When an AC testing instruction is loaded, a specialized test receiver detects transitoins of the AC signal seen at the input and determines if this represents a logic '0' or '1'
• When EXTEST is loaded, the input signal level is detected and sent to the output of the test receiver to the Boundary-Scan Register cell

When testing for a shorted capacitor, the test software must ensure that enough time has passed for the signal to decay before entering Capture-DR, either by stopping TCk or by spending additional TCK cycles in the Run-Test/Idle TAP Controller state

EXTEST_PULSE & EXTEST_TRAIN

The two new AC-test instructions provided by this standard differ primarily in the number and timing of transitions to provide flexibility in dealing with the specific dynamic behavior of the channels being tested

AC Test Signal essentially modulates test data so that it will propagate through AC-coupled channels, for devices that contatin AC pins

Tools should use the EXTEST_PULSE instruction unless there is a specific requirement for the EXTEST_TRAIN instruction

EXTEST_PULSE

Generate two additional driver transitions and allows a tester to vary the time between them dependent on how many TCK cycles the TAP is left in the Run-Test/Idle TAP Controller state.

This is intended to allow any undesired transient condition to decay to a DC steady-state value when that will make the final transition more reliably detectable

The duration in the Run-Test/Idle TAP Controller state should be at least three times the high-pass coupling time constant. This allows the first additional transition to decay away to the DC steady-state value for the channel, and ensures that the full amplitude of the final transition is added to or subtracted from that steady-state value

This establishes a known initial condition for the final transition and permits reliable specification of the detection threshold of the test receiver

EXTEST_TRAIN

Generate multiple additional transitions, the number dependent on how long the TAP is left in the Run-Test/Idle TAP Controller state

This is intended to allow any undesired transient condition to decay to an AC steady-state value when that will make the final transition more reliably detectable

IEEE Std 1149.6-2003

This standard is built on top of IEEE Std 1149.1 using the same Test Access Port structure and Boundary-Scan architecture.

• It adds the concept of a "test receiver" to input pins that are expected to handle differential and/or AC-coupling
• It adds two new instructions that cause drivers to emit AC waveforms that are processed by test receivers.

JTAG Instruction

Implementation

• AC mode hysteresis, detect transistion
• DC mode threshold is determined by jtag initial value

reference

IEEE Std 1149.1-2001, IEEE Standard Test Access Port and Boundary-Scan Architecture, IEEE, 2001

IEEE Std 1149.6-2003, IEEE Standard for BoundaryScan Testing of Advanced Digital Networks, IEEE, 2003

IEEE 1149.6 Tutorial | Testing AC-coupled and Differential High-speed Nets [https://www.asset-intertech.com/resources/eresources/ieee-11496-tutorial-testing-ac-coupled-and-differential-high-speed-nets/]

Prof. James Chien-Mo Li, Lab of Dependable Systems, National Taiwan University. VLSI Testing [http://cc.ee.ntu.edu.tw/~cmli/VLSItesting/]

K.P. Parker, The Boundary Scan Handbook, 3rd ed., Kluwer Academic, 2003.

B. Eklow, K. P. Parker and C. F. Barnhart, "IEEE 1149.6: a boundary-scan standard for advanced digital networks," in IEEE Design & Test of Computers, vol. 20, no. 5, pp. 76-83, Sept.-Oct. 2003, doi: 10.1109/MDT.2003.1232259.

autocorrelation

The expectation returns the probability-weighted average of the specific function at that specific time over all possible realizations of the process

Derivatives of Random Processes

since \(x(t)\) is stationary process, and \(y(t) = \frac{\mathrm{d}x(t)}{\mathrm{d}t}\)

Using \(R_{yy}(\tau) = h(\tau)*R_{xx}(\tau)*h(-\tau)\)

\[\begin{align} R_{yy}(\tau) &= \mathcal{F}^{-1}[H(j\omega)\Phi_{xx}(j\omega)H(-j\omega)] \\ &= \mathcal{F}^{-1}[-(j\omega)^2\Phi_{xx}(j\omega)] \end{align}\]

we obtain the autocorrelation function of the output process as \[ R_{yy}(\tau) = -\frac{\mathrm{d}^2}{\mathrm{d}\tau^2}R_{xx}(\tau) \]

Liu Congfeng, Xidian University. Random Signal Processing: Chapter 5 Linear System: Random Process [https://web.xidian.edu.cn/cfliu/files/20121125_153218.pdf]

[https://sharif.ir/~bahram/sp4cl/PapoulisLectureSlides/lectr14.pdf]

autocorrelation of a complex process

Start from the definition of the (ensemble) autocorrelation of a complex process: \[ R_n(\tau) = \big\langle\, n(t+\tau)\,\overline{n(t)}\,\big\rangle, \] where \(\langle\cdot\rangle\) averages over the random phases. Substituting \(n(t) = \sum_i N[i]e^{ji\omega_0 t}\) gives a double sum: \[ R_n(\tau) = \sum_i \sum_k \big\langle N[i]\,\overline{N[k]}\big\rangle\, e^{j(i-k)\omega_0 t}\, e^{ji\omega_0 \tau}. \] Everything hinges on the correlation matrix \(\langle N[i]\overline{N[k]}\rangle\), and there are two cases.

Ergodicity

ensemble autocorrelation and temporal autocorrelation (time autocorrelation)

ECE438 - Laboratory 7: Discrete-Time Random Processes (Week 2) October 6, 2010 [https://engineering.purdue.edu/VISE/ee438L/lab7/pdf/lab7b.pdf]

Ensemble Averages & Time Averages

[https://ece-research.unm.edu/bsanthan/ece541/stat.pdf]

[https://www.nii.ac.jp/qis/first-quantum/e/forStudents/lecture/pdf/noise/chapter1.pdf]

• time average: time-averaged quantities for the \(i\)-th member of the ensemble
• ensemble average: ensemble-averaged quantities for all members of the ensemble at a certain time

where \(\theta\) is one member of the ensemble; \(p(x)dx\) is the probability that \(x\) is found among \([x, x + dx]\)

sample autocorrelation

[https://engineering.purdue.edu/VISE/ee438L/lab7/pdf/lab7b.pdf]

[http://www.signal.uu.se/Courses/CourseDirs/SignalbehandlingIT/forelas02.pdf]

ergodic vs. stationary

[https://bookdown.org/kevin_davisross/stat350-handouts/stationary.html]

Strict Sense Stationary (SSS) & Wide Sense Stationary (WSS)

[https://ece-research.unm.edu/bsanthan/ece541/station.pdf]

mean

Wiener-Khinchin theorem

Norbert Wiener proved this theorem for the case of a deterministic function in 1930; Aleksandr Khinchin later formulated an analogous result for stationary stochastic processes and published that probabilistic analogue in 1934. Albert Einstein explained, without proofs, the idea in a brief two-page memo in 1914

Continuous time

[https://www.robots.ox.ac.uk/~dwm/Courses/2TF_2011/2TF-L5.pdf]

Frank R. Kschischang. The Wiener-Khinchin Theorem [https://www.comm.utoronto.ca/~frank/notes/wk.pdf]

\(x(t)\), Fourier transform over a limited period of time \([-T/2, +T/2]\) , \(X_T(f) = \int_{-T/2}^{T/2}x(t)e^{-j2\pi ft}dt\)

With Parseval's theorem \[ \int_{-T/2}^{T/2}|x(t)|^2dt = \int_{-\infty}^{\infty}|X_T(f)|^2df \] So that \[ \frac{1}{T}\int_{-T/2}^{T/2}|x(t)|^2dt = \int_{-\infty}^{\infty}\frac{1}{T}|X_T(f)|^2df \]

where the quantity, \(\frac{1}{T}|X_T(f)|^2\) can be interpreted as distribution of power in the frequency domain

For each \(f\) this quantity is a random variable, since it is a function of the random process \(x(t)\)

The power spectral density (PSD) \(S_x(f )\) is defined as the limit of the expectation of the expression above, for large \(T\): \[ S_x(f) = \lim _{T\to \infty}\mathrm{E}\left[ \frac{1}{T}|X_T(f)|^2 \right] \]

The Wiener-Khinchin theorem ensures that for well-behaved wide-sense stationary processes the limit exists and is equal to the Fourier transform of the autocorrelation \[\begin{align} S_x(f) &= \int_{-\infty}^{+\infty}R_x(\tau)e^{-j2\pi f \tau}d\tau \\ R_x(\tau) &= \int_{-\infty}^{+\infty}S_x(f)e^{j2\pi f \tau}df \end{align}\]

Note: \(S_x(f)\) in Hz and inverse Fourier Transform in Hz (\(\frac{1}{2\pi}d\omega = df\))

Topic 6 Random Processes and Signals [https://www.robots.ox.ac.uk/~dwm/Courses/2TF_2021/N6.pdf]

Example

Remember: impulse scaling

\[ \cos(2\pi f_0t) \overset{\mathcal{F}}{\longrightarrow} \frac{1}{2}[\delta(f -f_0)+\delta(f+f_0)] \]

due to \(\cos(\omega_0 t +\phi_0) = \sin(\omega_0 t +\phi_0 + \frac{\pi}{2})\)

Discrete time

Diniz PSR, da Silva EAB, Netto SL. Digital Signal Processing: System Analysis and Design. 2nd ed. Cambridge University Press; 2010.

filtered by a linear time-invariant system

ACF of discrete-time sinusoid. Google AI Mode [https://share.google/aimode/IHyr7o8jLUMx2Leb3]

SIMG-713 Noise and Random Processes Spring 2002 . Lecture 15 Power Spectrum Estimation [https://www.cis.rit.edu/class/simg713/Lectures/Lecture713-15-4.pdf]

Properties of the Fourier Transform for Discrete-Time Signals [https://www.comm.utoronto.ca/dkundur/course_info/362/EmanHammadDTFT2.pdf]

\[ \frac{1}{2\pi}F^{-1}\{R_{xx}\}d\omega = \frac{1}{2\pi}F^{-1}\{R_{xx}\}d(2\pi f T)=T\cdot F^{-1}\{R_{xx}\}df = P_{xx}(f)df \] power spectral density of a discrete-time random process \(\{x(n)\}\) is given by \[ P_{xx}(f) =T\cdot F^{-1}\{R_{xx}\} \]

PSD & ESD

David Murray. Topic 5 Energy & Power Spectra, and Correlation [https://www.robots.ox.ac.uk/~dwm/Courses/2TF_2011/2TF-L5.pdf]

Finite Energy signals & Finite Power signals

2.161 Signal Processing - Continuous and Discrete Fall Term 2008 Lecture 22 [pdf]

Sklar, Bernard. Digital communications: fundamentals and applications. Pearson, 2021.

Rice's representation of WSS

Papoulis, A., & Pillai, S. U. (2002). Probability, random variables, and stochastic processes (4th ed.). McGraw-Hill

Po-Ning Chen, Chapter 10 Random Walks and Other Applications [https://video.ocw.nycu.edu.tw/pub/spr052/Handout/random10s16.pdf]

\(R_{nI}(\tau) = R_{nQ}(\tau)\) demonstrate spectra of \(n_I\) and \(n_Q\) to be equal

\(R_{nI,nQ}(\tau)=-R_{nQ,nI}(\tau)\) demonstrate \(n_I\) and \(n_Q\) are uncorrelated

arbitrary stationary process model

Darabi H. Radio Frequency Integrated Circuits and Systems. 2nd ed. Cambridge University Press; 2020.

uniform over a full period, \(0 \le \phi_k < 2\pi\) makes the model stationary

autocorrelation: the product is formed within each realization first, and then averaged over the ensemble

A member of the ensemble is a whole waveform, not a single time sample. One draw of the pair \((F,\phi) = (f_0, \phi_0)\) determines the sample function \(v(t) = e^{j(2\pi f_0 t + \phi_0)}\) for all \(t\) simultaneously. Writing the process as \(v(t;\omega)\) where the outcome \(\omega \leftrightarrow (f_0,\phi_0)\), the autocorrelation is \[ R_v(t+\tau, t) = E_\omega\big[v(t+\tau;\omega)\,v^*(t;\omega)\big], \] with the same \(\omega\) in both factors. You pick one member, read it at two times, multiply, and only then average over which member you picked. So the cancellation \[ v(t+\tau)v^*(t) = e^{j(2\pi F(t+\tau)+\phi)}e^{-j(2\pi Ft+\phi)} = e^{j2\pi F\tau} \] happens inside each realization, before any averaging: whatever \(\phi_0\) that member has, it cancels for that member. The expectation then only sees the leftover randomness in \(F\).

You can see it in the explicit integral over the joint density — there is one integration variable per random variable, shared by both factors: \[ E[v(t+\tau)v^*(t)] = \int_0^{2\pi}\!\!\int_{-\infty}^{\infty}\textcolor{blue}{ \underbrace{e^{j(2\pi f(t+\tau)+\varphi)}\,e^{-j(2\pi f t+\varphi)}}_{\text{same } f,\ \text{same }\varphi}} \, f_F(f)\,\frac{1}{2\pi}\,df\,d\varphi = \int_{-\infty}^{\infty} e^{j2\pi f\tau} f_F(f)\,df. \]

sinewaves discrete approximate for continuous white noise

A. A. Abidi and D. Murphy, "How to Design a Differential CMOS LC Oscillator," in IEEE Open Journal of the Solid-State Circuits Society, vol. 5, pp. 45-59, 2025 [https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=10818782]

suppose \(\color{blue}n(t) = \sum_i N[i]e^{ji\omega_0 t}\) where \(\color{blue}N[i] = \sigma\, e^{j\theta_i} \quad \theta_i \ \text{i.i.d. } \mathcal{U}(-\pi, +\pi]\)

the three related quantities are: \[ |N[i]| = \sigma \quad(\text{deterministic}), \qquad \langle N[i]\rangle = \sigma\,\langle e^{j\theta_i}\rangle = 0, \qquad N[i]\,\overline{N[i]} = \sigma e^{j\theta_i}\cdot \sigma e^{-j\theta_i} = \sigma^2. \] with the definition of the (ensemble) autocorrelation of a complex process \[ R_n(\tau) = \big\langle\, n(t+\tau)\,\overline{n(t)}\,\big\rangle = \sum_i \sum_k \big\langle N[i]\,\overline{N[k]}\big\rangle\, e^{j(i-k)\omega_0 t}\, e^{ji\omega_0 \tau} = \sum_i \sigma^2\, e^{ji\omega_0 \tau} \] The delta-function limit is then a Riemann sum: with \(\color{blue}\sigma^2 = N^2\Delta f\) and \(\omega_0 = 2\pi\Delta f\), \[ R_n(\tau) = \sum_i N^2\,e^{j2\pi (i\Delta f) \tau}\,\Delta f \;\xrightarrow{\;\Delta f \to 0\;}\; N^2\!\int_{-\infty}^{\infty} e^{j2\pi f\tau}\,df = N^2\delta(\tau), \] recovering the ideal white-noise autocorrelation stated in the paper

\[ \color{blue}\boxed{ \text{fixed magnitude + uniform phase} \Rightarrow \text{approximately Gaussian for many tones} } \]

whereas \[ \boxed{ \text{complex Gaussian coefficients} \Rightarrow \text{exactly Gaussian band-limited noise} }. \] If every sinusoid has a fixed amplitude and only its phase is random, \[ N_k = \sqrt{P_k}e^{j\Theta_k}, \] then a finite sum is not exactly Gaussian. However, when many independent components are added, the time-domain distribution becomes approximately Gaussian by the central limit effect.

For an exactly Gaussian frequency-domain construction, the spectral coefficients should be complex Gaussian: \[ N_k = N_{I,k}+jN_{Q,k}, \] where \[ N_{I,k},N_{Q,k} \sim \mathcal N(0,\sigma_k^2). \] In that case: \[ \Theta_k\sim\mathcal U(-\pi,\pi], \] but the magnitude is also random and has a Rayleigh distribution

LTI Filtering of WSS process

CT Deterministic Autocorrelation Function

Topic 6 Random Processes and Signals [https://www.robots.ox.ac.uk/~dwm/Courses/2TF_2021/N6.pdf]

Alan V. Oppenheim, Introduction To Communication, Control, And Signal Processing [https://ocw.mit.edu/courses/6-011-introduction-to-communication-control-and-signal-processing-spring-2010/a6bddaee5966f6e73450e6fe79ab0566_MIT6_011S10_notes.pdf]

Balu Santhanam, Probability Theory & Stochastic Process 2020: LTI Systems and Random Signals [https://ece-research.unm.edu/bsanthan/ece541/LTI.pdf]

\[ R_{yy}(\tau) = h(\tau)*R_{xx}(\tau)*h(-\tau) =R_{xx}(\tau)*h(\tau)*h(-\tau) \]

why \(\overline{R}_{hh}(\tau) \overset{\Delta}{=} h(\tau)*h(-\tau)\) is autocorrelation ? the proof is as follows:

\[\begin{align} \overline{R}_{hh}(\tau) &= h(\tau)*h(-\tau) \\ &= \int_{-\infty}^{\infty}h(x)h(-(\tau - x))dx \\ &= \int_{-\infty}^{\infty}h(x)h(-\tau + x)dx \\ &=\int_{-\infty}^{\infty}h(x+\tau)h(x)dx \end{align}\]

Time Reversal \[ x(-t) \overset{FT}{\longrightarrow} X(-j\omega) \]

if \(x(t)\) is real, then \(X(j\omega)\)​ has conjugate symmetry \[ X(-j\omega) = X^*(j\omega) \]

DT Deterministic Autocorrelation Function

\[ c_{hh}[l] = \sum_{k=-\infty}^{\infty}h[k]h[l+k]=\sum_{k=-\infty}^{\infty}h[-l+k]h[k]=\sum_{k=-\infty}^{\infty}h[-(l-k)]h[k]=h[l]*h[-l] \]

Periodogram

The periodogram is in fact the Fourier transform of the aperiodic correlation of the windowed data sequence

estimating continuous-time stationary random signal

The sequence \(x[n]\) is typically multiplied by a finite-duration window \(w[n]\), since the input to the DFT must be of finite duration. This produces the finite-length sequence \(v[n] = w[n]x[n]\)

\[\begin{align} \hat{P}_{ss}(\Omega) &= \frac{|V(e^{j\omega})|^2}{LU} \\ &= \frac{|V(e^{j\omega})|^2}{\sum_{n=0}^{L-1}(w[n])^2} \tag{1}\\ &= \frac{L|V(e^{j\omega})|^2}{\sum_{k=0}^{L-1}(W[k])^2} \tag{2} \end{align}\]

That is, by \((1)\) \[ \hat{P}_{ss}(\Omega) = T_s\hat{P}_{xx(\omega)} = \frac{T_s|V(e^{j\omega})|^2}{\sum_{n=0}^{L-1}(w[n])^2}=\frac{|V(e^{j\omega})|^2}{f_{res}L\sum_{n=0}^{L-1}(w[n])^2} \]

That is, by \((2)\) \[ \hat{P}_{ss}(\Omega) = T_s\hat{P}_{xx(\omega)} = \frac{T_sL|V(e^{j\omega})|^2}{\sum_{k=0}^{L-1}(W[k])^2} = \frac{|V(e^{j\omega})|^2}{f_{res}\sum_{k=0}^{L-1}(W[k])^2} \]

!! ENBW

Periodic & Cyclostationary Processes

Darabi H. Radio Frequency Integrated Circuits and Systems. 2nd ed. Cambridge University Press; 2020.

A wide-sense cyclostationary process becomes wide-sense stationary when its time origin is shifted by an independent random variable uniformly distributed over one period \[ \boxed{ v(t)\text{ wide-sense cyclostationary} \quad \xrightarrow[\Theta\sim\mathcal U(0,T)]{v_s(t)=v(t-\Theta)} \quad v_s(t)\text{ wide-sense stationary}. } \]

Multirate Systems & Random Sequences

Balu Santhanam. ece541 Probability Theory & Stochastic Process: Random Signals and Multirate Systems [http://ece-research.unm.edu/bsanthan/ece541/rand.pdf]

WSS Random Sequences

autocorrelation function of WSS random sequences

psd of WSS random sequences

Interpretation of the psd

Equation 8.4-4 is permissible for cyclostationary waveforms

decimation

\[ \frac{1}{M}\int_{-Mx_0}^{Mx_0}f(\frac{x}{M})dx = \int_{-Mx_0}^{Mx_0}f(\frac{x}{M}) d\frac{x}{M} = \int_{-x_0}^{x_0} f(\acute{x}) d\acute{x} \]

where \(\acute{x} = \frac{x}{M}\)

interpolation

The resulting expanded random sequence is clearly nonstationary, because of the zero insertions.

This random sequences and processes is classified as being cyclostationary

psd of \(X_e[n]\), the expansion or the upsampled version of \(X[n]\)

\[ S_{X_eX_e}(\omega) = \frac{1}{L}S_{XX}(L\omega) \]

where \(L\) is upsampling factor

apply \(X_e[n]\) to an ideal lowpass filter with bandwidth \([-\pi/2 , +\pi/2]\) and gain of \(2\) or \(L\)

\[ S_{YY}(\omega) = \left\{ \begin{array}{cl} L \cdot S_{XX}(L\omega), &\ |\omega|\leq \pi/L \\ 0, &\ \pi/L \lt |\omega| \leq \pi \end{array} \right. \]

Stark H, Woods JW. Probability, Statistics, and Random Processes for Engineers, 3rd [pdf]

—, 3th Ed Solution Manual [https://www.scribd.com/document/353335818/Stark-Woods-3th-Ed-Manual#page=212]

General case with upsampling factor \(L\)

\[\begin{align} &\mathrm{E}\{|\sum_{n=-N}^N X_e[n]e^{-j\omega n}|^2\}\\ &= \sum_{n=-N}^N\sum_{l=-N}^NX_e[n]\cdot X_e^*[l]\cdot e^{-j\omega(n-l)}\\ &= \sum_{n=-N}^N\sum_{l=-N}^NX[\frac{n}{L}]\cdot X^*[\frac{l}{L}]\cdot e^{-j\omega(n-l)}\\ &= \sum_{k=-N/L}^{N/L}\sum_{m=-N/L}^{N/L}X[k]\cdot X^*[m]\cdot e^{-jL\omega (k-m)}\\ &= \sum_{k=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}R_{XX}[k-m]\cdot e^{-j\omega L(k-m)}\cdot \mathcal{rect}[\frac{k}{2N/L}]\cdot \mathcal{rect}[\frac{m}{2N/L}]\\ &= \sum_{i=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}R_{XX}[i]\cdot e^{-jL\omega i}\cdot \mathcal{rect}[\frac{i+m}{2N/L}]\cdot \mathcal{rect}[\frac{m}{2N/L}]\\ &= \sum_{i=-\infty}^{\infty}R_{XX}[i]\cdot e^{-jL\omega i} \cdot \frac{2N}{L}\left[1 -\frac{|i|}{2N/L} \right] \end{align}\]

Then \[\begin{align} S_{X_eX_e}(\omega) &= \lim_{N\to \infty}\frac{1}{2N+1}\cdot \mathrm{E}\{|\sum_{n=-N}^N X_e[n]e^{-j\omega n}|^2\} \\ &= \frac{1}{L}\sum_{i=-\infty}^{\infty}R_{XX}[i]\cdot e^{-jL\omega i}\\ &= \frac{1}{L}S_{XX}(L\omega) \end{align}\]

Wiener Process (Brownian Motion)

Dennis Sun, Introduction to Probability: Lesson 49 Brownian Motion [https://dlsun.github.io/probability/brownian-motion.html]

Wiener process (also called Brownian motion)

NRZ PSD

Lecture 26 Autocorrelation Functions of Random Binary Processes [https://bpb-us-e1.wpmucdn.com/sites.gatech.edu/dist/a/578/files/2003/12/ECE3075A-26.pdf]

Lecture 32 Correlation Functions & Power Density Spectrum, Cross-spectral Density [https://bpb-us-e1.wpmucdn.com/sites.gatech.edu/dist/a/578/files/2003/12/ECE3075A-32.pdf]

note \(\color{red}S_x(0)=0\)

Normal Distribution and Input-Referred Noise [https://a2d2ic.wordpress.com/2013/06/05/normal-distribution-and-input-referred-noise/]

Sampling & recovery of random process

Appendix 3-A. Power Spectrum of A Cyclostationary Process

power spectral density of random pulse sequence using (3.84)

reference

L.W. Couch, Digital and Analog Communication Systems, 8th Edition, 2013 [pdf]

Alan V Oppenheim, George C. Verghese, Signals, Systems and Inference, 1st edition [pdf]

R. Ziemer and W. Tranter, Principles of Communications, Seventh Edition, 2013 [pdf]

Stark H, Woods JW. Probability, Statistics, and Random Processes for Engineers, 4th ed. 2012 [pdf]

Kuchler, Ryan J. Theory of multirate statistical signal processing and applications. Monterey, California.: Naval Postgraduate School, 2005. [pdf]

J. R. Barry, E. A. Lee, and D. G. Messerschmitt, Digital Communication, 3rd ed., Boston, MA: Kluwer Academic Publishers, 2003.

Balu Santhanam. Fall 2020 ECE541 Probability Theory & Stochastic Process [https://ece-research.unm.edu/bsanthan/ece541/]

PSS and HB Overview

The steady-state response is the response that results after any transient effects have dissipated.

The large signal solution is the starting point for small-signal analyses, including periodic AC, periodic transfer function, periodic noise, periodic stability, and periodic scattering parameter analyses.

Designers refer periodic steady state analysis in time domain as "PSS" and corresponding frequency domain notation as "HB"

Harmonic Balance Analysis

The idea of harmonic balance is to find a set of port voltage waveforms (or, alternatively, the harmonic voltage components) that give the same currents in both the linear-network equations and nonlinear-network equations

that is, the currents satisfy Kirchoff's current law

Define an error function at each harmonic, \(f_k\), where \[ f_k = I_{\text{LIN}}(k\omega) + I_{\text{NL}}(k\omega) \] where \(k=0, 1, 2,...,K\)

Note that each \(f_k\) is implicitly a function of all voltage components \(V(k\omega)\)

Newton Solution of the Harmonic-Balance Equation

Iterative Process and Jacobian Formulation

The elements of the Jacobian are the derivatives \[ \frac{\partial F_{\text{n,k}}}{\partial _{V_\text{m,l}}} \] where \(n\) and \(m\) are the port indices \((1,N)\), and \(k\) and \(l\) are the harmonic indices \((0,...,K)\)

Number of Harmonics & Time Samples

Initial Estimate

One important property of Newton's method is that its speed and reliability of convergence depend strongly upon the initial estimate of the solution vector.

Conversion Matrix Analysis

Large-signal/small-signal analysis, or conversion matrix analysis, is useful for a large class of problems wherein a nonlinear device is driven, or "pumped" by a single large sinusoidal signal; another signal, much smaller, is applied; and we seek only the linear response to the small signal.

The most common application of this technique is in the design of mixers and in nonlinear noise analysis

1. First, analyzing the nonlinear device under large-signal excitation only, where the harmonic-balance method can be applied
2. Then, the nonlinear elements in the device's equivalent circuit are then linearized to create small-signal, linear, time-varying elements
3. Finally, a small-signal analysis is performed

Element Linearized

Below shows a nonlinear resistive element, which has the \(I/V\) relationship \(I=f(V)\). It is driven by a large-signal voltage

Assuming that \(V\) consists of the sum of a large-signal component \(V_0\) and a small-signal component \(v\), with Taylor series \[ f(V_0+v) = f(V_0)+\frac{\mathrm{d}}{\mathrm{d}V}f(V)|_{V=V_0}\cdot v+\frac{1}{2}\frac{\mathrm{d}^2}{\mathrm{d}V^2}f(V)|_{V=V_0}\cdot v^2+... \] The small-signal, incremental current is found by subtracting the large-signal component of the current \[ i(v)=I(V_0+v)-I(V_0) \] If \(v \ll V_0\), \(v^2\), \(v^3\),... are negligible. Then, \[ i(v) = \frac{\mathrm{d}}{\mathrm{d}V}f(V)|_{V=V_0}\cdot v \]

\(V_0\) need not be a DC quantity; it can be a time-varying large-signal voltage \(V_L(t)\) and that \(v=v(t)\), a function of time. Then \[ i(t)=g(t)v(t) \] where \(g(t)=\frac{\mathrm{d}}{\mathrm{d}V}f(V)|_{V=V_L(t)}\)

The time-varying conductance \(g(t)\), is the derivative of the element's \(I/V\) characteristic at the large-signal voltage

By an analogous derivation, one could have a current-controlled resistor with the \(V/I\) characteristic \(V = f_R(I)\) and obtain the small-signal \(v/i\) relation \[ v(t) = r(t)i(t) \] where \(r(t) = \frac{\mathrm{d}}{\mathrm{d}I}f_R(I)|_{I=I_L(t)}\)

A nonlinear element excited by two tones supports currents and voltages at mixing frequencies \(m\omega_1+n\omega_2\), where \(m\) and \(n\) are integers. If one of those tones, \(\omega_1\) has such a low level that it does not generate harmonics and the other is a large-signal sinusoid at \(\omega_p\), then the mixing frequencies are \(\omega=\pm\omega_1+n\omega_p\), which shown in below figure

A more compact representation of the mixing frequencies is \[ \omega_n=\omega_0+n\omega_p \] which includes only half of the mixing frequencies:

• the negative components of the lower sidebands (LSB)
• and the positive components of the upper sidebands (USB)

For real signal, positive- and negative-frequency components are complex conjugate pairs

Shooting Newton

TODO 📅

Nonlinearity & Linear Time-Varying Nature

Nonlinearity Nature

The nonlinearity causes the signal to be replicated at multiples of the carrier, an effect referred to as harmonic distortion, and adds a skirt to the signal that increases its bandwidth, an effect referred to as intermodulation distortion

It is possible to eliminate the effect of harmonic distortion with a bandpass filter, however the frequency of the intermodulation distortion products overlaps the frequency of the desired signal, and so cannot be completely removed with filtering.

Time-Varying Linear Nature

linear with respect to \(v_{in}\) and time-varying

Given \(v_{in}(t)=m(t)\cos (\omega_c t)\) and LO signal of \(\cos(\omega_{LO} t)\), then \[ v_{out}(t) = \text{LPF}\{m(t)\cos(\omega_c t)\cdot \cos(\omega_{LO} t)\} \] and \[ v_{out}(t) = m(t)\cos((\omega_c - \omega_{LO})t) \]

A linear periodically-varying transfer function implements frequency translation

Linear Time Varying

The response of a relaxed LTV system at a time \(t\) due to an impulse applied at a time \(t − \tau\) is denoted by \(h(t, \tau)\)

The first argument in the impulse response denotes the time of observation.

The second argument indicates that the system was excited by an impulse launched at a time \(\tau\) prior to the time of observation.

Thus, the response of an LTV system not only depends on how long before the observation time it was excited by the impulse but also on the observation instant.

The output \(y(t)\) of an initially relaxed LTV system with impulse response \(h(t, \tau)\) is given by the convolution integral \[ y(t) = \int_0^{\infty}h(t,\tau)x(t-\tau)d\tau \] Assuming \(x(t) = e^{j2\pi f t}\) \[ y(t) = \int_0^{\infty}h(t,\tau)e^{j2\pi f (t-\tau)}d\tau = e^{j2\pi f t}\int_0^{\infty}h(t,\tau)e^{-j2\pi f\tau}d\tau \] The (time-varying) frequency response can be interpreted as \[ H(j2\pi f, t) = \int_0^{\infty}h(t,\tau)e^{-j2\pi f\tau}d\tau \] Linear Periodically Time-Varying (LPTV) Systems, which is a special case of an LTV system whose impulse response satisfies \[ h(t, \tau) = h(t+T_s, \tau) \] In other words, the response to an impulse remains unchanged if the time at which the output is observed (\(t\)) and the time at which the impulse is applied (denoted by \(t_1\)) are both shifted by \(T_s\) \[ H(j2\pi f, t+T_s) = \int_0^{\infty}h(t+T_s,\tau)e^{-j2\pi f\tau}d\tau = \int_0^{\infty}h(t,\tau)e^{-j2\pi f\tau}d\tau = H(j2\pi f, t) \] \(H(j2\pi f, t)\) of an LPTV system is periodic with timeperiod \(T_s\), it can be expanded as a Fourier series in \(t\), resulting in \[ H(j2\pi f, t) = \sum_{k=-\infty}^{\infty} H_k(j2\pi f)e^{j2\pi f_s k t} \] The coefficients of the Fourier series \(H_k(j2\pi f)\) are given by \[ H_k(j2\pi f) = \frac{1}{T_s}\int_0^{T_s} H(j2\pi f, t) e^{-j2\pi k f_s t}dt \]

Periodic small signal in SpectreRF

B. Boser,A, 2011EECS 240 Topic 6: Noise Analysis [https://mixsignal.wordpress.com/wp-content/uploads/2013/06/t06noiseanalysis_simone-1.pdf]

Vishal Saxena, "SpectreRF Periodic Analysis" [https://www.eecis.udel.edu/~vsaxena/courses/ece614/Handouts/SpectreRF%20Periodic%20Analysis.pdf]

Ashwin Kumar, Lecture 8: Basics of periodic steady-state (pss), pac and pxf simulation demos in Cadence SpectreRF [https://youtu.be/I9zkt1OTWB0]

pss, pac and pxf

1. LPV analyses start by performing a periodic analysis to compute the periodic operating point with only the large clock signal applied (the LO, the clock, the carrier, etc.).
2. The circuit is then linearized about this time-varying operating point (expand about the periodic equilibrium point with a Taylor series and discard all but the first-order term)
3. and the small information signal is applied. The response is calculated using linear time-varying analysis

Versions of this type of small-signal analysis exists for both harmonic balance and shooting methods

PAC is useful for predicting the output sidebands produced by a particular input signal

PXF is best at predicting the input images for a particular output

sampled pac

Sampled PAC (Spectre RF) Analysis - Strange results ? [https://designers-guide.org/forum/YaBB.pl?num=1590925194]

supply noise sensitivity: PSS+PAC or PSS+PXF [https://www.designers-guide.org/forum/YaBB.pl?num=1376500816]

Explanation for sampled PXF analysis [https://community.cadence.com/cadence_technology_forums/f/custom-ic-design/45055/explanation-for-sampled-pxf-analysis/1367253]

note: frequency axis is output

Which is the difference between "spectrum" sweep and "sideband" sweep in the PAC Direct Plot Form?[https://community.cadence.com/cadence_technology_forums/f/mixed-signal-design/56824/pac-simulation-sideband-sweep-parameter]

sampled pxf

Cadence RAK: Deterministic Jitter Measurement using SpectreRF

Sweeptype: relative + Relative Harmonic vs absolute — Output Frequency Sweep Range (Hz) \[ f_\text{abs} = f_\text{relative} + N_\text{relharmnum}\cdot f_\text{und} \]

note: frequency axis is input

relative + Relative Harmonic

1
2
3
4
5

pss  pss  fund=2.5G  harms=25  errpreset=conservative
+    annotate=status
pxf  (  Out1  0  Out1  0  )  pxf  crossingdirection=rise
+    thresholdvalue=1.65  ptvtype=sampled  sweeptype=relative  relharmnum=1
+    start=0  stop=1G  step=10M  maxsideband=1  annotate=status

Sweeptype: absolute

1
2
3
4
5

pss  pss  fund=2.5G  harms=25  errpreset=conservative
+    annotate=status
pxf  (  Out1  0  Out1  0  )  pxf  crossingdirection=rise
+    thresholdvalue=1.65  ptvtype=sampled  sweeptype=absolute  start=2.5G
+    stop=3.5G  step=10M  maxsideband=1  annotate=status

Frank Wiedmann, Using sampled pxf analysis to simulate deterministic jitter [https://community.cadence.com/cadence_technology_forums/f/custom-ic-design/51605/using-sampled-pxf-analysis-to-simulate-deterministic-jitter]

tran simulation verify higher frequency ripple introduce more jitter at output

sampled pac result support the opinion of Frank Wiedmann — harmonic 0 (with no additional sidebands) introduce maximum output

reference

Pavan, Shanthi, and Gabor C. Temes. Circuit Analysis for Analog, Mixed-Signal and RF Designers. Wiley-IEEE Press, 2026.

—, "Demystifying Linear Time Varying Circuits," IEEE Solid-State Circuits Society (SSCS) Webinar, 2016. [Online]. Available: IEEE SSCS Resource Center

—, "Reciprocity and Inter-Reciprocity: A Tutorial— Part I: Linear Time-Invariant Networks," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 70, no. 9, pp. 3413-3421, Sept. 2023, doi: 10.1109/TCSI.2023.3276700.

—, "Reciprocity and Inter-Reciprocity: A Tutorial—Part II: Linear Periodically Time-Varying Networks," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 70, no. 9, pp. 3422-3435, Sept. 2023, doi: 10.1109/TCSI.2023.3294298.

—, "Interreciprocity in Linear Periodically Time-Varying Networks With Sampled Outputs," in IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 61, no. 9, pp. 686-690, Sept. 2014, [https://sci-hub.jp/10.1109/TCSII.2014.2335393]

—. Introduction to Time - Varying Electrical Network. [https://youtube.com/playlist?list=PLyqSpQzTE6M8qllAtp9TTODxNfaoxRLp9]

—. EE5323: Advanced Electrical Networks (Jan-May. 2015) [https://www.ee.iitm.ac.in/vlsi/courses/ee5323/start]

K. S. Kundert, "Introduction to RF simulation and its application," in IEEE Journal of Solid-State Circuits, vol. 34, no. 9, pp. 1298-1319, Sept. 1999, doi: 10.1109/4.782091. [pdf]

—. (2006). Simulating Switched-Capacitor Filters with SpectreRF. URL:https://designers-guide.org/analysis/sc-filters.pdf

Stephen Maas, Nonlinear Microwave and RF Circuits, Second Edition , Artech, 2003.

Karti Mayaram. ECE 521 Fall 2016 Analog Circuit Simulation: Simulation of Radio Frequency Integrated Circuits [pdf1, pdf2]

The Value Of RF Harmonic Balance Analyses For Analog Verification: Frequency domain periodic large and small signal analyses. [https://semiengineering.com/the-value-of-rf-harmonic-balance-analyses-for-analog-verification/]

R. S. Ashwin Kumar. EE698W: Analog circuits for signal processing [https://home.iitk.ac.in/~ashwinrs/2022_EE698W.html]

Piet Vanassche, Georges Gielen, and Willy Sansen. 2009. Systematic Modeling and Analysis of Telecom Frontends and their Building Blocks (1st. ed.). Springer Publishing Company, Incorporated.

Beffa, Federico. (2023). Weakly Nonlinear Systems. 10.1007/978-3-031-40681-2.

Wereley, Norman. (1990). Analysis and control of linear periodically time varying systems.

Hameed, S. (2017). Design and Analysis of Programmable Receiver Front-Ends Based on LPTV Circuits. UCLA. ProQuest ID: Hameed_ucla_0031D_15577. Merritt ID: ark:/13030/m5gb6zcz. Retrieved from [https://escholarship.org/uc/item/51q2m7bx]

Matt Allen. Introduction to Linear Time Periodic Systems. [https://youtu.be/OCOkEFDQKTI]

Fivel, Oren. "Analysis of Linear Time-Varying & Periodic Systems." arXiv preprint arXiv:2202.00498 (2022).

RF Harmonic Balance Analysis for Nonlinear Circuits [https://resources.pcb.cadence.com/blog/2019-rf-harmonic-balance-analysis-for-nonlinear-circuits]

Steer, Michael. Microwave and RF Design (Third Edition, 2019). NC State University, 2019.

—. Harmonic Balance Analysis of Nonlinear RF Circuits - Case Study Index: CS_AmpHB [link]

Josh Carnes,Peter Kurahashi. "Periodic Analyses of Sampled Systems" URL:https://slideplayer.com/slide/14865977/

Article (20482538) Title: Why is pnoise sampled(jitter) different than pnoise timeaverage on a driven circuit?

Article (20467468) Title: The mathematics behind choosing the upper frequency when simulating pnoise jitter on an oscillator

Andrew Beckett. "Simulating phase noise for PFD-CP". URL:https://groups.google.com/g/comp.cad.cadence/c/NPisXTElx6E/m/XjWxKbbfh2cJ

Dr. Yanghong Huang. MATH44041/64041: Applied Dynamical Systems [https://personalpages.manchester.ac.uk/staff/yanghong.huang/teaching/MATH4041/default.htm]

Jeffrey Wong. Math 563, Spring 2020 Applied computational analysis [https://services.math.duke.edu/~jtwong/math563-2020/main.html]

—. Math 353, Fall 2020 Ordinary and Partial Differential Equations [https://services.math.duke.edu/~jtwong/math353-2020/main.html]

Tip of the Week: Please explain in more practical (less theoretical) terms the concept of "oscillator line width." [https://community.cadence.com/cadence_blogs_8/b/rf/posts/please-explain-in-more-practical-less-theoretical-terms-the-concept-of-quot-oscillator-line-width-quot]

Rubiola, E. (2008). Phase Noise and Frequency Stability in Oscillators (The Cambridge RF and Microwave Engineering Series). Cambridge: Cambridge University Press. doi:10.1017/CBO9780511812798

Dr. Ulrich L. Rohde, Noise Analysis, Then and Today [https://www.microwavejournal.com/articles/29151-noise-analysis-then-and-today]

Nicola Da Dalt and Ali Sheikholeslami. 2018. Understanding Jitter and Phase Noise: A Circuits and Systems Perspective (1st. ed.). Cambridge University Press, USA.

Kester, Walt. (2005). Converting Oscillator Phase Noise to Time Jitter. [https://www.analog.com/media/en/training-seminars/tutorials/MT-008.pdf]

Drakhlis, B.. (2001). Calculate oscillator jitter by using phase-noise analysis: Part 2 of two parts. Microwaves and Rf. 40. 109-119.

Explanation for sampled PXF analysis. [https://community.cadence.com/cadence_technology_forums/f/custom-ic-design/45055/explanation-for-sampled-pxf-analysis/1376140#1376140]

模拟放大器的低噪声设计技术2-3实践 아날로그 증폭기의 저잡음 설계 기법2-3실습 [https://youtu.be/vXLDfEWR31k]

2.2 How POP Really Works [https://www.simplistechnologies.com/documentation/simplis/ast_02/topics/2_2_how_pop_really_works.htm]

Jaeha Kim. Lecture 11. Mismatch Simulation using PNOISE [https://ocw.snu.ac.kr/sites/default/files/NOTE/7037.pdf]

Hueber, G., & Staszewski, R. B. (Eds.) (2010). Multi-Mode/Multi-Band RF Transceivers for Wireless Communications: Advanced Techniques, Architectures, and Trends. John Wiley & Sons. https://doi.org/10.1002/9780470634455

B. Boser,A. Niknejad ,S.Gambin 2011 EECS 240 Topic 6: Noise Analysis [https://mixsignal.files.wordpress.com/2013/06/t06noiseanalysis_simone-1.pdf]

In general, phase noise refers only to the random fluctuations of the phase or the zero crossings, whereas jitter may contain a deterministic (periodic) component

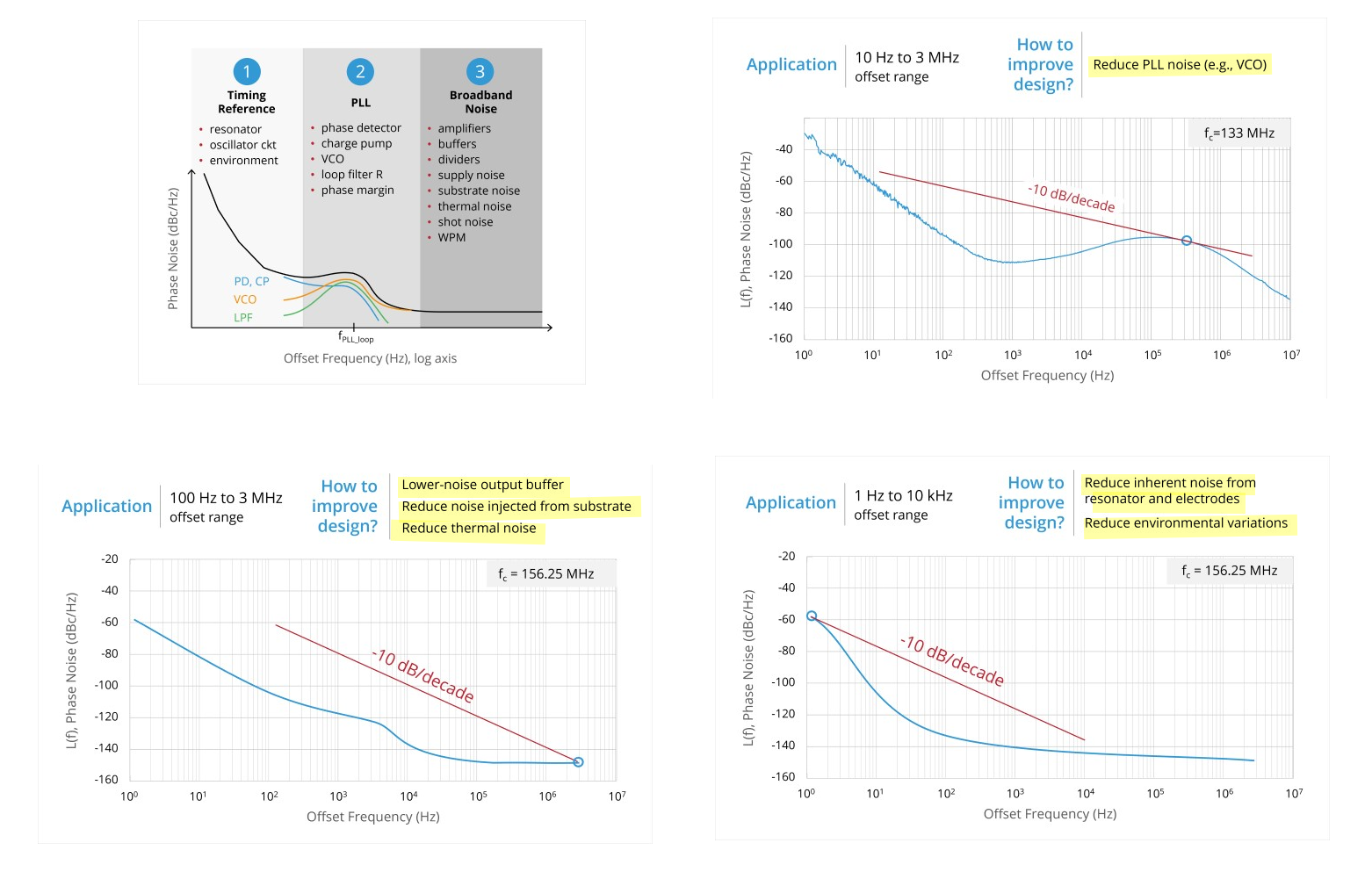
Phase Noise on \(log\) scale

How to Identify the Source of Phase Jitter through Phase Noise Plots [https://www.sitime.com/company/newsroom/blog/how-identify-source-phase-jitter-through-phase-noise-plots]

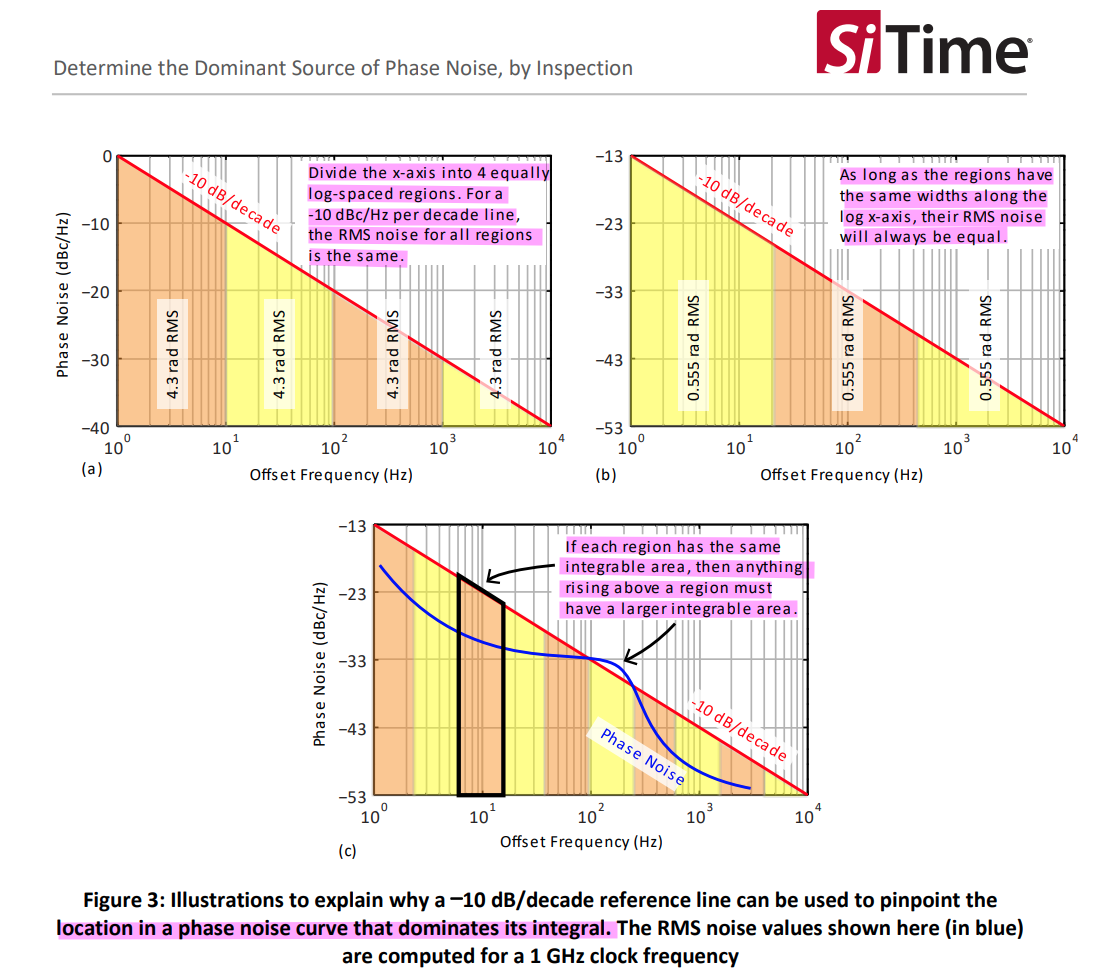
AN10072 Determine the Dominant Source of Phase Noise, by Inspection [https://www.sitime.com/support/resource-library/application-notes/an10072-determine-dominant-source-phase-noise-inspection]

4-minute Clinic: Determine the Dominant Source of Jitter by Inspection of Phase Noise Plot [https://youtu.be/2elHk3v45Pk]

Chembian Thambidurai, "Integrated Power of Thermal and Flicker Noise" [link]

a -10 dB/decade reference line can be used to pinpoint the location in a phase noise curve that dominates its integral

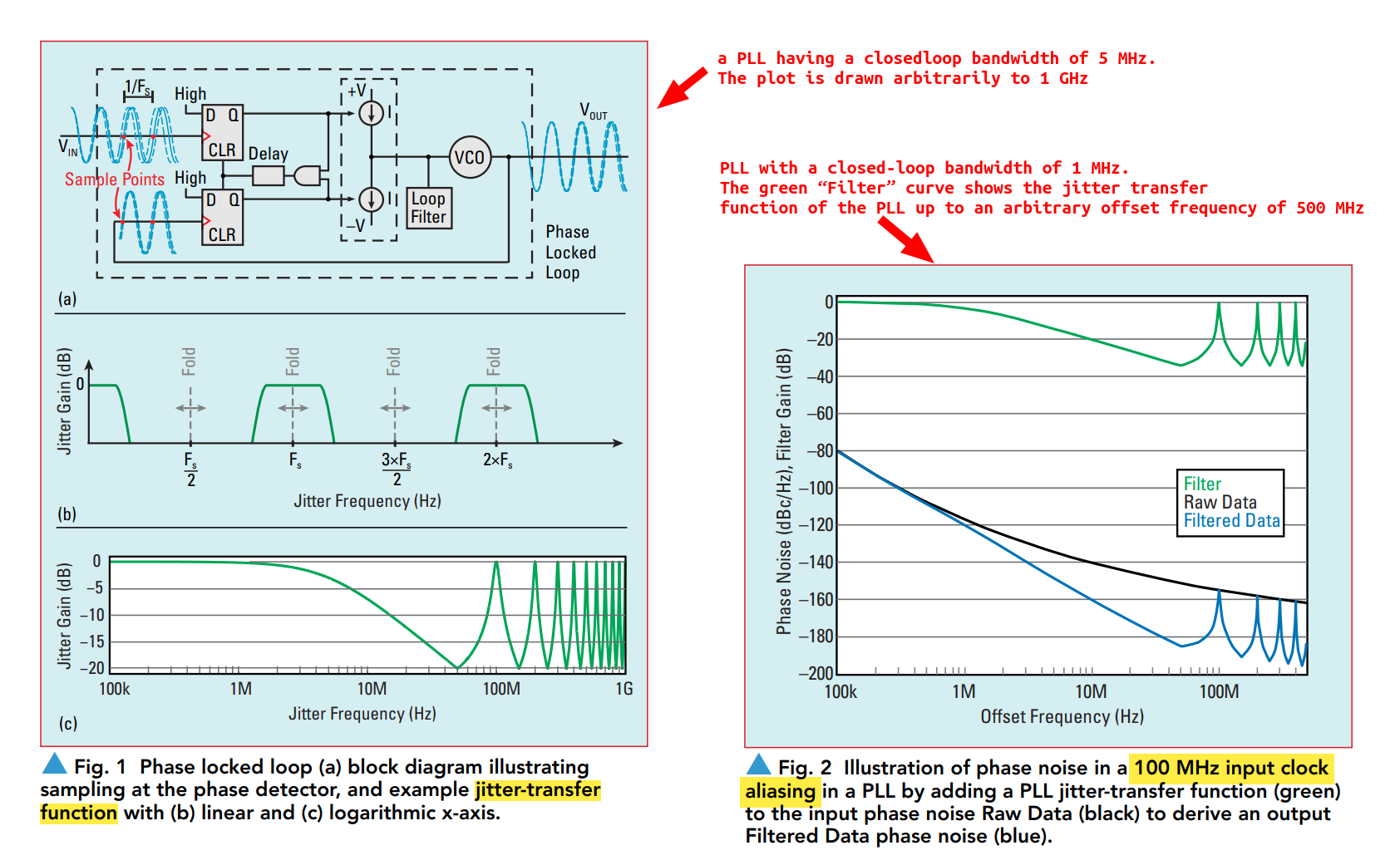
Reference-Clock Phase Noise in PLL

Gary Giust. How to Evaluate Reference-Clock Phase Noise in High-Speed Serial Links [expanded version], [compact version]

G. Richmond, "Refclk Fanout Best Practices for 8GT/s and 16GT/s Systems," PCI-SIG Developers Conference, June 7, 2017

Knowing how input phase noise aliases when sampled by a PLL

An alternate view of phase noise aliasing during the sampling process

• Instead of mirroring the jitter-transfer function located below \(F_S/2\) across spectral boundaries located at integer multiples of \(F_S/2\) (i.e. 50 MHz) as shown in Figure 2 (a)
• we could alternatively fold the portion of the Raw Data curve located above \(F_S/2\) across these spectrum boundaries to appear below \(F_S/2\) as shown in Figure 2 (b)

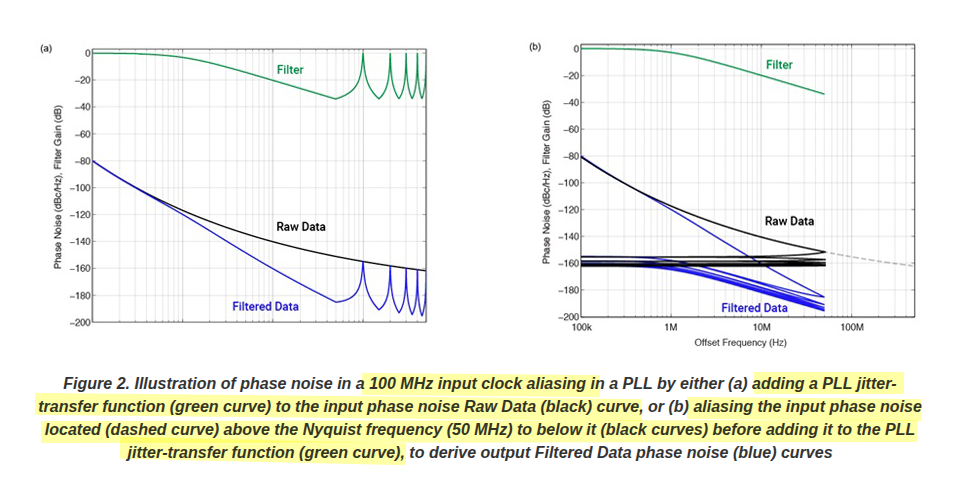
Integrating the combined area under each Filtered Data curve shown in Figure 2 (b) is mathematically equivalent to integrating the entire Filtered Data curve shown in Figure 2 (a)

Phase Noise Analyzer vs TIE jitter using Real-time Oscilloscope

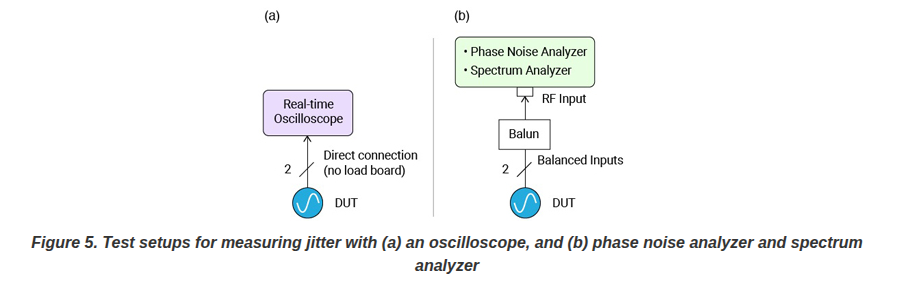
Since an oscilloscope observes jitter similar to a real system, we regard its result as the gold standard against which other methods may be judged

Flat Phase Noise Extension to twice the clock frequency

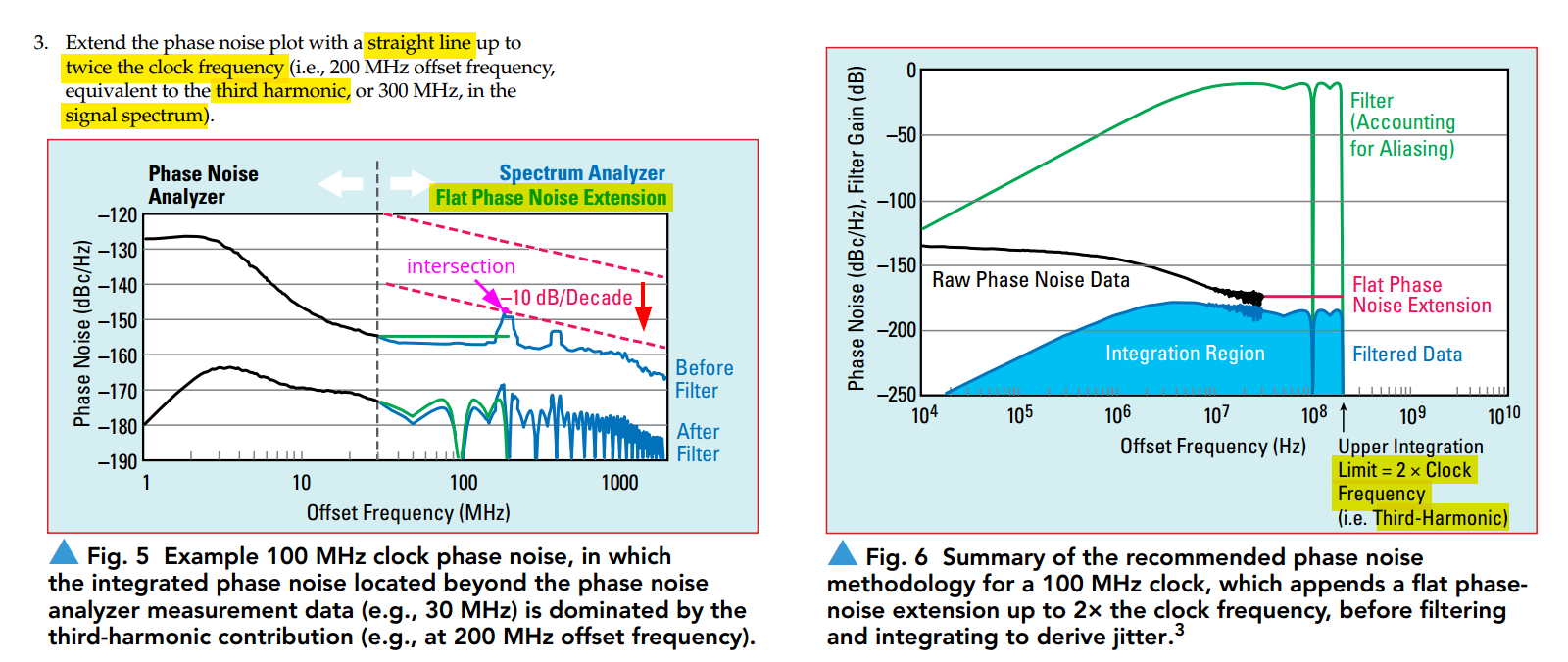
Phase Noise Aliasing & Integration Limits

Y. Zhao and B. Razavi, "Phase Noise Integration Limits for Jitter Calculation,"[https://www.seas.ucla.edu/brweb/papers/Conferences/YZ_ISCAS_22.pdf]

G. Giust, "Phase Noise Aliases as TIE Jitter," Signal Integrity Journal, July 23, 2018 [https://www.signalintegrityjournal.com/articles/912-phase-noise-aliases-as-tie-jitter]

Methods of jitter simulation in Cadence [https://www.rfinsights.com/cadence/sampled-vs-time-average-jitter/]

These two types of measurements deliver the same rms jitter of \(f_{CK}\)

• both rising and falling: integrated from \(-f_{CK}\) to \(+f_{CK}\)
• only the rising (or falling) edges: integrated from \(-f_{CK}/2\) to \(+f_{CK}/2\)

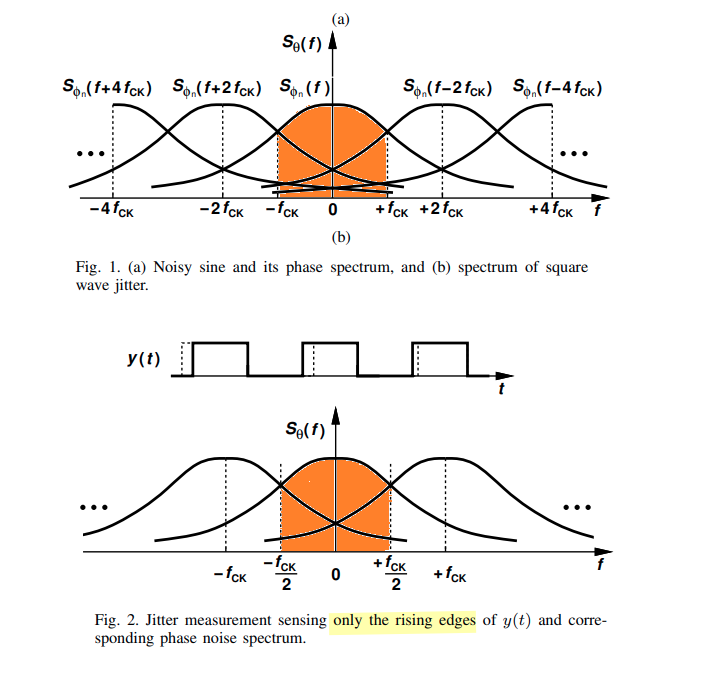
temporal autocorrelation and Wiener-Khinchin theorem is more appropriate to arise rms value

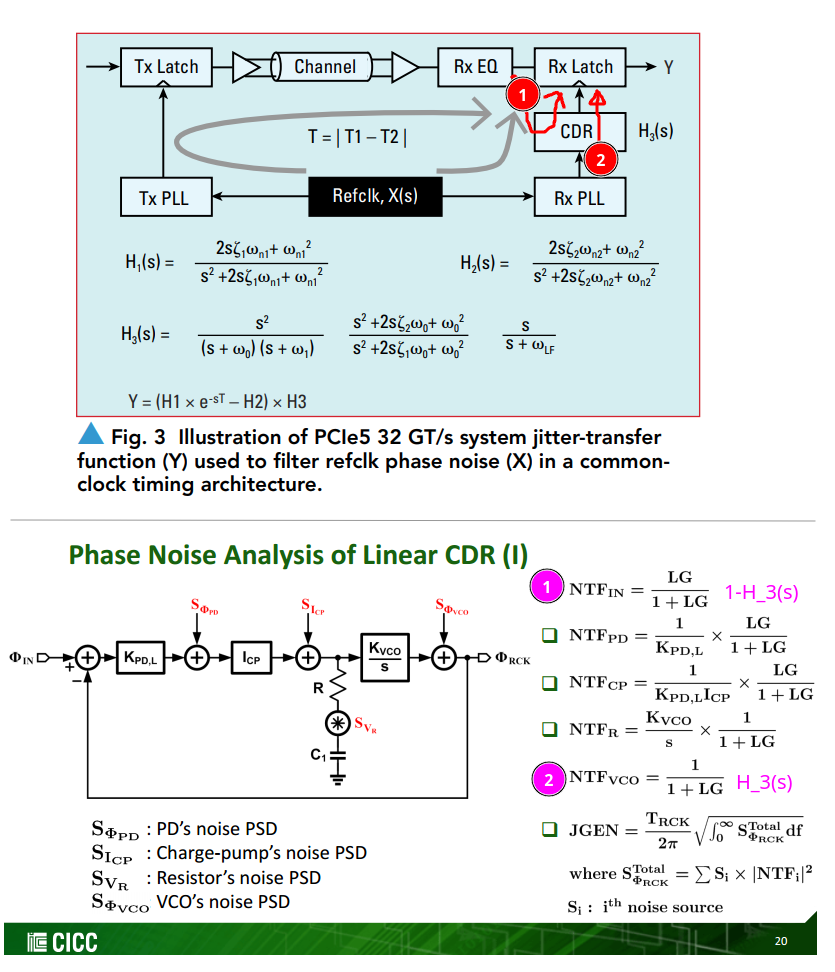
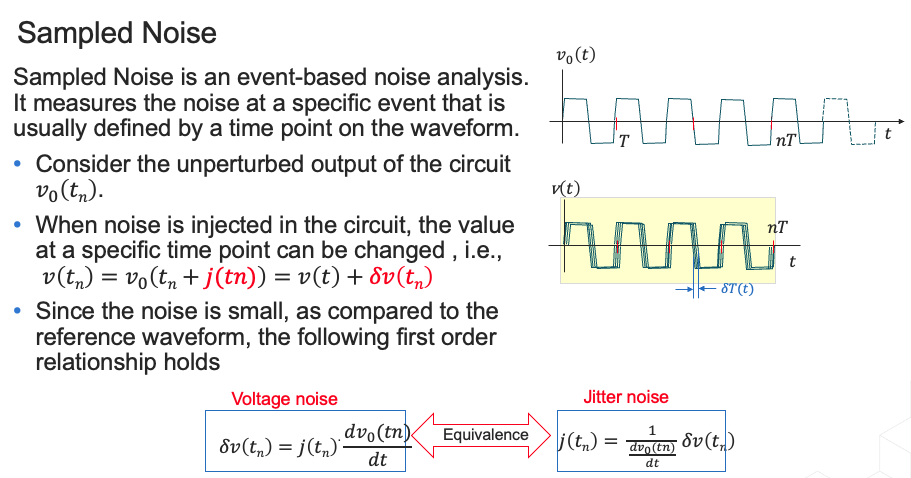
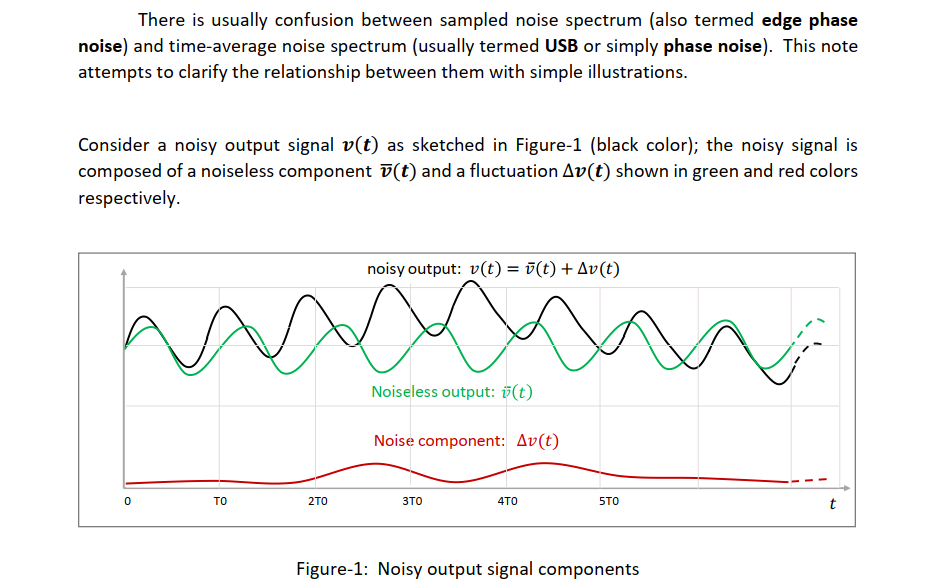
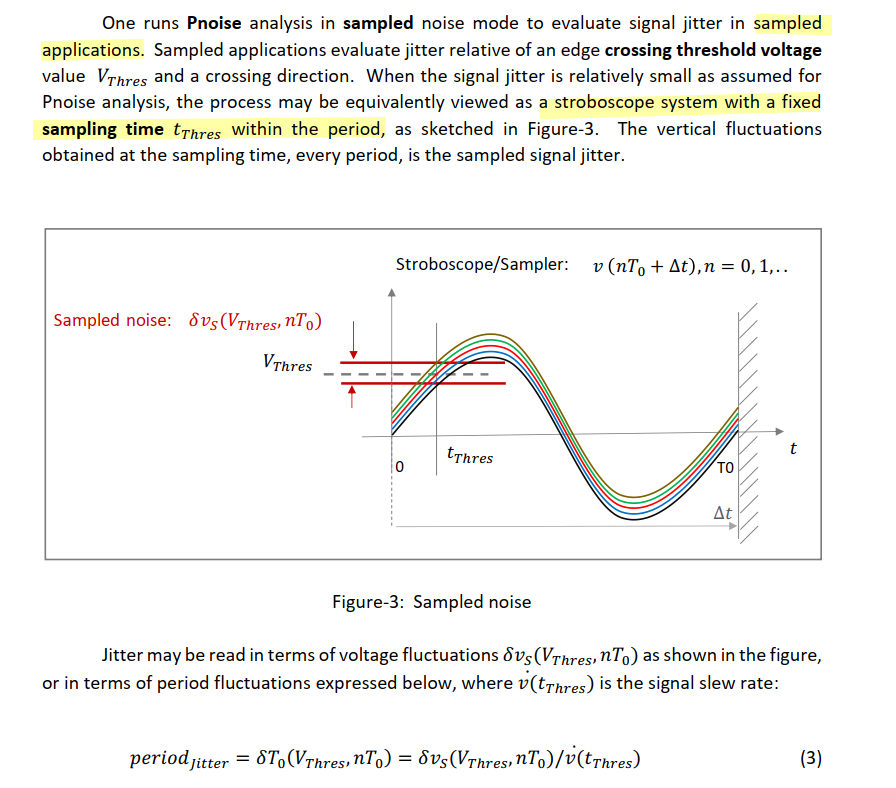
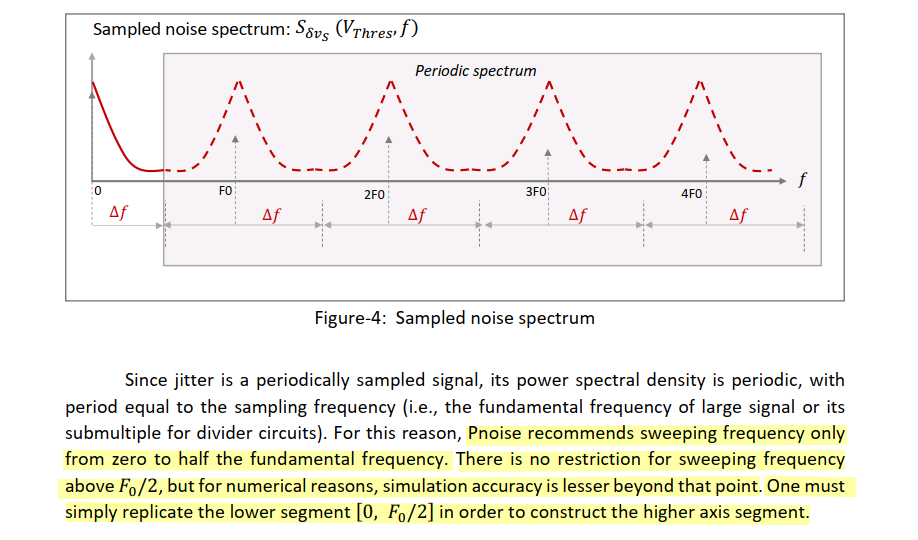
Jitter and Edge phase noise

[https://community.cadence.com/cadence_technology_forums/f/custom-ic-design/56929/how-to-derive-edge-phase-noise-from-output-noise-in-sampled-pnoise-simulation/1388888]

Shawn Logan, Summary of Study of Cadence Sampled Phase Noise and Jitter Definitions with a Comparison to Conventional Time Interval Error (TIE) for a Driven Circuit [www.dropbox.com/s/3m531dl4fl7bwbr/jee_computation_example_sml_032823v1p0.pdf]

timeaverage noise & sampled noise spectrum

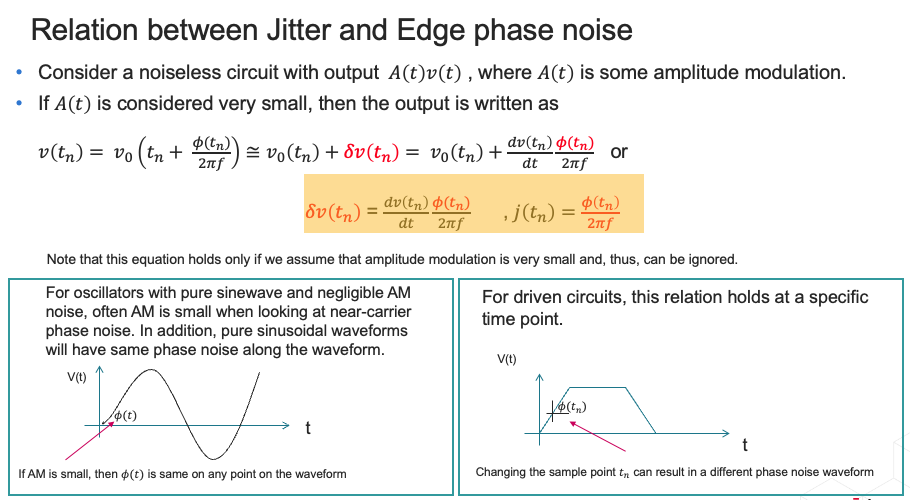
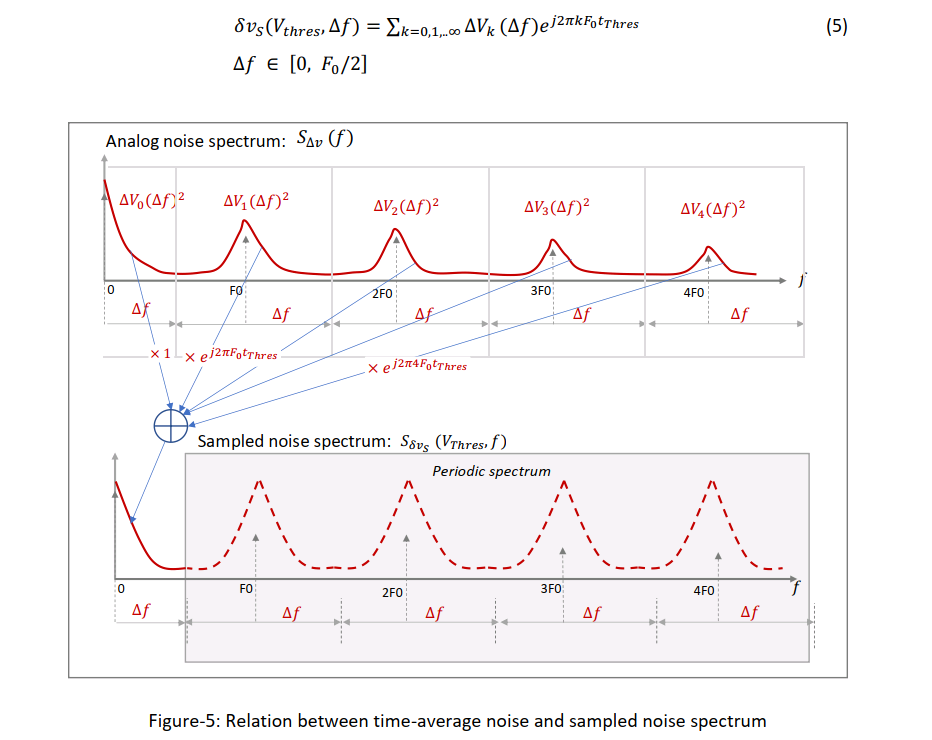
timeaverage noise (phase-noise) & sampled noise (edge-phase noise or jitter) spectrum

Time-average noise analysis

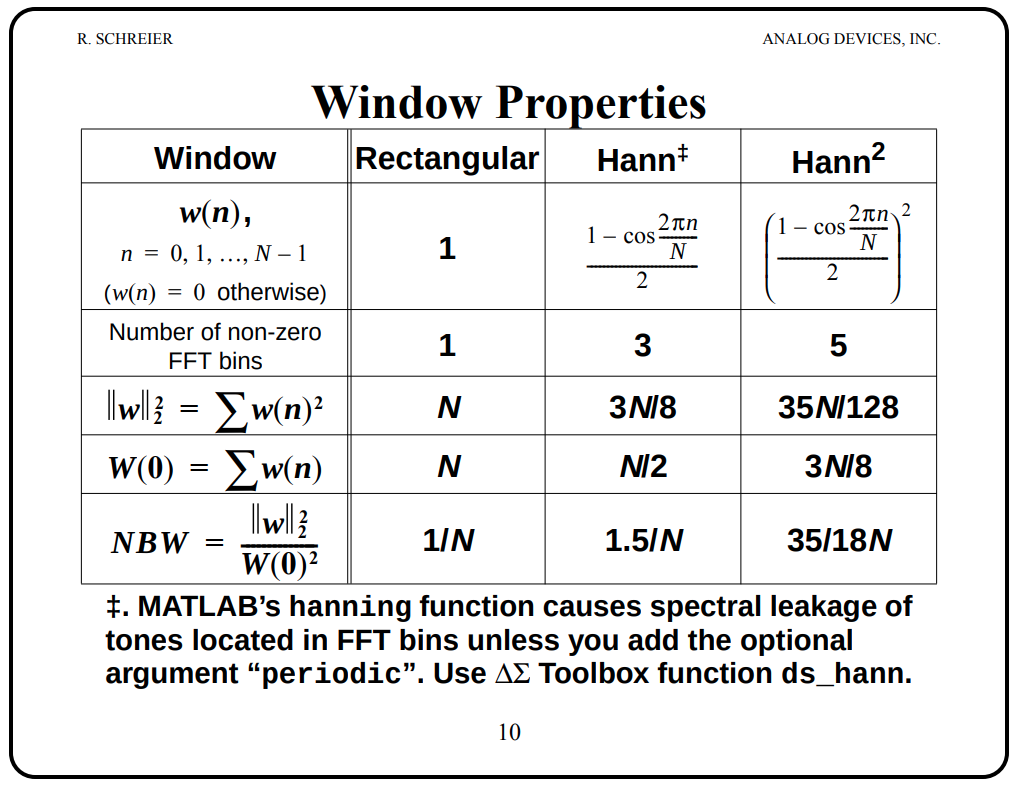
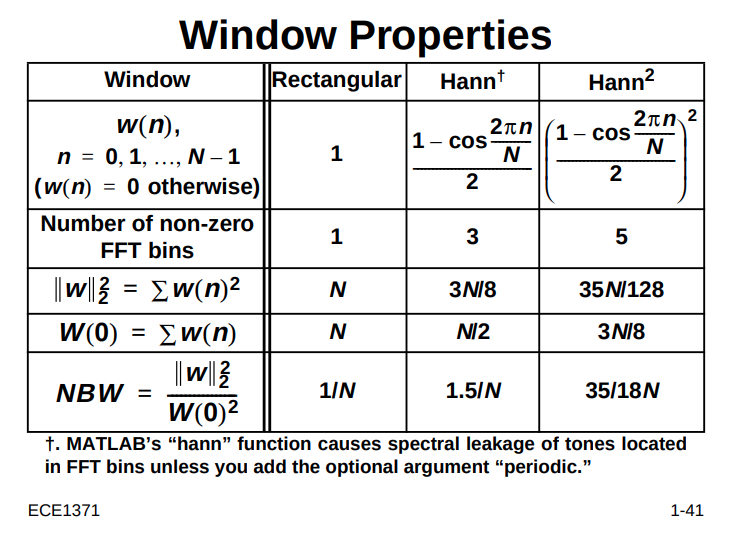
\(S_{\Delta f}(f)\) between \([\Delta f, F_0/2]\) may be less than that of other harmonic window

Sampled noise analysis

correlation

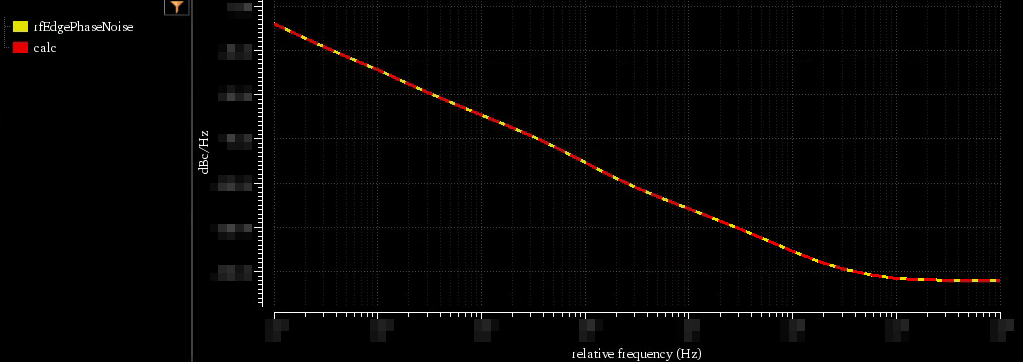
VCO Phase Noise

pnoise - timeaverage

1. Direct Plot/Pnoise/Phase Noise or

   

2. manually calculate by definition

   

3. output noise with unit dBc

   Direct Plot/Pnoise/Output Noise Units:dBc/Hz and Noise convention: SSB

   

The above method 2 and 3 only apply to timeaveage pnoise simulation,

pnoise - sampled(jitter)/Edge Crossing

Direct Plot/Pnoise/Edge Phase Noise or

Another way, the following equation can also be used for sampled(jitter)/Edge Crossing

1

PhaseNoise(dBc/Hz) = dB20( OutputNoise(V/sqrt(Hz)) / slopeCrossing / Tper*twoPi ) - dB10(2)

where dB10(2) is used to obtain SSB from DSB

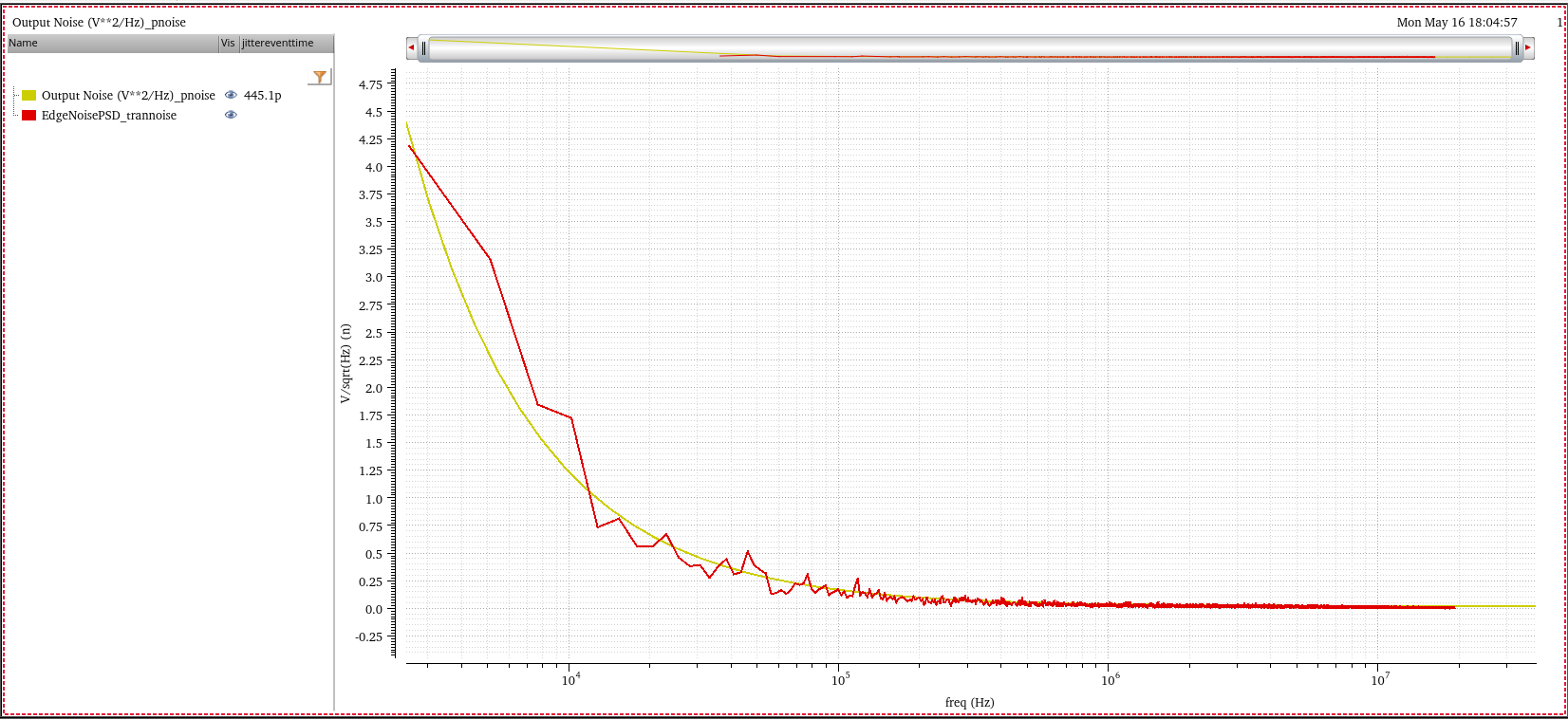
Output Noise of sampled(jitter) pnoise

The last section's Output Noise (V**2/Hz) can be obtained by transient noise simulation

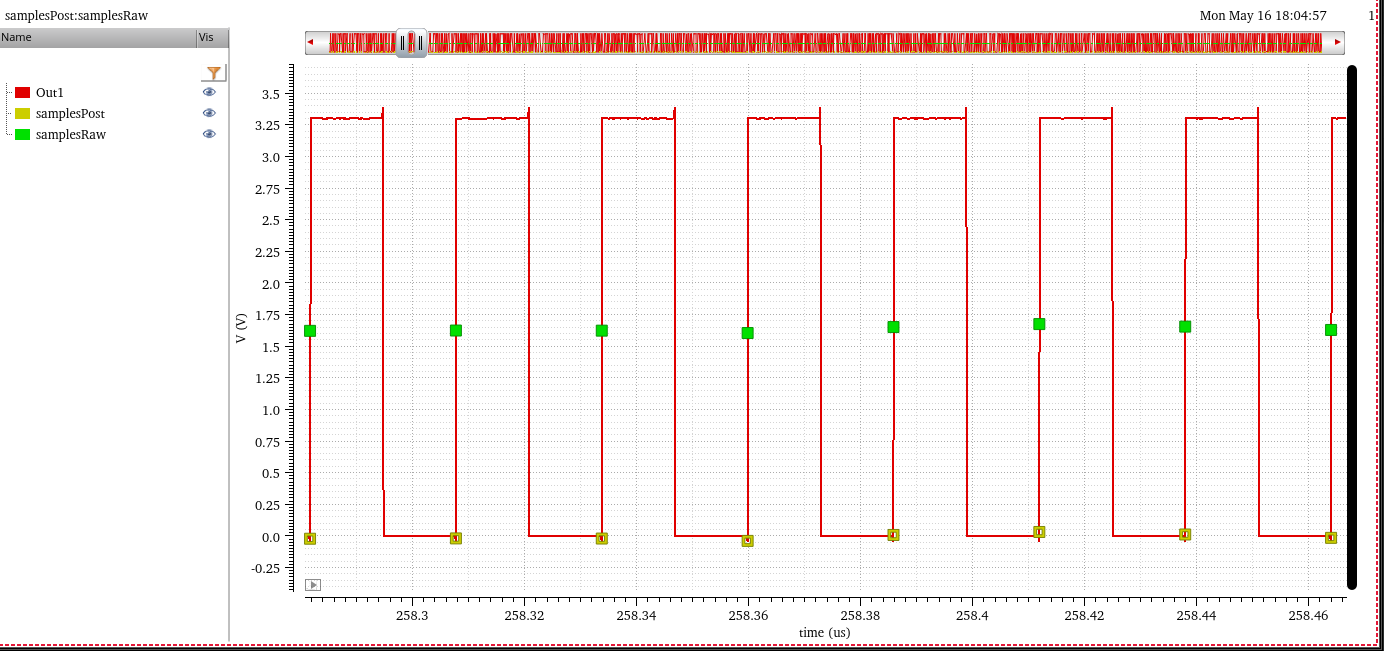
The idea is that sample waveform with ideal clock, subtract DC offset, then fft(psd)

• samplesRaw = sample(wv)
• samplePost = samplesRaw - average(samplesRaw)
• Output Noise (V**2/Hz) = psd(samplePost)

Expression:

The computation cost is typically very high, and the accuracy is lesser as compared to PSS/Pnoise

Harmonic Balance simulation

Y. Zhao and B. Razavi, "Phase Noise Integration Limits for Jitter Calculation," 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 2022 [http://seas.ucla.edu/brweb/papers/Conferences/YZ_ISCAS_22.pdf]

Tawna, PNOISE Noise Type Time Average vs. Sampled Jitter [https://community.cadence.com/cadence_technology_forums/f/rf-design/65882/pnoise-noise-type-time-average-vs-sampled-jitter/1408176]

How can I set the stop frequency for a sampled pnoise/hbnoise analysis to be half the PSS fundamental?

The mathematics behind choosing the upper frequency when simulating pnoise jitter on an oscillator

Oversample and Number of Harmonics setting

Pnoise Sampled(jitter): Sampled Phase Option

• Identical to noisetype=timedomain in old GUI
• Use model:
  • Sampleds Per Period: number of ponits
  • Add Specific Points: specific time point, still time points

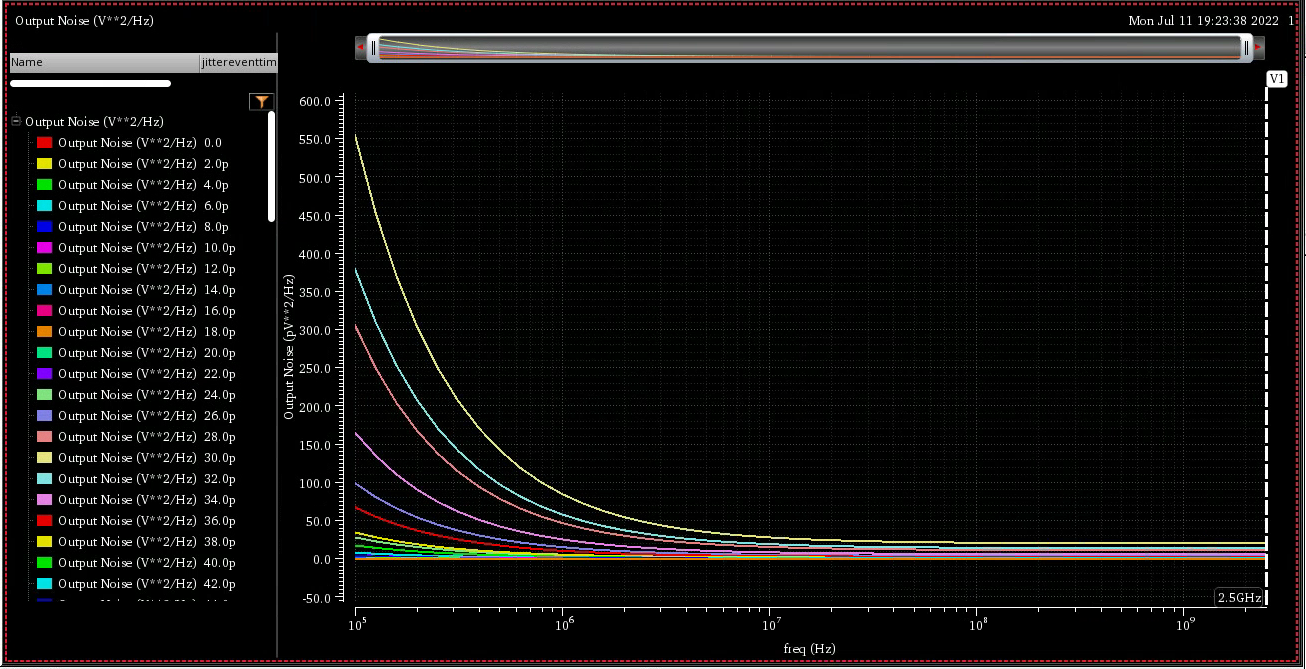
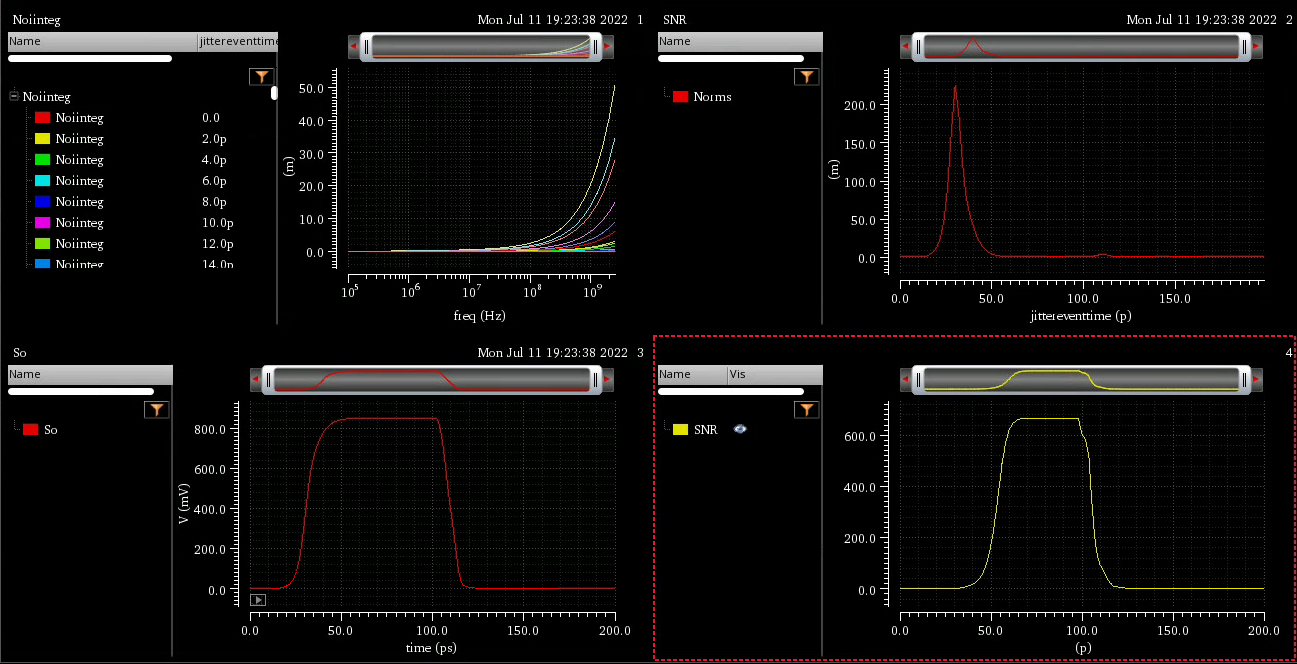
pss beat freq = 5GHz

pnoise sweeptype: absolute, from 100k to 2.5GHz

Transient noise

phase noise from transient noise analysis

1. The Phase Noise function is now available in the Direct Plot form (Results-Direct Plot-Main Form) after Transient Analysis is run
   • Absolute jitter Method
   • Direct Power Spectral Density Method
2. PN phase noise function
   • Absolute jitter Method
   • Direct Power Spectral Density Method

Absolute jitter Method: Phase noise is defined as the power spectral density of the absolute jitter of an input waveform

and absolute jitter method is the default method

In below discussion, we only think about the absolute jitter method

PSD & Phase Noise

• phase noise is single-sideband
• psd is double-sideband
• Then the ratio is 2

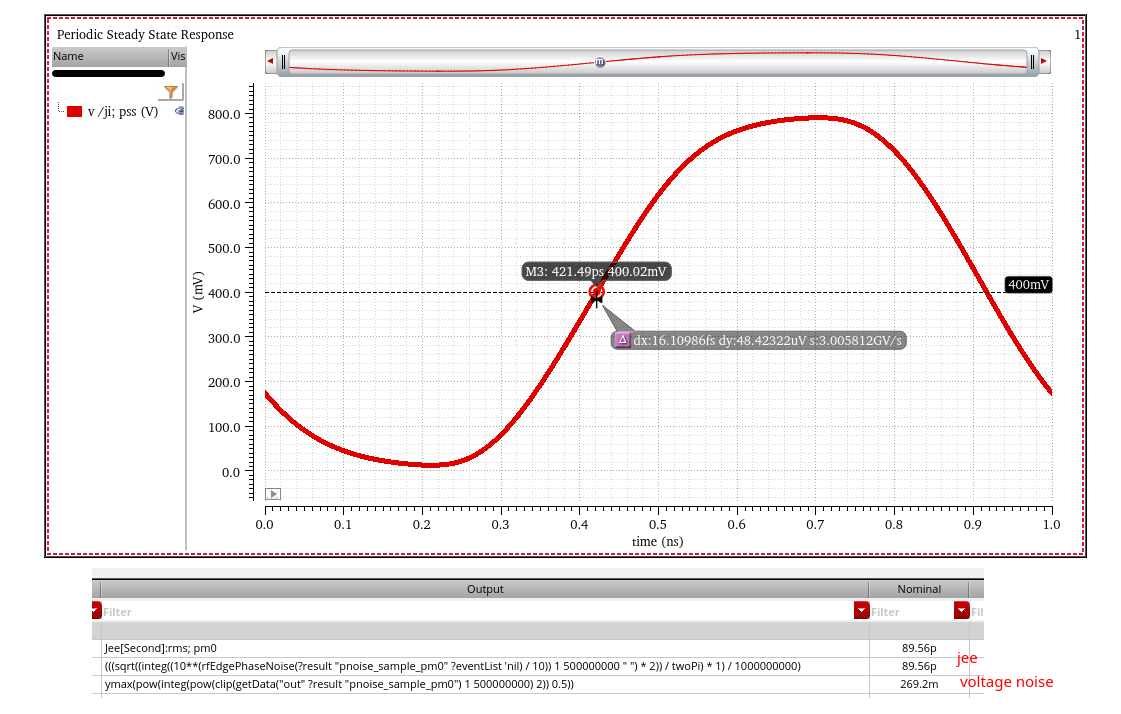
By PSS_Pnoise

jee

1

rfEdgePhaseNoise(?result "pnoise_sample_pm0" ?eventList 'nil) + 10 * log10(2)

convert single-sideband phase noise to psd by multiplying 2 or 10 * log10(2)

By trannoise PN function

1

PN(clip(VT("/Out1") 2.60417e-08 0.000400052) "rising" 1.65 ?Tnom (1 / 3.84e+07) ?windowName "Rectangular" ?smooth 1 ?windowSize 15000 ?detrending "None" ?cohGain 1 ?methodType "absJitter")

double-sideband psd

By trannoise psd and abs_jitter function

1

dB10(psd(abs_jitter(clip(VT("/Out1") 2.60417e-08 0.000400052) "rising" 1.65 ?Tnom (1 / 3.84e+07)) 2.60417e-08 0.000400052 15360 ?windowName "Rectangular" ?smooth 1 ?windowSize 15000 ?detrending "None" ?cohGain 1))

double-sideband psd

abs_jitter Y-Unit default is rad

Comparison

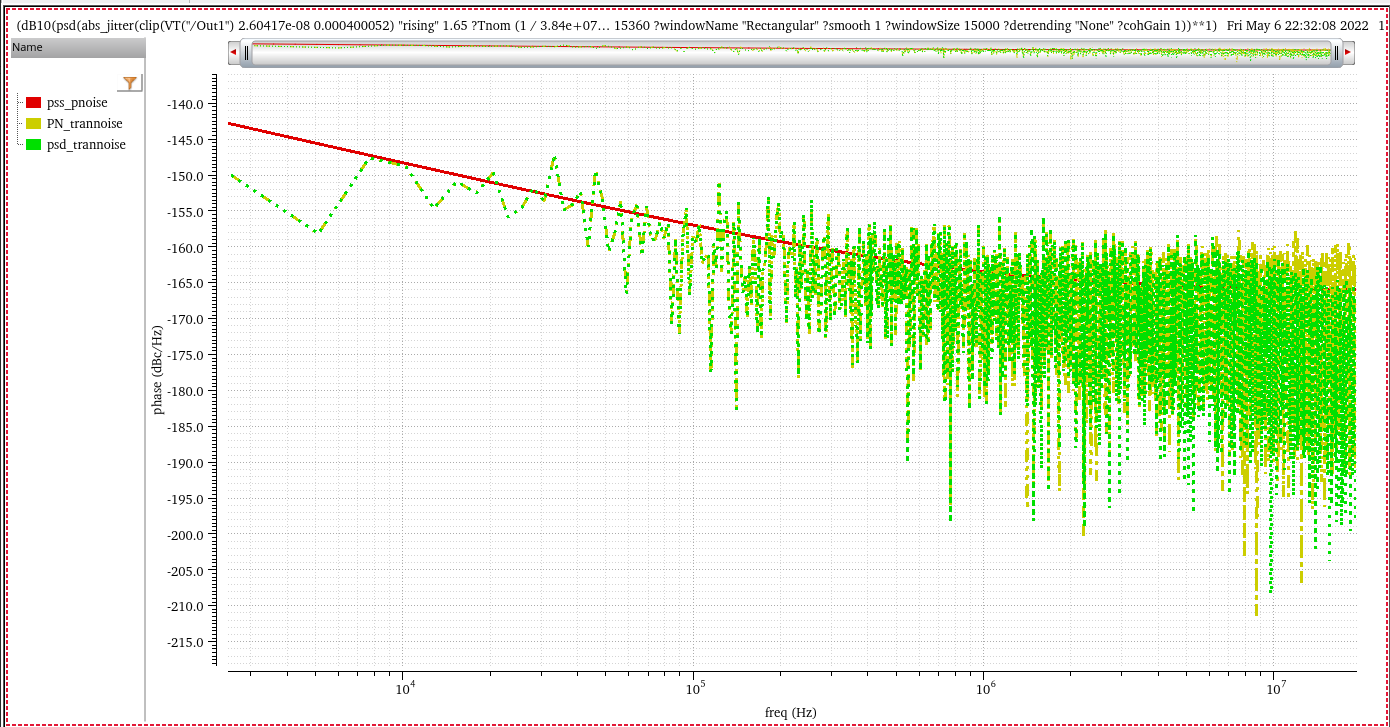
PN's result is same with psd's

RMS value

• build the abs_jitter function with seconds as the Y axis and add the stddev function to determine the Jee jitter value
• or integrate psd

The RMS \(x_{\text{RMS}}\) of a discrete domain signal \(x(n)\) is given by \[ x_{\text{RMS}}=\sqrt{\frac{1}{N}\sum_{n=0}^{N-1}|x(n)|^2} \] Inserting Parseval's theorem given by \[ \sum_{n=0}^{N-1}|x(n)|^2=\frac{1}{N}\sum_{n=0}^{N-1}|X(k)|^2 \] allows for computing the RMS from the spectrum \(X(k)\) as \[ x_{\text{RMS}}=\sqrt{\frac{1}{N^2}\sum_{n=0}^{N-1}|X(k)|^2} \]

Cadence Spectre's PN function may call abs_jitter and psd function under the hood.

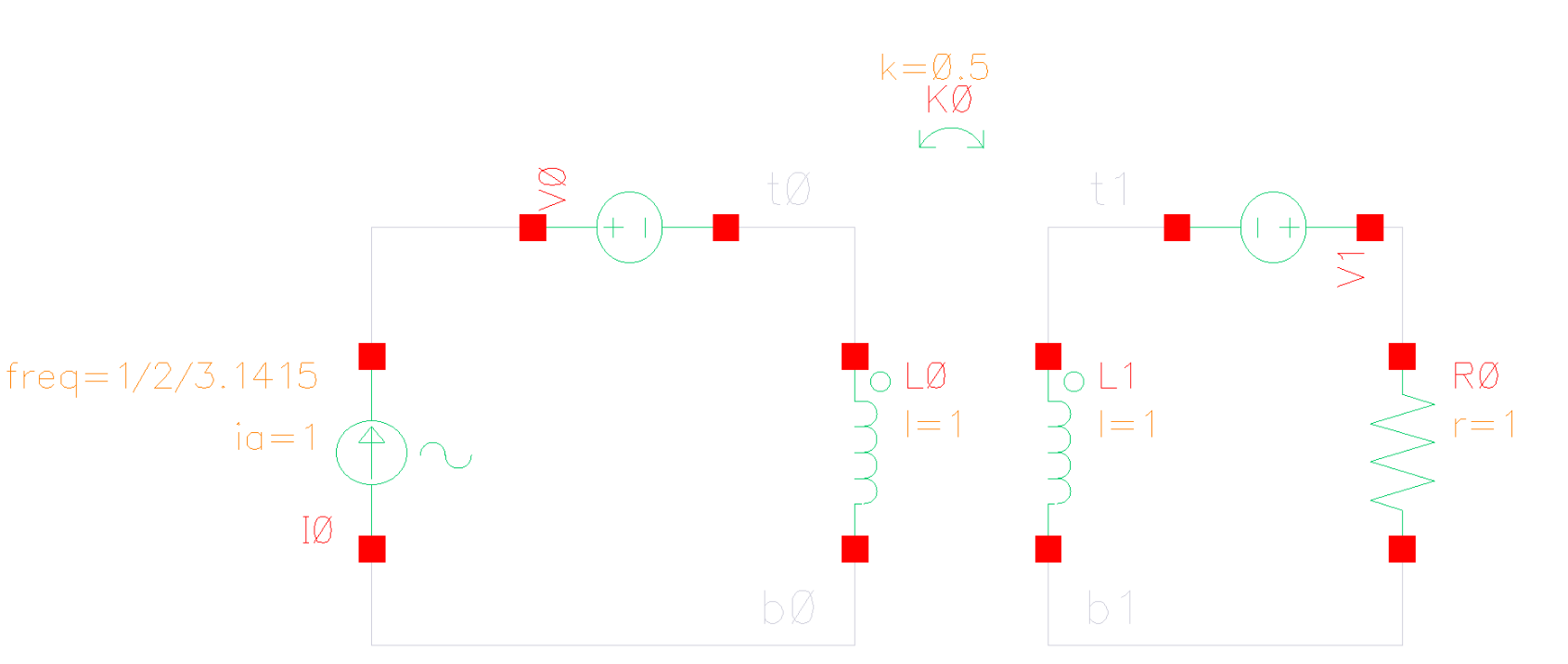
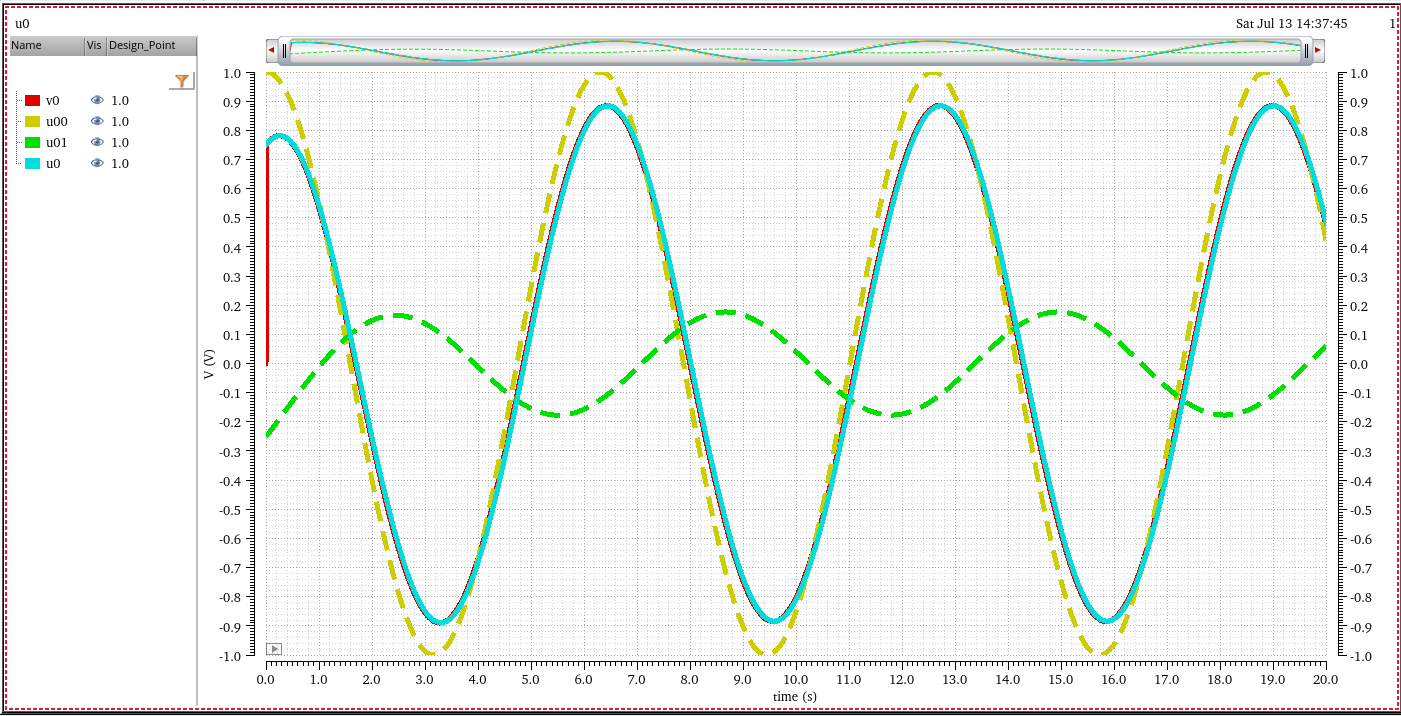
Phase Noise in vsource

Article 20256770 How to specify phase noise as an instance parameter in spectre sources (e.g. vsource, isource, port) [https://community.cadence.com/cadence_blogs_8/b/rf/posts/how-to-specify-phase-noise-as-an-instance-parameter-in-spectre-sources-e-g-vsource-isource-port]

Suppose pnoise result of one block is shown as below, and the result is stimulus of following block

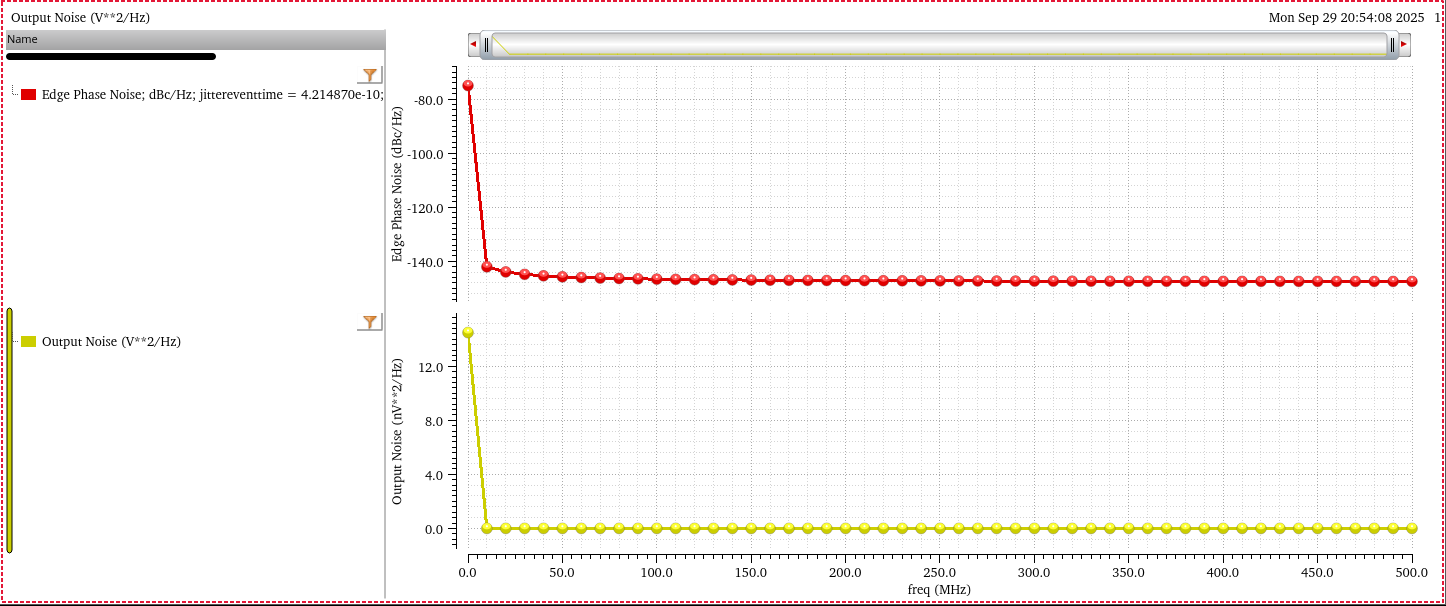
First export Output Noise and Edge Phase Noise， then select noiseModelType and noisefile respectively

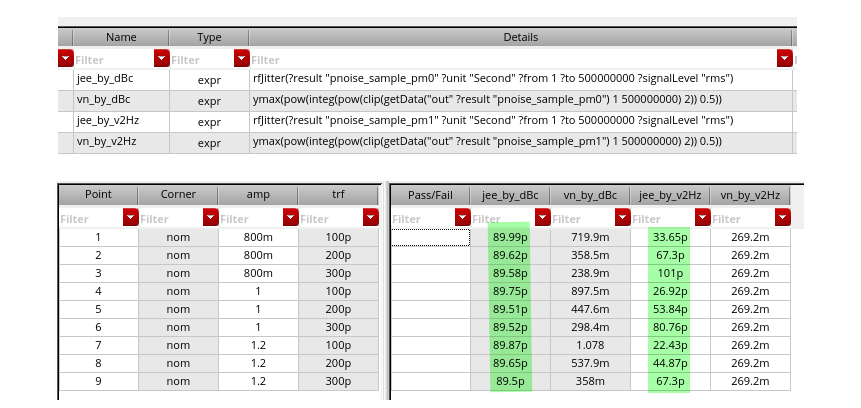
Under vsource (Source type: pulse) with different amplitude & rising/falling time, simulation result demonstrate that Edge Phase Noise(dBc) maintain jitter or phase noise by tweaking voltage noise at edge under the hoods, however Noise Voltage(V^2/Hz) maintain voltage noise

In the conclusion, Edge Phase Noise(dBc) is preferred for phase noise evaluation

notice:

@(#)$CDS: spectre version 21.1.0 64bit 12/01/2023 07:24 (csvcm36c-1) $

@(#)$CDS: virtuoso version ICADVM20.1-64b 10/11/2023 09:26 (cpgbld01) $

SSB Phase Noise (dBc)

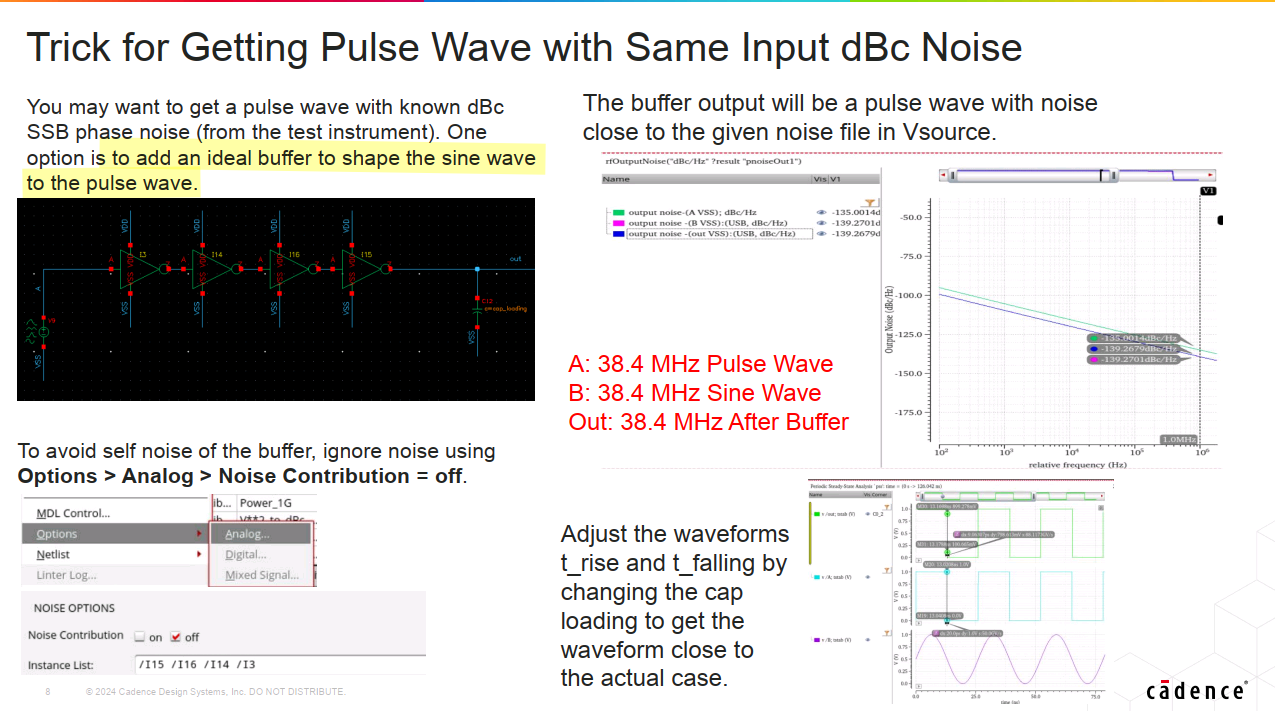
Divider PN simulation

Cadence Support. "How to set up pss/pnoise when simulating a driven circuit or a VCO, both containing dividers"

reference

Article (11514536) Title: How to obtain a phase noise plot from a transient noise analysis

Article (20500632) Title: How to simulate Random and Deterministic Jitters

Cadence, Application Note: Understanding the relations between time-average noise (phase-noise) and sampled noise (edge-phase noise or jitter) in Pnoise analysis

Jens Ahrens, Carl Andersson, Patrik Höstmad, Wolfgang Kropp. Tutorial on Scaling of the Discrete Fourier Transform and the Implied Physical Units of the Spectra of Time-Discrete SignalsURL: https://appliedacousticschalmers.github.io/scaling-of-the-dft/AES2020_eBrief/

Load-Transient Response

TODO 📅

bleeding current

A bleeding resistor (or a dedicated bleeding current source) is typically used in a Low Dropout (LDO) voltage regulator or a power supply circuit to ensure stability and proper operation under light load or no-load conditions [Google AI Mode]

resistor: affect both DC and AC (small signal)

current source: affect DC bias only (assuming infinite output impedance of current source)

Kelvin connection

Kelvin connection in IC design [https://analoghub.ie/category/Circuits/article/kelvinConnection]

The entire idea behind Kelvin connection is to separate the nodes that are carrying high currents from the sensing nodes to the feedback

Error Amplifier

Using type B amplifier to drive the NMOS power stage will enhance the NMOS’s PSRR performance

PSRR (Power Supply Rejection Ratio)

A good PSRR is important when an LDO is used as a sub-regulator in cascade with a switching regulator

The LDO would need to have a sufficiently high rejection at the switching frequency of the switching converter to filter out the ripples at that frequency

Mid-Frequency PSRR

High frequency PSRR

Open-Loop PSRR

Chen, Feng & Lu, Yasu & Mok, Philip. (2022). Transfer Function Analysis of the Power Supply Rejection Ratio of Low-Dropout Regulators and the Feed-Forward Ripple Cancellation Scheme. IEEE Transactions on Circuits and Systems I: Regular Papers. [https://sci-hub.se/10.1109/TCSI.2022.3167860]

Yan Lu, HW #3 - "Precision Low-Dropout Regulators" Online Course (2025) [https://youtu.be/LXX1Xuhv2kI]

neglect the contribution of the voltage regulation circuits to the PSRR

HW #3 - "Precision Low-Dropout Regulators" Online Course (2025) - Prof. Yan Lu (Tsinghua University) [https://youtu.be/LXX1Xuhv2kI]

In a PMOS LDO, we want the gate of the power MOS transistor to track the power supply ripple. This keeps the \(V_{GS}\) relatively constant, which in turn ensures a stable supply of current through the transistor

DC output impedance

The output impedance of the LDO at DC is known as its load regulation

DC output impedance of NMOS and PMOS LDO is the same for the same error amplifier gain

\[ R_{\text{out}} = \frac{1}{\beta A_{o1} g_{m2}} \]

The NMOS LDO has a faster response to line transients than the PMOS LDO since it has better (smaller) PSRR

Power MOS gain affect on PMOS LDO

DC gain \[ A_{dc} = g_mR_\text{ota} A_2 \] 3dB bandwidth \[ \omega_p = \frac{1}{R_\text{ota}(C_g+A_2C_c)} \] and GBW \[ \omega_u = \frac{g_m}{\frac{C_g}{A_2}+C_c} \]

Feedforward Compensation with \(C_\text{FF}\)

• Improved Noise
• Improved Stability and Transient Response
• Improved PSRR

\[\begin{align} R_1 \parallel \frac{1}{sC_{FF}} &= \frac{R_1}{1+sR_1C_{FF}} \\ Z_o &= \left( R_1\parallel \frac{1}{sC_{FF}}+R_2\right)\parallel \frac{1}{sC_L} \\ &=\frac{R_1+R_2+sR_1R_2C_{FF}}{s^2R_1R_2C_{FF}C_L + s[(R_1+R_2)C_L+R_1C_{FF}]+1} \\ A_{V2} &= g_m Z_o \\ &= g_m \frac{R_1+R_2+sR_1R_2C_{FF}}{s^2R_1R_2C_{FF}C_L + s[(R_1+R_2)C_L+R_1C_{FF}]+1} \\ \beta &= \frac{R_2}{\frac{R_1}{1+sR_1C_{FF}}+R_2} \\ &= \frac{R_2(1+sR_1C_{FF})}{R_1+R_2+sR_1R_2C_{FF}} \\ A_{V2}\beta &= \frac{g_mR_2(1+sR_1C_{FF})}{s^2R_1R_2C_{FF}C_L+s[(R_1+R_2)C_L+R_1C_{FF}]+1} \end{align}\]

That is, adding a \(C_{FF}\) also introduces a zero (\(\omega_z\)) and pole (\(\omega_p\)) into the LDO feedback loop

\[\begin{align} \omega_{po} &= \frac{1}{(R_1+R_2)C_L} \\ \omega_z &= \frac{1}{R_1C_{FF}} \\ \omega_{p} &= \frac{1}{(R_1 \parallel R_2)C_{FF}} \end{align}\]

Application Report SBVA042–July 2014, Pros and Cons of Using a Feedforward Capacitor with a Low-Dropout Regulator [https://www.ti.com/lit/an/sbva042/sbva042.pdf]

LDO Basics: Noise – How a Feed-forward Capacitor Improves System Performance [https://www.ti.com/document-viewer/lit/html/SSZTA13]

LDO Basics: Noise – How a Noise-reduction Pin Improves System Performance [https://www.ti.com/document-viewer/lit/html/SSZTA40]

NMOS Slave LDO

\[\begin{align} \frac{V_g}{V_i} &=\frac{R||\frac{1}{s(C_g+C_{gs})}}{R||\frac{1}{s(C_g+C_{gs})}+\frac{1}{sC_{gd}}} \\ &= \frac{sRC_{gd}}{sR(C+C_{gd}+C_{gs})+1} \\ \frac{V_g}{V_i} &= -\frac{sC_{ds}+g_{ds}}{sC_{gs}+g_m} \end{align}\]

That is, \[ \omega_{z,d} \approx \frac{1}{R(\frac{g_m}{g_{ds}}C_{gd}+C)} \]

To calculate PSRR pole is similar with above PSRR zero, though \(V_o/V_i=0\), i.e. set \(V_0\) 0 potential \[ \omega_{p,d} \approx \frac{1}{R(\frac{C_s}{g_mR}+C)} \]

DC PSRR \[ \text{PSRR} = \frac{1}{g_mr_o} \]

PSRR @Vgate

KCL at output node

\[ g_m(-V_o\beta A_{E} - V_o) + \frac{V_i - V_o}{r_o} = \frac{V_o}{R_1+R_2} \]

Hence \[ \frac{V_o}{V_i} = \frac{1}{A_E\beta g_mr_o+g_mr_o +\frac{r_o}{R_1+R_2}+1} \approx \frac{1}{A_E\beta g_m r_o} \]

Through feedback loop, we derive \[ V_g = V_o \beta (-A_E) \approx \frac{V_i}{A_E\beta g_m r_o} \beta (-A_E) = -\frac{V_i}{g_mr_o} \]

That is \[ \frac{V_g}{V_i} \approx -\frac{1}{g_mr_o} \]

Due to closed loop, \(V_g\) and \(V_o\) is not source follower

NMOS LDO

For ESD considertion, NMOS is placed in DNW, which provide ESD discharging path from source to AVDD

feedback resistor divider noise

assuming \(\text{LG} \gg 1\)

\[\begin{align} I_\text{t} &= \frac{V_\text{ref} - v_\text{n2}}{R_\text{2}} \\ V_\text{o} &= V_\text{ref} +v_\text{n1} + I_\text{t}R_\text{1} \\ \end{align}\]

Then \[ V_\text{o} = \frac{R_1+R_2}{R_2}V_\text{ref} + v_\text{n1} - \frac{R_1}{R_2}v_\text{n2} \] that is

\[ v_\text{no}^2 = v_\text{n1}^2 + \left(\frac{R_1}{R_2}\right)^2 v_\text{n2}^2 \]

\[ \text{vno1}^2= \text{vn1}^2+\text{vn2}^2/6^2=16.5758 + 99.45453/6^2 = 19.338425833 \]

stability vs feedback ratio

Since loop gain \(\text{LG} = A\beta\), stability degrades as the feedback ratio \(\beta\) increases.

Therefore, at a fixed \(V_{ref,in}\), the lowest output voltage (\(\beta=1\)) represents the canonical worst-case scenario for stability

reference

Hinojo, J.M., Martinez, C.I., & Torralba, A.J. (2018). Internally Compensated LDO Regulators for Modern System-on-Chip Design.

Chen, K.-H. (2016). Power Management Techniques for Integrated Circuit Design. Wiley-IEEE Press.

Morita, B.G. (2014). Understand Low-Dropout Regulator ( LDO ) Concepts to Achieve Optimal Designs.

H. -S. Kim, "Exploring Ways to Minimize Dropout Voltage for Energy-Efficient Low-Dropout Regulators: Viable approaches that preserve performance," in IEEE Solid-State Circuits Magazine, vol. 15, no. 2, pp. 59-68, Spring 2023, doi: 10.1109/MSSC.2023.3262767.

—, "Fundamentals of Energy-Efficient LDO Regulator Design: From dropout optimization to wide-bandwidth and high-PSR techniques," in IEEE Solid-State Circuits Magazine, vol. 18, no. 3, pp. 55-72, Summer 2026, doi: 10.1109/MSSC.2026.3696588

Ali Sheikholeslami, Circuit Intuitions: Voltage Regulators IEEE Solid-State Circuits Magazine, Vol. 12, Issue 4, to appear, Fall 2020.

Operational Transconductance Amplifier II Multi-Stage Designs [https://people.eecs.berkeley.edu/~boser/courses/240B/lectures/M07%20OTA%20II.pdf]

Toshiba, Load Transient Response of LDO and Methods to Improve it Application Note [https://toshiba.semicon-storage.com/info/application_note_en_20210326_AKX00312.pdf?did=66268]

Carusone, Tony Chan, David Johns, and Kenneth Martin. Analog integrated circuit design. John wiley & sons, 2011. [https://mrce.in/ebooks/Analog%20Integrated%20Circuit%20Design%202nd%20Ed.pdf]

Pavan Kumar Hanumolu. CICC 2015. "Low Dropout Regulators" [https://uofi.app.box.com/v/CICC15-LDO]

Mingoo Seok. ISSCC 2020 T7: "Basics of Digital Low-Dropout (LDO) Integrated Voltage Regulator"

Yan Lu, ISSCC2021 T10: "Fundamentals of Fully Integrated Voltage Regulators"

—, (Tsinghua U.) Preview - “Precision Low-Dropout Regulators” Online Course (2025) [https://youtu.be/IgWTou7Ikbs]

Mao, Xiangyu, Yan Lu, and Rui P. Martins. Fully-Integrated Low-Dropout Regulators. Springer, 2025.

Hyun-Sik Kim, Low-Dropout (LDO) Voltage Regulators – From Basics to Recent Design Trends (presented in A-SSCC 2022) [pdf]

A. Raychowdhury. ISSCC 2024 T2: Fundamentals of Digital and Digitally-Assisted Linear Voltage Regulators

Mixed-Mode S-parameter

12 May 2021 Introduction to Mixed-Mode S-parameters [https://blog.teledynelecroy.com/2021/05/introduction-to-mixed-mode-s-parameters.html]

Troy Beukema (IBM Research, Yorktown Heights, NY). 03-Sep-2009. Topics in Design and Analysis of High Data Rate SERDES Systems [https://ewh.ieee.org/r5/denver/sscs/Presentations/2009_09_Beukema.pdf]

Bert Simonovich. A Guide for Single-Ended to Mixed-Mode S-parameter Conversions [https://www.signalintegrityjournal.com/articles/1832-a-guide-for-singleended-to-mixedmode-s-parameter-conversions]

single-ended S-parameters

Mixed-mode S-parameters

Missing Term in KVL

Prof. Kolb/Whites. EE 382 Applied Electromagnetics Lecture 8: Maxwell's Equations and Electrical CIrcuits [http://montoya.sdsmt.edu/ee382/lectures/382Lecture8.pdf]

Transmission-line

Telegrapher's equations

EECS 723- Microwave Engineering Spring 2.1 -The Lumped Element Circuit Model for Transmission Lines

1/20/2005 [https://www.ittc.ku.edu/~jstiles/723/handouts/2_1_Lumped_Element_Circuit_Model_package.pdf]

note [https://www.ittc.ku.edu/~jstiles/723/handouts/section_2_1_The_Lumped_Element_Circuit_Model_package.pdf]

present [https://www.ittc.ku.edu/~jstiles/723/handouts/section_2_1_The_Lumped_Element_Circuit_Model_present.pdf]

Transmission Line Wave Equation

Characteristic Impedance (\(Z_0\))

Remember, S-parameters don't mean much unless you know the value of the reference impedance (it's frequently called Z0).

simulator will read sp file's Z0 parameter

The default Z0 exported by EMX is 50

Complex Propagation Constant \(\gamma\)

TODO 📅

Input impedance (Line Impedance)

Reflection Coefficient

TODO 📅

Steady-State Solution (DC voltage division)

Sam Palermo. [https://people.engr.tamu.edu/spalermo/ecen689/lecture3_ee689_tlines.pdf]

Kyoung-Jae Chung. Special Topics in Radiation Engineering (High-voltage pulsed power engineering) [https://ocw.snu.ac.kr/sites/default/files/NOTE/Lecture_03_Transmission%20line%20theory.pdf]

David R. Jackson. [https://courses.egr.uh.edu/ECE/ECE3317/SectionJackson/Class%20Notes/Notes%208%203317%20Transmission%20Lines%20(Bounce%20Diagram).pdf]

Shouri Chatterjee [https://web.iitd.ac.in/~shouri/ell112/material/txline.pdf]

How can I go from transmission line model to lumped elements model? [https://physics.stackexchange.com/a/386603]

E157 Introduction to Radio Frequency Circuit Design [https://pages.hmc.edu/mspencer/e157/fa24/]

Shen Lin. On-Chip Inductance and Coupling Effects [http://eda.ee.ucla.edu/pub/asic.pdf]

A. Deutsch et al., "When are transmission-line effects important for on-chip interconnections?," in IEEE Transactions on Microwave Theory and Techniques, vol. 45, no. 10, pp. 1836-1846, Oct. 1997

Ho, Ron. “Chip Wires: Scaling and Efficiency.” (2003). [https://www-vlsi.stanford.edu/people/alum/pdf/0303_Ho_Wires.pdf]

—. ISSCC 2007 T3: Dealing with Issues in VLSI Interconnect Scaling, by Ron Ho

Tony Chan Carusone. ISSCC 2017 T6: Signal Integrity Analysis for Gb/s Links

Byungsub Kim ISSCC 2022 T11: "Basics of Equalization Techniques: Channels, Equalization, and Circuits"

Power Wave Equations

Peter J. Pupalaikis (Ciena). DesignCon 2026: Port Referencing in S-Parameters – Critical Insights You Need to Know

1
2
3
4
5
6
7
8
9
10
11
12
13

Transmission Line Theory
        │
        ▼
v = v⁺ + v⁻,  i = (v⁺ - v⁻)/Z0      ← Physical decomposition
        │
        ▼
v⁺ = (v + iZ0)/2,  v⁻ = (v - iZ0)/2   ← Solve for forward/backward waves
        │
        ▼
a = v⁺/√Z0,  b = v⁻/√Z0               ← Normalize so |a|² = power
        │
        ▼
v = √Z0·(a+b),  i = (a-b)/√Z0          ← Invert to recover v and i

Z0 is a chosen reference impedance (typically 50Ω), which is an arbitrary normalization choice. It does not have to equal the characteristic impedance of the transmission line

Voltage scattering

transmitted voltage \[ V= \frac{2Z_l}{Z_l+R_0}\frac{V_s}{2}= \frac{Z_l}{Z_l+R_0}\cdot V_s \]

CHAPTER 6 Transmission-Line Essentials for Digital Electronics [https://ws.engr.illinois.edu/sitemanager/getfile.asp?id=178]

CHAPTER 7 Transmission-Line Analysis [https://ws.engr.illinois.edu/sitemanager/getfile.asp?id=199]

Voltage Transfer Function

Troy Beukema (IBM Research, Yorktown Heights, NY). 03-Sep-2009. Topics in Design and Analysis of High Data Rate SERDES Systems [https://ewh.ieee.org/r5/denver/sscs/Presentations/2009_09_Beukema.pdf]

Pupalaikis, Peter. (2012). The Relationship Between Discrete-Frequency S-parameters and Continuous-Frequency Responses. [pdf]

Impulse Response from S-Parameters (channel)

David Banas. A comparison of different techniques (i.e. - windowing, vector fitting, etc.) for extracting the impulse response from S-parameters. [https://github.com/capn-freako/ImpulseResponseFromSparameters/tree/main]

—, Impulse Response from Insertion Loss [https://www.signalintegrityjournal.com/articles/1847-impulse-response-from-insertion-loss]

Sam Palermo. ECEN720: High-Speed Links Circuits and Systems Spring 2025 - Lecture 3: Time-Domain Reflectometry & S-Parameter Channel Models [https://people.engr.tamu.edu/spalermo/ecen689/lecture3_ee720_tdr_spar.pdf]

Troy Beukema (IBM Research, Yorktown Heights, NY). 03-Sep-2009. Topics in Design and Analysis of High Data Rate SERDES Systems [https://ewh.ieee.org/r5/denver/sscs/Presentations/2009_09_Beukema.pdf]

Cadence application note: 7 Habits of Highly Successful S-Parameters, Spectre 21.1

Derek Rowell, 2.161 Signal Processing: Continuous and Discrete Fall 2008: Determining a System’s Causality from its Frequency Response [https://ocw.mit.edu/courses/2-161-signal-processing-continuous-and-discrete-fall-2008/142cd928b3b3959721198872ab97b647_causality.pdf]

Causality

Kramers–Kronig / Hilbert-transform causality relation — Magnitude/real part and phase/imaginary part cannot be chosen independently. \[ \boxed{H_I(\omega) = -\mathcal{H}\{H_R(\omega)\}} \qquad \boxed{H_R(\omega) = \mathcal{H}\{H_I(\omega)\}} \] where \(H_R(\omega) = \operatorname{Re}\{H(\omega)\}\) and \(H_I(\omega) = \operatorname{Im}\{H(\omega)\}\)

Conjugate symmetry only ensures the time-domain signal is real

Hz-domain formula

angular frequency formula

single pole low pass filter

Passivity

causality-passivity correction

P. Triverio, S. Grivet-Talocia, M. S. Nakhla, F. G. Canavero and R. Achar, "Stability, Causality, and Passivity in Electrical Interconnect Models," in IEEE Transactions on Advanced Packaging, vol. 30, no. 4, pp. 795-808, Nov. 2007 [https://sci-hub.ru/10.1109/TADVP.2007.901567]

S. Sercu, C. Kocuba, J. Nadolny, "Causality Demystified", in DesignCon 2015, Jan. 2015 [pdf]

Vinod Arjun Huddar. Causality Problems in Power Delivery Networks [https://www.signalintegrityjournal.com/articles/1217-causality-in-power-delivery-network-in-package-board]

Tyler Huddleston, Signal Edge Solutions. Causality in Practice: How Frequency Sampling and Bandwidth Shape Time-Domain Fidelity [https://www.signalintegrityjournal.com/articles/4061-causality-in-practice-how-frequency-sampling-and-bandwidth-shape-time-domain-fidelity]

Interpolation Methods

jinghua Huang SYNOPSYS. Optimum Frequency Sampling in S-Parameter Extraction and Simulation [https://ibis.org/summits/nov08a/huang.pdf]

• convolution-based method (ifft): linear, spline

• rational approximation method: bbspice, rational

Broadband SPICE (bbspice) – a Rational Interpolation Method

Real/Imaginary(RI) Magnitude/Angle(MA) interpolation

Rational Fit

Use the rational function to fit data defined in the frequency domain with an equivalent Laplace transfer function. Using rational function fitting you can create simple models for a required accuracy, model order reduction, zero phase on extrapolation to DC, and causal modeling system among other advantages

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

filename  = 'touchstone/ISI.S4P';
s4p = read(rfdata.data, filename);
sdd_params = s2sdd(s2p.S_Parameters, 2);
sdd21 = squeeze(sdd_params(2, 1, :));   % s21
freq = s4p.Freq;

% rational fitting
weight = ones(size(sdd21));
weight(floor(end*3/4):end) = 0.2;
weight(2:10) = 0;

[hfit, errb] = rationalfit(freq, sdd21, 'IterationLimit', [4, 16], 'Delayfactor', 0.98, ...
    'Weight', weight, 'Tolerance', -38, 'NPoles', 32);
[sdd21_fit, ff] = freqresp(hfit, freq);

figure(1)
plot(freq/1e9, db(sdd21), 'b-'); hold on;
plot(ff/1e9, db(sdd21_fit), 'r-'); hold off; grid on;
legend('sdd21', 'sdd21\_fit');
xlabel('Freq (GHz)');
ylabel('magnitude (dB)');


ts = 1e-12;
n = 2^18;
trise = 4e-14;
[yout, tout] = stepresp(hfit, ts, n, trise);
figure(2)
plot(tout*1e12, yout, 'b-'); grid on;
xlabel('Time (ps)');
ylabel('V');
title('Step Response');


% write verilog-A
writeva(hfit, 'channel_32poles.va');

Cascading S-Parameters

Sam Palermo, Lecture 6: S-Parameter Channel Examples [https://people.engr.tamu.edu/spalermo/ecen689/lecture6_ee689_sparam_channels.pdf]

Cascading S-Parameters in Plain English: Part 3: T-Parameters in Plain English [http://thinkinitthrough.com/blogs/details/6]